基于勒贝格采样的非线性系统优化控制
2019-07-11朱萌萌宋运忠
朱萌萌,宋运忠
(河南理工大学电气工程与自动化学院,河南 焦作 454000)
0 引言
随机系统广泛存在于实际的生产生活中,比如,在社会经济、航天航空、生物医学、生态环境、工业过程等领域,许多系统会受到外界随机干扰和观测噪声的影响形成非线性随机扰动,造成系统的性能差、不稳定。类似这些内部含有随机变量,外部受随机扰动或噪声干扰的系统,称为随机系统[1-7]。为了改善系统的性能,降低外界干扰的影响,专家们开始利用随机的观点分析和解决此类实际问题。从而推动了随机系统优化控制理论的迅速发展,也使其成为目前最优控制领域的重要研究方向之一。
近年来,随机系统的最优控制理论已逐步完善和成熟。但是,大部分研究成果的取得均依赖于系统精确地数学模型,这对于实际系统来说是复杂的,分析起来极其困难。因而,把连续信号转换成离散信号的采样过程,是求解随机系统控制问题的一种行之有效的方法。采样定理的提出已有70多年,学者们相继提出了多种采样方法,并利用这些采样方案解决不同的控制问题[8-10]。其中,周期采样和事件触发采样机制是解决此类控制问题的两种常用方法。传统的采样方法是周期性采样,无论系统状态如何变化,采样间隔往往是不变的。虽然,这种采样策略的问题比较容易研究,但是也容易造成计算资源和通信资源的浪费,在某种程度上也易造成“维数灾”。因此,可变采样速率的采样方案得到了研究者的广泛关注。这种采样方法的特点是只有当满足系统状态的变化量超过事先给定的阈值后,系统状态的信息才被采样并实施控制。这种采样机制被称为勒贝格采样,又叫事件触发采样。勒贝格采样方法早在20世纪60年代就被提出,在实际系统中的应用亦得到了广泛研究。譬如,文献[11]基于脉冲系统、分段线性系统和扰动线性系统分别提出了3种方法来分析事件触发控制系统的稳定性,理论上研究了线性系统的周期事件驱动控制。文献[12]在减少目标跟踪系统通信量的同时保证系统的最优估计性能,针对目标跟踪问题,将事件驱动控制扩展到了非线性系统中。文献[13]针对线性系统状态反馈控制问题,利用脉冲控制方法,研究了事件触发控制系统的稳定性。文献[14]针对连续时间非线性系统的控制问题,设计了最优自适应事件触发控制算法。文献[15]针对积分器的稳定性问题,在勒贝格采样环境下提出了一种非线性控制律,从而使系统达到渐近稳定。基于上述文献,学者们在很大程度上对事件触发机制的应用研究做出了杰出贡献,使最优控制理论得到了进一步的完善。但是,在这些文献中,采用事件触发采样时的控制策略往往简单,如脉冲控制、开关控制、启发式PID控制或自适应触发控制,并且大部分针对的是连续时间线性系统或者离散时间非线性系统。然而,基于勒贝格采样的连续非线性系统的最优控制问题还没有一个完整的模型,也没有得到深入的研究。因此,本文提出了基于勒贝格采样的非线性系统最优控制模型,并给出了基于马尔可夫决策过程的求解方法。
本文主要研究了连续时间非线性系统的最优控制问题,提出了基于勒贝格采样的一般最优控制方案。首先,给出了勒贝格采样系统模型的数学描述。然后,利用马尔可夫决策过程中的时间集结方法搭建模型,并通过策略迭代算法对该模型进行Matlab仿真,结合解析法求解策略迭代算法中系统的相关参数。最后,利用仿真算例,通过给定初始策略求得勒贝格采样系统的最优策略和平均采样间隔,再用此平均采样间隔作为周期性采样系统的等采样间隔,对比两种采样策略,可以发现基于勒贝格采样的非线性系统的优化性能好于基于周期采样的随机动态系统。为了更好地说明方法的有效性,分别定量地改变代价函数的控制能量和事件的状态值对其进行仿真研究,实验结果再次表明勒贝格采样系统不仅改善了系统性能,还减小了系统能耗。
1 问题描述
给定一个1维连续非线性控制系统[16]:
dx=μ(x,u)dt+σdv
(1)
其中,x=x(t)∈R表示系统在t时刻的状态,u=u(t)∈U⊂Rn为系统在t时刻的控制量,U是控制量的集合,v=v(t)表示一个维纳过程,σ是常数。μ(x,u)为“状态-行动”对的数值函数。假设系统(1)是勒贝格可测函数,则系统的代价函数记为fu(x)。研究随机系统的最优控制问题,其目的就是找一个最优控制律u(t),t∈[0,∞),使无穷时段长期平均性能最小。
定义系统的无穷时段长期平均性能为
(2)
其中,“E”表示概率测度下的期望,假设在控制变量u(t)的作用下系统是稳定的,那么上述性能ηu与初始状态x(0)无关。
2 基于勒贝格采样系统的最优控制
2.1 勒贝格采样系统
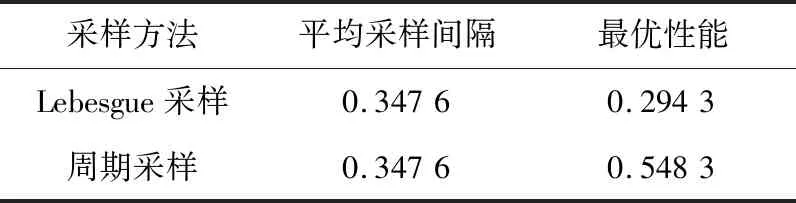
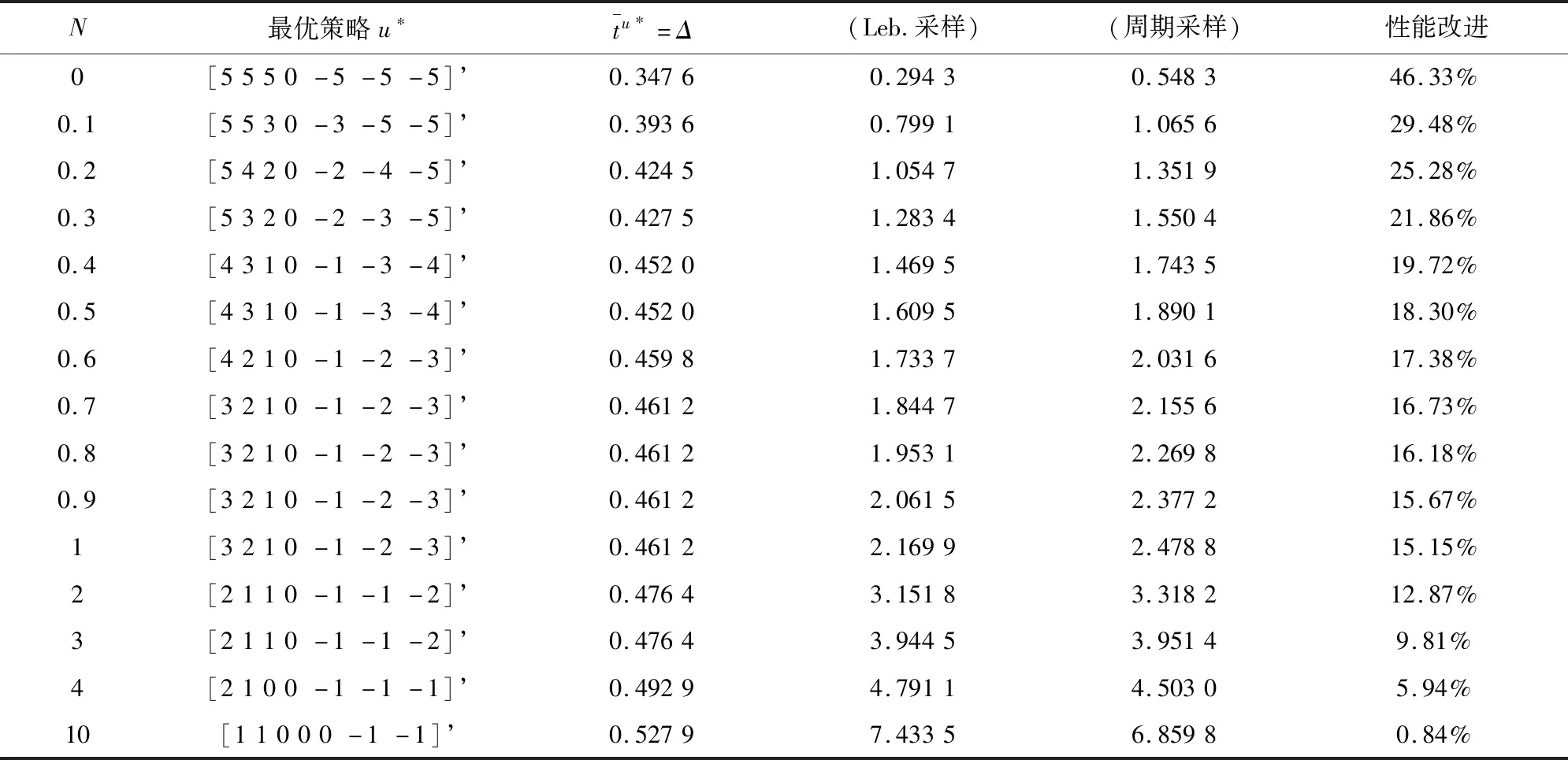
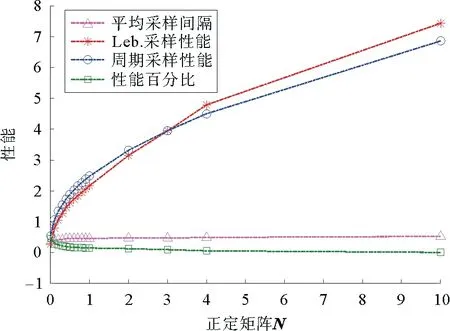
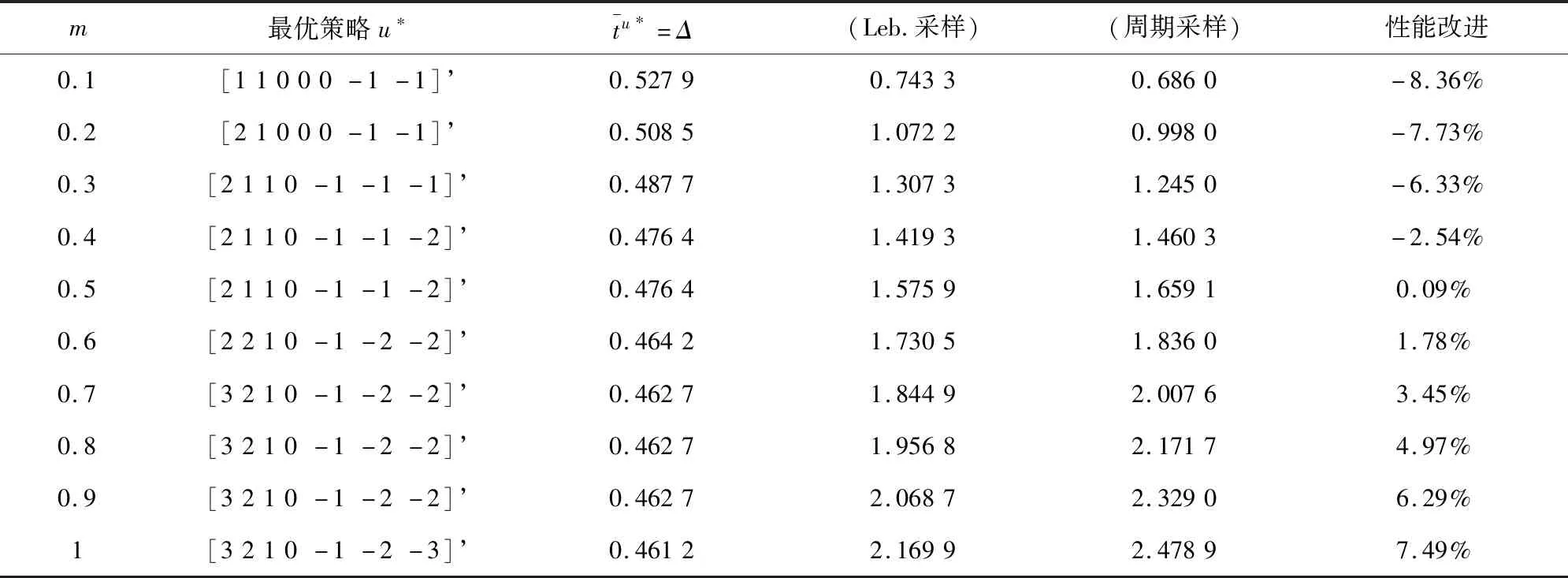
本文研究的勒贝格采样[17-18]定义如下:首先,定义一个有限离散事件集合:D={1,…,D} 。每一个事件d∈D对应系统的一个状态值xd。那么,事件集合D相对应的系统状态值的集合为χD={xd:d∈D}⊂R,简称事件的值集合。为了更加完整地描述系统的一般数学模型,假设x1 ti= min{t:t>ti-1,x(t)∈χD,x(t)≠x(ti-1)} (3) 对所有的i=1,2,…均成立。发生在时刻ti的事件记做di∈D,则{di,i=0,1,2,L}构成了一个嵌入链。为了保证嵌入链是发生在离散时刻,即di+1-di∈{-1,1},从而排除了di+1=di的情况。如上所述,只在事件发生的时候才进行的采样过程,被称为勒贝格采样。 勒贝格采样又称基于事件的采样,由此可结合基于事件驱动的优化控制方法来研究系统模型。在基于勒贝格采样的系统模型构建中,系统的控制量是在系统状态被采样的时候加入的,直到下一个采样时刻发生才停止。因此,在时刻ti的控制量,记做ui。数学符号描述为:u(t)=ui且t∈[ti,ti+1)。原动态系统(1)可以描述为 dx=μ(xi,ui)dt+σdv,ti≤t (4) 其中,ui表示系统在时刻ti所加入的控制量,又称为事件的行动。它是由控制策略所决定的,记为ui=u(di),di∈D,ui∈U,i= 0,1,L。这个与事件di有关的控制策略称为控制律或策略,记作u。从式(4)可得,行动ui仅由事件di决定,因此u称作基于事件的策略。假设可采取的行动集合U是有限的,则原系统(1)的问题就变成了如何选择一个最优控制策略u使得动态系统(4)的平均性能最小。 研究动态系统的最优控制问题常常通过搭建马尔可夫数学模型来求解,许多关于马尔可夫模型的优化设计方法也均可适用。因此,可以通过构造一个等价的马尔可夫模型,再结合时间集结法来求解系统的最优控制问题[19-20]。 本文研究的时间集结法[21]定义如下:通过分析动态系统(4)可知,嵌入链{di,i=0,1,2,…}是一个马尔可夫链,具有状态空间D以及转移概率矩阵Pu={pu(d)(d'|d)}d,d'∈D,它表示在策略u下,这个嵌入式的马尔可夫链从事件d转移到下一个事件d'的概率。在系统稳定的条件下,由式(3)可得: (5) 其中,pu(1)(2|1)=1,pu(D)(D-1|D)=1。显然,这个嵌入链是不可约的且周期为2的马氏链。则有唯一的稳态分布πu满足平衡方程:πuPu=πu和πue=1,其中e=(1,1,…,1)T是每个元素都为1的D维列向量。 根据马尔可夫模型,通过构造一个等价的马尔可夫过程,并且结合代价函数,使平均性能(2)和动态系统(4)的性能是相同的。由于系统的样本路径被各个嵌入点分隔成许多片段,因此,定义第d片段为:ζi={x(t),ti≤t (6) (7) (8) (9) 在策略u下,通过运用强大数法则[22],系统的性能表示为 (10) (11) (12) 对任意策略u有: 嵌入链对应的平均性能为 (13) 其中,δ是实数。 针对连续非线性系统的最优控制问题,通过定理1可知,新构建的马尔可夫模型可采用策略迭代算法进行求解和仿真验证。 定理1 1)对于马尔可夫模型中代价函数为(12)以及δ=ηu,策略u′优于策略u的充分必要条件是:具有代价函数(11)的马尔可夫模型,策略u′也优于策略u。 2)对于马尔可夫模型中代价函数为(11)以及最佳策略u*的充分必要条件是:马尔可夫模型中代价函数为(12)以及δ=ηu*,策略u*也是最佳的。 证明: (14) 其中,I是单位阵,gu表示在策略u的性能势向量[23]。特别地,gu的特解如下[23]: (15) 通过定理1可给出如下策略迭代算法[21]。定义uk为第k次迭代中所使用的策略,u*为最优策略。策略迭代算法的具体步骤如表1所示: 表1 策略迭代算法Tab.1 Policy iteration algorithm 通过定理1)和策略迭代理论[23],如果该算法不停止,则在每次迭代中,嵌入式马尔可夫链的性能都会得到提升。当只有有限数量的策略时,迭代过程必将停止。由定理2)可知,当迭代停止,系统将会达到嵌入式马尔可夫链的最优性能。 本文主要研究这种状态无关的特殊情况[23],代价函数为fu(x)=mx2+uTNu,其中是正实数,N是正定矩阵。在策略迭代中使用的3个变量,通过求解微分方程可得到解析解。经过计算,结果如下: 对于所有的xd-1≤x≤xd+1,1 (16) (17) (18) 其中,qp(x,u)表示从状态x∈(xd-1,xd+1)、行动为u出发的过程中,首先到达状态xd+1而不是xd-1的概率。q1(x,u)表示x∈(xd-1,xd+1)时,从初始状态x0、行动u0出发的片段期望长度,而对于其他状态x,令q1(x,u)=0。qf(x,u)表示从状态x∈(xd-1,xd+1)、行动为u开始的在一个片段上的期望代价积分,而当x∉(xd-1,xd+1)有qf(x,u)=0。下式中出现的相同符号,含义亦相同。 如果μ(u)=0,则: (19) (20) (21) 当d=1时,因为该系统是稳定的,且如前面假设的x1<0,必有μ(u)>0,于是有qp(x,u)=1,q1(x,u)=(x2-x1)=μ(u)和: (22) 当d=D和μ(u)<0时,有qp(xD,u)=0和q1(xD,u)=(xD-1-xD)/μ(u): (23) 上文已经对勒贝格采样系统的最优控制方案作了详细的阐述,下面对周期性采样方案的优化控制作简要地分析[24-25]。为了保证在其他条件不变的情况下比较两者的性能,利用勒贝格采样系统中所得平均采样间隔作为周期性采样的等采样间隔,即Δ=ti+1-ti。其中,ti,i=0,1,2,…,表示系统的采样时刻。 动态系统描述为: dx=(ax+bui)dt+σdv,ti≤t (24) 其中,ui是采样时刻ti上的控制量,在区间[ti,ti+1)上保持不变,且由系统状态决定:令xi=x(ti),则ui=u(xi)。a∈R和b∈R1×n都是给定参数,从而保证系统的可镇定性。代价函数为fu(x)=mx2+uTNu。该系统的优化问题是找到一个反馈控制律u(x)使性能(2)最小。 针对状态无关这种特殊情形,由式(24)可知,当a=0时,有: xi+1=Axi+Bui+ξ (25) 其中,A=1,B=bΔ,且ξ=σv是一个零均值,方差为Var(ξ)=σ2Δ的正态分布随机变量。 Fu(x)=Gx2+xRu+uTVu+J (26) 其中G=m,R=mbΔ,V=(1/3)mbTbΔ2+N以及J=(1/2)mσ2Δ。最优控制律是u(x)=-Lx,其中L=(1/2)(BTBS+V)-1(2ABTS+RT),并且S满足代数Riccati方程: (27) 通过求解方程(27)可以得到最优控制策略,其相对应的最优性能为η=σ2ΔS+J。 图1 基于勒贝格采样的控制策略Fig.1 Lebesgue-sampling-based control policy 为了避免初始策略选择的偶然性,对初始策略进行多组数据实验后,实验结果如表2所示。观察发现,当初始策略中间项为0时,左右两端的策略关于中间项互为相反数,且左边的控制量大于零,右边的控制量小于零时,迭代次数k=1;当初始策略为最优策略时,不进行迭代,即k=0;当初始策略偏离最优策略较大时,迭代次数也相对的增加。故而,为了快速得到较好的性能,初始策略的设定可为最优策略的形式。 表2 初始策略与迭代次数的关系Tab.2 The relationship between the initial strategy and the number of iterations 表3 两种采样方案的数据对比Tab.3 Data comparison of two sampling schemes 例2根据例1,令系统代价函数fu(x)=x2+Nu2中的正定矩阵N=0,0.1,0.2,…,1,2,3,4,10,其余参数不变的情况下,对比观察勒贝格采样系统和传统周期采样系统的性能参数变化。仿真验证,其结果分别用表4和图2表示: 表4 两种采样方案的数据对比Tab.4 Data comparison of two sampling schemes 图2 两种采样方案的性能比较Fig.2 Performance comparison of two sampling schemes 观察上面的表4,表中的最后1列表示勒贝格采样优于周期采样性能的百分比,百分比随着N的变大而减小,说明了控制能量的代价在设计控制器时显得尤为重要。由整个结果分析可知,当N>0时,系统的控制能量代价不为零,最优策略也不是max-min形式。比如,当N=0.3时,系统的最优策略为u*=[5,3,2,0,-2,-3,-5]T。 再分析图2可知,在相同的采样间隔下,当N=3时,勒贝格采样系统性能和周期采样性能有相同的效果;当N<3时,基于勒贝格采样系统的性能明显优于基于周期采样系统的性能。虽然,当N>3时,周期采样系统的性能优于勒贝格采样系统,但是,从图中可以清晰地看到,随着N的增大,平均采样间隔变化非常小,性能百分比也趋于零。 表5 两种采样方案的数据对比(N=0,0.3,3)Tab.5 Data comparison of two sampling schemes(N=0,0.3,3) 图3 系数m单独改变时的性能比较Fig.3 Performance comparison when coefficient m is changed separately 例3在例2的基础上,改变代价函数为fu(x)=mx2+Nu2的系数,其他条件亦不变的情况下,当m=0.01,0.1,1,10,100,N=0,0.3,1,3.时,得出如下结论: 通过仿真实验数据分析可得,当控制能量N=0时,无论代价函数中系数为何值时,系统平均采样间隔不变,即Δ=0.347 6s,最优策略始终为min-max形式,即u*=[5,5,5,0,-5,-5,-5]T;由表5分析可知,系统的最优性能随着的增大而增大,且倍数增加相同。从而表明了勒贝格采样系统中,与状态权值相关的代价函数不影响系统的采样间隔,但对系统的性能影响较大。再观察图3中的四个结果,比较图3a与图3b可知,当N<1时,勒贝格采样系统的平均采样间隔和两种两样方案的系统性能百分比几乎是不变的,且两种采样系统性能也都是随着成倍的增加而成倍的增大,呈正比例关系。由图3c可知,当N>1时,虽然两种采样系统的最优性能也随着的增大而增大,但也不是正比例的关系。由于图3a-图3c的选值范围较大,为了仔细分析比较两种采样方案的系统性能,针对又选择了(0,1]区间的数值。根据例2中的结果可知,当N=3时,勒贝格采样系统性能和周期采样性能有相同的效果,属于一个临界值。在细化值时,依然选择N=3。由图3d可知,当N=3,m=1时,两种采样方案的系统性能相同,从而验证了例2的结果。然而,只有当m<1时,勒贝格采样系统的性能稍微比周期采样的性能差一点。因此,整体上可得出勒贝格采样系统的性能优于周期采样系统的性能是有条件的。 通过多次仿真实验,由表6中数据可得,在控制能量代价不为零时,系统的最优性能随着的增大而增大;平均采样间隔随着的增大而减小,系统达到最优策略后也几乎不再变化。 表6 两种采样方案的数据对比(N=1)Tab.6 Data comparison of two sampling schemes(N=1) 图4 v变化时各个参量改进的比例Fig.4 Proportion of improvement of each parameter when v changes 例4在例1的基础上,假定系统的代价函数中N=0.3,其余条件不变,事件集D的值集合变为χD= {-3,-1-v,-v…,v,1 +v,3},v∈[0.2,1.8]。采用勒贝格采样,对所有的系统优化性能结果用图4表示,实线表示最化性能的比例,即各种可能的对应的最优性能比上v=1时的最优性能,虚线表示平均采样间隔的比例,即各种可能的对应的采样间隔比上v=1时的采样间隔。 由图4可知,实线斜率的绝对值小于虚线的斜率。当增加时,系统性能略微变差,但平均采样间隔也会随之增加,从而节约了计算资源。 本文研究了勒贝格采样系统的一般最优控制模型,为性能势理论在随机控制系统中的应用提供了新的解决方案。首先,通过构造等价的马尔可夫模型,提出了基于勒贝格采样的非线性系统最优控制的一般数学模型;然后,根据该模型具有马尔可夫性,编写了相应的策略迭代算法以求解勒贝格采样系统的最优策略和长期平均性能,并结合解析法得出了算法中需要用到的样本路径上片段的期望性能、片段长度和相应的转移概率;最后,仿真结果验证了在相同的采样间隔情况下,勒贝格采样系统的优化性能不仅明显要优于周期采样系统,而且基于勒贝格采样的方法更符合实际的控制系统,有效地降低了系统的采样次数并节约了系统的资源消耗。2.2 时间集结法

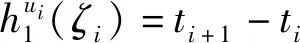

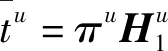

2.3 策略迭代算法



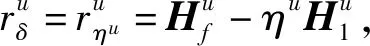

2.4 解析法
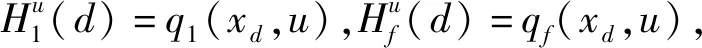
3 周期采样系统的优化控制

4 仿真结果与分析


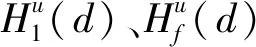
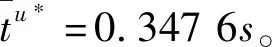






5 结论
