基于盲数理论的采空区危险性评价模型

陈怀利



基于盲数理论的采空区危险性评价模型

陈怀利1, 2

(1.金川集团股份有限公司，甘肃 金川市 737100；2.镍钴资源综合利用国家重点实验室，甘肃 金川市 737100)

房柱法开采容易造成采空区失稳事故。考虑到地质条件和开采技术条件因素对采空区稳定性产生的影响，利用综合指数法建立了房柱法开采形成的采空区危险评判模型，对采空区失稳的危险性进行综合评价分析。但由于地质情况的复杂和实验资料的不足，采空区稳定性综合评价中的影响因素普遍存在着随机性、模糊性、灰性及未确知性等不确定性。针对这一特点，将盲数理论引入到采空区稳定性评价的综合指数法中，利用盲数来表达危险指数的不确定性，提出了基于综合指数法的盲数形式，并利用盲数运算法则计算其在不同区间的可信度，从而为采空区稳定性的判断提供更充分的依据，克服了传统方法中过于绝对化的问题。实例验证表明，盲数对于采空区稳定性的判定结果更可靠。

盲数；采空区稳定性；危险性分级；综合指数法

0 引 言

采空区的存在严重威胁矿工生命财产安全[1]。近年来采空区事故频频发生，不但引起国家和社会的高度关注，而且也引起了人民群众的广泛关注。如2014年在乌鲁木齐发生的某煤矿采空区冒落灾害，造成了16死11伤的惨况；又如2013年河北某矿业公司发生的采空区塌陷事故，导致6名井下工人被埋。采空区对工人危害严重，如何防止采空区威胁是目前矿业区安全监管的热点[2]，而对采空区稳定性正确评价是其采取正确治理方法的前提。

采空区稳定性评价方法很多[3−4]。如文献[5]在构建采空区稳定指标体系影响的基础上，采用非线性科学的突变理论建立了采空区风险评价模型。文献[6]建立了残余沉降的多变量离散灰色预测模型。

目前工程上较为常用的方法是模糊综合评判方法[7]。该方法考虑了房柱法开采采空区灾害事实，从地质及开采技术条件方面分析了影响采空区稳定的各种因素，并确定权重，建立采空区危险源综合指数模型，但由于技术及经济的限制和地址条件的复杂性，使采空区危险性预测评价中的参数往往具有不确定性。刘开第[8]提出了一种新的数学方法来解决参数的不确定性问题，使之能更好地反映客观因素的不确定性。本文基于采空区危险性评价中广泛使用的综合指数法，将盲数理论与之结合，更充分地判断采空区危险状态。

1 盲数的概念及其运算

1.1 盲数的定义

设a∈,表示有理灰数集；a∈[0, 1]，=1，2，…，，若：

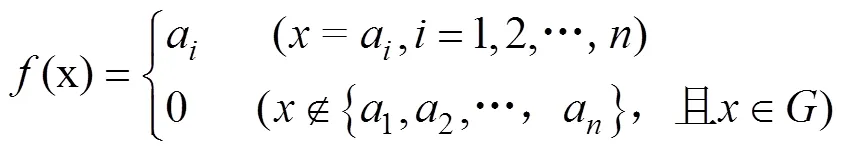
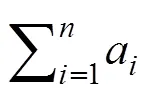
1.2 盲数的运算

盲数的运算抽象于盲信息之间的真实关系，设*代表有理灰数集的一种运算，或为加或为减或为乘或为除。

设有盲数、为：

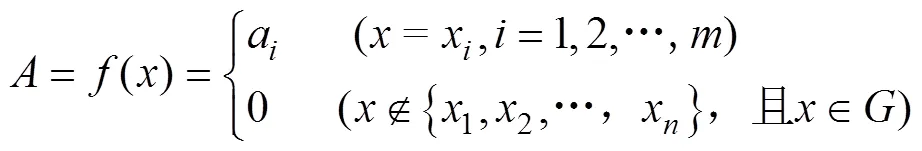
式中，1，2，…，x和1，2，…，y分别为与的可能值序列：1，2，…，α和1，2，…，β分别为与的可信度序列。

称为与的可能值*矩阵。

称为与的可信度积矩阵。

与的可能值*矩阵与可信度积矩阵中，元素a、b(=1，2，…，；=1，2，…，)称为相应元素，其所在位置称为相应位置。

1.3 盲数的可信度

若、为盲数，则×=的可信度为

同理，1≤×≤2的可信度为

式中，、1、2为工程实际问题中所定的常数。

2 采空区稳定性的盲数评价模型

影响采空区稳定的主要因素有地质方面的因素(如开采深度、开采厚度、矿体倾角、顶底板岩体质量指标值、上覆岩层弹性模量、上覆岩层单轴抗压强度、矿石单轴抗压强度、构造应力、节理条件、地下水状态等)，也有开采技术方面的因素(如矿区开采面积、采空区面积、采矿方法、顶板管理方式、爆破方式等)。根据这些采空区影响因素的分析，确定采掘面周围采矿地质条件的每个影响因素对采空区的影响程度，以及确定出各个因素对采空区危险状态的影响指数，将它们综合起来就能得到采空区危险状态等级评定的综合指数，为解决采空区威胁问题打下基础。

2.1 采空区危险程度的地质因素及评分标准

由地质因素评判采空区危险程度时，主要考虑以上10个地质因素，设1为由主要地质因素综合得到的采空区危险程度综合性指数，Gmax为第个地质因素最大危险状态取值，G为第个地质因素赋值，n为因素的序号。

采用式(9)即可通过计算得到由地质因素确定的综合指数1。

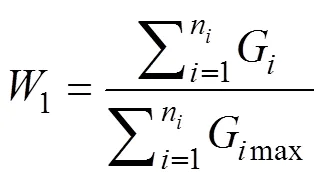
2.2 采空区危险程度的开采技术因素及评分标准

由技术因素评判采空区危险程度时，主要考虑采矿技术、开采参数及开采重复影响3方面。其中，采矿技术主要包括采矿方法、爆破方法和空区处置方法；开采参数则包括开采区域面积、空区面积、矿柱宽高比及矿柱面积等；而开采重复影响包括是否发生过大规模采空区事故，采动重复次数等。综合以上10个技术因素，得出评定采空区稳定等级综合指数的计算公式为

式中，2为由开采技术因素得到的采空区危险程度指数，Mmax为第个开采技术因素最大危险状态取值，M为第个开采技术因素赋值。由式(10)即可得出由开采技术因素所确定的采空区危险程度指数2。

2.3 采空区危险程度的综合指数W及盲数下的W

依据综合指数法，采空区危险程度的综合指数可由主要地质因素综合得到的采空区危险程度综合性指数1与开采技术因素得到的采空区危险程度指数2取最大值得到，算法见式(11):

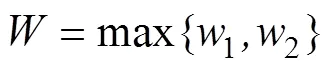
式(11)中，考虑到一些因素指标的不确定性及复杂性，在计算采空区危险程度的综合指数时，可以借助盲数这个数学工具，得到盲数形式的采空区危险程度的综合指数，使结果更准确，计算式如下所示：

2.4 采空区失稳状态的危险性等级

大面积采空区危险性差别不明显，但为了对采空区危险性进行描述，使人们能更好地区分和了解不同采空区危险程度的不同，依据相关研究成果和综合指数法，并结合以往经验，可以将采空区危险性分为4级[11]，其相关危险性等级及指数评定如表1所示。

表1 采空区危险等级划分及相关指数评定

3 实例应用

荆门某石膏矿层直接顶板为粉砂质泥岩或石膏泥岩，盐性差，平均倾角为9°，矿层的平均厚度膏层为5.6 m，且矿体埋藏浅。采用房柱式开采方法。据设计和调查，其主要参数为：矿房长轴一般为50~70 m，顶柱为6 m，矿房宽度为7 m，矿柱宽度为5 m，间柱宽度为5 m。其顶部留有1.5 m厚石膏作为护顶层[12]。

为合理评估采空区危险性，采用综合指数法，将不同危险性赋予不同的取值，根据危险性取值即可判断其危险性大小，对不同条件状态下的采空区进行危险性评价，即将危险性量化为危险指数，采空区危险状态评定指数见表2。

由于影响因素指标的测定存在不确定性和随机性，其中上覆岩层单轴抗压强度和矿石单轴抗压强度这2个因素的取值范围跨越了2个危险指数区间，具有显著的盲数性质，所以可以将盲数理论应用到综合指数算法中，为采空区危险性的判定提供更准确全面的依据。

定义上覆岩层单轴抗压强度R的危险指数6为盲数，矿石单轴抗压强度R的危险指数7为盲数，则可求得：

表2 地质条件确定的采空区危险状态评定指数

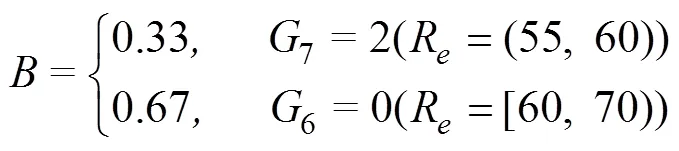
式(13)、式(14)的数学意义：上覆岩层单轴抗压强度R的危险指数6取值为4的可信度为0.33，取值为2的可信度为0.67；同理，矿石单轴抗压强度R的危险指数7为2的可信度为0.33，取值为0的可信度为0.67。将它们按照盲数运算法则代入式(12)进行计算，可以得到由地质条件确定的采空区危险性评定指数1的盲数表达式。

由式(15)可知，由地质条件确定的采空区危险性评定指数1为0.5的可能性为0.1089，为0.4355的可能性为0.4422，为0.371的可能性为0.4489。

再由表3知，由开采条件确定的采空区危险性评定指数2=0.74，由式(12)知，当1=0.5，2=0.74时，为最大值0.74；当1=0.4355，2=0.74时，为最大值0.74；当1=0.371，2=0.74时，为最大值0.74；进而得到其综合指数的盲数表达式为

()=1 (=0.74)

即综合指数取值为0.74，根据表1中采空区危险等级划分及相关指数评定知，此采空区属于Ⅱ级重大危险源(重大危险性)。以上计算过程，比较全面准确地反映了由地质条件确定的采空区危险性评定指数1在各个不同取值区间的可能性，避免了由参数单一导致的计算偏差问题，使最后得到的综合指数更具说服力，从而能更全面地判断采空区危险状态。

表3 开采技术确定的采空区危险状态评定指数

4 结 语

采空区危险状态的判定很复杂，许多影响因素取值具有不确定性，再加上地质资料的不足，使之成为一种盲信息。本文提出用盲数来描述采空区危险状态判定中的不确定因素的危险指数，并利用盲数计算方法求得由地质条件确定的采空区危险性评定指数。与以往的单单用综合指数法确定相比，盲数可以将各种评判指数的可能情况用可信度表示，对影响因素考虑周全。将该法用于实际工程，会使预测结果更加全面可靠，为采空区危险判定的全面性、准确性和科学性提供了新途径。

[1] 程爱宝,王新民,刘洪强.灰色层次分析法在地下采空区稳定性评价中的应用[J].金属矿山,2011(2):17−21.

[2] 杜 坤,李夕兵,刘科伟,等.采空区危险性评价的综合方法及工程应用[J].中南大学学报:自然科学版,2011,42(9):2802−2811.

[3] 胡洪旺,叶义成,赵祖炜,耿宏波.基于Ressiner厚板理论的采空区顶板稳定性研究[J].矿业研究与开发,2018,38(07):66−70.

[4] 杨美宏,李占金,郝家旺,郭廷儒.大梨树沟铁矿采空区对地表稳定性影响分析[J].矿业研究与开发,2018,38(06):40−43.

[5] 马海军,黄德镛.基于突变理论的采空区风险评价模型研究[J].科学技术与工程,2010,10(22):5369−5373.

[6] 王正帅,邓喀中.老采空区残余沉降的离散灰色预测模型[J].煤炭学报,2010,35(7):1084−1088.

[7] 马云龙,刘铁雄,陈科平,等.高峰105号矿体采空区稳定性模糊综合评价[J].西部探矿工程,2010(6):1−3.

[8] 刘开第,吴和琴,庞彦军,等.盲数的概念、运算与性质[J].运筹与管理,1998,7(3):14−17.

[9] 赵志峰,徐卫亚.基于盲数理论的边坡安全稳定分析研究[J].岩土力学,2007,28(11):2401−2404.

[10] 高 峰,张志镇,高亚楠,等.基于盲数理论的冲击地压危险性评价模型[J].煤炭学报,2010,35(S):28−32.

[11] 刘如铁,李 文,李 杰.煤矿大面积采空区失稳危险源分级[J].煤矿安全,2012,43(5):143−146.

[12] 康钦容,张卫中,倪小山,等.采空区稳定性评价的综合指数法[J].金属矿山,2017(3):162−165.

(2018−09−30)

陈怀利(1963—)，男，安徽砀山人，高级工程师，硕士，从事采矿工程设计，Email: 524706133@qq.com。