基于观测路径相似性粒子滤波在陀螺数据处理中的研究

贺凯盈，王 涛，李燕敏，谢忠俍

(陕西铁路工程职业技术学院，陕西 渭南 714099)

磁悬浮陀螺全站仪是一种将磁悬浮陀螺寻北装置与全站仪智能集成，通过敏感地球自转从而独立测定真北方位的定向仪器[1]。在实际工程应用中通过传感器采集到的信号往往会受到诸如白噪声、温度、风振等因素的干扰，为了有效地消除这些干扰因素对GAT陀螺全站仪观测数据的影响，提高陀螺定向的精度，需对采集的信号进行降噪滤波处理。有利用小波分析法对仪器采集的转子电流观测数据误差进行剔除，有效的从强噪声干扰转子电流数据中提取用于计算定向角的有效数据，较好地改善仪器的定向结果；有将渐消因子引入到自适应滤波算法中，运用渐消自适应Kalman滤波算法处理磁悬浮陀螺全站仪系统采集的转子电流值，对仪器定向精度的提高有一定的作用[2-4]。然而一直存在这些滤波方法适用范围不够广的弊端。本文是基于磁悬浮陀螺全站仪的转子电流数据的随时间动态变化、显著的长记忆系统性特征，采用观测路径相似性的粒子滤波算法优化数据质量，进而达到提高陀螺定向精度和稳定性的目的。

1 粒子滤波基本原理

1.1 动态系统的空间模型

状态空间模型包括两个模型：一是系统模型，反映动态系统在输入变量作用下在某时刻所转移到的状态；二是输出或观测方程模型，将系统在某时刻的输出和系统的状态及输入变量联系起来[3]。

系统模型：xk=f(xk-1,uk-1)

(1)

观测模型：yk=h(xk,vk)

(2)

f(·) 和h(·)是已知函数，系统噪声uk和观测噪声vk这两个随机变量的概率密度是已知的，xk是系统在k时刻的状态变量，yk是xk对应的观测值，uk和vk是独立的并且和系统状态是不相关的。

式(1)和式(2)所构成的状态空间模型描述如下。

和系统模型相对应的状态转移概率密度：

p(xk|xk-1)

(3)

和观测模型相对应的观测值似然概率密度：

p(yk|xk)

(4)

并且基于状态xk服从一阶马尔科夫过程，观测yk相互独立，p(x0)为已知系统状态的初始先验密度。状态空间模型在刻画系统内部状态基础上可以表达系统内部和外部的输入输出变量之间的联系，还可以把多个变量时间序列转换为向量时间序列后处理输入输出变量的建模问题。

1.2 粒子滤波算法

序贯重要性采样作为粒子滤波的基础，将统计学中的序贯分析方法应用到蒙特卡罗方法中，从而实现后验滤波概率密度的递推估计。将重要性概率密度函数q(x0:k|y1:k)转化为：

q(x0:k|y1:k)=q(x0:k-1|y1:k-1)q(xk|x0:k-1,y1:k)

(5)

假定系统状态满足一个马尔科夫过程，观测值相互独立，可得：

(6)

递推形式的后验概率密度函数如下：

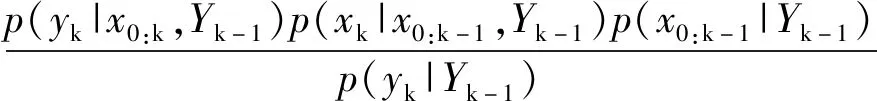
(7)

(8)

粒子权值归一化处理公式如下：

(9)

序贯重要性采样算法从重要性概率密度函数中生成采样粒子，并随着测量值的依次到来递推求得相应权值的状态估计，通常希望粒子权值的方差尽可能趋近于零。克服序贯重要性采样算法权值退化现象最直接的方法是增加粒子数，而这会造成计算量的相应增加，影响计算的实时性。因此，一般采用选择合适的重要性概率密度函数和在序贯重要性采样之后采用重采样两种方法[5-6]。

1.3 基于观测路径相似性的粒子滤波算法模型

由于陀螺仪转子动态系统对环境的高度敏感性，转子电流数据序列可以认为是对环境因素的真实记录。当观测噪声较小时如果一个粒子的观测值路径靠近系统状态的观测值路径，则该粒子的路径靠近系统状态的路径的概率更大[7-9]。我们可以计算这两种观测值路径之间相似性的程度，当相似性程度较高时，表示该粒子接近系统状态的程度较高，反之，则表示该粒子接近系统状态的程度较低。利用该相似性程度去修正粒子的权值，以期望获得更高的非线性系统状态估计精度[10-12]。在处理转子电流数据时，两种观测值之间的相似性衡量的主要依据是转子电流相关性的皮尔逊相关系数和样本自相关函数，划分两种观测值路径的依据是转子电流数据序列中突变的时刻和周期性[13]。

基于观测路径相似性的粒子算法的执行步骤如下。

1)预测：同标准粒子滤波算法一样，从系统状态转移概率密度中抽取新粒子：

2)更新：计算权值wk(i)和wk-L+1(i)，估计系统状态xk和xk-L+1如下:

该算法由预测、更新和平滑组成，无重采样步骤，从而也避免了粒子多样性匮乏问题。通常，粒子滤波算法的粒子权值公式由两部分的乘积得到。其中，第1部分为该粒子在k-1时刻的权值；第2部分为一个分数式。第1部分主要体现了该粒子在k-1时刻的优良性；第2部分体现了该粒子在k时刻的优良性[14-16]。

2 实例分析

2.1 数据来源

某项目工程中包含长达6 km的海底沉管隧道，是完全依靠多节预制的管道进行对接而成，施工难度极大。为保证隧道新沉管节和已沉放管节的安全对接、沉管隧道的最终顺利贯通，沉管隧道管节沉放控制标准要求精度很高，沉放对接期间贯通偏差设计要求小于50 mm；最终接头贯通面偏差小于35 mm，其横向贯通限差要求要远高于现有规范要求。选择该工程项目中3种比较典型的外界环境下采集的数据进行分析滤波处理：①观测条件比较平稳良好，无明显外力影响；②观测环境比较恶劣，有较大风力持续或车辆偶然经过对采集数据的过程产生影响；③在观测条件比较良好的情况下，有较小的风力影响或由于场地限制，架设仪器周围不够稳定的影响(每种情况各选两个数据文件，文件名依次命名为1.DAT，2.DAT，3.DAT，4.DAT，5.DAT，6.DAT)。

2.2 数据滤波模型

基于转子电流在观测条件较差时，观测数据序列受到显著干扰，甚至发生大幅度数据跳变；观测序列本身表现出明显的长记忆和非线性特征，表现为数据序列具有显著的自相关函数与偏自相关函数计算结果；观测序列一阶差分数据总体上具有方差与均值的平稳性，但仍然表现出明显的有色噪声性质，说明差分数据序列中既有白噪声成分又有明显的有价值信号成分存在。顾及此观测序列特征建立基于观测路径相似性的粒子滤波模型，如公式(10)所示。

式(10)中系统状态表示为电流数据x，一阶导数v，二阶导数a，v和a根据电流观测序列推算，观测值噪声和模型误差噪声利用开窗法估计。v和a初值设为0。观测值噪声和模型误差噪声初由精寻一、二位置的各前200数据求得。x初始状态设为前200个观测值的均值，粒子数取300[17-19]。平稳状态下的时间间隔L可以设置在500～1 000内；突变情况下的数据划分是在突变发生前计算，原则是时间间隔L不包含突变影响的持续时间段；具有一定周期的数据序列划分是基于周期性的长短[20-21]。

转子电流自适应滤波结果见图1，转子电流标准粒子滤波结果见图2，转子电流基于观测路径相似性粒子滤波结果见图3，3种滤波前后方差结果对比见表1，3种滤波前后均值结果对比见表2。

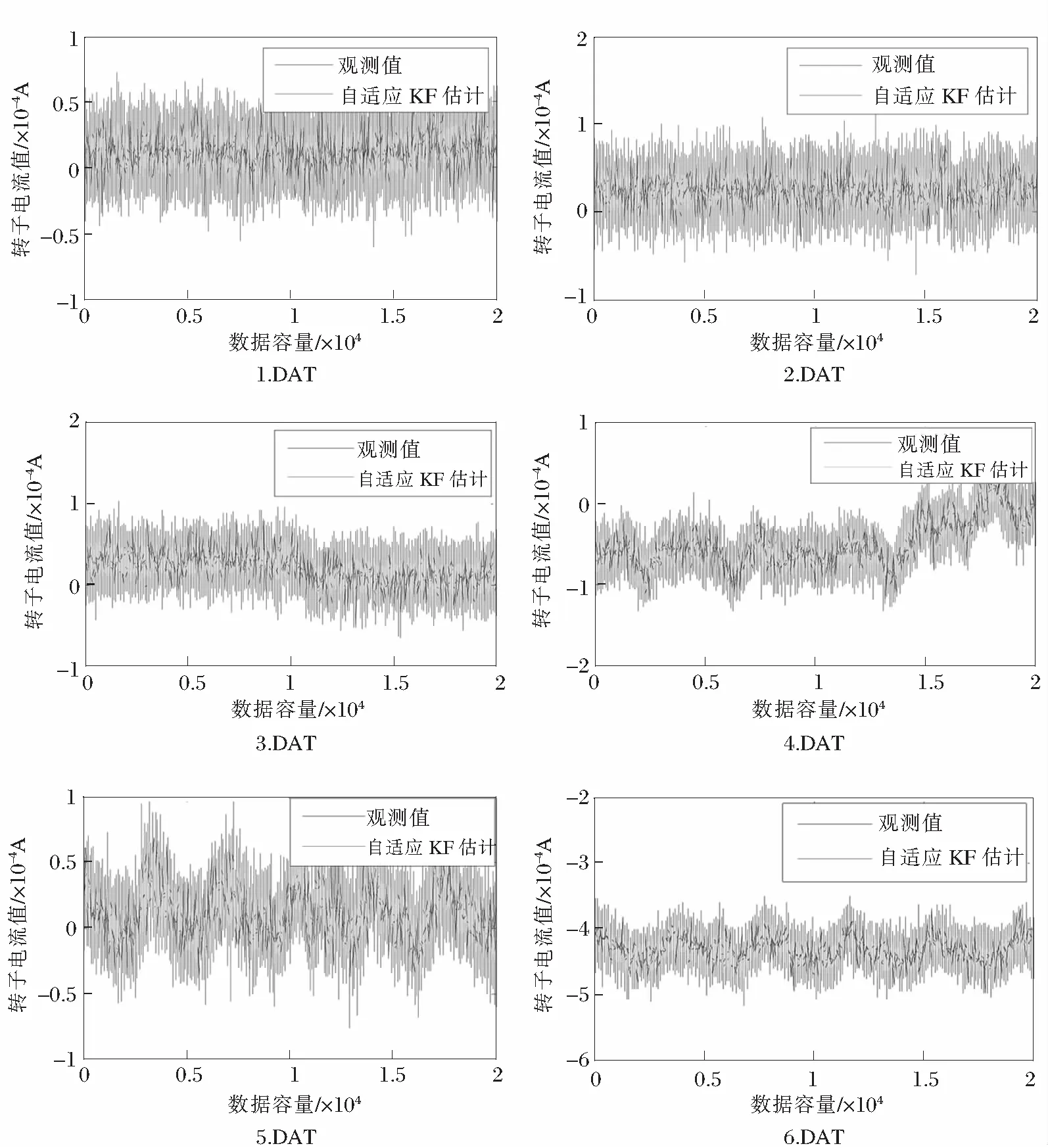
图1 转子电流自适应滤波结果

图2 转子电流标准粒子滤波结果

图3 转子电流基于观测路径相似性粒子滤波结果

数据文件原始数据观测方差标准粒子滤波后方差自适应KF滤波方差基于观测路径相似性粒子滤波后方差1.DAT4.8916e-0102.1982e-0102.1634e-0101.3526e-0102.DAT4.9195e-0102.7526e-0102.8074e-0102.0485e-0103.DAT5.3513e-0103.7053e-0101.4253e-0108.9563e-0114.DAT9.2332e-0102.3845e-0107.9652e-0109.1426e-0115.DAT4.6365e-0103.3043e-0103.1457e-0102.5762e-0106.DAT4.8916e-0103.2898e-0103.2478e-0103.1024e-010

表2 3种滤波前后均值结果对比

由图1～3、表1～2分析可以得出：3种典型环境下采集的原始数据在3种不同的滤波算法的处理下数据离散度都得到了不同程度减小，其中基于观测路径相似性粒子滤波算法处理后，数据方差整体最小，最小值为8.956 3e-011；标准粒子滤波后方差和自适应卡尔曼滤波后方差相对于原始观测数据整体都有减小，但是两者的滤波性能相当。3种滤波方法后的均值相较于原始数据也有了小幅变化，提高了陀螺定向的精度和在极端工作环境下的稳定性。

3 结 论

3种滤波方式都明显减弱了转子系统的高频噪声影响，都有不同程度的优化数据质量。从数据方差大小比较，整体上粒子滤波后的数据具有更高的噪声集中程度。在处理比较平稳状态下的转子电流和具有一定周期的转子电流数据上，标准粒子滤波和自适应滤波的效果相当；在处理异常条件下的具有突变特征转子电流数据时，基于观测路径相似性滤波算法的效果优于自适应卡尔曼滤波和标准粒子滤波算法。这种结果的产生经过分析可认为是观测条件的突变对转子系统的影响过程会有记忆性，自适应卡尔曼滤波和标准粒子滤波算法只能减弱这个持续过程的影响。

基于观测路径相似性的粒子滤波效果在不同类型的转子电流序列中表现优越性程度不一致，首先是异常突变情况下的数据优化效果更为明显，其次是有一定周期的数据序列，最后是较为平稳的数据序列。分析认为是该算法在衡量数据相关性之后，如果数据出现异常跳动时，仍能以较大的概率将权值赋给正常状态采集下的数据样本，降低了异常突变下数据混入到平稳数据序列中的可能性。