无速度传感器永磁同步电机转速估计的研究

彭雨豪，陈超波，黄姣茹

（西安工业大学 电子信息工程学院，西安710021）

目前，永磁同步电机在人们日常生活中必不可少，成为整个工业革命的核心。随着科学技术的进步，各个领域研究的快速发展，人们对电机性能的要求越来越高。然而无论如何使用电机，都需要精确地掌握电机的转速和转子位置，以便监测系统的稳定性并加以控制。当前，在传统的永磁同步电机控制中，要检测到电机的转速与转子位置，就必须在电机轴上安装一个速度传感器[1-2]。如果增加机械传感器，会使电机轴体变大，相关的维修变得复杂，且容易受恶劣环境的影响，导致系统运行稳定性变差。这使得无速度传感器技术有了发展空间[3-4]。

近年来，诞生了多种智能估计算法，文献[5]提出的动态转速估计法，包含转子磁通估计和转子反电势估计2 种方法，存在对电机的参数变化敏感等缺点；文献[6-7]提出的神经网络法，使用误差反向传播算法的自适应律估计转速，电流模型转子磁链观测器被神经网络所替代，电机参数来源于网络的权值，但计算量大，实现其硬件尚有难度。还有如滑膜观测器法[8-10]、自适应估算法[11-13]等，同样计算过程较为复杂，需要具备数据处理较好的硬件设施。基于此，提出了算法简便且可保证精度的估算方法，即基于扩展卡尔曼滤波方法。

1 无速度传感器永磁同步电机系统模型

永磁同步电机的数学模型不仅是一个非线性系统模型，同时也是一个强耦合的多变量系统模型。为建立正弦波永磁同步α-β 轴两相坐标系，必须满足一定条件，假设：①忽略电机铁心的饱和；②不计电机中的涡流和磁滞损耗；③电机的电流为对称的三相交流正弦波电流。

由电机数学模型的转换关系，可得永磁同步电机α-β 轴下的数学关系为

电压方程

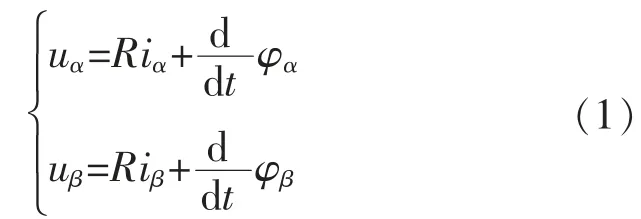
磁链方程

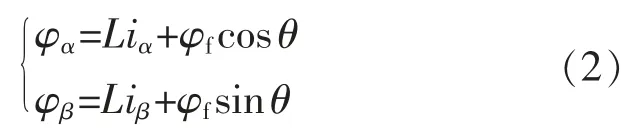
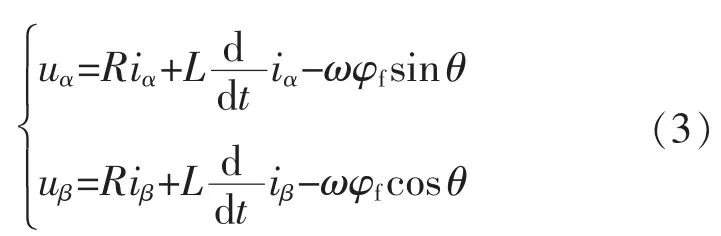
式中：uα和uβ，iα和iβ分别为两相静止坐标系下的定子电压、定子电流；R 为定子电阻；L 为定子电感；φf为转子磁链；ω 为机械转子角速度；θ 为转子位置角。

式（3）为根据数学建模得出的永磁同步电机参数关系式，将其改写为卡尔曼滤波模型的形式：

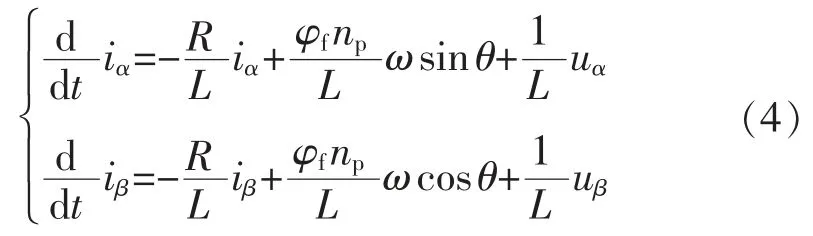
取

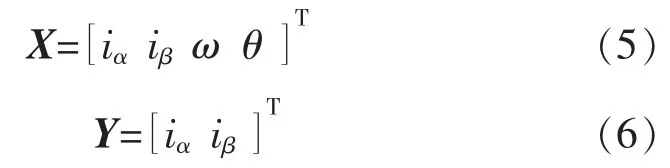
式中：X 为状态变量；Y 为系统观测变量。

由于永磁同步电机系统中受到环境变化、电压波动以及存在测量噪声等干扰因素，因此在系统模型中考虑噪声Wk和Vk。建立离散化后的系统模型为

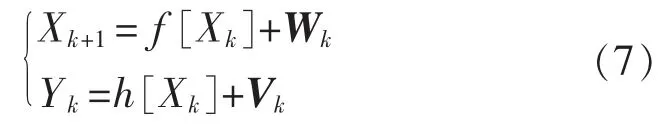
其中

叶晓晓看着自己的父亲，他暴跳如雷，两手鲜血淋漓的，他不知道，为了买那只剃须刀，叶晓晓舍弃了三条裙子和一件T恤。那一刻，她心里也有些许的恨意升上来，眼泪也一滴一滴地掉下来，滴到她的膝盖上，滴到抱着膝盖的手指上。

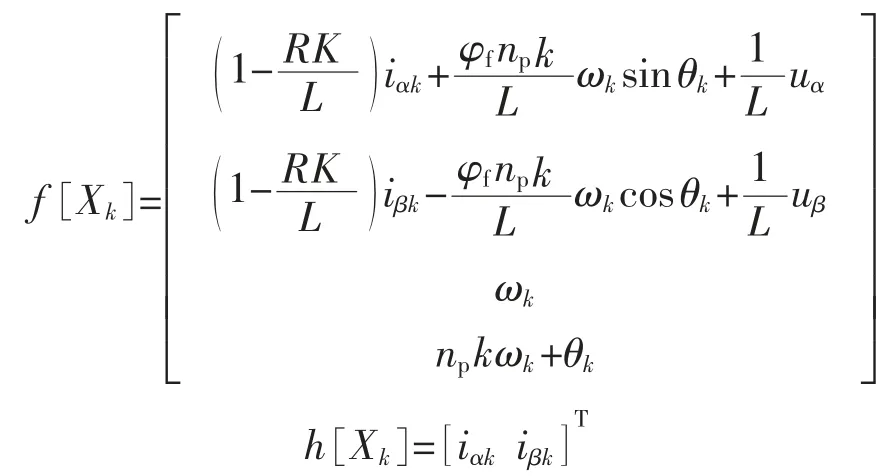
式中：Xk为k 时刻的状态变量；Yk为k 时刻的观测变量；f［Xk］为非线性函数；h［Xk］为线性函数；np为电机的极对数；Wk和Vk分别为系统噪声和观测噪声，且服从均值为零、方差各为Q和S 的不相关高斯白噪声。

2 扩展卡尔曼滤波算法

在实际情况中，系统总是有不同程度的非线性关系。针对非线性系统，卡尔曼滤波已不再适用，因此推广出扩展卡尔曼滤波算法。其核心思想是，首先围绕滤波值X 将非线性函数f和h 使用泰勒展开，略去二阶及以上项，得到一个近似的线性化的模型，然后应用卡尔曼滤波完成对目标的滤波估计等处理。

在此所提出的估算方法就是基于扩展卡尔曼滤波方法，将标准卡尔曼扩展至非线性系统领域，使其可以运用到电机模型中。只需采集电机的固有信息便可准确估算出电机的转速。

考虑离散系统的动态方程式（7），将非线性函数f（*）围绕滤波值Xˆk做一阶Taylor 展开，得到

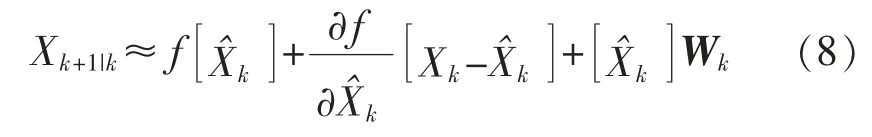
令，

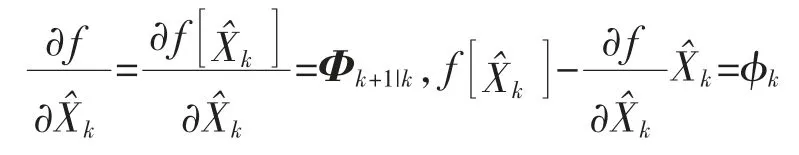
因此经过线性化处理的状态方程为

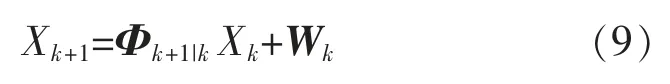
同理，可得线性化的观测方程为：

其中

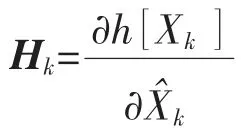
对线性化后的模型（9）和（10）应用卡尔曼滤波基本方程，可得扩展卡尔曼滤波递推方程，递推公式如式（11）～式（15）：

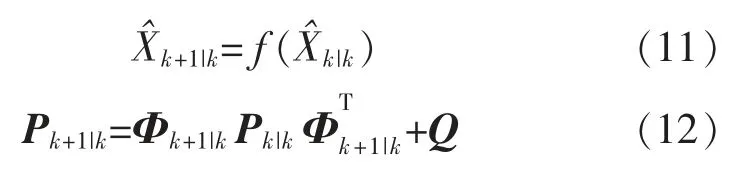
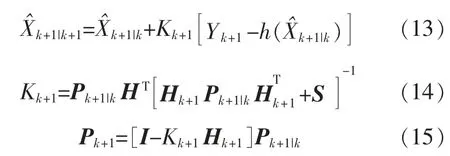
式中：I 为n 维的单位矩阵。

扩展卡尔曼滤波算法的流程如图1所示。

该算法的状态估计分为预测和校正2 部分，最优滤波估计值=预测估计值+修正值。算法的第1 部分，通过给定系统的初始状态变量，以及初始协方差矩阵进行一步预测，得出k+1 时刻状态和协方差的估计值；第2 部分，通过测量得到的观测值修订一步预测所得到的估计值，计算出k+1 时刻的滤波值。其中包含状态与协方差的更新以及卡尔曼增益的计算。如此循环2 个部分，最终得出系统状态的最优估计值。

3 仿真与分析

所使用的永磁同步电机参数见表1。永磁同步电机的转速估计的仿真模型如图2所示。

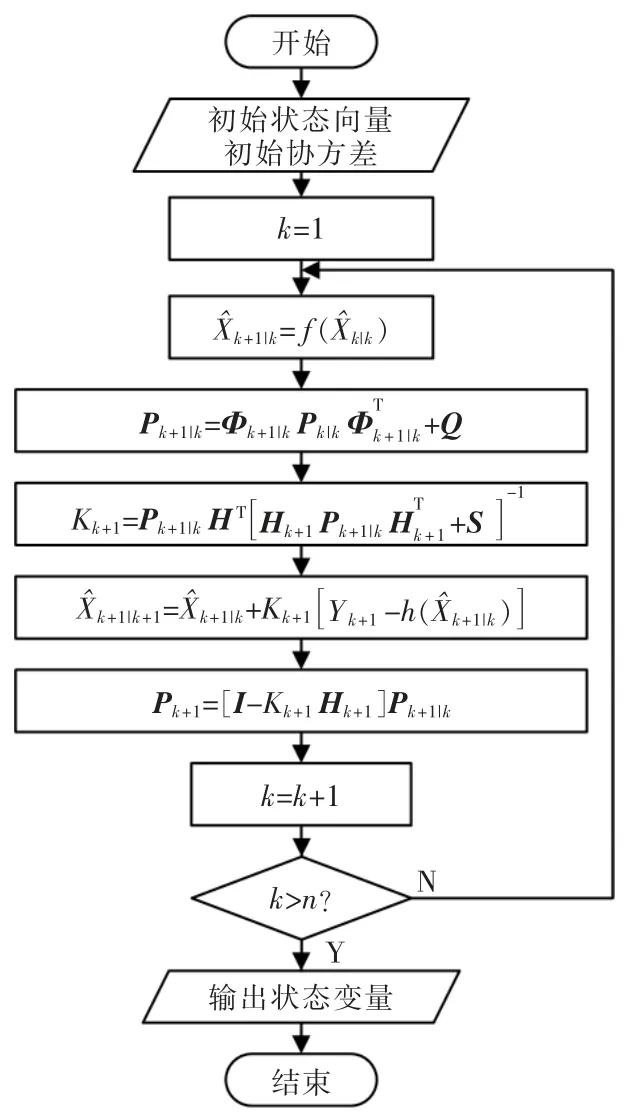
图1 扩展卡尔曼滤波算法流程Fig.1 Flow chart of extended Kalman filter algorithm

表1 永磁同步电机系统参数Tab.1 System parameters of permanent magnet synchronous motor

图2 由上下2 部分组成：上半部分为永磁同步电机模型；下半部分为扩展卡尔曼滤波算法部分，其左端输入的是电机2 项静止坐标轴下的定子电压和电流，经过扩展卡尔曼算法估算（S 函数形式），最终在最右端的综合示波器表示电机真实波形与卡尔曼估计的波形作对比。

扩展卡尔曼滤波器的参数如下：

1）初始状态向量

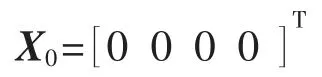
2）状态转移矩阵

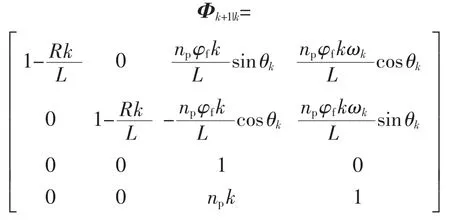
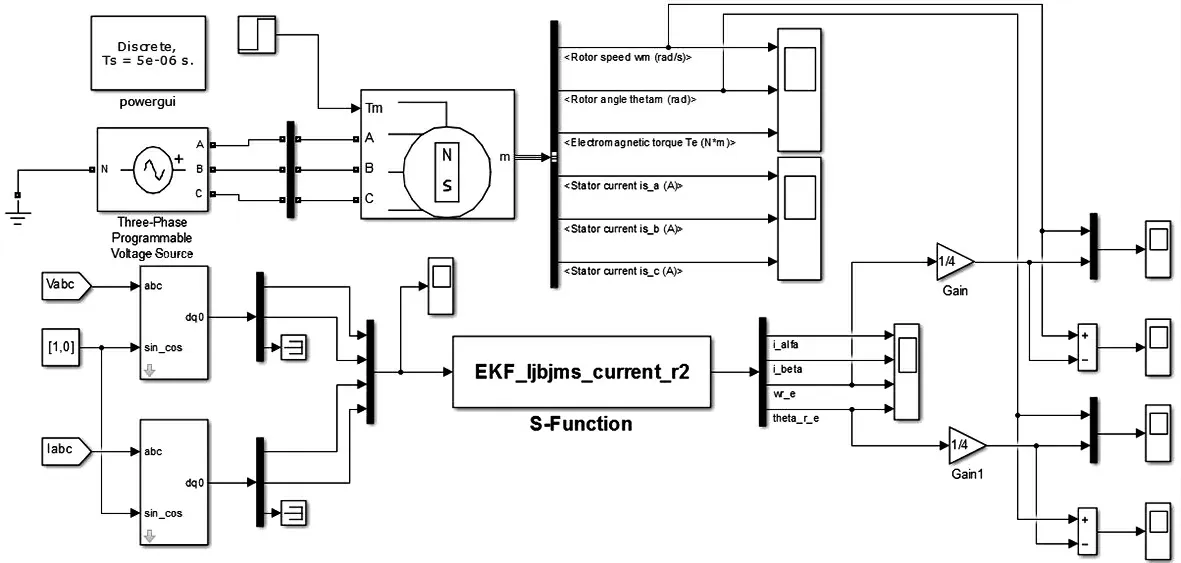
图2 扩展卡尔曼滤波仿真模型Fig.2 Extended Kalman filter simulation model

3）观测矩阵

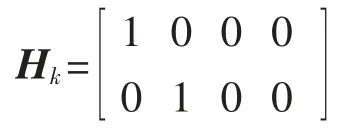
4）初始协方差矩阵

5）方差

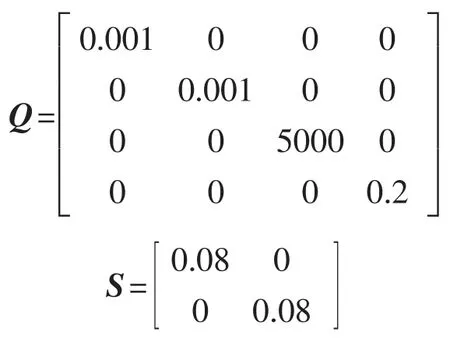
基于表1所给电机参数，对算法进行仿真验证。结果显示，电机的电角速度为314 rad/s，由于仿真所采用的永磁同步电机的极对数为4，因此电机的机械转速为78．5 rad/s。

电机转速对比的仿真结果如图3所示。由图可见，当转速上升时扩展卡尔曼滤波估计值稍有延时，短暂时间后，估计转速与真实转速几乎重合，由此可见扩展卡尔曼滤波算法可以很好地估算电机的转速。当噪声较小时，估计值能迅速地跟踪真实值，从而尽早给出可靠的转速数据值。电机转速误差如图4所示。由图可见，转速的误差在0．1 s 时基本无误差，估计值几乎等于真实值。

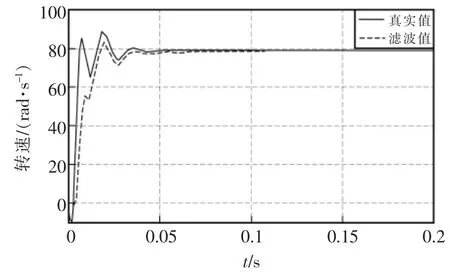
图3 电机转速对比Fig.3 Comparison of motor speed

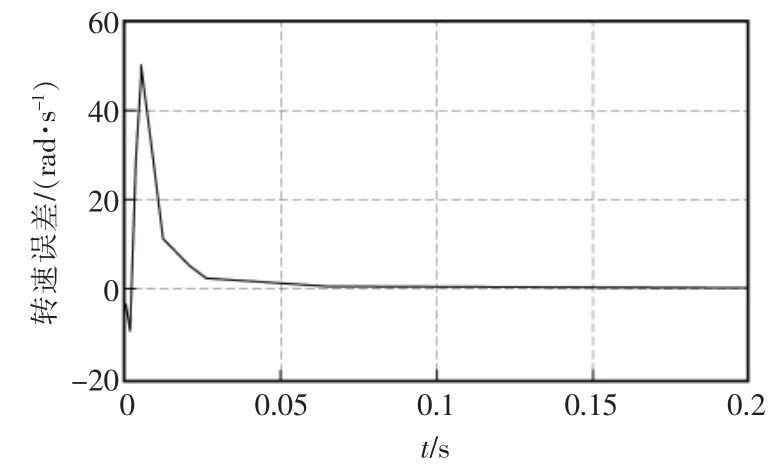
图4 电机转速误差Fig.4 Motor speed error

基于此可以看出，采用卡尔曼滤波算法可以对电机的转速进行很好的预估，从而省去了速度传感器的安装，简化了电机结构。

此外，设定电机在0．1 s 时突然提高转速，并在0．25 s 时降至原值。以此测试当电机转速有所变化时，扩展卡尔曼滤波算法是否可以精确地估算出电机参数。转速突变估计及电机转速误差的仿真结果如图5和图6所示。

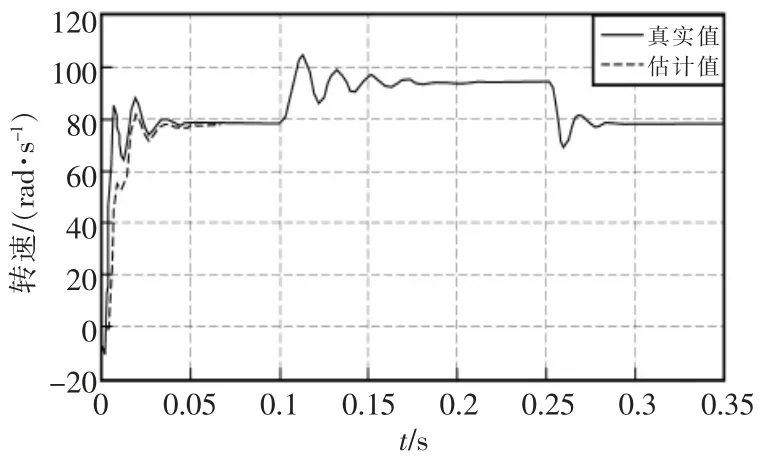
图5 转速突变估计Fig.5 Speed mutation estimation

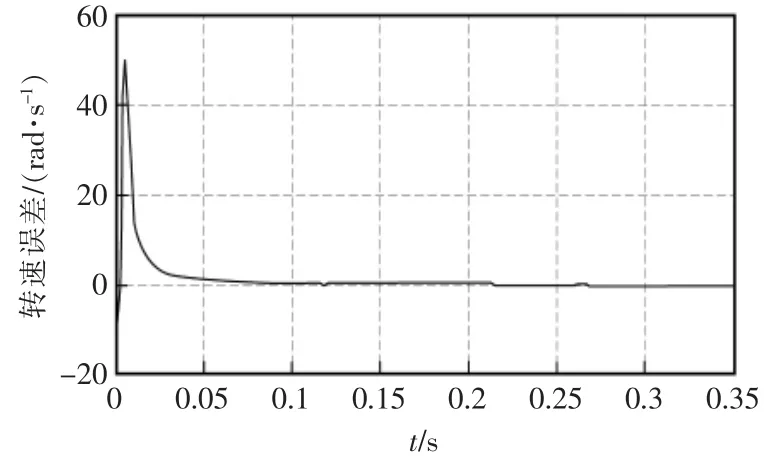
图6 电机转速误差Fig.6 Motor speed error

由图可见，即使电机在途中调速，而且估计误差波动的范围很小，该滤波器依然可以精确地估算出转速。由此验证了在系统多变的情况下滤波器精准且高效的估算能力。

4 结语

在该滤波算法的设计中，永磁同步电机是一个复杂的非线性系统。针对这类系统，将卡尔曼滤波算法进行扩展，使其可以解决与非线性系统的相关问题。该算法不但估计精确而且运算简便。扩展卡尔曼滤波着实为最优估计滤波，对于永磁同步电机系统，依旧可以很好地估算出电机转速。因此，采用无速度传感器，可以取代传统机械传感器，简化数据的测量过程。