自动缝合关节机器人的动力学分析与仿真

张劲松，何 勇，吴 栋，梁艺荧

（东华大学 机械工程学院，上海201620）

人工操作织物衣片进行对目与拼合需要将衣片的线圈口撑开，一一对应地套入到缝合机上的对目针上，再利用缝针进行缝合。这种传统工作方式容易出现错针、漏针等问题，影响衣片的缝合质量，且对操作人员的要求比较高，对操作人员的眼睛伤害较大，员工工作周期短，生产成本较高。应用自动缝合关节机器人控制织物衣片进行自动对目、拼合及缝合，有利于保证产品质量，提高生产效率，降低成本。

目前，国内外未见有关自动缝合关节机器人研究的相关报道，但对于普通机器人的分析研究很多。当前研究机器人动力学的常用方法有拉格朗日法[1-2]、牛顿-欧拉法[3]、Kane 方程[4]及虚功原理[5]等。文献[6-7]在采用牛顿-欧拉法对机器人进行动力学分析的基础上，应用MatLab 计算出机器人各关节的驱动力矩，再利用仿真软件对机器人进行动力学分析与仿真；文献[8-9]应用SolidWorks和ADAMS 进行联合建立机器人的动力学仿真模型，并进行动力学仿真分析，得到相关的性能曲线图。然而这些研究未能对最优运动轨迹下的关节峰值力矩进行求解以及仿真验证。

在此，以自动缝合关节机器人为研究对象，采用拉格朗日法建立机器人的动力学模型，求解机器人各关节的理论驱动力矩，并应用MatLab 进行轨迹规划，应用ADAMS 对机器人进行动力学仿真分析。

1 机器人三维模型的建立

1.1 本体结构设计

根据织物衣片自动对目与拼合的工作原理，设计了一种可以控制末端构件在三维空间内运动，且能够柔性抓取和放下物体的自动缝合关节机器人。该关节机器人具有5 个自由度，用于实现末端构件在水平面空间内的定位、定向，以及在垂直水平面的方向上做上升下降运动。关节机器人的构型具有结构简单、轻小的特点；主要由关节外壳、电机和减速器组成，且外部构型参照PUMA 机器人，全部为转动关节，保证了机器人的控制精度和灵活性。

关节机器人主要由底座、驱动臂构件、大臂构件、小臂构件、手腕构件和末端构件等6 部分组成；其5 个自由度分别为驱动臂构件的回转运动、大臂构件的俯仰运动、小臂构件的俯仰运动、手腕构件的俯仰运动和末端构件的回转运动。该机器人的基本结构如图1所示。关节机器人的运动由驱动臂构件、大臂构件和小臂构件的运动组合而成；手腕构件用于改变末端构件参考点的位置；末端构件用于改变末端执行器的姿态。

图1 关节机器人的本体结构Fig.1 Body structure of joint robot

1.2 建立D-H 坐标系

要实现对关节机器人的精确控制，需要对关节机器人系统进行动力学分析，在此采用拉格朗日法建立动力学方程进行动力学分析，选用经典的D-H法则建立数学模型。D-H 法则[10]是由Denavit和Hartenberg 在1955年提出一种通用的方法。为了表示各构件及系统的动能和重力势能，需要引用齐次坐标及4×4 齐次变换矩阵，通过依次变换可最终推导出末端执行构件相对于基坐标系的位姿（位置和姿态），从而建立机器人的动力学模型。

关节机器人有5 个转动关节，依据D-H 法则建立的简化空间坐标系如图2所示，得到的D-H 参数见表1。

图2 关节机器人的D-H 坐标系Fig.2 D-H coordinate system of joint robot

表1 关节机器人坐标变换的D-H 参数Tab.1 D-H parameters of joint-robot’s coordinate transformation

2 机器人动力学模型的建立

2.1 建立拉格朗日方程

考虑到关节机器人的具体结构，应用第二类拉格朗日方程[11]对该机器人进行分析，拉格朗日法比较适合分析相互约束下的多连杆运动。

拉格朗日函数L 定义为系统的动能Ek和重力势能Ep之差，即

系统的拉格朗日方程为

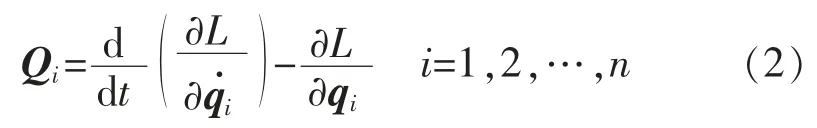
式中：qi，为系统的广义坐标和广义速度；Qi为广义坐标相对应的广义力矩。

2.2 建立动力学方程

设连杆i 上的质点v，其在基座坐标系中的径矢为vr，质量为vmi，vρi为连杆上的质点v 在i 坐标系中的点矢量，则该质点的动能vEki为

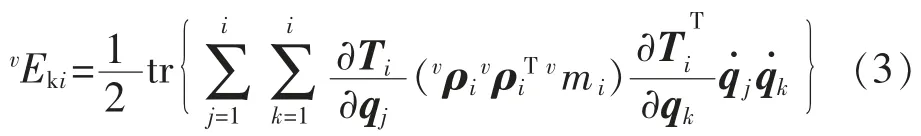
式中tr 为方阵的迹的运算符号。

连杆i 的总动能等于连杆i 上所有v 点的动能之和，即

其中

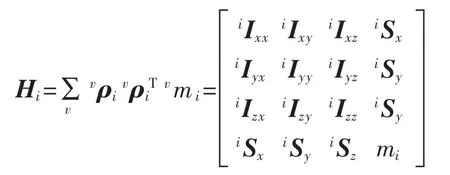
式中Hi为齐次坐标表示的惯量矩阵。则关节机器人各连杆的总动能为

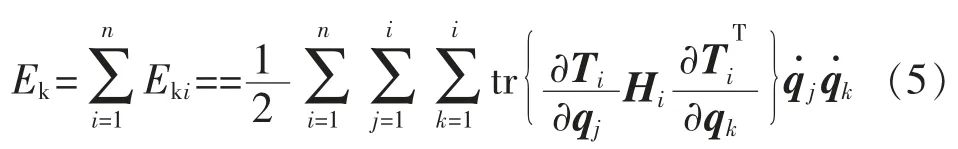
除了机器人连杆的动能外，还有机器人驱动各连杆运动的驱动元件的动能。这些部分的动能可以按各自的广义速度得出：

式中：Iai为驱动电机转子在广义坐标上的等效转动惯量；为驱动电机转子的广义速度。

机器人装置的总动能为各连杆的总动能和驱动元件的总动能之和，即

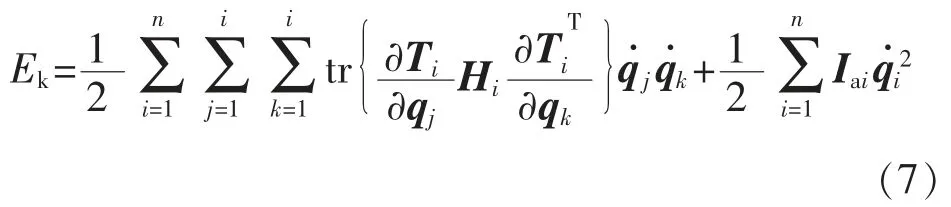
连杆i 的重力势能为

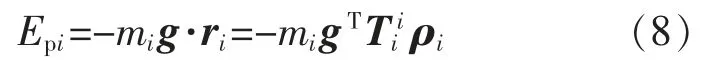
其中

式中g 为重力加速度矢量。

机器人各连杆总的重力势能Ep为

将式（7）和式（9）代入机器人装置的拉格朗日函数中，得

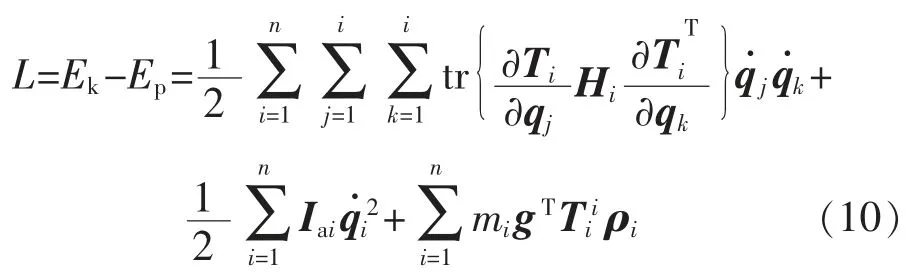
则该关节机器人装置的动力学方程为

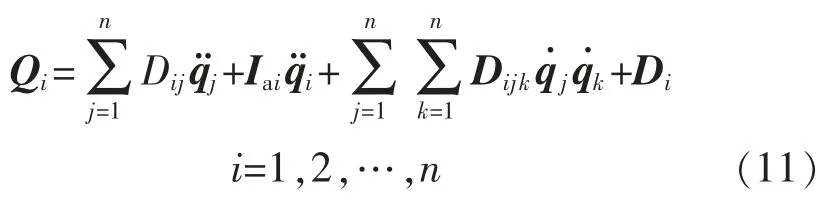
其中

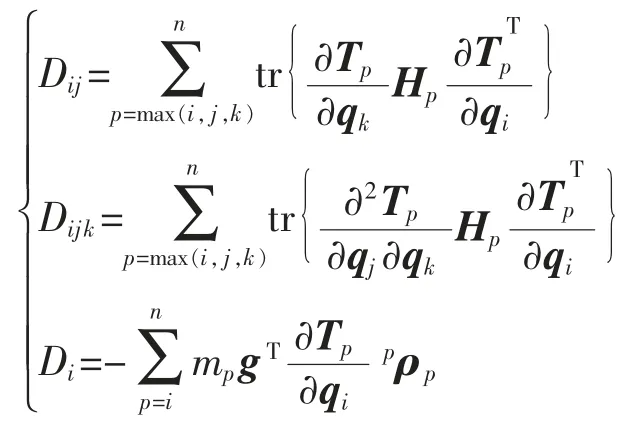
将关节机器人的相关参数代入动力学方程，可以得到关节机器人对应各关节处的驱动力矩值，见表2。

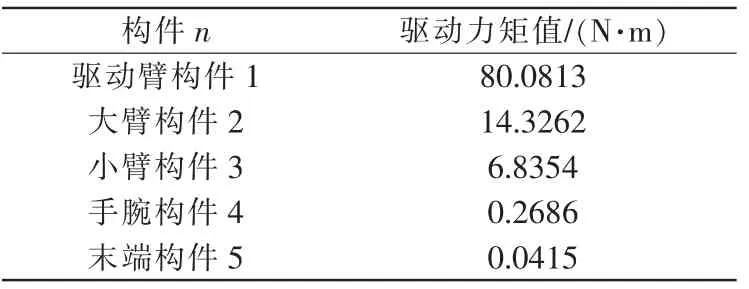
表2 各关节处的驱动力矩值Tab.2 Driving torque values at each joint

3 机器人的动力学仿真分析

3.1 ADAMS 仿真模型的建立

为验证通过动力学分析求解出的各关节理论驱动力矩值的正确性，需要应用ADAMS 对关节机器人进行动力学仿真分析。在将SolidWorks 三维实体模型导入到ADAMS 中之前，应对关节机器人模型进行简化，模型简化方法如下：

1） 在保证机构完成规定动作所需的运动副及约束条件下，去掉过约束；

2）在多个零件固定连接在一起时，可以简化为一个零件表示；

3）尽量简化模型的外形，保证能够清楚观察到机构的仿真动画。

遵循该简化方法，先将关节机器人模型实体进行简化，然后保存为Parasolid（*．x_t）格式，再导入到ADAMS 软件中；对模型分别进行属性修改，并对运动副添加约束和驱动等后处理后，建立好的虚拟样机仿真模型如图3所示。

图3 虚拟样机仿真模型Fig.3 Simulation model of virtual prototype

3.2 ADAMS 运动仿真分析

采用ADAMS 软件[12]进行动力学仿真分析，需要先给机器人各关节添加不同的运动驱动函数，进而控制机器人的关节运动，通过测量各关节的力矩就能得到输出预定运动时所需的驱动力矩。关节机器人在规定的工作范围之内可以有许多运动轨迹，不同的运动轨迹求出的关节峰值力矩也不尽相同。因此，有必要选取相对最优的运动轨迹，求解出的关节峰值力矩作为关节最大输出力矩。为此，应用MatLab Robotics Toolbox 工具箱调用jtraj 函数，对关节机器人进行轨迹规划，从而得到最优运动轨迹的运动数据[13-14]。

Spline 曲线是ADAMS 与外界进行数据交流的重要方法。通过将MatLab 中的运动数据导入到ADAMS中制成Spline 函数曲线，再利用函数CUBSPL（time，0，Spline_Name，0），将驱动函数添加到关节机器人各关节的驱动Motion 上，使得各关节按照特定的规律运动，从而实现对仿真模型运动的控制。

设置仿真时间为3 s，仿真步数为500步，得出关节机器人末端构件运动轨迹（如图4所示），末端构件在X，Y，Z 方向的速度和加速度曲线（如图5所示），以及各关节处的力矩变化曲线图（如图6所示）。

由图5 可见，关节机器人末端构件在X，Y，Z 方向的速度与加速度曲线平稳光滑，且ADAMS 仿真中关节机器人的运动轨迹与在MatLab 中规划的运动情况基本一致，证明了关节机器人结构和运动轨迹的正确性和合理性。

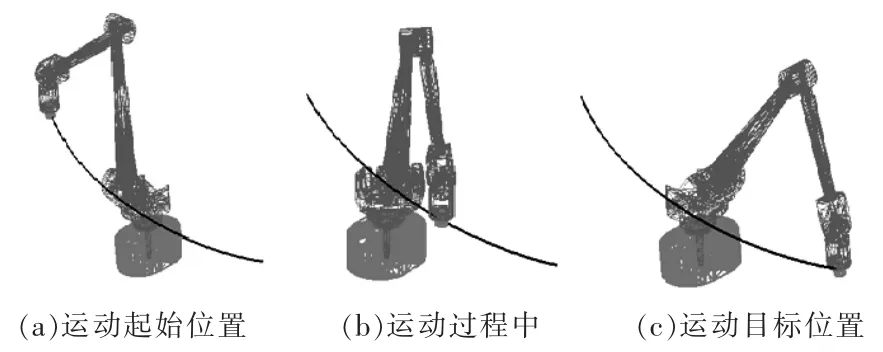
图4 末端构件的运动轨迹Fig.4 Movement path of the end member

图5 末端构件在X，Y，Z 方向的速度和加速度曲线Fig.5 Velocity and acceleration curve of the end member in the X，Y and Z directions

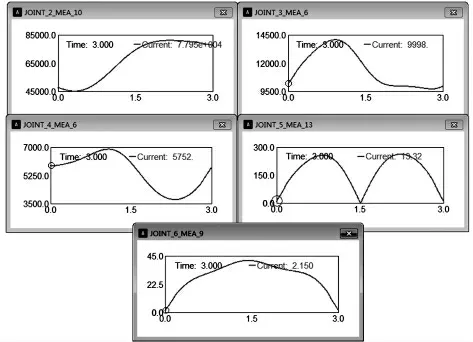
图6 各关节的力矩变化曲线Fig.6 Torque curve of each joint

由图6 可见关节机器人各关节处所需的最大输出力矩值，具体列于表3。通过对比关节机器人的动力学分析结果可知，关节机器人各关节处的最大输出力矩与所得到的理论驱动力矩值相差均在5%以内，可以证明动力学模型建立的正确性。

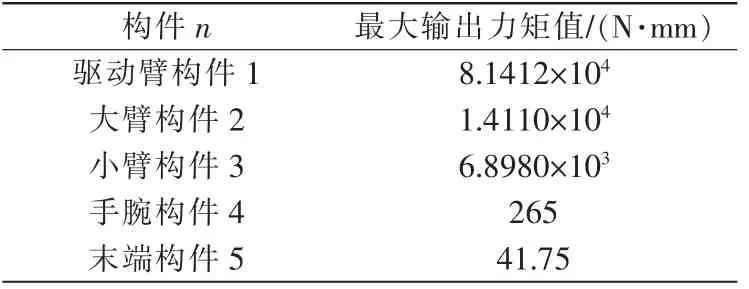
表3 各关节处的最大输出力矩值Tab.3 Maximum output torque values at each joint

4 结语

通过分析织物衣片自动对目与拼合的工作过程设计了关节机器人的本体结构，并应用拉格朗日法对关节机器人进行了动力学分析，得到了各关节对应的驱动力矩值。应用ADAMS 对关节机器人进行动力学仿真分析，得到了末端构件的运动轨迹、速度和加速度的变化曲线以及各关节的力矩变化情况。试验结果表明，ADAMS 中仿真模型的运动轨迹与MatLab 中规划的运动情况基本一致，以及测量出各关节的最大力矩值与理论驱动力矩值相差均在5%以内，从而证明动力学模型和轨迹规划的正确性，也为进一步完善机器人结构以及各关节电机、减速器的选型奠定基础。