含瓦斯煤渗透率演化模型和实验分析

祝 捷，唐 俊，王 琪，王全启，张 博，张 犇

(1.重庆大学 煤矿灾害动力学与控制国家重点实验室，重庆 400044; 2.中国矿业大学(北京) 力学与建筑工程学院，北京 100083)

煤矿开采或煤层气开发过程中，气体压力发生变化，与气体压力有关的煤层渗透率变化规律受到工业界和学术界的广泛关注。

林柏泉和周世宁[1]最早进行了瓦斯压力变化过程中煤样渗透性实验(实验围压2.45 MPa)，发现煤样渗透率随着瓦斯压力的增大而降低，后来许多学者的实验结果(实验围压为2.0～3.0 MPa)验证了林柏泉的实验结论[2-6]。王登科[7]和朱卓慧[8]等在较高应力条件下(实验围压、轴压分别为8.0和12.0 MPa)，测得不同气体压力下圆柱体型煤的渗透率随着瓦斯压力的增大而增大。张广洋[9]、曹树刚[10]和魏建平[11]等实验研究了不同应力条件下(实验围压和轴压为2～6 MPa)，瓦斯压力增大的煤样渗透率变化特征。实验数据表明，随瓦斯压力的增大，煤样渗透率先减小后增大。许江等[12]的实验表明瓦斯压力下降过程中型煤的渗透率先减小后增大(实验有效应力5.7 MPa)。由此可见煤样渗透率随着气体压力的变化趋势是多样的，渗透率演化特征与外部应力条件和煤样类型(原煤、型煤)有关。

瓦斯压力下降引起有效应力增大，煤体孔裂隙受压缩导致瓦斯流动通道减少;同时瓦斯压力下降促使瓦斯解吸和煤基质收缩，这导致煤体孔裂隙通道增多。气体解吸导致煤基质收缩被认为是导致煤渗透率发生变化的重要原因[13-14]。学者们在研究瓦斯解吸引起煤基质收缩的基础上[15]，将煤基质收缩的影响引入煤层渗透率的计算模型，研究了煤层气抽采降压时煤层渗透率变化规律[16-18]。SHI和DURUCAN把降压过程中渗透率由降转升的拐点对应的气体压力称为渗透率反弹气体压力，初始储层压力是否高于反弹气体压力，是导致渗透率呈现降低或者升高等不同变化趋势的重要原因[16]。

由于瓦斯抽采和煤层气开发过程中气体压力不断降低，且存在变形对煤层渗透率的影响[19]，笔者对降压条件下煤样的变形和渗透率进行了实验测试;考虑到实验条件下煤样的变形特征，构建了降压条件下的煤样渗透率演化模型，并结合不同应力和瓦斯压力条件下的煤样渗透性实验数据，验证了模型的正确性。

1 降压条件下的含瓦斯煤渗透性实验

1.1 实验方案和煤样制备

实验在重庆大学煤矿灾害动力学与控制国家重点试验室完成，实验设备采用含瓦斯煤热流固耦合三轴伺服渗流装置。试样为钻芯取样的圆柱体原煤(直径为50 mm、高为100 mm)，取自开滦矿区赵各庄煤矿9号煤层(取样深度1 084 m)，该煤层瓦斯含量为6.6～8.7 m3/t，超过了《我国防治煤与瓦斯突出规定》中突出危险煤层瓦斯含量临界值(8 m3/t)，煤层有煤与瓦斯突出危险。

煤样的渗透性实验在常温下进行，采取维持外部应力7.0 MPa、降低气体压力的方式。其中进口气体压力按照2.0，1.5，1.0，0.5，0.3 MPa逐级降低，出口气体压力为大气压(0.1 MPa)。具体实验步骤如下:在保证实验设备气密性的条件下，将实验轴压和围压设为7.0 MPa，对样品腔进行不少于2 h抽真空，之后通入规定压力的瓦斯气体，待煤样充分吸附瓦斯后打开出气口，测量出口气体的稳定流量，应变仪同时采集煤样的径向变形和轴向变形。之后关闭出气口，再次抽真空后，通入下一个预设压力值的瓦斯气体，充分吸附后测量出口气体流量和煤样变形，重复以上实验操作直到完成所有预定测试后，结束实验。

1.2 实验结果与分析

根据测量出口处气体流量Q(mL/s)，由式(1)计算得到煤样的渗透率k(10-15m2):

(1)

式中，pa为大气压，MPa;μ为流体动力黏度，MPa·s;L为煤样的长度，cm;A为煤样的横截面面积，cm2;p1，p2分别为进口气体压力和出口气体压力，MPa。

将进口气体压力为2.0 MPa设为初始状态，煤样对应有初始体应变为εV0，初始渗透率为k0。图1为进口气体压力p1从2.0 MPa降低至0.3 MPa，煤样渗透率变化系数k/k0、径向应变εr和轴向应变εz的实验结果。

由图1可知，实验煤样的渗透率变化特征不同。1号煤样k/k0实验点均在k/k0=1的基准线以上，这表明降压过程中渗透率逐步增大。气体压力p1降至0.3 MPa，渗透率为15.20×10-15m2，约为初始渗透率的2.9倍。2号和3号煤样k/k0最小值分别出现在进口气体压力1.0和1.5 MPa，可见随着气体压力的降低，渗透率先减小后增大，呈现出渗透率的“V”字形变化特征。进口气体压力p1降低至0.3 MPa时，2号和3号煤样渗透率分别为15.20×10-15和15.14×10-15m2，约为初始渗透率的1.9倍。

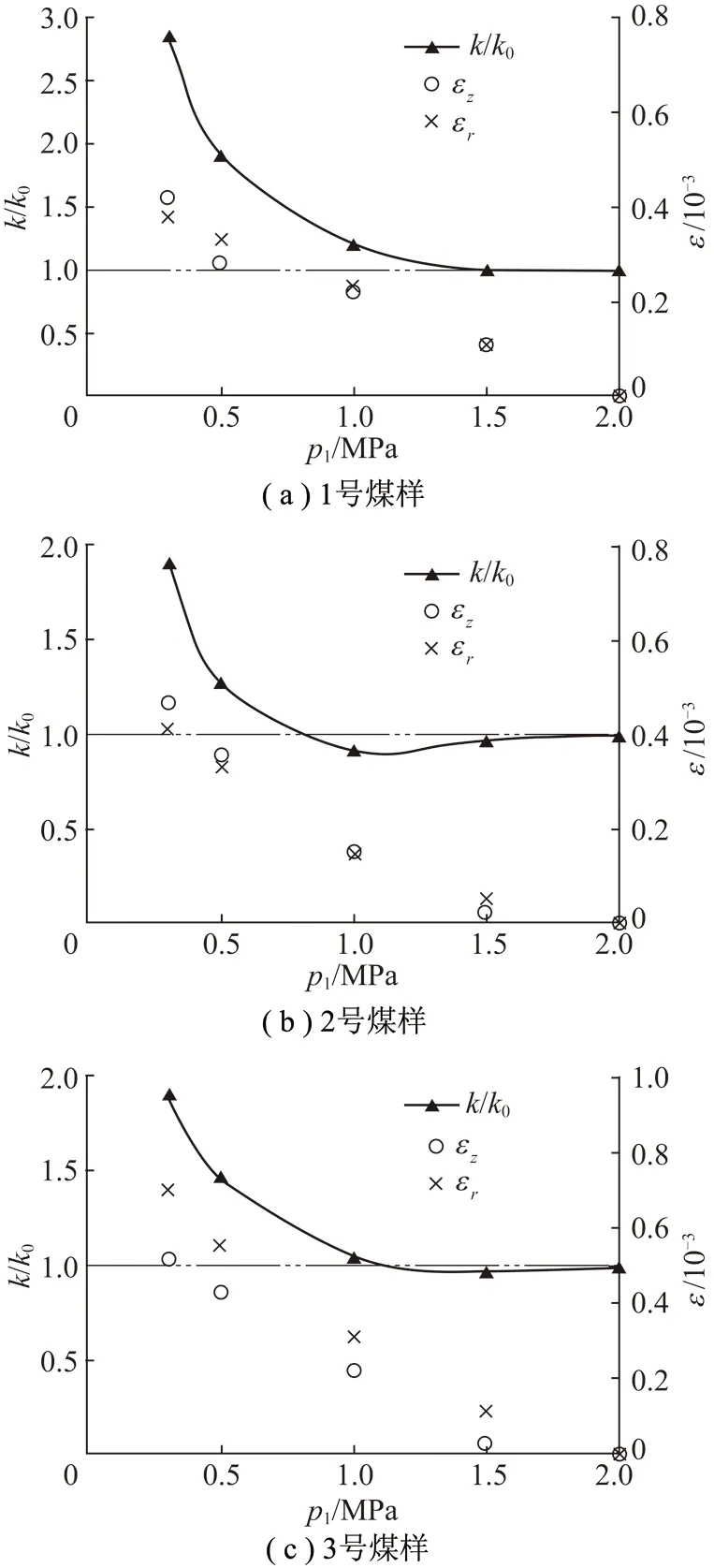
图1 煤样应变和渗透率实验结果Fig.1 Experimental curves of coal strain and permeability

实验结果还显示:随着瓦斯压力的降低，煤样的收缩变形逐渐增大。图1(a)中1号煤样径向应变εr和轴向应变εz接近，且与气体压力之间近似为线性关系。2号煤样径向应变εr和轴向应变εz接近，进口气体压力降为1.5 MPa时，煤样收缩变形很小，气体压力低于1.5 MPa，煤样应变随气体压力发生线性的变化。3号煤样径向应变εr大于轴向应变εz，径向应变与气体压力之间近似为线性关系，轴向应变εz在进口气体压力为1.5 MPa时变化很小，当气体压力低于1.5 MPa，轴向应变与气体压力之间保持线性的变化关系。

2 考虑煤体变形的渗透率模型

煤层渗透率k常被表述为与有效应力有关的指数函数[16]，即

k=k0exp(-3CfΔσ)

(2)

式中，Cf为裂隙体积压缩系数，MPa-1;Δσ为有效应力变化量，MPa;k0为初始渗透率，10-15m2。

SHI假定煤层仅发生一维应变，得到降压条件下的煤层渗透率[16]为

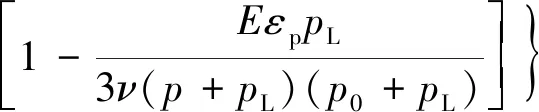
(3)

式中，E为煤的弹性模量，MPa;ν为泊松比;p0为初始储层压力，MPa;p为平均气体压力，MPa，p=(p1+p2)/2;εp为Langmuir最大吸附应变;pL为50%最大吸附应变对应的气体压力，MPa。

本文的实验结果表明煤样在径向和轴向均发生收缩变形，且两个方向的应变数值接近，显然不符合SHI提出的一维应变假定。为了分析本文实验得到的渗透率变化规律，需要考虑煤样的实际变形情况。

根据国内外学者建立的煤岩体渗透率模型[16-18]，假定煤样应力应变关系满足:

(4)

式中，G为剪切模量，MPa;λ为拉梅系数，MPa;δij为克罗内克符号;σij为应力分量，MPa;εij为应变分量;εV为煤样的体应变，εV=εz+2εr;εs为气体吸附解吸导致的煤样体应变，满足Langmuir方程[16]:

(5)

根据大多数煤样渗透性实验针对圆柱体煤样施加轴压和围压的实验条件，将式(4)写为

(6)

式中，σr和σz分别为径向应力和轴向应力，MPa。

假设实验过程中轴压和围压不变，进口气体压力变化，则Δσr=Δσz,式(6)可简化为

Δσ=Δσr=Δσz=K(ΔεV+Δεs)

(7)

式中，K为煤样的体积模量，K=E/3(1-2ν)。

将式(5)和(7)代入式(2)得到

(8)

式(8)表征了外部应力不变，气体压力改变过程中煤样产生三维应变条件下的渗透率变化规律。式(8)同时考虑了煤样吸附效应对渗透率的影响，因此渗透率的变化是气体压力作用和气体吸附解吸效应的叠加结果。

比较式(3)和式(8)发现，渗透率计算公式在形式上是不同的。式(3)是假定煤层仅发生一维应变条件下得到的[16]，式(8)是本文考虑煤样发生径向应变和轴向应变的条件下推导的。由此可见煤样或煤层的变形状态不同，其渗透率的变化特征也不相同。

将式(8)得到的煤样渗透率k表示为气体压力p的函数，即

k=f(p)=k0exp[-3Cff1(p)]

(9)

式中，f1(p)为气体压力p的函数:

对f1(p)求一阶和二阶导数得到

f1(p)的两阶导数f″1(p) 恒小于0，则f1(p)函数存在极大值。当f′1(p)=0,取得极大值，此时式(8)得到极小值，对应的气体压力pr为

(10)

该气体压力pr为反弹气体压力。式(10)表明煤样的体积模量K、与吸附效应有关的Langmuir系数εp和pL共同决定了pr的取值。体积模量K与吸附变形系数εp越大，pr越大。值得注意的是，pr的取值与煤样的外部应力以及内部的气体压力无关。

理论上讲，只有反弹气体压力pr>0，才可能观测到气体压力变化过程中煤样渗透率由降低转为升高的现象。由式(10)可知

(11)

则煤样体积模量K与Langmuir吸附常数εp，pL之间须满足:

(12)

由此可见，煤样的体积模量K>pL/εp，是实验测得渗透率出现“V”形变化的必要条件。

3 分析与讨论

根据煤样的吸附变形实验和单轴压缩实验结果，得到实验煤样的弹性模量E、泊松比ν以及吸附体应变的Langmuir系数εp和pL见表1，其中裂隙体积压缩系数Cf的取值参考了文献[16-17]的数据。

依据表1参数，本文计算了煤样的反弹气体压力。计算结果显示:3个煤样的反弹气体压力相差不大，数值在0.74～0.92 MPa，煤样渗透率的最小值出现在气体压力降低至初始气体压力的70%～88%，继续降低气体压力，煤样的渗透率由降转升。2号和3号煤样的实验结果验证了以上渗透率先减小后增大的变化特征。

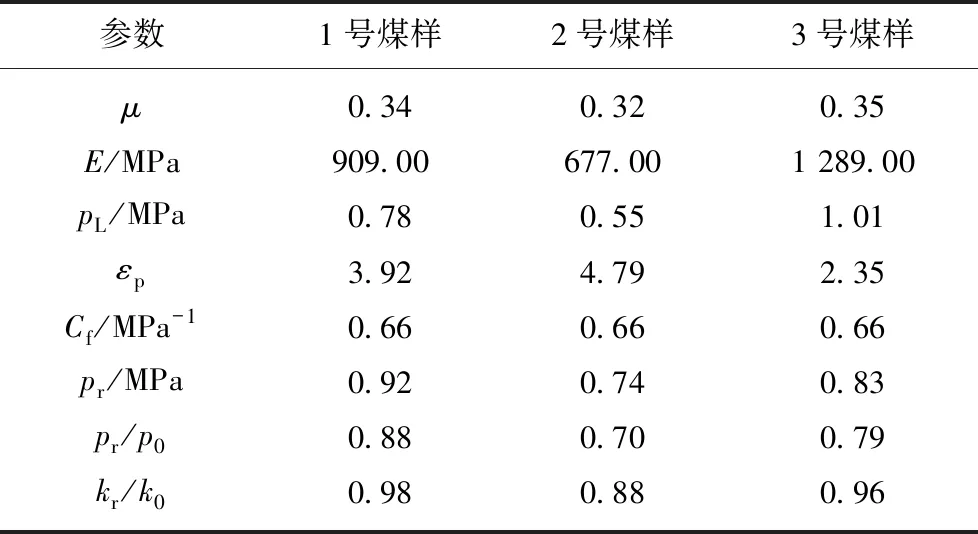
表1 煤样渗透率的基本计算参数Table 1 Parameters related to coal permeability

1号煤样理论上的反弹气体压力为0.92 MPa，对应的进口气体压力为1.74 MPa。1.74 MPa低于初始气体压力2.0 MPa，因此气体压力降低过程中，煤样渗透率的变化趋势理论上应为先降低后升高。为什么实验结果显示1号煤样渗透率的变化趋势是增大呢？图2显示了1号煤样测定渗透率的气体压力测点。按照本文模型算得进口压力为1.5 MPa时，渗透率与初始渗透率比值k/k0等于1;当进口压力低于1.5 MPa，对应的k/k0由1.21逐渐增大至2.81。理论计算显示实验测点对应的渗透率均不低于初始渗透率，这与实验数据反映的渗透率逐渐增大的变化趋势是一致的。由此可见实验选取的气体压力测点有限，测得降压过程中渗透率有可能出现增大或先减小后增大等多种变化趋势。

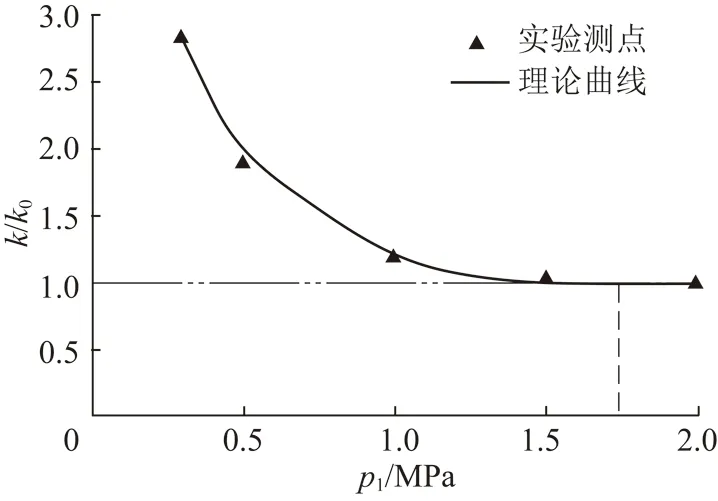
图2 1号煤样渗透率的理论值及实验测点Fig.2 Numerical results and measuring points of coal permeability for No.1 coal sample

依据表1的计算参数，依据SHI模型和本文模型算得煤样渗透率变化曲线如图3所示。由图3可知，本文模型得到的计算值更加接近实验数据。

图3 煤样渗透率的计算结果Fig.3 Computed results of coal permeability

表2是渗透率计算值与实验数据对比的误差分析结果。表2显示，本文模型计算结果的绝对误差、相对误差以及平方差和均低于SHI模型计算结果的对应值，其中本文模型的相对误差在8.9%之内，显著低于SHI模型的相对误差(19.7%～45.3%)。因此本文模型的计算结果与实验结果更加接近。

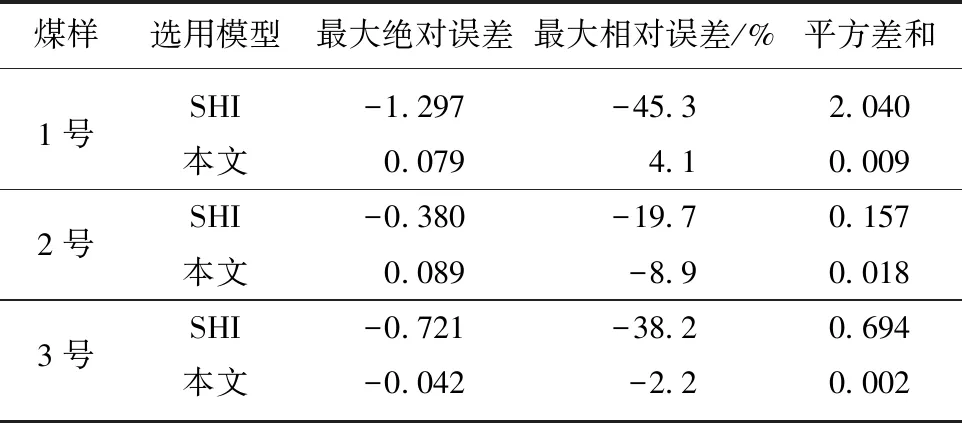
表2 煤样渗透率计算结果的误差分析Table 2 Error analysis of coal sample permeability

造成2种模型的计算结果存在较大差异的原因在于SHI模型与本文模型对煤样采用了不同的变形假设。SHI模型假设煤样仅发生一维应变，本文模型则考虑了煤样的轴向和径向变形。因此研究煤层或煤样的渗透率演化特征，合理考虑煤层或煤样实际变形状态是非常必要的。

为了进一步验证渗透率演化模型，结合参考文献[6,8,11]的实验数据，本文计算得到了渗透率随气体压力的变化曲线(图4)。实验测试的应力条件、煤样类型以及模型计算需要的参数见表3，其中弹性模量E和泊松比ν取自原参考文献;εp,pL和Cf原参考文献中未涉及，由作者根据相关文献[16-17,20]取值。

表3 前人实验结果对应的计算参数Table 3 Parameters in the predecessor’ experimental results

注:表中平均应力等于(2σr+σz)/3。

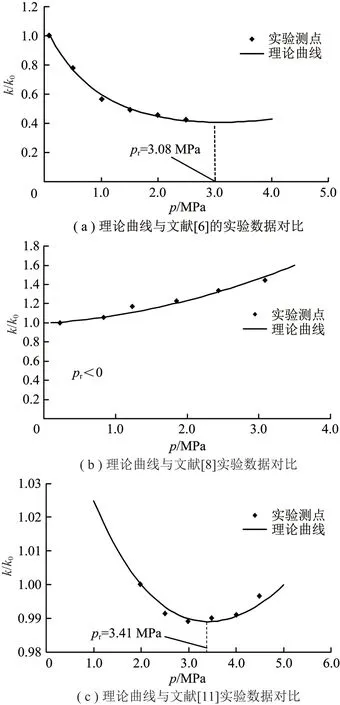
图4 模型结果与前人实验结果的对比Fig.4 Comparison of model results and the predecessor’s experimental data

图4显示，模型计算结果呈现出渗透率演化的不同趋势，且计算结果与相应文献的实验数据吻合。分析图4可知，实验测得煤样的渗透率表现为何种变化趋势，取决于反弹气体压力pr和实验气体压力的关系，具体如下:① 当pr≥pmax(实验测点中最大的气体压力值)时，渗透率随着气体压力增大而降低，如图4(a)所示;② 当pr≤pmin(实验测点中最小的气体压力值)时，渗透率随着气体压力增大而增大，如图4(b)所示;③ 当pmin

4 结 论

(1)实验数据显示，在恒定轴压和围压条件下，瓦斯压力降低过程中，煤样的收缩变形逐渐增大，渗透率的变化趋势为先减小后增加或者逐渐增大。渗透率回升对应的反弹气体压力小于1.0 MPa。

(2)构建的煤样渗透率演化模型，综合考虑了气体压力和吸附解吸作用的影响。通过对比模型计算结果与实验数据发现，本文模型比SHI模型的计算结果更接近实验数据。因此研究煤层或煤样的渗透率演化特征，考虑煤层或煤样实际变形状态是非常必要的。

(3)计算得到了气体压力变化过程中渗透率的不同变化趋势，且模型计算结果与前人实验数据吻合。研究表明，随着气体压力变化，煤样渗透率可以表现出不同的变化趋势(增大、减小或者“V”形)，这取决于反弹气体压力与实验气体压力之间的关系。