一种星敏感器安装误差自动化测量方法
2019-07-10陈伟雄王林郑涛马步川
陈伟雄 王林 郑涛 马步川

摘要:针星敏感器安装误差的精确标定,该文提出基于平台式惯性/星光组合导航系统中,星敏感器相对惯性坐标基准的安装误差自动化测量方法。首先基于光电自准直仪测量方式,建立安装误差测量的数学模型,并通过仿真验证模型的有效性。开发一套自动化测试系统,利用高精度的光电测角仪模拟星光,将星敏感器主光轴对准星点,输出星点坐标信息,自准直儀测量标准六面体的姿态,通过与星敏感器坐标对比和软件自动解算得到星敏感器相对标准六面体的安装误差。试验数据能达到5′′内的测试稳定精度,证明该方法可准确测量出星敏感器的安装误差,且测试稳定性好,已应用于工程精密测量。
关键词:惯性/星光组合导航系统;星敏感器;安装误差标定;光电自动化测量
中图分类号:V448.22
文献标志码:A
文章编号:1674–5124(2019)02–0111–05
0 引言
在惯性/星光组合导航系统中,星敏感器作为重要测量单元,其测量恒星姿态的精度可达角秒级,但因当前星敏感器安装误差的测试方法误差较大,导致安装误差的测量结果可达角分级。据此带来的测量误差远高于星敏感器自身的随机测量误差,严重影响星敏感器的测量信息[1]。
在平台式惯性/星光组合导航系统中,星敏感器以标准六面体为基准安装在惯性系统中,基于惯性测量坐标系,依靠惯性系统使光轴视线稳定在惯性空间[2]。目前主要通过三坐标机或自准直仪测量星敏感器自带六面体和标准六面体之间的相对位置表示星敏感器安装误差[3],但测试结果误差较大,原因有:1)星敏感器自带六面体受表面加工工艺限制,精度较低;同时六面体安装不稳定,在长期测试过程中因应力释放易产生精度漂移,测试数据稳定性较差;2)两种六面体的位置测量,需使用高精度平面镜作位置基准,存在基准传递过程,且平面镜误差不可测,会引入系统误差;3)所使用的自准直仪为目视式,需通过人眼瞄准,不同人员测试结果存在明显差异,且仪器分辨率约在10′′左右[4],精度较低。
由于上述测试方法受六面体表面加工精度、六面体装配精度、仪器调平精度、基准传递以及人工操作不确定性等因素的影响,测试结果会产生20′′~50′′的误差,使星敏感器测量精度降低。因此,需要开展高精度的安装误差测试方法研究。
1 星敏感器安装误差坐标涵义
平台式惯性/星光组合导航系统使用星敏感器实现惯性+天文复合导航[5],星敏感器以主光轴上仰8°的方式安装在惯性系统中,安装精度要求高。惯性坐标基准XGYGZG(由标准六面体确定)和星敏感器坐标基准XSYSZS(星敏感器的主光轴为YS轴)的相对位置如图1所示。
星敏感器安装误差直接影响复合导航的精度,其中θX、θZ将1∶1影响天文方位修正角,而θY值的影响是该误差的余弦乘以星敏感器的输出。以上误差属于系统误差,可在方位计算时予以修正,以保证导航系统的制导精度[6]。
2 误差模型创建
惯性/星光组合导航系统建立的惯性坐标系是以标准六面体(表面精度可达3′′)为基准,星敏感器的安装误差也是相对标准六面体而言。因此,在测量安装误差时,要对星敏感器和标准六面体的相对位置进行测量。
本文采用光电自准直仪进行自动测量。但在实际测量过程中,当被测目标处于不同的摆放位置时,光电自准直仪测量各个方向上的角度偏差也会具有不同的误差计算方法[7]。
2.1 基于不水平度的角度偏差模型
由于星敏感器以主光轴上仰8°的方式安装在惯性系统中,若标准六面体在水平方向上的安装存在一定偏差,测试结果会因存在仰角而产生测量误差[8],因此需要对标准六面体的不水平度进行测量和校准。
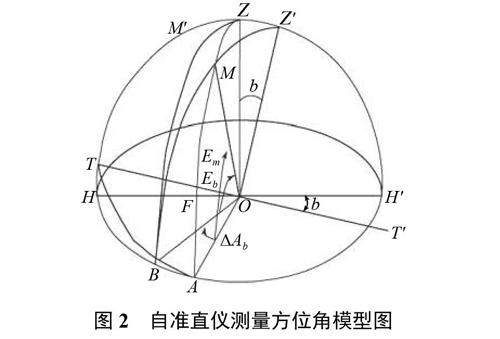
现针对不水平度产生的测量误差建立数学模型。如图2所示,图中M为目标,OZ为垂直轴,HH'为理想水平轴,TT'为实际水平轴,OA为对准轴。
若水平轴不存在倾斜情况,水平轴HH′应平行于水平面,对准轴连结形成的经过目标M的曲线弧为AZ,且大圆弧面AZO垂直于水平轴HH′;若水平轴在水平面上存在倾斜情况时,水平轴由HH′变为TT′,此时在面HZH′内作OZ′与TT′相互垂直,对准轴连接形成的经过目标M的曲线弧为BZ′。定义水平轴线的不水平误差为∠TOH′=∠ZOZ′=b,那么∠AOB就成为水平轴存在倾斜情况时造成的方位偏差,记作?Ab,若水平轴不存在倾斜情况时目标M的俯仰
角为∠AOM,记作∠AOM=Em;若水平轴存在倾斜情况时目标M的俯仰角为∠BOM,记作∠BOM=Eb。
在球面三角形ZBM中,按照球面余切定理可得:
因为∠BOZ=90°,∠MOZ=90°-Em,∠ZBM≈b,∠AOB=∠BZM=?Ab,则:
一般情况下b、?Ab的值很小,将式(3)按照泰勒级数展开,并取一阶近似得:
式(4)表明,水平轴的不水平度偏差影响方位测角的精度偏差值与被测目标俯仰角的正切成线性关系,若俯仰角越大,方位角的角度偏差值就越大[9]。
2.2 斜置状态下的方位偏差模型
由于星敏感器以主光轴上仰8°的方式安装在惯性系统中,为对准星敏感器光轴,自准直仪需要下倾8°进行角度测量。按照此种方式测得的方位偏差需经过余弦转化得到星敏感器在水平方向的实际方位偏差,具体见图3。
设星敏感器的理想安装位置为ST1,实际安装位置为ST2,∠BCA=∠BCS=90°。α′为自准直仪测得星敏感器在俯仰8°方向的方位偏差,α为方位偏差α′在水平面方向的投影,即实际方位偏差。根据位置关系可得:
所以,
′·
因为方位偏差α、α均为微小角度,根据高阶无穷小,可近似为tanα≈α,tanα′≈α′。故由于俯仰8°引起的实际方位偏差为
2.3 仿真分析
按照上述建立的误差数学模型,根据台体组件的实际装配精度,通过Matlab软件对误差数学模型进行仿真。目前标准六面体的安装精度(平行度、垂直度)在±5′′范围内,对b在–10′′~10′′、Em在1°~10°、α′在–10′′~10′′的范围内,进行公式仿真,结果如图4、图5所示。
由图可知,当被测目标的不水平度為5′′、俯仰角度值为8°时,其方位角会产生0.7′′的偏差;当被测目标在斜置状态下的方位角为1′′时,实际方位角会产生1′′的偏差;当被测目标在斜置状态下的方位角为10′′时,实际方位角会产生10.1′′的偏差。对于精度要求高的导航系统,上述误差不可避免[10]。
3 安装误差测试
本文研究直接测量星敏感器光轴代替测量其自带六面体的安装误差测试方法,它既需要仪器对准星敏感器光轴进行测量,还能模拟星点坐标。因此,采用集自准直/星模拟器功能于一体的光电测角仪,同时由于星敏感器特殊的安装方式,测试过程中光电测角仪的光轴需要水平向下倾斜8°安装。因为装配过程不涉及星敏感器滚动方向的安装误差[11],所以只针对星敏感器绕方位、俯仰轴方向的安装误差测量方法开展研究。
3.1 测试原理
测试时以标准体为基准,如图6所示,AX代表光电测角仪,A1、A2代表光电自准直仪。光电自准直仪、光电测角仪对标准体建立初始零位姿态后,再分别对准台体上的标准六面体、星敏感器,根据测试结果的差值和星敏感器的输出,就可以得到星敏感器坐标系S在标准六面体坐标系OTXTYTZT下表达式S|T的数学模型。
3.2 测试方法
完成设备的粗校准后,开始进行测试。标准体上的基准平面镜、基准六面体与星敏感器光轴、台体的标准六面体空间位置保持一致。测试光路结构如图7所示,测量时,首先将光电自准直仪、光电测角仪分别对准标准体上相对应的反光面,标定其相对标准体的姿态,完成校零操作。然后将标准体移出,将被测台体移入,光电自准直仪对准标准六面体:1#、2#光电自准直仪测量标准六面体X面、Z面的姿态;光电测角仪发出与其测量光轴同轴的模拟星光,星敏感器对准模拟星光后测量它相对光电测角仪的姿态,完成测量操作。
3.3 结果计算
根据校零与测量操作中1#、2#光电自准直仪、
光电测角仪、星敏感器的输出,基于2.1、2.2中建立的误差模型,按照下式可解算出星敏感器相对标准六面体的方位偏差θY和俯仰偏差θZ:
式中:GH0、GH——光电测角仪方位方向的零位值、测量值;
GV0、GV——光电测角仪俯仰方向的零位值、测量值;
Z1H0、Z1H——1#自准直仪方位方向的零位值、测量值;
Z1V0、Z1V——1#自准直仪俯仰方向的零位值、测量值;
Z20、Z2——2#自准直仪俯仰方向的零位值、测量值;
XY0、XZ0——星敏感器坐标值;
θY0、θZ0——标准体零位。
θZ的计算中增加上仰8°的安装补偿。
4 试验数据
针对仪器测量的数据,利用LabVIEW开发测试软件对硬件系统进行数据采集,经过滤波处理后计算结果,并将结果显示在计算机界面上,实现安装误差的自动解算,软件界面如图8所示。
按照3.2中的测试方法,对7套台体的星敏感器安装误差进行重复测试,以验证系统的测试精度,选取结果如表1所示。从表中数据可以看出,θY、θZ的测量结果极差最大分别只有3.56"和3.59"。为充分验证该方法所测数据的有效性,对其中某一台体组件进行一个月的长期稳定性测试,具体结果见图9。
从图中可以看出,前期测试数据变化稍大,这是由于星敏感器在测试初期,装配应力不稳定;随着长时间放置,其装配应力逐渐释放[12],安装误差的测试结果也趋于稳定,且变化幅度能稳定在5”以内。
5 结束语
该研究基于平台式惯性/星光组合导航系统,提出星敏感器安装误差的自动化测量方法,按照测量原理,设计光路系统,并应用LabVIEW开发测试软件,对设备输出信号、数据进行采集和处理,实现安装误差的快速自动测试。经过试验数据分析,证明该测试方法所测得的结果准确、稳定性好,能满足工程测量需求。此外,星敏感器的测量也会受环境温度等因素影响[13],后续将开展模型建立和误差分析的研究工作,进一步提高系统测量精度。
参考文献
[1]王宏力,何贻洋,陆敬辉,等.星敏感器安装误差的三位置法
地面标定方法[J].红外与激光工程,2016,45(11):320-325.[2]王常虹,夏刚,孟倩.平台式惯性/星光组合系统斜置对准方
法[J].导弹与航天运载技术,2011(1):14-17.
[3]毛玉良,代洁,杨叶,等.单星模双位置星惯组合安装误差标定技术[C]//中国惯性技术学会第七届学术年会论文集,2015.
[4]苏力.光电自准直小角度测量系统设计[D].西安:西安理工大学,2007.
[5]谭汉清,刘垒.惯性/星光组合导航技术综述[J].飞航导弹,2008(5):44-51.
[6]陈伟雄,王林,郑涛,等.惯性平台中星敏感器安装误差标定方法研究[J].导航与控制,2017,16(5):71-75.
[7]陈颖,张学典,逯兴莲,等.自准直仪的现状与发展趋势[J].光机电信息,2011,28(1):6-9.
[8]司高潞,马步川,郑涛,等.棱镜组件安装误差自动化标定方法研究[J].导航与控制,2016,15(5):100-103.
[9]田留德,刘朝晖,赵建科,等.三轴误差对光电经纬仪测角的影响[J].红外与激光工程,2013,45(11):192-197.
[10]张辉,田宏,袁家虎,等.星敏感器参数标定及误差补偿[J].光电工程,2005(9):1-4.
[11]王融,熊智,刘建业,等.一种星敏感器安装误差标定模型仿真研究[J].系统仿真技术,2013,9(4):288-291.
[12]李留建,王明海,许立军,等.单星方案确定平台误差角研究[J].弹箭与制导学报,2009,29(6):41-44.
[13]刘海波,谭吉春,郝云彩,等.环境温度对星敏感器测量精度的影响[J].光电工程,2008,35(12):40-44.
