P波粲偶素衰变到矢量介子的强子矩阵元修正

杨秀德，张远强

（1.遵义师范学院物理与电子科学学院，贵州遵义563006；2.西南大学材料与能源学部，重庆400715）

1 S矩阵元展开过程

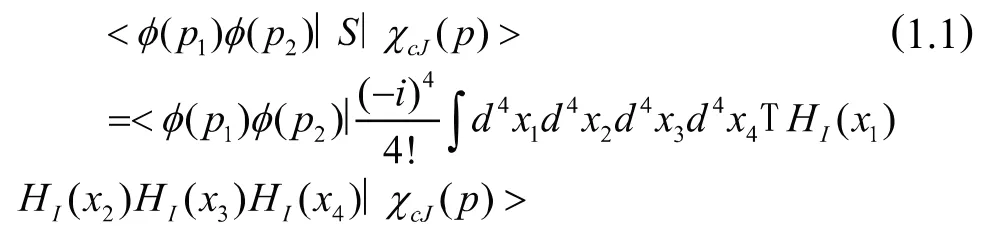
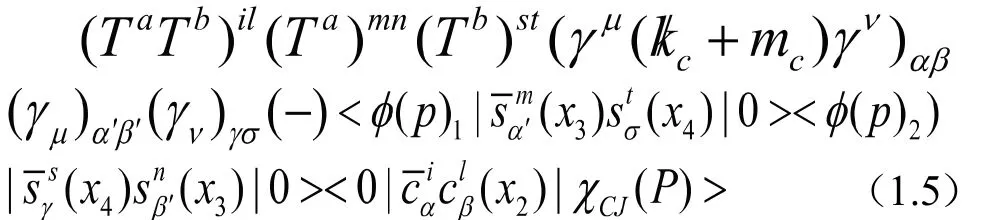
在上式中将矩阵元的颜色指标进行收缩后，利用Fierz恒等式

将强子矩阵元展开，因为研究的末态为矢量介子，所以其中有贡献的部分为四项。对于初态粒子的矩阵元我们采用非相对论下的零点波函进行处理，对于末态矢量介子采用强子矩阵元不同twist光锥分布振幅展开。但是，强子矩阵元的分布振幅展开在一般共形场论下有分母项和，不能对它像赝标介子一样进行处理[1]，因此需要对矢量介子的强子矩阵元光锥分布振幅进行重新研究。

2 分布振幅

首先要介绍几个类光锥矢量，它们是由介子四动量P和介子极化矢量构成的P和x。在P和z→x的情况满足以下关系[2]

在这个基础上来展开矢量介子强子矩阵元的分布振幅。我们以矩阵元关于Fierz恒等式展开后得到的项矩阵元为例来说明如何重新处理矢量介子强子矩阵元的分布振幅。根据文献[2]可以给出这部分一般共形场论下矩阵元的形式：

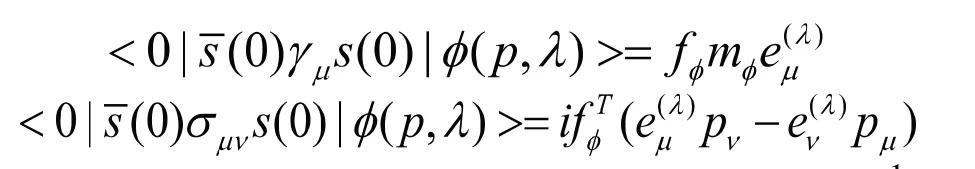
其中为twist-2分布振幅，为twist-3分布振幅，h3为twist-4分布振幅。为衰变常数，它们分别由来定义[2]。很明显在（2.1）中存在分母项和，因此需要对矩阵元进行处理。首先我们将代入，考虑化简后得到：

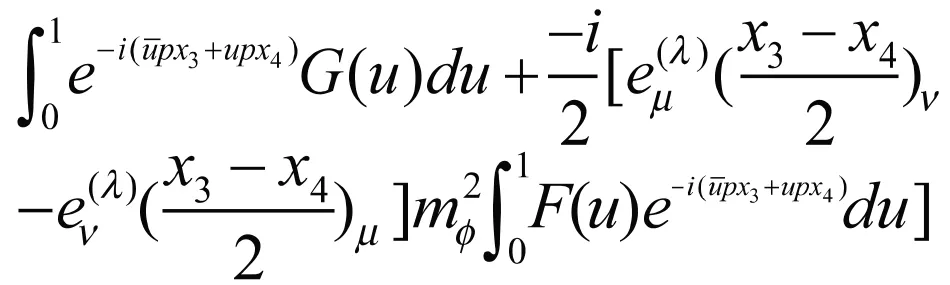
3 小结

本文通过分部积分和时空平移处理了的矢量介子强子矩阵元展开，消除了在一般共形场论下矢量介子强子矩阵元展开中存在的分母项，再通过时空平移将共形场论下的矢量介子强子矩阵元变化从而得到为我们计算衰变所需要的末态矢量介子强子矩阵元