动车组运用维修间隔优化方法的研究

姜 陈，周 斌，谢名源

(中国铁路上海局集团有限公司高铁运维技术中心，上海 201812)

1 动车组运用维修周期优化背景

1.1 动车组运用维修现状

我国动车组目前实行的是“计划预防修为主、事后维修补充”的维修体制，维修周期采用以走行公里周期为主、时间周期为辅的模式。我国动车组修程共分为五级，其中一、二级检修为运用检修，三、四、五级检修为高级检修，各级修程实施周期如表1所示[1]。

1.2 动车组现行维修体制存在的不足

(1)维修不足。简单地按照固定周期进行维修已无法防止功能故障的发生。同时，由于设备的个体性差异实际存在，制定维修周期间隔时考虑的风险失效概率不可能覆盖所有个体，所以计划预防修体制必然存在维修不足的问题。

(2)过度维修。由于安全性在动车组运用维修中占据着十分重要的位置，故动车组设备维修间隔制定得偏于保守，以保证足够低的失效概率。所以，对于大部分的动车组部件来说，在计划预防修体制下，均存在一定程度的过度维修。过度维修会带来一系列的问题，主要包括引发次生灾害、造成资源浪费和运用效率低等问题，对安全性而言，增加了安全隐患，对经济性而言，降低了企业的经济效益[2]。

2 现阶段维修间隔研究主要方法简介

2.1 应用数学模型确定维修间隔

应用数学模型确定预防维修的维修间隔存在诸多的应用场景，如目视检查、维护保养、定期拆修(报废)等均存在不同的数学模型，但在使用数学模型确定维修间隔时，需要在项目的故障规律和设计指标(如可靠性、经济性、安全性、可用度等)已知的前提下进行，不同维修内容在不同设计指标下的数学模型较多，在此不一一列举[3]。

2.2 应用CBR方法确定维修间隔

应用CBR方法确定维修间隔时，核心思想是在把相似的案例选择出来之后(常用基于GNN的案例选择方法)，认为目标问题和案例之间的相似就是问题间隔值和案例间隔值之间的相似，因此解析属性相似度公式就可以求出目标问题的间隔值，具体步骤如下。

(1)

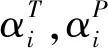
(2)确定综合相似度S(T，Pj)

(2)

式中，ω表示相似度阈值，用于调整选择的案例数量。

(3)确定维修间隔I

(3)

在动车组运用维修领域，因相似案例的间隔值均是统一规定的且不同车型之间存在着巨大的差异，所以应用CBR方法确定动车组运用维修间隔时，不能科学地反映维修任务真实的维修间隔。

2.3 基于MIDOT确定维修间隔

目前波音公司在787飞机维修大纲制订中采用MIDOT(maintenance interval determination and opti-mization tool)系统，以实时服务的数据为基础，辅助工作组完成维修大纲系统部分的维修间隔确定和优化。

MIDOT使用航空公司运营服务中可靠性数据库(ISDP)收集的数据，在确定组件维修任务的时间间隔时，通过可靠性分析，得到该组件故障率曲线，进而得到有效的任务间隔。MIDOT分析流程及实施步骤如图1所示[5-6]。

图1 MIDOT分析流程及实施步骤

波音公司的MIDOT方法在行业内比较先进，值得我们去学习和借鉴。但是，该方法关键参数是建立在波音原型机大量的运营数据基础之上的，且波音公司未对外公开MIDOT方法的关键技术和具体方法，对于我国动车组的运用维修而言，缺少此类关键的参数数据。

3 动车组运用维修间隔优化方法

3.1 动车组运用维修的主要维修方式

目前动车组运用维修主要以计划预防修和事后维修为主，随着动车组车载信息感知网络、车地通信技术以及先进的诊断与预测等技术手段的不断发展和运用，未来逐步发展为“计划预防修为主、视情维修辅助、事后维修补充”的维修方式，具体维修内容如图2所示。

图2 动车组运用维修内容

3.2 不同维修方式下的可靠度曲线

针对上述维修内容，维修活动对设备的可靠度会产生不同程度的影响，按不同的维修方式分，主要有如下4种。

(1)目视检查、功能测试、性能检测——不改变动车组部件状态的维修方式。对于目视检查、功能测试以及性能检测等维修活动而言，部件的状态不因维修活动的进行而改变，可靠度曲线变化情况如图3所示。

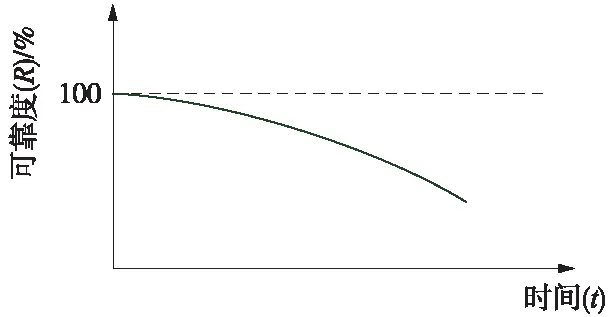
图3 采用不改变部件状态的维修方式的设备可靠度变化曲线

(2)小故障处理——最小维修方式。在设备发生故障时，对其实施维修策略，令其恢复原有的功能，使设备在维修前后的可靠度保持一致即为最小维修，亦称之为恢复如旧。最小维修方式是维修小故障的最佳方式。采用最小维修方式的设备可靠度变化情况如图4所示。

图4 采用最小维修方式的设备可靠度变化曲线

(3)故障处理(部件更换)——完全维修方式。在设备发生故障时，通过实施维修来恢复设备的功能，维修后设备如同新出厂一样，这种维修方式也称为修复如新，对应动车组维修中的故障部件更换处理。采用完全维修方式的设备可靠度变化情况如图5所示。

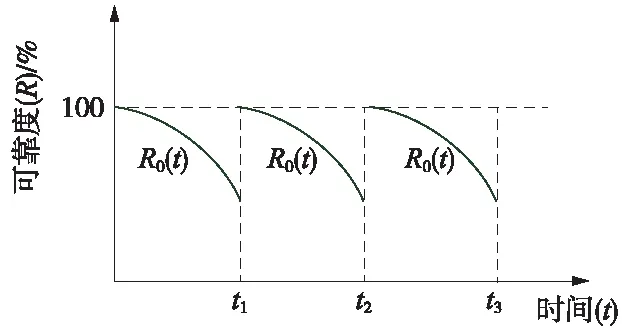
图5 采用完全维修方式的设备可靠度变化曲线

(4)维护保养——不完全维修方式。在设备性能下降或发生故障后对设备进行维修，经过维修后，设备性能介于完全维修与最小维修之间。这种维修方式称为不完全维修。实施不完全维修策略，可以有效提高设备的性能和可靠性。不完全维修后设备的可靠性低于完全维修，高于最小维修，采用不完全维修方式的设备可靠度变化情况如图6所示。

图6 采用不完全维修方式的设备可靠度变化曲线

3.3 动车组运用维修间隔优化策略

不同维修方式下的维修间隔优化，应采取不同的维修策略[7-11]。

(1)目视检查、功能测试、性能检测等维修方式，或以最小维修方式进行的小故障处理，因其维修活动不改变动车组部件状态或恢复如旧，部件可靠度曲线可以反映部件的一般失效规律，对于此类部件的维修周期，适合使用基于可靠性理论的数学模型来确定维修间隔。

(2)对于部件更换的完全维修方式，在故障数据处理上可通过采用类似寿命试验的处理方法，同样可以使用基于可靠性理论的数学模型来确定维修间隔。

(3)对于采用维护保养类不完全维修方式的部件，可靠度曲线的漂移存在一定的不确定性，很难评估维修活动对部件可靠度的影响，对于此类部件，确定其科学的维修间隔应当基于全寿命试验(调查试验)来确定。

同样，在处理动车组某些故障模式的故障数据时发现(尤其对于部分关键部件)，因部件较高的可靠性水平或由于保守的维修策略，实际运用过程中故障数据很少或者根本未发生过故障，对于此类部件，应当基于全寿命试验(调查试验)来确定。

(4)随着动车组状态信息感知网络的完善、高速车地通信技术以及诊断和预测技术的发展，应当尽可能地对具备条件的部件，通过部件的状态评估检查潜在故障，以此采取措施预防功能故障，或者是避免功能性故障的后果，实现视情维修。

本文仅讨论上述第(1)、第(2)两种情况下的维修间隔的确定方法。

3.4 确定动车组运用维修间隔优化流程

经过对现阶段国内外航空、轨道交通领域主要的维修间隔理论的研究，以及对动车组运用维修的特点和维修间隔优化策略的分析，总结出了一套确定动车组运用维修间隔优化的流程，具体流程和步骤如图7所示。

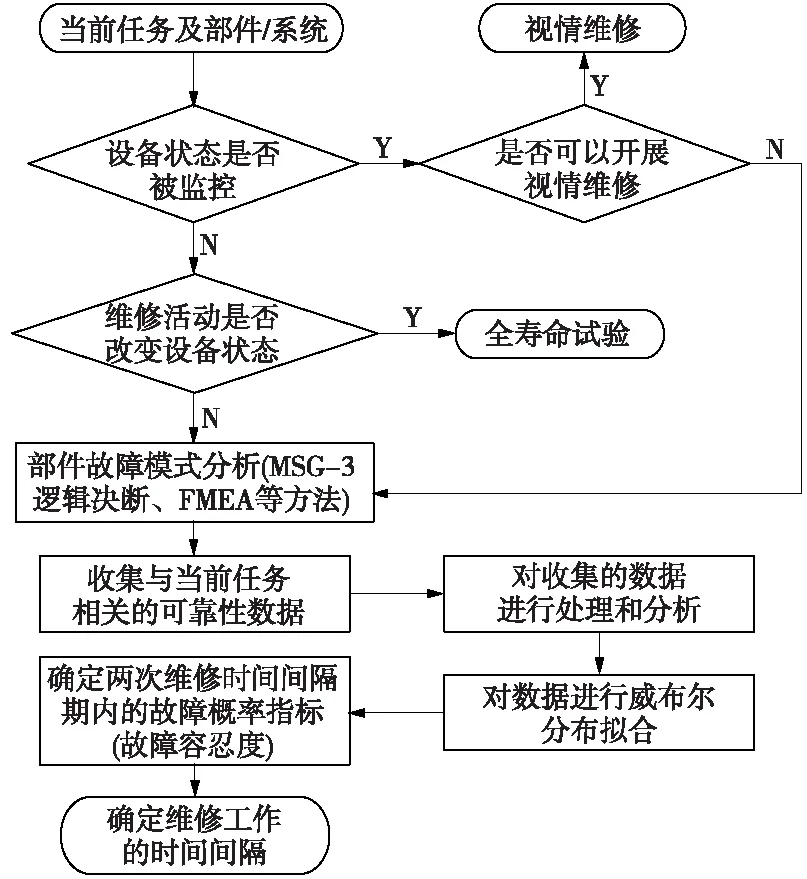
图7 动车组运用维修间隔优化流程及步骤

3.5 动车组故障数据(可靠性数据)的处理

在动车组运用维修间隔优化流程中，最关键和重要的部分是对收集的故障数据进行处理和分析。本文主要讨论运用生存分析与可靠性理论处理和分析故障数据的方法[12-13]。

(1)动车组运用故障数据的特点

故障数据是实际运用中产生的，在以n个动车组部件为样本对动车组故障进行观测和统计时，得到的故障数据如下。

①寿终数据(又叫完全寿命数据)：t1，t2，…，tn1，即故障发生或寿命终结的确切数据。

②“右删失”数据：t+n1+1，…，t+n1+n2。

在工程上和医学上有一种情形是事先规定试验或观测的截止时间L。有的个体在试验或观测截止时并未发生故障或寿命并未终结，这时称该个体的寿命在L被截尾，同时把这种情况归于“右删失”。动车组故障数据统计一般为统计截止某个时间或走行里程时的故障发生情况，对于大部分部件而言，由于较高的可靠性，此时并未发生故障或失效，故动车组多以右删失数据为主。

③区间型数据：[t(1)n1+n2+I，t(2)n1+n2+i](i=1，2，…，n3)。

即个体部件的确切故障时间或确切寿命t未知，只知道其在两次检修t(1)与t(2)之间(即t(1)≤t≤t(2))，这时称[t(1)，t(2)]是个体故障或寿命的区间型数据。动车组故障存在区间型数据，但故障发生的里程区间与故障发现时车组的里程数据相比可以忽略不计，在此可以将区间型数据等同于寿终数据处理。

以上n1+n2+n3=n，0≤ni≤n，i=1，2，3。

(2)生存分析与可靠性在动车组故障数据处理上的应用

由于删失数据的引入，使得动车组故障数据的处理变得较为复杂，但一般的统计学方法讨论的都是数据为完全寿命数据的情形(相当于n1=n，n2+n3=0的情形)，故本文使用生存分析对动车组故障数据进行处理分析，因为生存分析的一大特点就是讨论含有删失数据或区间型数据的情况。

对于不改变动车组部件状态的维修活动来说，未发现故障时不需要采取任何措施，当发现故障时，一般对其最小可换单元进行更换，保证动车组的正常运用。对所有参与统计的部件进行观测，观测原理类似于常规寿命试验中的“随机右截尾试验”，即从分布函数为F(x，θ)的总体中，随机抽取n个个体进行寿命试验或观测，对于每个试验或观测的个体，都有个截尾时间与之对应，对n个个体而言就会得到n个观测值。

在利用生存分析与可靠性处理动车组故障数据时，除了需要对动车组数据的“删失机制”有所认识外，还应对总体样本的寿命X的特征规律(分布类型)有所认识。在工程上，常用的故障分布主要有：指数分布、正态分布、对数正态分布、威布尔分布等，其中威布尔分布是维修性领域里使用较为广泛的分布模型，威布尔分布可以用来对机械设备中许多通用的零部件(如走行部的齿轮和轴承、密封件、继电器等)进行可靠性分析与评价[14-16]，本文主要以寿命特征规律符合威布尔分布的动车组部件为例，介绍维修间隔的优化方法。

(3)威布尔分布

两参数威布尔分布的失效分布函数为

(4)

其中，η，β0；η和β分别为函数的尺度参数和形状参数。

其可靠度函数为

(5)

密度函数为

(6)

失效率函数为

(7)

(4)最大似然参数估计

假设某个部件在某种失效模式下的寿命X(即可靠度)的分布函数是F(x，θ)，其中未知数θ∈Θ，Θ是任意非空集合。又设Y为非负广义随机变量(可取∞值)，表示右删失变量，与X独立。

由上文可知，动车组故障数据的产生类似于随机右截尾试验，即从分布函数为F(x，θ)的总体中，随机抽取n个个体，进行寿命试验(或观测)，对于每个个体(寿命是Xi，i=1，2，…，n)，相应的有个截尾时间Yi(i=1，2，…，n)，对第i个个体得到的观测值是XiΛYi。

基于以上，令ti=XiΛYi，δi=IXi≤Yi，得到的数据是(ti，δi)(i=1，2，…，n)，δi=1表示ti是寿终数据，δi=0表示ti是右删失数据。对于动车组故障数据，通过处理同样可以得到一组这样的数据， (t1，δ1)，…，(tn，δn)，这组数据的似然函数为

(8)

满足似然函数L(θ)最大的θ值即是我们需要求解的模型。

在上述似然函数中代入威布尔分布的表达式，威布尔分布为双参数分布族，所以得到如下的双参数的似然函数

(9)

其中，f(ti，η，β)和F(ti，η，β)分别为上述威布尔分布的密度和累积分布(考虑其可变参数η，β)[17-18]。

(5)使用梯度上升算法求取上述似然函数的极大值

首先需要设定合适的初始值。在初始情况下不对形状参数做过多的假设，令其初始值为β0=1，尺度参数以设计寿命代入η0，迭代过程为

(10)

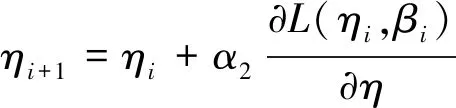
其中，α为足够小的迭代常数，此处设为α1=0.01，α2=1，并设置迭代过程改变量小于迭代常数时该过程终止，终止时的两参数值作为最终得到的分布参数[19]。

3.6 运用条件概率确定维修工作的时间间隔

(1)故障发生概率指标的确定

计划预防修间隔期按给定的故障发生概率来确定，以确保所需的安全性水平。经过对主流维修间隔确定模型的研究以及参考工程使用经验，给出了安全性、使用性和经济性的故障影响等级下一定故障发生概率的参考值，如表2所示。

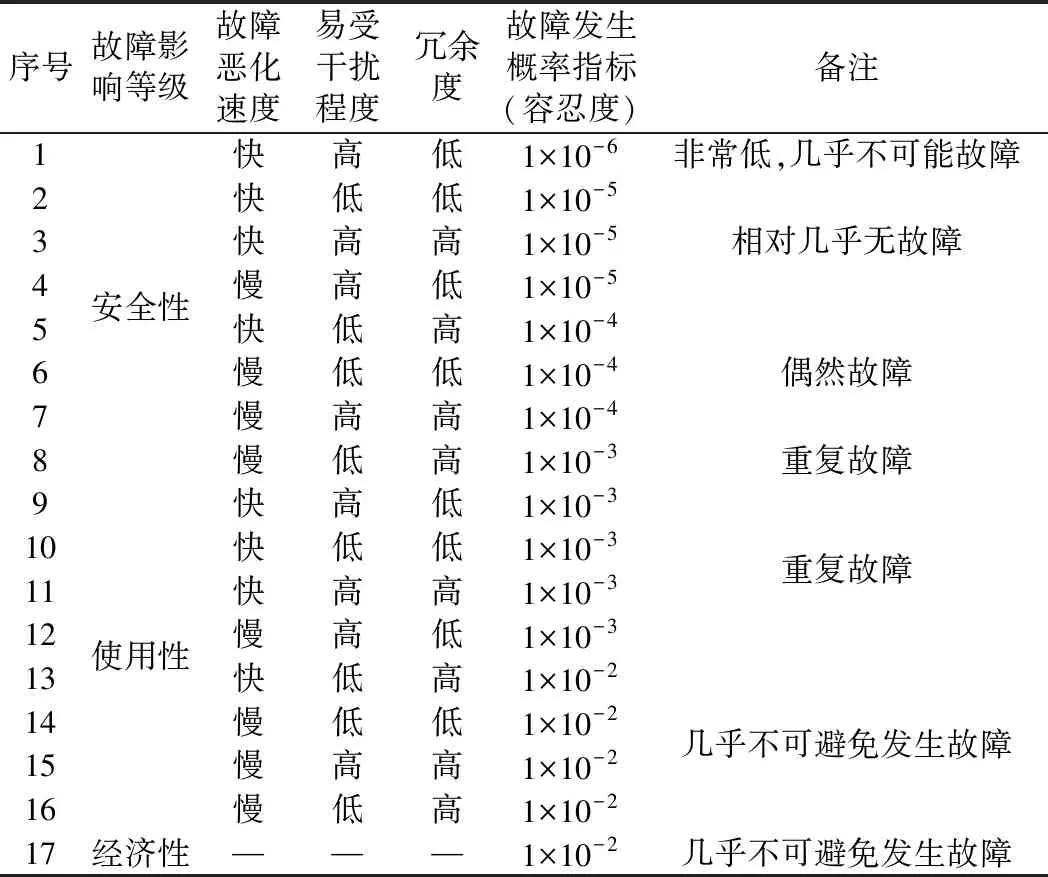
表2 故障发生概率参考值

(2)基于条件概率的时间间隔的确定

令X为故障发生时间点，间隔[Ti，Ti+1]内不发生的概率为

P(XTi+1|XTi)=1-p(12)

其中，p为两次维修间隔内允许的故障发生概率。

根据条件概率公式有

(13)

即

(14)

有

(15)

其中，R(x)为某种失效模式下部件的可靠度函数。

在已知两次维修间隔内允许的故障发生概率p后，即可确定维修的时间间隔[20]。

4 算例分析

为验证本文关于动车组运用维修间隔优化方法的合理性，现以CRH380B(L)型动车组空心车轴探伤为例进行分析。首先，整理了CRH380B(L)型动车组空心车轴超声波探伤故障数据，经过处理，得到空心车轴故障时走行公里数据，如表3所示。

通过R语言编程实现上述算法。根据本文参数估计计算得CRH380B(L)型动车组空心车轴寿命(可靠度)威布尔分布的形状参数β=0.760 2，尺度参数η=2 811 464 324。R Studio中拟合的图形如图8所示。

表3 CRH380B(L)型动车组空心车轴超声波探伤故障数据

图8 CRH380B(L)型动车组空心车轴超声波探伤数据威布尔案例分析

图8中红色实线表示拟合的寿命分布(可靠度)曲线，虚线表示置信区间边界曲线。

根据表2确定出动车组空心车轴材质缺陷故障的允许的故障发生概率，如表4所示。同时，根据式(15)计算得到CRH380B(L)型动车组空心车轴超声波探伤周期为：第一次探伤间隔为28万km；第二次探伤间隔为43万km；第三次探伤间隔为50万km…，逐步增大。

表4 动车组空心车轴材质缺陷故障的允许的故障发生概率

从现有统计的故障数据呈现出来的趋势可以看出(空心车轴故障数据统计截止2016年底)，动车组空心车轴的故障率越来越低，在一定的空心车轴可靠度的要求下，空心车轴探伤周期越来越长，呈现出了设备故障率浴盆曲线的早期故障期的规律，即主要由于制造和材质上的缺陷造成设备在使用初期，开始故障率较高，随着故障的排除，故障率逐渐下降。

同时，因供应商提供的10万km的探伤间隔是考虑了故障产生后，允许存在一次探伤未发现故障的情形，故28万km的理论计算探伤间隔也与实际10万km的探伤周期的工程要求较为接近。

5 结语

通过借鉴国内外航空、轨道交通领域主流的维修间隔确定方法理论，结合我国动车组运用实际，建立了一种适用于动车组运用维修使用的维修任务间隔确定方法。并利用CRH380B(L)型动车组已有数据，对所建立的理论模型进行了验证，验证结果与实际运用情形比较贴切。本文是对动车组现有维修周期优化方法的一次探索，通过理论计算结果，可以直观地判断出处于“维修不足”或“过度维修”状态下的维修项目，从而可以有针对性地去对维修间隔进行科学的调整。同时，本文所述方法是对现有方法的补充。