基于舒适度的悬挂式单轨平面曲线参数研究

郭士永，黄成名，胡江民，李三兵

(中铁工程设计咨询集团有限公司，北京 100055)

引言

目前，我国已有44个城市的城市轨道交通建设获得国家批复，主要为地铁、轻轨和跨座式单轨。对于大城市外围组团、中小城市及旅游景区，迫切需要中低运量、绿色环保、先进可靠、投资经济的轨道交通制式。悬挂式单轨属于中低运量系统，具有建设成本低、工期短、地形适应性强、运营安全、受恶劣天气影响小等优点[1]，近年来受到国内中小城市的关注。

悬挂式单轨与钢轮钢轨轨道交通存在较大差异，国内学者普遍将系统适应性[1-2]、车辆构造[3-5]、轨道梁[6-7]作为研究重点，对线路技术标准研究较少。平曲线参数是线路平面设计的控制性参数，与投资、养护维修、舒适度、轨道梁加工制造等密切相关。由于列车横向摆幅远大于传统轨道交通，且考虑列车横向倾斜不受轨道支撑的特性，故应将舒适度作为线路平曲线参数研究的主要因素。本文旨在研究不同舒适度要求、速度下线路平面最小曲线半径、缓和曲线长度。

1 悬挂式单轨车辆力学特性

悬挂式单轨车辆由转向架、车体、悬挂装置组成。顶部的转向架一般置于下部开口的箱型轨道梁内，车体悬挂在轨道梁下方。转向架两侧设导向轮，下部设走行轮，均采用橡胶轮胎。走行轮与内部走行面接触，实现走行功能；导向轮与箱梁内部的两侧表面接触，实现自导向功能，从而建立轮轨关系。

传统轨道交通设置轨道超高，使车辆曲线行驶受轨道支持力，平衡平面曲线行驶的离心力。悬挂式单轨离心力平衡机理与传统轨道交通不同，悬挂式单轨车辆采用柔性铰接悬挂，允许车体在一定角度范围内自主摆动。当车辆在曲线上行驶时，车体未被平衡横向加速度为aq，横向倾斜角、纵坡角分别为θ、γ，车体受力分析见图1。

图1 悬挂式车体受力原理示意

车体重力为mg，受到悬挂装置作用力为FN，车体曲线运动所需平衡的水平向、竖向离心力分别为Fh、Fv，可得

m(gcosγsinθ+aqcosθ)=Fvsinθ+Fhcosθ(1)

式中

Fh=m(Vcosγ/3.6)2/R(2)

Fv=m(V/3.6)2/Rv(3)

通过式(2)～式(3)分析，纵坡角越小横向离心力越大；竖曲线为凸曲线时，将增大横向离心力，考虑竖曲线半径较大，一般对横向离心力影响十分微弱。因此，不考虑竖曲线影响，当γ=0 rad时，横向离心力Fh最大，即

Fh=mgtanθmax+maq(4)

悬挂式单轨通过车体横向倾斜产生超高效应。假设车体横向倾斜角最大为θmax(rad)。当车体倾斜角θ≤θmax时，横向离心力Fh=mgtanθ且被平衡，此时产生平衡超高效应；当车体倾斜角θ=θmax且车体横向倾斜摆动未平衡的加速度为aq时，产生欠超高效应。因此，无论车体倾斜角大小，悬挂式单轨理论上不存在过超高效应。

2 舒适度与线路平曲线参数关系分析

2.1 线路平面舒适度评价指标

目前，列车乘坐舒适性评价尚未形成统一标准。国际标准ISO 2631以加速度大小来评判舒适度等级[8]。在国内铁路设计中，将最大超高及过欠超高允许值作为确定设计速度下曲线最小半径的决定因素，将超高顺坡率、时变率和欠超高时变率作为确定缓和曲线的基本因素[9-10]；地铁采用未被平衡横向加速度、最大超高及超高时变率为主要舒适度指标，并综合超高顺坡率等安全因素，用以计算不同速度下的最小曲线半径和缓和曲线长度[11-13]。

考虑悬挂式单轨特点，采用最大横向倾斜角与未被平衡横向加速度用于评价平面圆曲线舒适度，采用横向加速度时变率、未被平衡横向加速度时变率、横向倾斜角速度用于评价缓和曲线舒适度。

2.2 舒适度与线路平曲线参数关系

列车曲线行驶速度是影响舒适度的因素之一。线路平面曲线技术参数也与舒适度密切相关，主要包括圆曲线半径与长度、缓和曲线线形与长度、夹直线长度等。假设圆曲线半径R(m)，缓和曲线长度LS(m)，列车曲线匀速行驶的速度V(km/h)，圆曲线行驶的横向倾斜角θ。以下构建各舒适度指标与线路平曲线参数间定量关系。

2.2.1 倾斜角与平曲线半径关系

悬挂式列车匀速通过曲线时，圆曲线上的车体倾斜角、加速度均是曲线段内的最大值。最大横向加速度完全由车体倾斜提供时，车体倾斜角为平衡倾斜角，用θe(rad)表示。根据动力学原理，可得平衡倾斜角与速度、半径间关系，如式(5)所示

(5)

考虑车辆最大倾斜角θmax的限制，故车体的最大倾斜角θ为θe和θmax的较小值，即

(6)

2.2.2 未被平衡横向加速度与平曲线半径关系

当平衡倾斜角θe≤θmax时，车辆通过圆曲线段时不产生未被平衡横向加速度。当平衡倾斜角θeθmax时，车辆圆曲线段的横向倾斜角维持θmax不变，产生未被平衡横向加速度aq=gtanθe-gtanθmax，结合式(4)和式(5)推导可得

(7)

2.2.3 横向加速度时变率与缓和曲线长度关系

横向加速度时变率β是列车匀速通过缓和曲线的横向加速度增量Δa与行驶时间t的比值，即β=Δa/t。其中，当曲线间存在夹直线时，列车通过缓和曲线的加速度增量及时间分别如下

Δa=V2/(3.62R)(8)

t=3.6LS/V(9)

则横向离心加速度时变率为

(10)

2.2.4 横向倾斜角速度与缓和曲线长度关系

假定车体匀速通过曲线，则车体横向倾斜角速度ω为缓和曲线段车体倾斜角变量Δθ与所需时间t1的比值，即

ω=Δθ/t1(11)

当θe≤θmax时，横向倾斜角速度由式(5)和式(11)推导可得

(12)

当θeθmax时，列车在缓和曲线上行驶，随着曲率k增大，列车倾斜角逐渐增大。当k=k0，倾斜角θ=θmax，该点至曲率为零段缓和曲线长度定义为l1(m)。此后曲率继续增大，而倾斜角受悬挂装置构造限制不能继续增大，该段产生未被平衡横向加速度，车体倾斜角维持θmax不变。故曲率k0和车体横向倾斜角速度ω分别为

(13)

2.2.5 未被平衡横向加速度时变率与缓和曲线长度关系

当列车在曲率k≥k0的缓和曲线段行驶时，产生未被平衡的横向加速度。定义该段缓和曲线长度为l2，且l2=ls-l1。未被平衡横向加速度时变率均值λ为该段缓和曲线未被平衡横向加速度变化量与匀速通过时间的比值，依式(7)推导可得

(15)

3 基于舒适度的悬挂式单轨平面曲线参数计算

3.1 舒适度要求

最大横向倾斜角应保证乘客站立稳定。国内，无砟轨道高速铁路、跨座式单轨最大设计超高分别为175 mm、12%[14-16]，对应车体倾斜角依次为6.654°，6.843°，中低速磁浮最大超高横坡为6°[17]。地铁设计超高最大值为120 mm，即倾斜角为4.574°。多年运营经验表明，各类轨道交通最大车体倾斜均无乘坐不良反应。考虑悬挂运行横向摆动大的特点及站席舒适性，本文中最大横向倾斜角为6°。

未被平衡横向加速度各国取值不同。根据实验，该指标为0.4 m/s2时，乘客稍有感觉，列车运行平稳；0.5～0.65 m/s2为乘客“有些不舒服感觉但可以忍受”的范围；0.8 m/s2及以上时，乘客明显感觉不舒适[8-9]。国内铁路将未被平衡的横向加速度分为优秀、良好、一般三个等级[9-10]，对应的分界值为0.27，0.40，0.60；地铁未被平衡的横向加速度最大值0.4 m/s2[11-12]。本文将0.25，0.40，0.50，0.60 m/s2作为舒适度优秀、良好、一般、困难对应的未被平衡横向加速度最大值。

横向加速度时变率是衡量缓和曲线舒适度的主要指标。重庆跨座式单轨横向加速度时变率最大值为0.3 m/s3[14]，铁路、地铁中允许的超高时变率分别为38[10]，40 mm/s，换算为加速度为0.25，0.26 m/s3。本文选取横向加速度时变率最大值一般采用0.25 m/s3，困难时为0.30 m/s3。

文献[18]研究表明，当超高时变率达到55 mm/s时，垂向舒适度达到限值。换算成横向倾斜角速度分别为0.030 0，0.036 7 rad/s。地铁采用的超高时变率最大值为40 mm/s[12]，折算成角速度为0.026 7 rad/s。参考文献[19-20]，本文建议横向角速度最大值一般条件下为0.026 7 rad/s，困难条件下为0.036 7 rad/s。考虑舒适度要求，未被平衡横向加速度时变率最大值一般情况下为0.15 m/s3，困难情况下为0.30 m/s3。

平曲线舒适度指标要求见表1。

3.2 最小平面曲线半径研究

悬挂式单轨最小平面曲线半径不小于车辆构造半径，并且根据速度与横向倾斜角、未被平衡加速度等舒适度要求确定。车辆构造半径为车辆构造、性能所允许通过曲线的最小半径，取值30 m。由式(7)可得特定速度下平面最小曲线半径

表1 平曲线舒适度指标要求

(16)

式中，θmax取6°，折合为0.104 7 rad；[aq]根据不同舒适度要求取值，m/s2。由式(16)可知，速度不变情况下，横向倾斜角、未被平衡横向加速度取值越大，半径越小。将计算参数代入上式，得出满足不同舒适性要求和速度的最小圆曲线半径。最小半径建议值取5的倍数。最小曲线半径见表2。速度80 km/h条件下，舒适度优秀、一般、困难的最小曲线半径分别为386，323，303 m，建议值取为325 m。在城市密集建筑环境中，应适当降低舒适度要求，采用较小的半径以适应复杂的城市环境。

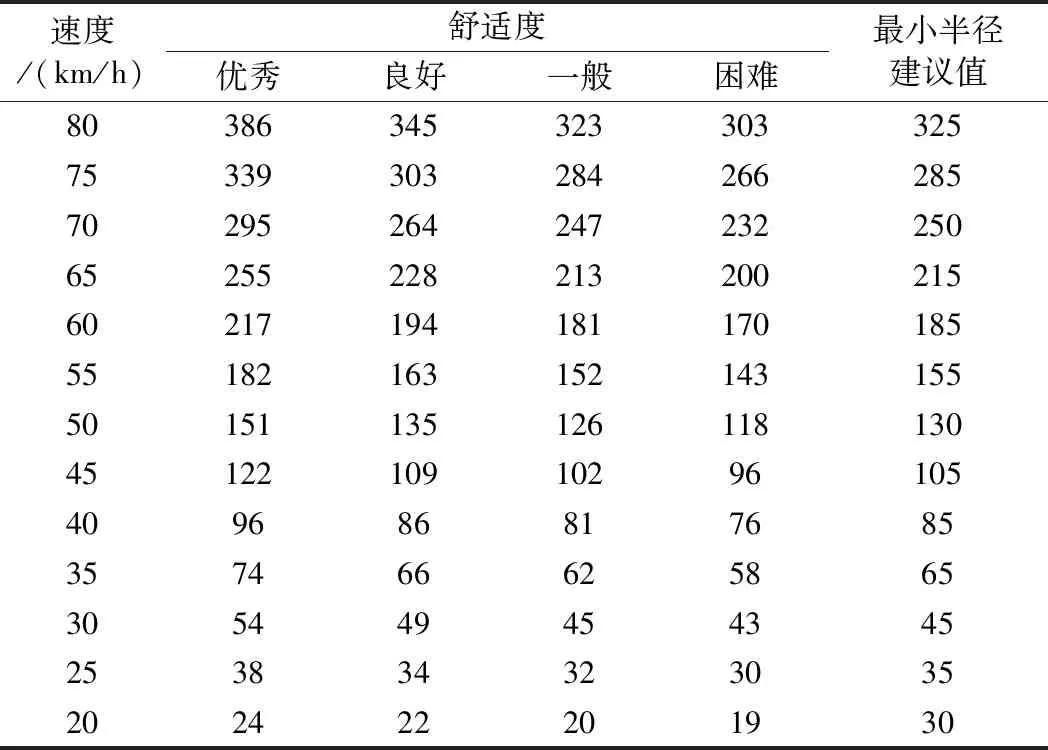
表2 不同舒适度下的最小曲线半径 m

3.3 缓和曲线长度研究

缓和曲线能够实现车体倾斜、横向加速度、未被平衡加速度渐变过渡。缓和曲线最小长度不应小于一节车辆的全轴距LYZ，根据车辆厂商提供的数据，一般取10 m。悬挂式单轨缓和曲线最小长度应综合横向加速度时变率、倾斜角速度、未被平衡横向加速度时变率等舒适度要求及全轴距，并取其中的最大值。

据横向加速度时变率最大值[β](m/s3)及式(10)可得缓和曲线长度

(17)

(1)当θe≤θmax时，缓和曲线全段不产生未被平衡横向加速度，l2=0，由式(12)、倾斜角速度最大值[ω]反推的最小值l1

(18)

则缓和曲线最小长度为

LS，min=max(L1，l1，LYZ)(19)

(2)当θeθmax时，缓和曲线曲率较小段(k≤k0)车体倾角逐渐达到最大，缓和曲线曲率较小段(kk0)产生未被平衡横向加速度，则将倾斜角速度最大值[ω]、未被平衡横向加速度时变率最大值[λ]分别代入式(14)、式(15)，反推l1、l2为

(20)

则缓和曲线最小长度

LS，min=max(L1，l1+l2，LYZ)(21)

缓和曲线最小长度按照式(17)～式(21)计算，取5的整倍数。经计算，当半径R≥479 m时，可满足速度80 km/h、倾斜角不大于6°且无横向未平衡加速度。故本文重点研究匹配半径不超过500 m的缓和曲线长度，计算结果见表3。半径较小时，缓和曲线最小长度取决于倾斜角速度、未被平衡横向加速度时变率。例如，时速80 km/h、R=300 m，L1两级取值分别为150，120 m，l1+l2两级取值分别为180，110 m，故舒适度均较好情况下缓长为180 m。

表3 不同舒适度下的缓和曲线长度 m

注：[ω,λ]1表示[ω]=0.026 7，[λ]=0.15；[ω,λ]2表示[ω]=0.036 7,[λ]=0.30；[β]1表示[β]=0.25；[β]2表示[β]=0.30。

4 结论

舒适度是影响悬挂式单轨线路平面设计的基本因素。运用动力学理论分析了悬挂式车辆力学特性，选取平曲线舒适度指标并构建其与平面参数的关系模型，基于舒适度要求确定线路平面最小曲线半径、匹配缓和曲线长度。研究原理、成果可用于悬挂式单轨线路优化设计及技术标准制定。主要结论如下。

(1)悬挂式单轨列车曲线行驶时，其倾斜角不受轨道限制随速度增大而增大。乘客的横向摆幅远大于传统轨道交通。在悬挂式单轨线路设计中，应重视线路平面设计对舒适度的影响。

(2)悬挂式单轨车辆最大倾斜角由构造允许倾斜角及轨道梁走行面倾角综合确定，不同厂家的构造允许倾斜角不同。各舒适度指标可分级取值。本文以最大倾斜角6°为例，基于不同舒适度要求确定平面曲线半径及匹配的缓和曲线长度。在工程设计中，可按照关系模型，根据厂家提供的车辆倾斜角，结合线路功能特点、行车需求、投资、运营维护等因素，合理确定线路平曲线参数。