某电厂发电设备可靠性建模及状态预测

牛腾赟

(中国大唐集团科学技术研究院有限公司华中电力试验研究院，郑州 450000)

0 引言

设备可靠性是指设备在指定的条件和时间内，实现特定功能的能力。在生产过程中通常将设备分为2种，一种为可修复设备，另一种为不可修复设备[1]。前者在设备出现故障并失效后，能通过人员维修使其正常运转，实现原有的功能；后者出现故障并失效后，不能通过维修使其正常运转，只能更换新的设备来代替原有设备以保持系统的正常运转[2]。通常把不可修复设备的可靠性，称为狭义可靠性，可靠性只表示设备在某一时间区间内出现设备失效可能性的大小；但是对于可修复设备来说，设备的可靠性不仅体现当前设备能实现特定功能的能力，而且还体现了设备可修复性[3]。可修复性是表示设备发生故障失效后，能否通过快速修复使设备恢复至正常运转状况的特性。所以，对于可修复设备来说，可靠性的定义更加广泛，形成了广义可靠性的概念，称之为设备的可用性，可用性表示设备在其寿命周期中被使用的程度[4]。火电厂大部分设备都是可修复设备，本文构造的数学模型所应用的对象选定为可修复设备。在现场实际生产过程中，检修员通过日常检修维护，对发电设备发生故障的频率进行统计计算，能全面发现故障规律性。通过建立并完善设备档案，录入设备使用、故障、维修等数据，及时了解设备的历史运行参数，并使用数理统计的方法对设备可靠性进行分析和判断[5-6]。

但是当前电厂存在对点检数据浪费的情况，不能有效地对点检数据进行处理分析，造成点检工作效率不高。

本文结合我国电厂巡点检数据分析预测现状和某热电厂的实际情况，以发电设备状态参数为研究对象，建立了基于灰色理论的数学模型，对点检数据进行处理，进行了状态参数的预测和评价；使用“改进灰色模型”通过引入m点均算因子，对具有波动性的原始发电设备运行参数序列进行m点均值处理，使原始数据满足灰色模型光滑性的要求。结果表明，使用改进的灰色模型能更加准确地预测和评价该电厂发电设备的运行状态，最终实现了对点检数据处理预测的目的。

1 灰色理论及灰色预测建模

1.1 灰色系统理论

灰色系统理论的具体内容可以表述为一套完整的基于灰色朦胧集的理论体系，其将灰色模型作为最核心的模型体系，能够有效地完成系统分析、评价、建模、控制以及优化等过程。

在灰色理论中，最核心的是灰色模型。灰色模型能够对信息量较少时的建模过程进行分析，并不断对模型进行改进与优化，这能够使灰色模型(GM)具有较高的优越性，尤其是在无法确定系统的概率特征时也能够达到最佳的效果[7-8]。

1.2 GM(1,1)预测模型及建立

灰色模型即为对灰色数列构建的模型。传统建模方式一般基于数据序列来构建差分方程，而灰色模型并不是采用这种方式，其主要是使用原始数据序列作数据来构建微分方程。当前使用最多的灰色预测模型是GM(1,1)模型[9]。此模型使用了随机的原始时间序列，然后采用了一个一阶微分方程对累加之后的时间序列进行逼近。

建立灰色预测模型的首要工作是要生成数据，此过程需要向模型提供一些中间信息，同时需要降低原始序列的随机性，一般可以采用累加法或者是累减法[10]。下面对两种生成方法进行具体介绍。

1.2.1 累加生成

首先是累加生成方法，这种方法已经得到了较为广泛的应用。如果采用累加生成法来得到最新的时间序列，能够对其随机性进行适当的弱化。

如果原始序列时

x(0)={x(0)(k)|k=1，2,…，n}=

(x(0)(1)，x(0)(2)，…，x(0)(n)} ，

(1)

则其生成序列为

x(1)={x(1)(k)|k=1，2,…，n}=

(x(1)(1)，x(1)(2)，…，x(1)(n)} ，

(2)

两者能够满足如下关系：

(3)

r次(一般)累加生成下述关系

(4)

(5)

易知，r-1次到r次的累加为

x(r-1)(k-1)+x(r-1)(k) ，

(6)

(7)

采用累加生成方法能够得到不同类型的非负序列，或者是将其转化成递增序列。如果随机的原始数据进行累加生成之后可以形成比较强的规律特征，甚至可以近似地通过函数进行表征，此函数即为生成函数，此时得到的生成模型也可以称为“累加生成模型”。

1.2.2 累减生成

累减生成方法即为对原始数列相邻两个数据进行相减之后获得的序列，也可以将其理解为是与累加生成相反的运算。因此，通过累减生成能够直接将累加生成序列进行还原得到原始数列。

如果x(r)表示r次生成序列，x(r)作i次累减生成，即为α(i)，其表达式为

(8)

灰色预测模型GM(1,1)是一个一阶微分方程模型，能够实现数列预测功能，在构建灰色预测模型GM(1,1)时，需要按照合理的过程进行，具体过程如下。

建立GM(1,1)需要使用数列

x(0)={x(0)(1)，x(0)(2)，…，x(0)(n)} ，

(9)

对其进行1-AGO之后即可得到

(10)

建立x(1)的白化方程

(11)

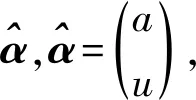
(12)

yN=(x(0)(2)，x(0)(3)，…，x(0)(n))T。

此方程的解可以表示为

(13)

对其进行1-IAGO之后可得到预测模型

(14)

1.3 模型精度校验

为了提高对点检数据的预测精度，需要利用更多可靠的信息对这种不确定性进行检验，然后得到准确性更高的数据。本文采用表格法对GM(1,1)预测模型的预测精度进行检测，精度校验等级参照表见表1。

表1 精度校验等级参照Tab.1 Reference table for accuracy class

此方法需要基于GM(1,1)模型的具体位置来确定预测模型精度，预测精度等级越低，表明预测效果越好。

设原始序列

X(0)={x(0)(1)，x(0)(2)，…，x(0)(n)} ，

(15)

预测序列为

(16)

1.3.1 平均相对误差

令残差ε(k)以及相对误差Δ(k)分别为

(17)

(18)

(19)

1.3.2 方差比值

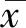
(20)

(21)

(22)

(23)

方差比值

(24)

2 灰预测模型的改进

由于发电设备随着运行时间的增加，运行时状态数据也在不断刷新，如果将其考虑在数学模型内，预测数据量也会持续增加，此时基于全部数据构建的GM(1,1)灰色模型即为全息模型。在实际情况中，由于新的状态参数的刷新和补充，新数据为数学模型带来了扰动和驱动元素，建立的预测灰色模型会由于新数据的加入而出现全新的变化，随着发电设备的不断运行，产生的新数据逐步增加，先前的数据逐渐会失去意义，甚至会对新数据的处理带来影响，因此需要将旧数据进行处理。

此外，由于发电设备运行时间增加，越来越多的新数据进入数据库，会使新的数据列的维数持续增加，运算工作量愈发繁重，对硬件的配置提出了更大的挑战。故改进的灰色GM(1,1)模型需要对数据处理过程进行简化，其采用的方式如下：首先需要保证原始数据维数不断，当出现新的运行数据时，需要将先前的运行信息去除，从而保证数据的质量与时效性，使预测精度得到较大的提升。GM(1,1)等维新息模型即为

Y(0)={y(0)(n-k)，y(0)(n-k+1)，…，

y(0)(n)}n≥4，n>k，

(25)

式中：Y(0)为原始数据序列，模型的维数为

n-(n-k)=k。

由于使用范围的限制，传统的GM(1,1)模型对波动数据的处理结果不能满足发电厂对预测数据的要求。出现这种情况的原因是波动数据无法满足GM(1,1)模型的光滑性条件，因此通过某种手段将没有规律的波动数列处理为与指数变化规律相仿的序列，成为解决原始数据不能满足灰色模型光滑性要求的关键所在。本节所使用的“改进GM(1,1)模型”，引入了均算因子，对具有波动性的原始发电设备的运行参数序列Y(0)={y(0)(1)，y(0)(2)，…，y(0)(n)}进行m点均值处理，处理后使Y(0)序列转化为新序列X(0)={x(0)(1)，x(0)(2)，…，x(0)(n)}，即

(26)

因为最终预测结果会受到原点和原点附近值的干扰，且干扰很强，故通常取m=3，此方式可以保证原始序列不会出现特征变化，也可以将随机序列的变化规律整理为类指数变化规律。如果原始序列数值变化幅度大，那么m的值要偏大，以达到均值处理完毕时，序列为类指数变化的目的。

对X(0)做一次累加生成序列X(1)={x(1)(1)，x(1)(2)，…，x(1)(n)}，其中

(27)

设Z(1)={z(1)(1)，z(1)(2)，…，z(1)(n)}为X(1)的紧邻均值生成序列

z(1)(i)=0.5x(1)(i)+0.5x(1)(i-1)

i=2，3,…，n，

(28)

然后构建GM(1,1)模型的灰色微分方程

x(0)(k)+az(1)(k)=b。

(29)

白化微分方程可以表示为

(30)

采用最小二乘法计算灰系数向量

(31)

其中

(32)

k=1，2，…，n。

(33)

采用一次累减操作得到预测序列

k=1,2,…,n。

(34)

3 改进灰预测模型的应用

为了对点检数据进行处理，本文选择了某电厂给水泵的点检数据。通常情况下，给水泵出口给水压力要比锅炉内水冷壁中工质的压力高25%以上，这样工质就能克服高压加热器、省煤器和高压给水管道的阻力进入汽轮机或进入汽包。整个火力发电机组的正常运行与给水泵的状态有着密不可分的关系，对给水泵的各项状态参数实行检测、记录和预测成为了火电厂安全生产中的重要一环。

该电厂给水泵布置采用国内主流的方案，即“额定容量的汽动给水泵(运行泵)+ 额定容量的电动调速给水泵(启动/备用泵)”方案。给水泵采用6×14CSB-4型锅炉给水泵，其工作水温为210 ℃，入口压力为1.06 MPa，出口扬程为2 143 m，额定流量为750 m3/h，额定转速为5 680 r/min。本文选取了此电厂A汽动给水泵实际运行参数，记为数列P={p1，p2，p3，p4，p5，p6}，单位分别对应为μm，MPa，℃，℃，℃，MPa，其中pi表示的是给水泵振幅、给水泵出口压力、给水泵轴承金属温度、冷油器出口油温、密封冷却水温度以及给水泵润滑油压，以这6个参数的状态作为给水泵运行状态的评价指标。例如：冷油器出口油温超标，会使润滑油黏度降低，降低轴承的承载能力，油膜不稳定，加剧油质劣化；油温低于标准温度时，润滑油的黏度就会变大，当轴承与轴颈之间的最小间隙比润滑油形成的最小油膜厚度大的时候，就会导致油膜被破坏，并进一步造成轴颈轴瓦发生摩擦引起烧瓦。密封冷却水温度超标，会造成密封损坏。给水泵润滑油压偏低，可能是润滑油系统有外漏现象，润滑油系统管道存在法兰密封不严、法兰螺栓松动、管道焊缝泄漏等风险[11]。通过对以上参数进行记录分析，可以了解给水泵的运行状态，为给水泵的故障诊断提供参考。

该电厂每隔一天对#1机组汽动给水泵A泵进行数据采集，给水泵出冷油器口油温数据见表2。由表中数据可知，冷油器出口油温为升高态势，但不明显，有明显波动。从第7次采集数据之后，冷油器出口油温高于阈值46 ℃，而后依然有上升的态势，这预示着A汽动给水泵的冷却系统可能存在故障，影响电厂正常运行。为了提前发现故障征兆，本小节使用3种模型对A汽动给水泵的冷油器出口油温度进行预测。

表2 给水泵冷油器出口油温Tab.2 Oil temperature at feed water pump oil cooler outlet ℃

表3 数学模型预测给水泵冷油器出口油温数据Tab.3 Oil temperature at feed water pump oil cooler outlet predicted by mathematical model

本节采用“改进灰色GM(1,1)模型”和经典GM(1,1)模型，建立了5维新息的灰色GM(1,1)模型，其含义就是用5个不间断的给水泵冷油器出口油温的实测值，来预测第6天的冷油器出口油温；为了验证和对比“改进灰色GM(1,1)模型”的预测精度，本节使用Matlab软件，采用四阶曲线拟合模型，用解析表达式逼近离散数据，使离散数据公式化。在电厂数据处理的实践中，离散点组或数据往往是各种物理问题和统计问题有关量的多次观测值或试验值，它们是零散的，不仅不便于处理，而且通常不能确切和充分地体现出其固有的规律，这种缺陷可由适当的四阶曲线解析表达式来弥补，使用此模型对#1机组A给水泵冷油器出口油温数值进行拟合预测，其预测结果见表2，曲线拟合模型与实测值对比如图1所示。

图1 曲线拟合模型与实测值对比Fig.1 Comparison between curve fitting model and measured value

3种模型预测结果见表3，本文采用表格法进行精度检验。由表3可知，改进灰色GM(1,1)模型平均相对误差为2.427%，方差比值0.075，由表1可知改进GM(1,1)模型的平均相对误差达到了二级精度，方差比值达到了一级精度；经典GM(1,1)模型的平均相对误差为4.279%，达到了二级精度，方差比值为0.498，达到了二级精度；四阶曲线拟合模型的平均相对误差为8.600%，为三级精度，方差比值为3.107，预测精度远低于四级精度标准。可以发现“改进灰色GM(1,1)模型”的预测精度最高，其预测效果也最好，适合在火电厂发电设备的状态预测中进行实践应用。

3条预测曲线的变化趋势如图2所示，改进灰色GM(1,1)模型的预测趋势曲线最逼近实际现场测得的冷油器出口油温数据，其结果比较真实地反映出了生产运行时状态参数的波动过程；而传统灰色GM(1,1)模型与四阶曲线拟合模型的出口油温预测数值不能很好地反映实际的冷油器出口油温波动趋势，尤其是四阶曲线拟合模型的预测结果与实际出口油温的变化态势相差略大，不能应用于电厂实际生产过程中。

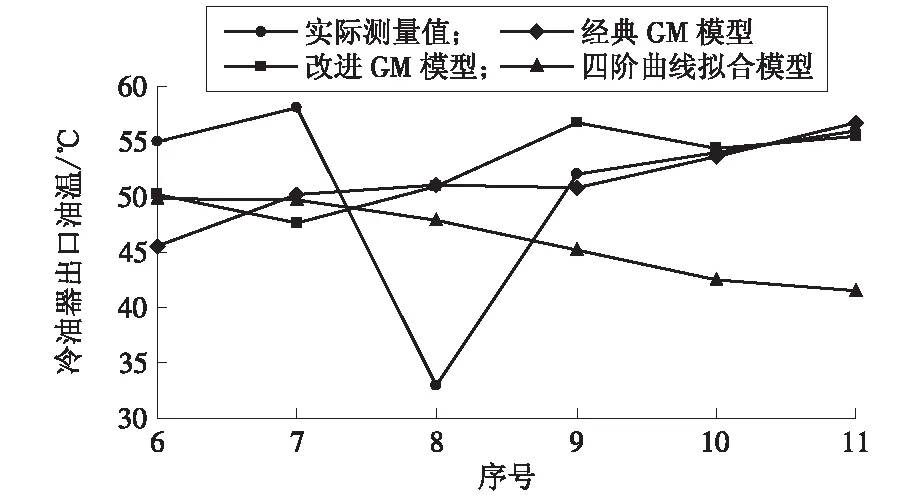
图2 3种预测模型预测值对比Fig.2 Comparison of predicted values of three prediction models

4 结论

比较可得：对于实际生产现场的具有波动性的设备状态参数的预测，使用“改进灰色GM(1,1)模型”可以得到预期的结果，其预测值拥有很高的精度，所以在火电厂发电设备状态参数的预测中，针对易受环境影响且波动性较强的设备，采用“改进灰色GM(1,1)模型”进行预测能得到较好的结果，适合用于处理电厂中大量的点检数据。