图像分类卷积神经网络的反馈损失计算方法改进

周 非，李 阳，范馨月

(重庆邮电大学 通信与信息工程学院，重庆 400065)(重庆邮电大学 光通信与网络重点实验室，重庆 400065)

1 引 言

诞生于上世纪80年代末的卷积神经网络(Convolutional Neural Networks，CNN)目前广泛应用于计算机视觉领域[1]，在最近十几年里不断刷新着图像分类精度的极限，并同时在目标检测[2，3]，目标跟踪[4，5]，图像分割[6]，以及人脸识别等领域取得丰硕的研究成果[7].在应用于图像分类的过程中，卷积神经网络经历了从1998年Lecun Y等人提出的LeNet[8]，到2012年Krizhevsky等人提出的AlexNet[9]，再到2015年Szegedy等人提出的GoogLeNet和2016年Kaiming等人提出的ResNet[10，11]，以及后来的改进版本[12，13].这期间出现了ReLu等新型激活函数[14，15]，Inception和残差结构等卷积神经网络结构[10，11]，与Batch Normalization等优化算法[12].整体而言，卷积神经网络在朝着“更深”和“更宽”的方向发展.

“更深”指通过增加CNN的层数，来提高卷积神经网络分类性能.泛逼近定理指出，当给定足够的容量，一个单层的前馈网络就足以表示任何函数，但是，这个层可能会非常大，并且网络容易出现过拟合等问题，所以实际上构建一个单层CNN并不可行，学术界对此的主要解决办法就是增加CNN的深度.2012年论文[9]提出的AlexNet卷积神经网络仅有8个参数层，而2015年发表的论文[10]提出的GoogLeNet就已经增加到22层.但是研究人员发现在逐渐增加网络深度的同时，梯度消失问题越来越严重，导致CNN随着层数的增加，性能反而有所下降.而ResNet卷积神经网络所采用的一种残差网络结构，在一定程度上缓解了这一难题，使得卷积神经网络层数的进一步加深成为可能，论文[11]已经实现了一个超过1000层的图像分类卷积神经网络.

但“更深”并不是提高图像分类卷积神经网络性能的唯一途径，研究发现“更宽”也能提高CNN的性能.论文[16]指出，对于ResNet所提出的残差网络结构，随着模型的加深，并不能保证梯度在反馈训练过程中能够流经每一个残差模块，甚至在整个训练过程中，可能只有很少的几个残差模块能够学习到有用的特征表达，大部分残差模块对图像分类能力的提升影响并不大.为此该论文提出了一种网络层数较少，但每层的通道数更多的CNN结构.即所谓的“更宽”，通过扩展卷积层的通道数，优化参数利用效率，从而提升卷积神经网络对图片的分类能力.

受“更宽”思路的启发，本文提出通过提高卷积神经网络输出向量的维度，同时增加不同类别训练样本标签间的汉明距离，从而提高卷积神经网络对图像的分类能力.即在卷积神经网络的训练过程中，使用维度更高、不同类别间最小汉明距离更大的标签进行训练，以此增大网络对不同类别图片的输出距离.更大的输出距离能够提高卷积神经网络判决时的容错能力，提升网络对图片的分类性能.

2 传统图像分类卷积神经网络的缺陷

当前用于图像分类的卷积神经网络主要通过独热编码处理训练样本的标签，然后结合softmax激活函数和对数似然损失函数计算训练过程中CNN的实际输出与理论输出之间的误差，并通过随机梯度下降算法(Stochastic Gradient Descent，SGD)更新权重和偏置.其权重和偏置的更新过程遵循的原则如公式(1)和公式(2)所示，公式中C为反馈误差，η为更新步长.

(1)

(2)

本节主要分析这种传统图像分类卷积神经网络存在的缺陷以及改进的思路.

2.1 对数似然损失函数

对数似然损失函数常被用来衡量训练样本图片通过CNN后的实际输出与理论输出之间的误差，其定义如公式(3)所示.

C=-∑kyklogak

(3)

其中y表示CNN的理论输出，a表示实际输出，C表示实际输出与理论输出之间的误差.由于权重w与本层输入x间存在关系z=wx+b，定义激活函数的表达式为a=σ(z)，则可得到对数似然损失函数关于权重w和偏置b的导数如下.

(4)

(5)

2.2 softmax激活函数

softmax激活函数为图像分类卷积神经网络引入非线性化操作，其数学表达式如公式(6)所示.

(6)

当i=j时，可得到该激活函数的导数为

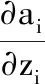
(7)

当i≠j时，可得到该激活函数的导数为

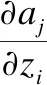
(8)

将softmax激活函数的导数带入公式(4)和(5)中，可将对数似然损失函数关于权重和偏移的导数公式化简如下.

(9)

(10)

2.3 独热编码

用于训练图像分类卷积神经网络的样本标签通常使用独热编码进行预处理.经过处理后的每个样本标签只有一个数位上的值为1，其余数位上的值均为0.因此公式(9)和公式(10)中∑kyk=1，即可将这两个公式进一步化简如下.

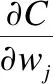
(11)

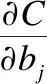
(12)

当图像分类卷积神经网络使用对数似然损失函数、softmax激活函数和独热编码计算训练过程中的反馈损失时，其权重更新公式(公式(1))和偏置更新公式(公式(2))的最终结果如公式和公式所示.

(wj)new=(wj)old-ηxj(aj-yj)

(13)

(bj)new=(bj)old-η(aj-yj)

(14)

公式(13)和(14)公式表明，当训练过程中实际输出与理论输出的误差较大时，权重和偏置的更新速度较快，当误差较小时，更新速度较慢，这样的特性有利于提高网络训练时的收敛速度.

2.4 问题描述

以上推导的就是传统图像分类卷积神经网络在训练过程中普遍使用的反馈损失计算方法.测试时，只需要找出输出向量的最大值所处位置，即可判断出测试样本所属类别.这种判决方式存在的问题是，由于卷积神经网络最终的分类结果仅依靠输出向量的最大值进行判定，当输出向量的某一位置受到较大的干扰时，容易造成最终结果的误判.为此本文提出充分利用卷积神经网络输出向量在各个维度上的信息.训练时，通过增大不同类别间标签的维度和最小码间距离，从而提高卷积神经网络对不同类别样本的区分能力.测试时，根据先前标签的制定规则，计算出卷积神经网络的输出与标签集合中对应的最小欧几里德距离，该最小距离所对应的标签即为最优的判决结果.

3 改进图像分类卷积神经网络

本文提出通过增加不同类别的图片经过CNN后输出向量间的最小距离，从而提高卷积神经网络判决时的容错能力.对此，本文的具体解决方案是增加CNN输出向量的维度并使用信道编码中的分组码处理训练样本的标签，同时选择合适的激活函数和损失函数计算反馈损失.

3.1 引入分组码处理样本标签

分组码是通信中广泛使用的一种信道编码方式，其通过增加编码冗余来提高信道的容错能力，并且其能够纠正的错误位数t与码组的最小汉明距离d之间存在的关系如公式(15)所示.

d≥2t+1

(15)

当分组码能够纠正的错误位数越多，其最小码距就越大.使用最小码距越大的分组码来做训练样本的标签时，不同类别的图片经过CNN后输出向量的区分度就越大.因此，设计CNN训练样本标签的问题就转化成求解分组码的监督矩阵问题.

对于(n，k)线性分组码，其监督矩阵的典型矩阵如公式所示，其中I为(n-k)阶单位矩阵.

H=(I|P)

(16)

并且对于线性分组码，最小码距为d的充要条件是监督矩阵H中任意d-1列线性无关.因为I是单位矩阵，为了使得d尽可能大，P的每一列所含1的个数需要尽可能多，同时需要保证矩阵P线性无关的列数尽可能大.

例如对于一个10分类的图片数据集，使用4比特的信息位就能够表示其全部类别，如果设定卷积神经网络的输出向量维度为10，那么训练样本标签的编码问题就转化为求解一个(10，4)分组码问题.通过设计监督矩阵，然后转换为对应的生成矩阵，就能够生成一组最小码距较大的训练样本标签集.本文在设计监督矩阵的时候，采用了一种类似列举编码的方法[17].对于(10，4)线性分组码，其监督矩阵的行数为6，列数为10，并且其前6列构成一个单位矩阵.本文构造的监督矩阵如下所示.

设生成矩阵为G=(I|Q)，并且由于监督矩阵和生成矩阵存在的关系如公式所示.

H·GT=0T

(17)

可以将生成矩阵转换为公式所示.

G=(I|PT)

(18)

对于上文所描述的(10，4)线性分组码，可以得到其生成矩阵如下.

因此，根据c=u·G，可以得到卷积神经网络10分类训练样本的一组标签如下所示(每行为一个标签类别).

通过观察许用码组C可以看出，该组标签的最小码距为4.并且通过观察监督矩阵H，可以发现监督矩阵H的任意4列线性无关，这也符合前面所提到的最小码距为d的充要条件是监督矩阵H中任意d-1列线性无关这一约束条件.下文的仿真还会使用一种(20，4)的线性分组码，其构造步骤与上述方法一致.

3.2 改进反馈误差的计算方式

本文分别使用softmax和sigmoid两种激活函数来计算卷积神经网络训练时的反馈误差，并对比分析这两种激活函数在图像分类应用中的优劣.

为保证权值与偏置的更新快慢与反馈误差的大小保持一致，当使用softmax激活函数作为CNN最后一层的激活函数时，本文使用对数似然损失函数计算反馈误差.但不同于独热编码，当使用分组码处理样本标签时，存在

即每个样本标签的码重不再为1，所以反馈损失关于权重和偏置的导数变为如下所示.

(19)

(20)

尽管公式(19)和公式(20)中输出向量a前面有标签的码重作为系数，但并未改变权重和偏置的更新快慢和反馈误差大小保持一致这一特性，这样的特性能够让CNN取得较快的收敛速度，基于这个原因，本文选择了这一组合作为卷积神经网络反馈误差的计算方式之一.

sigmoid激活函数的定义和导数如公式(21)和公式(22)所示.

(21)

(22)

当选择sigmoid作为卷积神经网络最后一层的激活函数时，本文使用交叉熵作为对应的损失函数.下面分析这样选择的合理性.

交叉熵的数学表达式如公式(23)所示，其中y为训练样本的标签，a为网络的实际输出.

(23)

由于a=σ(z)，z=wx+b，可以推导出交叉熵对权重w和偏置b的导数如下.

结合sigmoid激活函数的导数，可以得到交叉熵损失关于权重和偏置的导数，如公式(24)和公式(25)所示.

(24)

(25)

然后可以得到对应的权重和偏置的更新表达式如公式(26)和公式(27)所示.

(26)

(27)

从公式(26)和公式(27)可以看出，当卷积神经网络使用分组码处理样本标签，并结合sigmoid激活函数和交叉熵计算训练过程中的反馈误差时，同样具备权重和偏置的更新快慢与反馈误差大小保持一致这一特性.因此，本文选择这一组合作为验证本文算法的另一种反馈损失计算方式.

3.3 用于图像分类的CNN结构

本文使用三种不同的卷积神经网络结构，并结合三种不同的数据集来验证CNN输出维度和标签集的最小码距对系统分类精度的影响.

图1和图2是ResNet卷积神经网络两种残差模块的网络结构.图3所示为本文仿真使用的三种CNN结构，每种网络结构对应使用图4的一种图像分类数据集.图3的(a)和(b)为一个二分类的卷积网络模型，这两个网络模型在LeNet网络的基础上进行了改进[8]，使得输出维度可以在2、10和20中进行选择，用于探究CNN输出维度与分类精度的关系.图3(c)为一个10分类的卷积网络模型，其在21层的ResNet网络的基础上改进而来，用来探究CNN标签集合的最小码距与分类精度的关系.

图1 恒等残差模块Fig.1 Constantresidualmodule图2 卷积残差模块Fig.2 Convolutionresidualmodule

图3 本文仿真所用CNN结构图Fig.3 CNN structure in simulation

4 实验结果及分析

4.1 数据集

本文的仿真实验使用了3个数据集(如图4所示)，分别作为图3的三种网络模型的训练和测试数据.图4(a)所示的Wider Faces数据集为32×32像素的RGB彩色图像，训练样本中人脸图片和非人脸图片各有15000张，测试样本中人脸图片和非人脸图片各有6000张.图4(b)所示的Dogs vs.Cats 数据集为64×64像素的RGB彩色图像，训练样本中猫狗图片各10000张，测试样本中猫狗图片各5000张.图4(c)所示的Cifar-10数据集为32×32像素的RGB彩色图像，数据集共10个类别，其中训练集有50000张图片，测试集有10000张图片.

4.2 验证输出维度对CNN性能的影响

图5所示仿真图探究了输出维度对卷积神经网络分类精度的影响.图5(a)为使用图3(a)所示网络模型，对图4(a)所示的Wider Faces数据集进行训练和测试所得到的仿真结果；图5(b)为使用图3(b)所示网络模型，对图4(b)所示的Dogs vs.Cats数据集进行训练和测试所得到的仿真结果；图5(c)为使用图3(c)所示网络模型，对图4(c)所示的Cifar-10数据集进行训练和测试所得到的仿真结果.

图4 部分图片数据集Fig.4 Partial image database

在图5(a)中，sigmoid-2、sigmoid-10和sigmoid-20所标记的曲线对应的模型在训练时都使用sigmoid激活函数和交叉熵损失函数计算反馈损失.三条曲线的不同之处在于，sigmoid-2曲线对应的CNN模型使用独热编码处理训练样本的标签，而sigmoid-10曲线和sigmoid-20曲线对应的模型使用分组码处理训练样本的标签.sigmoid-10曲线对应的模型使用(10，4)分组码，而sigmoid-20曲线对应的模型使用(20，4)分组码.softmax-2和softmax-20所标记的曲线对应的模型在训练时使用softmax激活函数和对数似然损失函数计算反馈损失.不同之处是，softmax-2曲线对应的模型使用独热编码处理训练样本的标签，而softmax-20对应的模型使用(20，4)分组码处理训练样本的标签.图5(b)和图5(c)中各条曲线所代表的含义与图5(a)类似，三幅仿真图的不同点在于图5(a)、图5(b)和图5(c)所使用的数据集和网络结构不同.表1是图5中每条曲线对应的最大准确率.

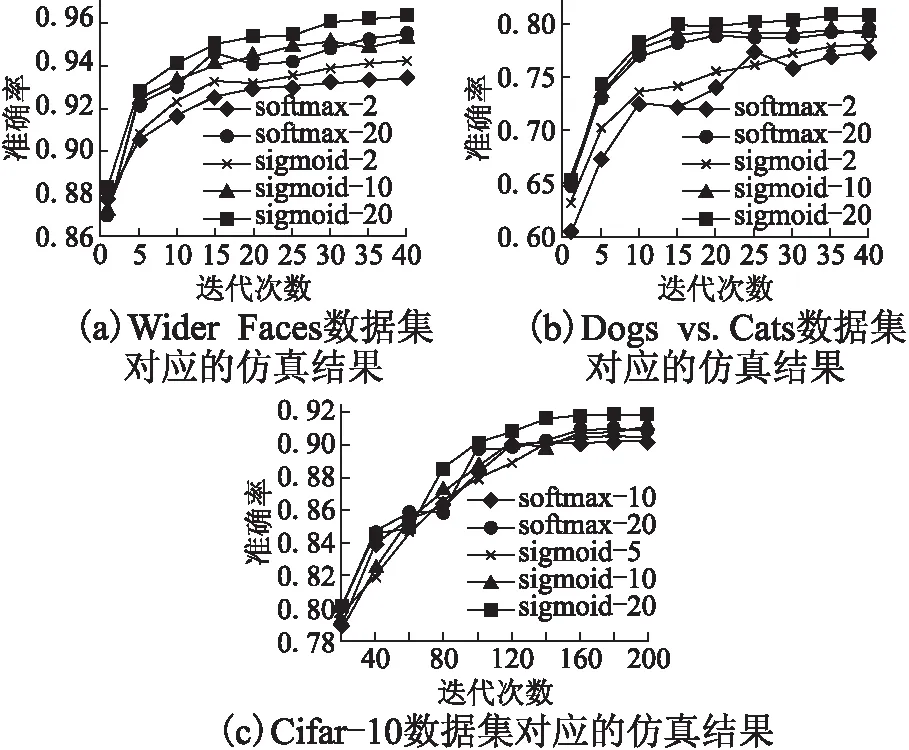
图5 输出维度对CNN性能的影响Fig.5 Simulation results in different output dimensions

从图5和表1中的sigmoid-2(sigmoid-5)、sigmoid-10和sigmoid-20，以及softmax-2(softmax-10)和softmax-20的对比分析中可以看出，当增加卷积神经网络输出维度时，卷积神经网络的分类精度会随之提高.同时从sigmoid-20曲线和softmax-20曲线的对比分析中还可以发现，当使用分组码处理训练样本的标签时，卷积神经网络的最后一层使用sigmoid激活函数比使用softmax激活函数对CNN的分类精度提高得更多一些.

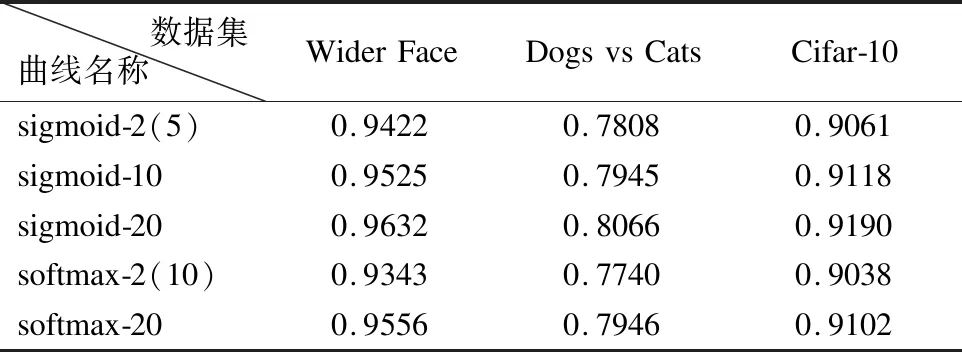
表1 图5所示曲线对应的最大准确率Table1 Maximum accuracy of each curve in Fig.5

4.3 验证标签的最小码距对CNN性能的影响

本文的4.2节探讨了CNN输出维度对分类精度的影响，接下来，图6所示的仿真图探究标签的最小码距对卷积神经网络分类精度的影响.

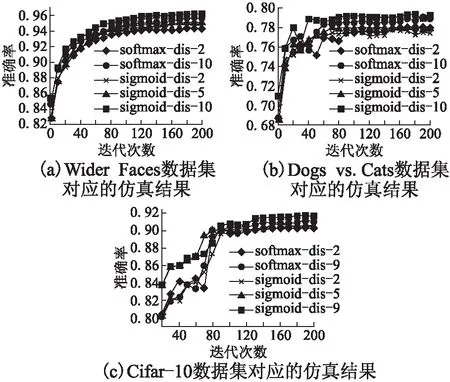
图6 标签的最小码距对CNN性能的影响Fig.6 Simulation results with different minimum code space

同图5类似，图6(a)为使用图3(a)所示网络模型，对图4(a)所示的Wider Faces数据集进行训练和测试所得到的仿真结果；图6(b)为使用图3(b)所示网络模型，对图4(b)所示的Dogs vs.Cats数据集进行训练和测试所得到的仿真结果；图6(c)为使用图3(c)所示网络模型，对图4(c)所示的Cifar-10数据集进行训练和测试所得到的仿真结果.并且图6(a)和图6(b)对应CNN的输出维度为10，图6(c)对应CNN的输出维度为20.图6中的softmax-dis-2和softmax-dis-10(9)所标记曲线对应的CNN模型在训练时都使用softmax激活函数和对数似然损失函数计算反馈损失，这两条曲线的区别在于softmax-dis-2曲线对应训练样本标签的最小码距为2，而softmax-dis-10(9)对应的训练样本标签的最小码距为10(9).sigmoid-dis-2、sigmoid-dis-5和sigmoid-dis-10所标记曲线对应的CNN模型在训练时都使用sigmoid激活函数和交叉熵损失函数计算反馈损失，区别在于sigmoid-dis-2曲线对应训练样本标签的最小码距为2，而sigmoid-dis-5曲线和sigmoid-dis-10曲线对应的训练样本标签的最小码距分别为5和10.为便于进行对比，表2列出了图6中各条曲线对应的最大准确率.

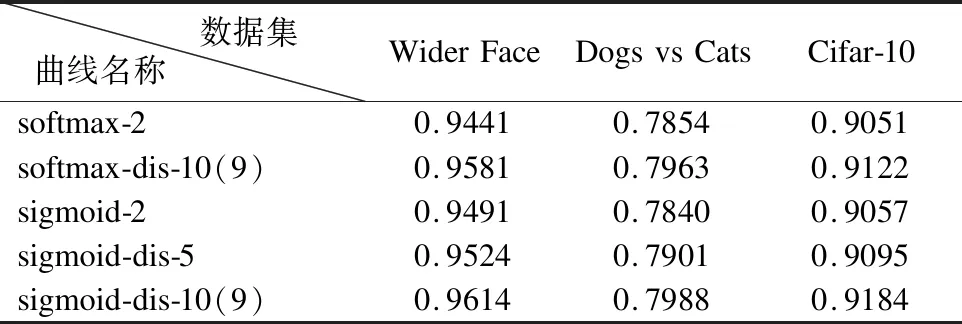
表2 图6所示曲线对应的最大准确率Table 2 Maximum accuracy of each curve in Fig.6

图6和表1证明，当增加训练样本标签的最小码距时，图像分类卷积神经网络的分类精度会随之提高.并且从图6(c)的sigmoid-dis-9曲线和softmax-dis-9曲线的对比中可以发现，当使用分组码处理样本标签时，使用sigmoid激活函数比使用softmax激活函数的效果更好，这与从图5的仿真结果中得出的结论是一致的.

5 结 语

本文提出通过增加图像分类卷积神经网络的输出维度，并使用最小码距更大的分组码代替独热编码处理训练样本的标签，同时利用sigmoid激活函数和交叉熵计算训练过程中的反馈损失.实验结果表明，改进后的CNN性能比传统中使用softmax激活函数结合对数似然损失函数计算反馈损失的CNN性能更好.但同时仿真结果也表明，相比于二分类任务，改进后的CNN对于图片的多分类任务的精度提高幅度要小一些，本文认为造成多分类任务性能提升不够显著的原因是没有选择最佳的标签组合方式.即对于不同的数据集，其最优的标签组合方式可能不同，在以后的工作中将考虑通过训练的方式获得最优的标签组合，以此提高改进CNN对图片的多分类任务的分类精度.