基于RVM机器学习方法的高校理论与实验教学质量评价模型

傅翠霞 罗亦泳

摘  要： 为提高高校理论教学与实验教学质量评价的精度及可靠性，基于机器学习新算法RVM构建高校理论教学与实验教学质量评价新模型。对RVM的核函数及参数确定方法进行改进，利用遗传算法优化的MK?RVM模型分别建立高校理论与实验教学质量评价的MK?RVM新模型，并构建基于置信区间的结果可靠性分析方法。实验结果表明，高校理论教学与实验教学质量评价MK?RVM模型的各项精度指标均表现优秀，精度等级达到“好”;训练集及测试集的教学质量评价真实值均在MK?RVM估计的95%置信度置信区间内，证实基于MK?RVM的教学质量评价结果具有较好的可靠性。因此，RVM算法为高校理论教学与实验教学质量评价提供了一种新的有效途径。

关键词： 相关向量机（RVM）; 教学质量评价; 精度分析; 可靠性分析; 遗传算法; 置信区间

中图分类号： TN911?34                        文献标识码： A                           文章编号： 1004?373X（2019）13?0181?06

Universities theoretical and experimental teaching quality evaluation model

based on RVM machine learning method

FU Cuixia1， LUO Yiyong1， 2

（1. College of foreign Languages， East China University of Technology， Nanchang 330013， China;

2. School of Geodesy and Geomatics， Wuhan University， Wuhan 430079， China）

Abstract： The new quality evaluation models of theoretical teaching and experimental teaching in universities are built on the basis of relevance vector machine （RVM） to improve the accuracy and reliability of the quality evaluation of theoretical teaching and experimental teaching in universities. The kernel function and parameter determination method of RVM are improved， and the MK?RVM model optimized by genetic algorithm is established. The new MK?RVM models for quality evaluation of theoretical teaching and experimental teaching in universities are set up respectively， and the result reliability analysis method based on confidence interval is constructed. The experimental results show that all the precision indicators of MK?RVM model based quality evaluation of theoretical teaching and experimental teaching in universities are excellent， and the precision level can reach up to "good". The real values of teaching quality evaluation of training set and test set are within the 95% confidence interval of MK?RVM estimation， which confirms that the MK?RVM based evaluation result of teaching quality has high reliability. Thus， the RVM algorithm provides a new effective way for the quality evaluation of theoretical teaching and experimental teaching in universities.

Keywords： relevance vector machine; teaching quality evaluation; precision analysis; reliability analysis; genetic algorithm; confidence interval

0  引  言

众所周知，教学质量评价是高校进行教学质量监控与管理的核心内容。通过建立一套科学、合理、可靠性高的教学质量评价方法，能及时发现教学过程中存在的问题，为高校教学质量管理部门制定相应措施提供可靠的依据，是提高教学质量的重要保障。

教学质量评价方法构建主要包括评价指标体系及评价模型的建立。当前，国内外学者针对课堂教学质量评价指标体系开展大量研究，已经建立了较为完善、有效的评价指标体系[1?4]。由于教学包含教与学的动态过程，影响教学质量的因素众多，课堂理论教学与实验教学是高校教学体系中的两大重要组成部分。

近年来，课堂理论教学与实验教学质量评价模型较多，高校通常采用绝对评估法、评等法、相对评估法、评语法和综合评分法等方法，这些方法操作起来简单。但是方法过于主观，并且基于各评价指标和教学效果之间的线性关系，与教学质量评价是一个多因素影响下的复杂非线性问题这个事实不符[4?7]。因此，这些方法的评价结果与教学质量真实状况之间存在较大差异。当前，加权平均法、单项因子评价法、模糊聚类分析法、多元线性回归、层次分析法、灰色关联法等方法在教学质量评价中得到了一定的应用，并取得了一定的效果[8?11]。但是这些方法仍然存在定权难、人为主观因素强、随意性大、不能描述非线性问题等情况，制约了这些方法的推广与使用。

随着人工智能算法——神经网络的发展与推广，许多学者开展神经网络应用于教学质量评价方面的研究，并比传统方法取得了更好的效果 [12?16]。但神经网络算法结构设计困难，容易陷入局部最优，小样本时算法结果不稳定，并且其理论基础还不够完善。针对BP神经网络的缺点，支持向量机算法被用于课堂教学质量评价，评价精度得到一定的提高，但该算法的核函数及参数确定较为困难[17]。

综上所述，以上评价模型研究重点在于提高评价精度，而对于结果的可靠性未做分析，严重制约了评价模型的实际应用推广，并且模型本身存在较多有待解决的理论难点问题。

教学质量评价模型建立即构建教学质量评价指标与教学效果之间的函数关系。本文针对教学质量评价模型存在的问题，引入机器学习新方法——相关向量机（Relevance Vector Machine，RVM）算法。基于改进RVM构建教学质量评价指标与教学效果之间的复杂函数关系，从而分别建立课堂理论教学与实验教学质量评价新模型。基于RVM建立教学质量结果不确定性分析的置信区间分析方法，有效弥补当前教学质量评价模型无结果可靠性分析功能的缺点。通过对RVM方法评价结果的精度分析与不确定性分析，研究新模型的有效性及可靠性，为教学质量管理提供可靠的理论与实践依据。

1  相关向量机算法原理及改进

RVM算法具有运算简单、收敛速度快、精度高、参数少、高稀疏性等特点，核函数不受Mercer条件限制，计算过程及结果均具有概率解释，可分析结果的可靠性。基于RVM的以上优点，RVM模型在模式识别、图像分类、复杂系统拟合等领域得到很好的应用，但在教学质量评价方面未见相关研究成果。

为了提高RVM算法的精度及可靠性，对RVM进行理论改进，基于组合核函数构建多核函数相关向量机（MK?RVM）算法，提高算法的精度。利用遗传优化算法优化MK?RVM算法的参数，实现MK?RVM算法最优参数自动确定，减少由于参数不合理对预测精度的影响。

1.1  MK?RVM原理

对于RVM回归算法，设训练样本集为[xi，tini=1]，[xi]为输入向量， [ti]为目标值，[n]为训练样本数。假设目标[ti]独立，包含噪声[εi]，并且[εi～N（0，σ2）]，[σ2]为[εi]的方差，RVM回归模型可表示为：

1.2  基于遗传优化算法的MK?RVM参数优化

鉴于遗传算法在模型参数优化方面应用的广泛性及具有较好的全局最优能力，将遗传算法用于优化MK?RVM的参数。由式（4）可知，MK?RVM需要优化的参数包括[[λ1，λ2，ψ1]]。本文利用HIOA优化MK?RVM的3个参数。基于留一交叉验证法构建个体适应度计算函数[f（x）]，设置遗传算法的相关参数，具体步骤如下：

1） 设置遗传算法参数（群体大小[M]，终止代数[T]，交叉概率[Pc]，变异概率[Pm]）。一般[M]大小应在20～100，[T]取100～1 000，[Pc]取值在0.40～0.99，[Pm]取值在0.000 1～0.1。

2） 设定MK?RVM的参数[[λ1，λ2，ψ1]]的搜索范围。

3） 对参数进行编码（采用浮点数编码方法）。

4） 随机生成[M]个初始群体pop（[t]），[t=1]。

5） 根据个体适应度评价函数[f（x）]计算出第[t]代群体pop（[t]）的个体适应度。

6） 利用遗传操作中的选择算子（采用比例选择算子）确定父代个体遗传到子代的个数，通过选择可以得到新的群体newpop（[t]）。

7） 基于群体newpop（[t]），通过交叉（利用单点交叉算子以概率为[Pc]）生成新的群体crosspop（[t]）。

8） 基于crosspop（[t]），通过变异（利用基本变异算子以概率为[Pm]）生成新的群体mutpop（[t]）。

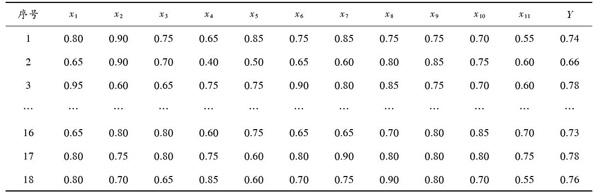
9） 判断优化是否停止。当[t

10） 利用[f（x）]计算mutpop（[t]）的个体适应度，并选取适应度最佳的个体，对该个体进行解码，获得MK?RVM的最优参数，实现参数自动确定，提高算法精度。

2  教学质量评价RVM模型构建及分析

基于RVM的改进算法MK?RVM分别建立课堂理论教学质量评价模型、实验教学质量评价模型。利用测试数据分析评价结果的精度与可靠性，验证新方法的可行性及可靠性。

2.1  课堂理论教学质量评价模型及分析

本文通过参考文献[1，3，4，14]确定11个课堂理论教学质量评价指标，包括：教学目的明确（[x1]）、重点难点突出（[x2]）、讲授知识科学（[x3]）、启发性教学（[x4]）、学习方法指导（[x5]）、教学手段丰富（[x6]）、教学态度严谨（[x7]）、教学内容精通（[x8]）、上课不迟到不拖堂（[x9]）、教学目标实现（[x10]）、重视学生反馈（[x11]），教学质量（[Y]）。高校教学质量评分表，请教学专家、相关教师、听课教师和上课学生对上课教师进行打分，然后选取打分比较一致的评价样本作为案例。收集18个样本，具体样本数据如表1所示。

表1 课堂理论教学质量样本数据

表2  课堂理论教学质量评价结果

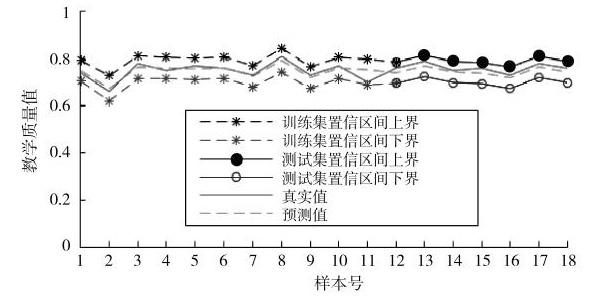
图1  预测结果置信区间分析（一）

表4  测试数据集精度评价（一）

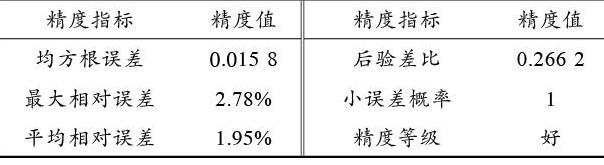
表3 精度等级划分

由精度指标表4可知，均方根误差、最大相对误差、平均相对误差、后验差比、小误差概率等精度指标表现优秀，并且根据后验差比、小误差概率确定预测结果精度等级为“好”，验证了课堂理论教学质量评价MK?RVM模型具有较高的精度。由预测结果置信区间分析图1可知，训练集及测试集的教学质量评价真实值均在MK?RVM估计的95%置信度的置信区间内，证实了预测结果具有较好的可靠性。

2.2  实验教学质量评价模型及分析

参考文献[2，13，14]和教育部《高等学校专业实验室评估标准》等资料确定实验教学质量评价指标，包括：教师素质、教学态度、教学设计、教学内容、教学方法、教学能力、教学效果、实验教学质量[Y]。高校教学质量评分表，请教学专家、相关教师、听课教师和上课学生对上课教师进行打分，然后选取打分比较一致的评价样本作为案例。搜集24个样本数据，具体数据如表5所示。取前[23]组数据作为训练数据，后[13]组数据作为测试集。以7个指标为输入，教学质量为输出，MK?RVM算法利用遗传算法对训练数据进行学习，确定最优参数为[[109.87，1.67，0.250]]。基于最优参数MK?RVM自动解算内部各类相关参数，建立实验教学质量评价模型。

表5  实验教学质量样本数据

基于以上建立的实验教学MK?RVM模型，对训练集与测试集中的教学质量进行预测，具体预测结果如表6及图2中的预测值所示。基于测试结果，统计各项精度指标如表7所示。

图2  预测结果置信区间分析（二）

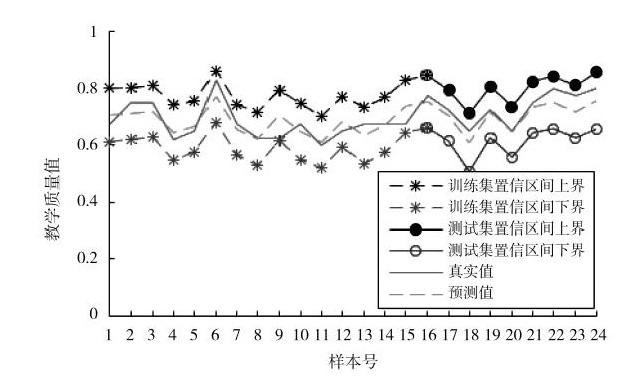
表6  实验教学质量评价结果

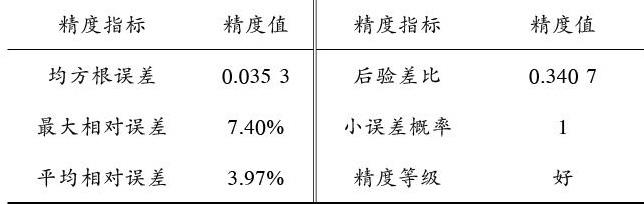
表7  測试数据集精度评价（二）

基于MK?RVM估计预测结果的方差，并计算对应95%置信度的置信区间，绘制置信区间分析图，如图2所示。

由精度指标表7可知，实验教学质量评价MK?RVM模型预测的各项精度指标表现优秀，精度等级达到“好”级，对实践教学质量评价具有较高的精度。图2可知，训练集及测试集中的教学质量真实值均在相应的95%置信度的置信区间内，证实结果可靠性高。因此，新方法适用于实践教学质量评价。

3  结  论

本文建立组合核函数及遗传算法优化参数的方法改进RVM，并基于该算法分别建立课堂理论教学质量评价模型及实验教学质量评价模型，通过实例数据分析新方法的精度及可靠性。

1） 在精度方面，基于RVM的课堂理论教学质量评价模型及实验教学质量评价模型的均方根误差、最大相对误差、平均相对误差、后验差比数值均较小，小误差概率均达到1。根据后验差比、小误差概率评定课堂理论教学质量评价模型及实验教学质量评价RVM模型精度等级均达到“好”级。

2） 在结果可靠性方面，基于RVM的课堂理论教学质量评价模型及实验教学质量评价模型估计结果的置信区间，并且其训练集及测试集的教学质量真实值均在对应的95%置信度置信区间内，证实了预测结果的可靠性。因此，基于RVM可构建精度较高、可靠性好的课堂理论教学质量评价模型及实验教学质量评价模型。

参考文献

[1] 郑延福.本科高校教师教学质量评价研究[M].徐州：中国矿业大学出版社，2012.

ZHENG Yanfu. Study on teaching quality evaluation of undergraduate college teachers [M]. Xuzhou： China University of Mining and Technology Press， 2012.

[2] 高建明.高校實验教学质量评价体系的建设与实践探索[M].长春：吉林人民出版社，2017.

GAO Jianming. Construction and practice exploration of experimental teaching quality evaluation system in Universities [M]. Changchun： Jilin People′s Press， 2017.

[3] 蔡红梅，许晓东.高校课堂教学质量评价指标体系的构建[J].高等工程教育研究，2014（3）：177?180.

CAI Hongmei， XU Xiaodong. Construction of quality evaluation system of classroom teaching in colleges and universities [J]. Higher engineering education research， 2014（3）： 177?180.

[4] 吴虹.基于模糊综合评判法的高校教师教学质量评价体系的构建[J].统计与决策，2010（3）：166?168.

WU Hong. Construction of teaching quality evaluation system of university teachers based on fuzzy comprehensive evaluation method [J]. Statistics and decision， 2010（3）： 166?168.

[5] 柳春.基于AHP法的成人学历教育教学质量评价体系研究[J].成人教育，2016，36（3）：64?68.

LIU Chun. Research on teaching quality evaluation system of adult education based on AHP method [J]. Adult education， 2016， 36（3）： 64?68.

[6] 徐卫国，吴刚.基于灰色系统理论构建军队院校教学质量评估模型[J].数学的实践与认识，2010，40（1）：53?61.

XU Weiguo， WU Gang. Establishment of military academy teaching quality evaluation model based on grey system theory [J]. Journal of mathematics in practice and theory， 2010， 40（1）： 53?61.

[7] 胡帅，姜华，曲巍巍.多元统计分析在外语教学质量评价中的应用[J].现代电子技术，2015，38（15）：126?132.

HU Shuai， JIANG Hua， QU Weiwei. Application of multiva?riate statistical analysis in foreign language teaching evaluation [J]. Modern electronics technique， 2015， 38（15）： 126?132.

[8] 辛建英.改进神经网络的大学物理实验教学质量评价[J].现代电子技术，2017，40（15）：146?149.

XIN Jianying. Improved neural network based teaching quality evaluation of university physics experiment [J]. Modern electronics technique， 2017， 40（15）： 146?149.

[9] 朱娅妮.基于智能优化算法的教学质量评价方法[J].杭州电子科技大学学报，2014，34（6）：66?70.

ZHU Yani. Teaching quality evaluation based on intelligent optimization algorithms [J]. Journal of Hangzhou Dianzi University， 2014， 34（6）： 66?70.

[10] 常宁.基于Elman神经网络的实验教学质量评价模型[J].中国人民公安大学学报（自然科学版），2014，20（3）：87?89.

CHANG Ning. Experimental teaching quality evaluation model based on Elman neural network [J]. Journal of Chinese People′s Public Security University （Natural science）， 2014， 20（3）： 87?89.

[11] 董薇.高校实验教学质量评价探究[J].黑龙江教育（高教研究与评估），2016（5）：52?53.

DONG Wei. Research on the quality evaluation of experimental teaching in colleges and universities [J]. Heilongjiang education （Higher educational research and evaluation）， 2016（5）： 52?53.

[12] 班丽丽，纪二娟.支持向量机的远程教学质量评估模型[J].现代电子技术，2017，40（13）：126?129.

BAN Lili， JI Erjuan. The distance teaching quality evaluation model based on SVM [J]. Modern electronics technique， 2017， 40（13）： 126?129.

[13] GUO S， ZHAO H， ZHAO H. A new hybrid wind power forecaster using Beveridge?Nelson decomposition method and relevance vector machine optimized by ant lion optimizer [J]. Energies， 2017， 10（7）： 1?6.

[14] ANDRIYAS T， ANDRIYAS S. Use of multivariate relevance vector machines in forecasting multiple geomagnetic indices [J]. Journal of atmospheric and solar?terrestrial physics， 2017， 154： 21?32.

[15] MARTINO L， VICENT J， CAMPS?VALLS G. Automatic emulation by adaptive relevance vector machines [C]// 2017 Scandinavian Conference on Image Analysis. [S.l.]： Springer， 2017： 443?454.

[16] 雷英杰，张善文.Matlab遗传算法工具箱及应用[M].西安：西安电子科技大学出版社，2014.

LEI Yingjie， ZHANG Shanwen. Matlab genetic algorithm toolbox and its application [M]. Xian： Xidian University Press， 2014.

[17] 罗亦泳，张豪.基于自适应进化相关向量机的耕地面积预测模型[J].农业工程学报，2015，31（9）：257?265.

LUO Yiyong， ZHANG Hao. Prediction model for cultivated land area based on self?adaptive differential evolution and relevance vector machine [J]. Transactions of the Chinese society of agricultural engineering， 2015， 31（9）： 257?265.