基于STEM理念的小学数学“综合与实践”整合设计
2019-07-08江澜
江澜
《义务教育数学课程标准(2011年版)》指出:“综合与实践”内容设置的目的在于培养学生综合运用有关的知识与方法解决实际问题,培养学生的问题意识、应用意识和创新意识,积累学生的活动经验,提高学生解决实际问题的能力。小学数学“综合与实践”的综合性不仅表现为数学内部各领域间的综合、数学与其他学科的综合、数学与学生日常生活的综合,也体现在解决问题的过程中要求学生的各种能力、各种方法、各种工具的综合。其使命在于给学生一个综合应用所学数学知识、方法,去实际解决一个数学内部或生活问题的机会,它的教育价值取向正与STEM理念相一致。
【教学目标】
1. 通过测量竹竿影子长度的实践活动,主动探索、掌握影子长度与目标物实际高度之间的比例关系。
2. 通过合作探究的方式,利用发现的规律解决“大树有多高”问题,设计测量金字塔高度的方案。
3. 在解决问题过程中,感受数学与科学、工程、技术的密切联系,进一步激发学习数学的兴趣,培养创新精神和问题解决能力。
【教学重难点】
沟通数学与科学的知识联系,综合运用多学科知识和方法,系统地经历解决问题的过程——设计、表达、实践、检验、反思、调整。
【教具准备】
课前:米尺,卷尺,计算器,纸笔,竹竿若干组(每组竹竿1米、50厘米各一根,另外两根长度不限),小木棒若干。
课堂上:小木棒若干、手电筒、尺子、纸笔、计算器。
【课前预习】
一、测影长
1. 六人一组,将班级分成若干组。
2. 每组2把卷尺和1组竹竿。另备好计算器、纸和笔。
3. 测前思考:为了能使测量的数据尽量精确,测量时应该注意些什么?
如:竹竿不能倾斜,要与地面垂直;手扶竹竿,不能放在竹竿的顶端,否则会影响影长的数据;身体不能挡住竹竿的影子;等等。
4. 各小组自选一个地点,把几根长度不同的竹竿直立在地面上,量出此时每根竹竿的影长,记录在表里,并计算比值。(测量时都取整厘米数,竹竿长与影长的比值保留两位小数)
完成测量记录单(要求填写各组竹竿长、影长、竹竿长与影长的比值等数据)。
二、搭支架
参考金字塔图片,用小木棒等搭建金字塔的支架模型。
设计意图:将“综合与实践”的教学活动仅当成一节课,这样的理解是狭隘的,实施是单一的。尝试以“长作业”的形式实施“综合与实践”活动,能够使课堂上的探究时间更加充裕。课前先让学生进行不同长度竹竿的影长测量、比值计算,以及用小木棒等搭建金字塔的支架模型,有助于课堂上集中時间和精力探究数学问题。
【教学过程】
一、知识唤醒,打通联系
观看三组图片:(1)两个身高不同的学生走在路上,投下了长短不同的两个影子。(2)阳光下物体的影子在一天中的变化。(3)某天早上九点时,1米长的竹竿在不同地点的影子。
师:我们在科学课上学习了影子的知识,说一说这三组图片中蕴含的影子知识。
引导学生总结:(1)学生通过观察个子高,影子就长;个子矮,影子就短,初步感知影长和身高之间存在一定的规律(正比例)。(2)物体的影子在一天中有方向和长短的变化,当光线与水平线的夹角为直角时,影子的长最短,当光线与水平线的夹角越来越小时 ,影子的长度越来越长 。(3)同一时刻,不同地点的影子长度不同。
设计意图:在五年级科学课上,学生已学习了太阳和影子的科学知识,本环节唤醒学生大脑中与影子相关的科学知识,为沟通本课主题、解决问题做好准备。
二、交流数据,发现规律
各小组交流汇报课前测量的数据。
师:为什么同样长的竹竿大家量出的影长却不同?
说明:因为各组测量的时间、地点可能不同,所以同样高度的直立竹竿的影长也在发生变化。
师:比较求得的比值,你有什么发现?
小组讨论、合作交流,从而发现规律:在同一地点,同时测量不同的竹竿,高度与影长的比值是相等的。
三、深入探究,理解本质
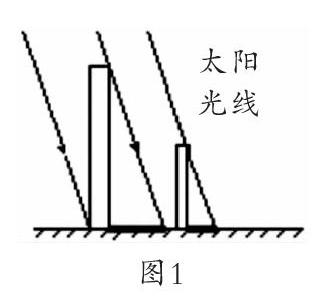
1. 课件呈现测量情境示意图(图1)。
师:把不同长度竹竿端点和各自的影子端点连起来,有什么发现?
生:形成了几个直角三角形,它们形状一样,但大小不一样。
课件动态演示把两个直角三角形相应的角重叠。
师引导:这两个直角三角形对应角分别相等,其实,这样的三角形关系,叫作相似三角形,到了中学会深入研究它们。相似三角形一个重要的特征就是对应的边长比值相等,所以我们大多数小组计算出的不同竹竿的长度与影长的比值是相等的。
反思:为什么有的组计算出的结果却不是完全一样的呢?可能是什么原因?
(如:竹竿不垂直,测量数据有误差,没有在同一时刻,等等。)
2. 师:根据上面的发现,猜想一根3米长的竹竿,当时直立在地面上的影长是多少?
设计意图:学生通过观察每组求得的比值,分析讨论,发现规律:在同一地点,同时测量不同的竹竿,高度与影长的比值是相等的。发现规律后,教学并未止步。笔者通过形象图示和直观演示,将该部分知识与中学的相似三角形知识联系,使学生了解规律背后的数学知识本质。学生在反思计算结果不一致的过程中,积累了实际操作的经验,因此对规律的理解更深入,为后续运用规律解决问题提供理论支撑和操作经验支撑。让学生进行规律的逆向运用,发展学生的思维能力。
四、设计实施,解决问题
1. 挑战1:大树有多高?
(1)出示问题:根据上面的发现,能算出学校里这棵大树的高度吗?
小组交流合作:应该准备哪些工具?需要测量哪些数据?测量时有哪些注意点?
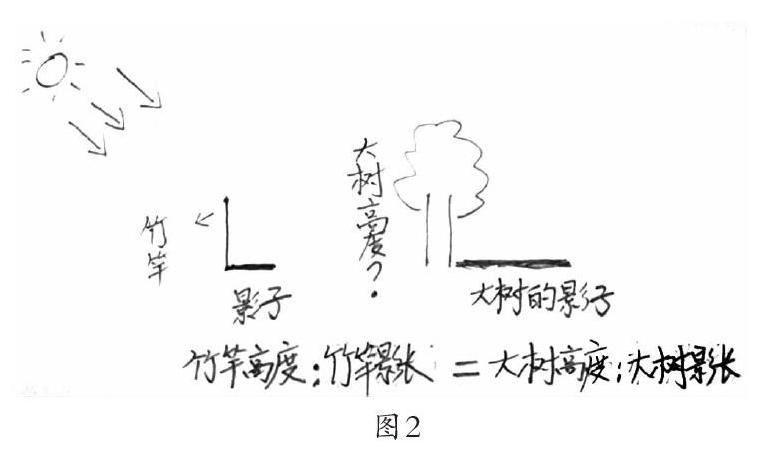
画出测算情境示意图。(图2)
学生在小组交流后明确:在计算时,可以先算出竹竿长与影长的比值,再运用比值求出大树的高度。
师:在测量竹竿的影长之后,如果过了一段比较长的时间,再去测量大树的影长。那么,这样计算出的结果还准确吗?为什么?
(2)出示具体情境进行计算。
如果某一时刻,身高1.6米的小丽在阳光下的影长为2.5米,一棵大树的影长为5米,那么大树的高度是多少?
设计意图:让学生利用发现的规律测量大树的高度,在问题解决的过程中采用小组合作探究的方式,以三个探究问题作为脚手架——“应该准备哪些工具”“需要测量哪些数据”“测量时有哪些注意点”,并要求学生画出示意图,将测量的方法外显为直观方式,整个合作探究过程重视培养学生思考的有序性、逻辑性、严谨性,以及思维表达能力。
2. 挑战2:金字塔有多高?
课件展示:金字塔是世界八大奇迹之一。看着这一巍峨的建筑,很多人都不禁猜测它到底有多高。但当时没有先进的测量仪器直接测出金字塔的高度,你能根据今天所学,设计出测量金字塔高度的方案吗?
(1)在设计前,我们先来看看哪条是金字塔的高?
明确:金字塔的高是指从金字塔顶点向底面作的垂线。
(2)小组合作探究。
①设计测量方案(重点写出所需工具及用途,需要测量的教据,测算步骤,注意点),画出测算过程示意图。
②以课前制作的金字塔支架模型为测量对象,选用合适的工具(如手电筒),进行现场模拟测量(根据问题情境,不能直接测出金字塔的高度,金字塔框架各边长可以直接测量)
(3)修改调整。
根据设计方案测算出金字塔模型的高度后,直接測量模型的高度,通过对比实际高度与测算结果,检验测算方案是否科学合理,进行方案的修改调整。
设计意图:在STEM教育中,整合和设计必不可少。从教育科学原理的角度来说,STEM教育要培养的是学生的迁移能力,引导学生能够把一个情境中学到的知识运用到另一个情境中。在“大树有多高”的问题解决之后,让学生进入“金字塔有多高”这个问题情境,通过合作探究的方式运用知识和方法迁移,进行方案设计和现场模拟测算,在解决过程中,学生需要综合运用多学科知识和方法。如设计和测算中需要运用数学的比例知识、流程图设计以及直观图示的方法,在实施操作中需要控制光源与水平线的夹角来调整影子的方向和长度。活动中注重学生系统地经历解决问题的过程——设计、表达、实践、检验、反思、调整,发展学生的多学科知识整合运用能力以及逻辑思维能力,强调成长型思维模式的培养。
五、微课延伸,拓展思考
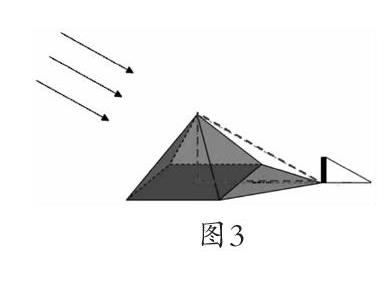
1. 观看内容为泰勒斯借助太阳光线测量金字塔高度的微课。(图3)
2. 对比反思。
你们的设计方案和泰勒斯的方法一样吗?存在什么共同点和不同点?
核心问题①:为什么计算时要用金字塔底面边长的一半加上外面的影长?
核心问题②:为什么泰勒斯要等到他的影长与身高相等时再去测量金字塔的影长呢?
生反馈:金字塔底面边长的一半加上外面的影长才能和金字塔的高构成一个直角三角形,才能利用相似三角形的边的比例关系计算出金字塔的高度;当泰勒斯身高与影长相等时,身高与影长的比值是1,这时金字塔高度与金字塔影长的比值也是1。所以,金字塔的高度等于金字塔影子的长度加上底面边长的一半,省去了计算环节。
设计意图:观看内容为泰勒斯利用太阳的光线测量金字塔高度的微课,让学生亲历经典数学问题的解决,而后引导学生对比和反思自己设计的方案和泰勒斯的方法有哪些相同点和不同点,见贤思齐,得到进一步优化思维方式的机会。
(作者单位:福建省厦门市松柏小学 责任编辑:王彬)
