电动拖拉机永磁同步电机控制系统建模仿真
2019-07-08李宇翔施爱平李福强
李宇翔 施爱平 李福强


摘要:永磁同步电机作为电动拖拉机上主要的动力电机有很好的应用前景。针对传统PID(比例-积分-微分)控制策略对电机转速控制的响应速度慢、控制精度低的缺点以及Matlab软件自带电机模块的局限性,提出模糊PI自适应控制策略并在电机数学模型的基础上创建了自定义永磁同步电机(PMSM)模块,通过Matlab & Simulink仿真软件,在永磁同步电机矢量控制系统中进行仿真分析。通过对参数的调节得出了理想的输出曲线,验证了永磁同步电机模型的合理性、先进性及其控制算法的有效性,为永磁同步电机控制系统设计和电机的调试提供了理论基础和新的思路。
关键词:永磁同步电机;矢量控制;模糊PI;建模仿真;Matlab & Simulink
中图分类号: S219.4;TM341 文献标志码: A 文章编号:1002-1302(2019)10-0224-06
电动拖拉机因其环保、低噪音和操作简单的特性成为当前农业装备研究的重点。其中的永磁同步电机的建模和仿真是整机控制的基础和关键。1831年巴洛发明了世界上第1台永磁同步电机。1983年价格低廉的铷铁硼永磁材料出现后,永磁同步电机的性能也取得了很大幅度的提高,被广泛应用于工农业领域中。随着电力电子技术的进一步发展,永磁同步电机因其体积小、转矩大、结构简单、可靠性高等特点成为了电动拖拉机一个可靠的选择[1-3]。我国稀土资源储量丰富,尤其是铷铁硼永磁材料的年产量居世界第一,因此,我们应该大力推动我国稀土产业和永磁同步电机技术的快速发展,以达到减排、保护环境,实现可持续发展,研究永磁同步电机及其控制策略具有重大意义,而建立数学模型并利用计算机仿真技术来研究已成为其研究的主要方法之一。
在矢量控制的众多方法中最为简单的研究方法是令 id=0(id为d轴上的电流分量),在Matlab & Sumilink平台下建立仿真模型并进行仿真,并对仿真结果进行分析。该模型的建立和分析对电机的实际控制及其在电动拖拉机中的应用提供了新的研究思路。
1 永磁同步电机数学模型
以两相导通星形三相六状态为例,建立永磁同步电机(PMSM)的数学模型并且分析其电磁转矩等特性。实际的永磁同步电机的电磁关系非常复杂,为了方便对模型的分析和控制策略的研究,对模型进行简化分析,并作出如下假设:(1)忽略电机中铁芯磁路饱和,即忽略电流变化大小对电感参数的影响;(2)不计永磁同步电机磁滞损耗和涡流损耗;(3)定子绕组三相对称,转子的磁场在空间呈正弦分布;(4)驱动二极管和续流二极管为理想元器件;(5)转子上无阻尼套组。
经过坐标变换:将三相静止坐标a-b-c变换到两相静止坐标α-β的变化叫作克拉克(Clark)变换,将两相静止坐标α-β变换为两相旋转坐标d-q的变化叫做帕克(Park)变换。
2 基于Matlab的永磁同步电机矢量控制模型的建立
在充分分析了永磁同步电机数学模型的前提下,本研究决定采用id=0控制策略,使电机的转矩控制更加精准从而更好地控制定子电流和转子速度,构成电流环和速度环的双闭环结构。永磁同步电机的控制系统结构和系统模型分别见图1、图2。
基于矢量控制原理,利用Matlab & Simulink来对永磁同步电机进行建模仿真,根据模块化思想,可以把永磁同步电机矢量控制分为坐标变换模块、控制器模块、空间矢量脉宽调制(SVPWM)模块、逆变器模块和PMSM模块等。通过将这些模块的有机整合,可以建立PMSM的仿真模型,并且实现对PMSM的有效控制。
2.1 坐标变换模块
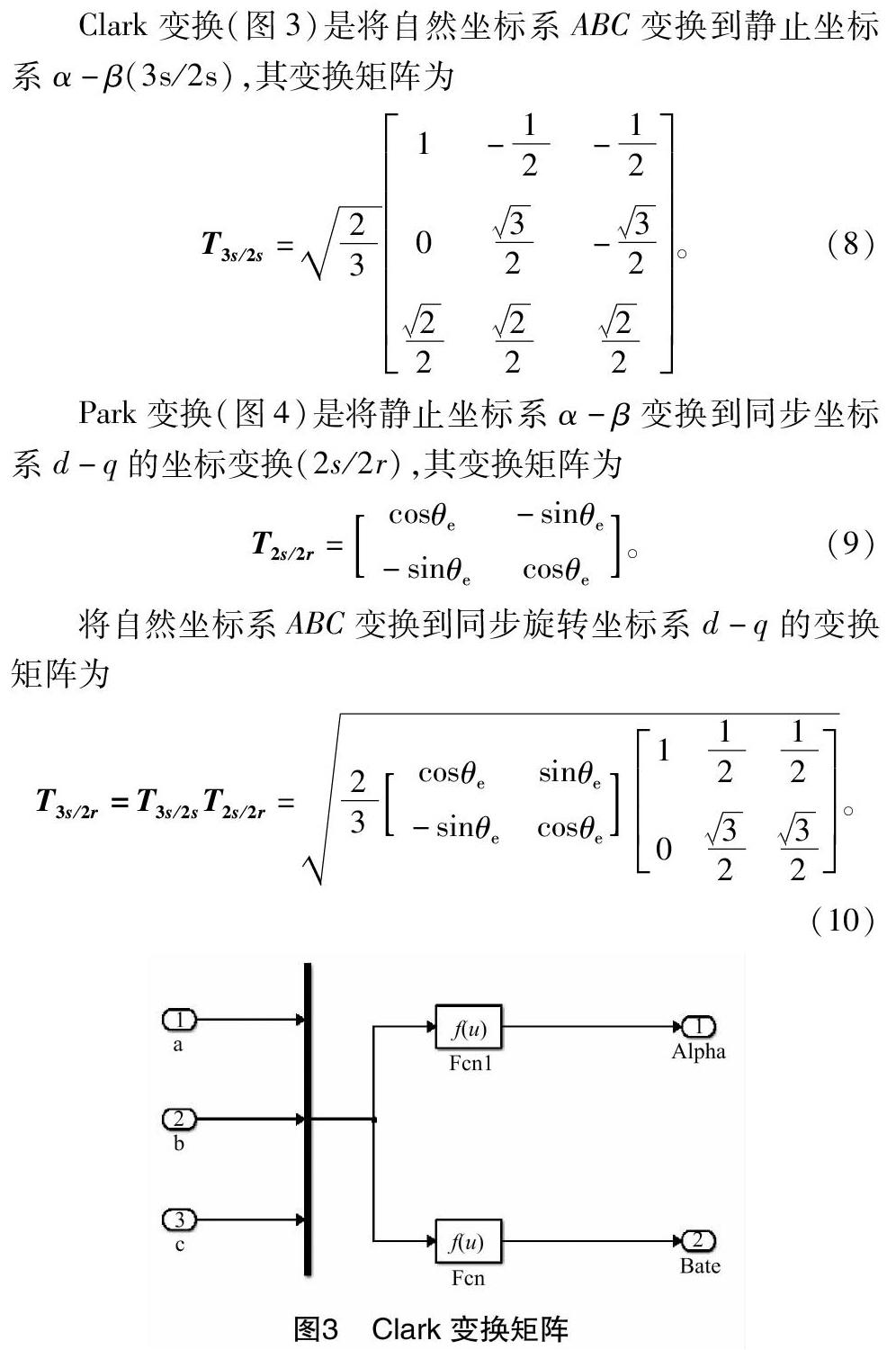
PMSM电机建模的坐标变换用到Clark变换和Park变换。其原理是坐标变换前后变换功率不变,合成磁动势也不变;作用是将比较复杂的三相静止坐标参数变换成比较简单易控制的两相旋转坐标参数,简化了控制方法和过程。交流电机经过Clark变换和Park变换后可以近似看作直流电机。
2.2 速度控制模块
PID(比例-积分-微分)控制器的传递函数为:
速度控制模块一般采用PI或PID控制方法,但是传统PID控制策略对电机转速控制的响应速度慢,控制精度低,以及电机调速系统负载或参数变化时很难达到预期效果。因此,本研究采用的是自适应模糊PI控制方法,因为该控制方法既具有模糊控制灵活、抗干扰能力强、适应性强和鲁棒性好的优点,同时兼具高精度控制,而且可以根据偏差和偏差变化率的不同,对参数自动进行在线整定[4]。速度环采用模糊PI设计的主要目的是为了使系统的反馈转速最大限度地跟随给定速度,响应速度快,且加强了其抗干扰能力。模糊PI的控制原理见图5。
自适应模糊PI系统是基于常规PI控制,通过模糊推理思想,将误差e和误差变化率ec作为模糊控制器的2个输入量,并通过其输出变量,利用模糊规则对PI参数进行实时修正,实现PI参数的最优化。由图5可知,根据经验值设定
Kp*和Ki*的值,然后由模糊推理可知修正值ΔKP和ΔKi,最后通过经验值和修正值得到最优Kp和Ki。其中Kp*和Ki*为经典PI的参数,而ΔKp和ΔKi是模糊PI修正值。设:
速度控制模块仿真见图6:
定义e和ec模糊子集为{NB(负大),NM(负中),NS(负小),ZO(零),PS(正小),PM(正中),PB(正大)},并将模糊子集映射到论域[-3,3]上。将模糊控制器输出的Kp*和Ki*作为经典控制器的比例、积分,2个参数的修正输入量重新参与系统的控制,定义其模糊子集为{NB,NM,NS,ZO,PS,PM,PB},將其论域映射到[-3,3]上。
模糊规则表的建立主要是通过操作者经验以及对系统运行和性能参数不断调试的经验总结[5]。针对输入量偏差e以及偏差的变化率ec的变化情况,根据表1和表2所示控制规则对ΔKp和ΔKi这2个参数进行在线调整,从而使得控制参数更为精准,同时也让控制系统拥有更加优秀的动静态性能[6]。
2.3 SVPWM模块
当笔者将3相对称正弦电流输入到电机中时,电机内部就会产生圆形磁链。SVPWM以其为基础,通过对逆变器开关的不同状态组合方式,得到8种逆变器开关模式,也就会得到8个基本电压空间矢量,从而产生有效矢量逼近基准圆[7]。在8种组合电压空间矢量中,包括6种非零矢量U1(001)、U2(010)、U3(011)、U4(100)、U5(101)、U6(110)和2个零矢量U7(111)、U0(000)。SVPWM技术通过以上6种基本电压空间矢量中的相邻有效矢量和零矢量,采用各自不同的作用时间来等效电机所需要的空间电压矢量。SVPWM算法模拟仿真模型见图7。
2.4 PMSM模块
在整个控制系统的仿真模型中,PMSM本体模块是最重要的部分,反映的是PMSM电机的本质属性,虽然Matlab & Simulink中的Sim Power System提供了按“Y”形连接的PMSM模块。如图8所示,PMSM模块共有4个输入端,其中前3个输入端,分别为A相、B相、C相,第4个输入端为转矩输入的端Tl。
但是随着技术的发展,仿真应用日益广泛而且功能要求不断提高,Matlab & Simulink中的Sim Power System提供的PMSM模块出现不足,在电机参数在线修改、坐标定义等方面不能满足仿真要求,给研究带来不便。例如在对PMSM的定子绕组电阻值做辨识研究时,因为温度的变化对电阻有一定的影响,所以模拟电阻随温度连续变化须要在线修改电阻值[8]。由于Matlab自带的PMSM模块不支持在线参数修改,使得类似的变参数仿真的变化量难以考察,从上述例子可知,建立拥有广泛适用性的电机模型是非常有必要的。因此笔者根据数学模型建立了自定义PMSM模块,使其在变参数变结构的动态仿真方面更加具有实际意义[9]。根据数学模型建立的PMSM模块见图9。
3 仿真分析
因为在永磁同步电机矢量控制中,大功率电机与小功率电机矢量控制模拟仿真系统的三相电流,转速和转矩波形曲线大致相同,所以本研究采用功率为2.2 kW的永磁同步电机。根据以上建立的PMSM仿真模型,在Simulink环境下运行电机并且进行该电机矢量控制模拟仿真测试,采用的电机参数如下:电机功率P=2.2 kW;直流电压Udc=550 V;定子绕组电阻Rs=2.875 Ω;d相绕组ψf=8.5×10-3H;q相绕组 Lq=8.5×10-3H;转子磁场磁通ψf=0.175 Wb;转动惯量J=0.8×10-3 kg/m;极对数np=4;B=0。为了验证该PMSM电机在Simulink环境下工作的动静态性能,让电机先空载启动,当电机进入稳态阶段时,在t=0.05 s时突然施加Tl=2 N·m 的负载并且在0.1 s时将电机转速由300 rad/min增加至3 000 rad/min。系统的三相电流、转速和转矩波形曲线如图10所示。
由图10-a可知,电机启动后在4.5 ms内转速快速上升,并迅速达到稳定状态转速300 rad/min,在0.1 s时电机转速经过0.04 s的加速上升由300 rad/min增至3 000 rad/min并且迅速达到稳定,由此可见电机动态响应性能良好。
由图10-b可知,PMSM空载转动时,电机启动阶段大约持续4.5 ms,并且这段时间电机转矩为 7.6 N·m;0.05 s 时,突然施加负载 Tl=2 N·m,电机经过短暂的波动迅速到达
2 N·m; 0.1 s时转速突变为 3 000 rad/min 经过0.04 s转矩由2 N·m上升为7.6 N·m。电机启动阶段和负载运行阶段,系统能够保持转矩的恒定,没有产生较大的转矩,参考电流限幅作用非常明显,但是由于启动阶段电机转子的磁场转速与定子的磁场转速不同,制动转矩在短时间内由定子磁链和永磁体磁链产生的转矩提供,当牵引转矩小于制动转矩时,不考虑电机内部摩擦转矩,电机总体转矩会迅速下降为0,从而产生波动;同理当转速突变为3 000 rad/min时,也会产生类似的波动。
由图10-c可知,三相点仅在启动阶段电流较大,在 4.5 ms后达到稳定状态,在0.05 s时施加2 N·m的负载,三相电流会快速响应,在短暂的波动后再次达到新的稳定状态;在0.1 s转速突变为3 000 rad/min时电流会再次迅速响应,在0.04 s后达到新的稳定状态。
由图10-a可知,电机启动阶段的转矩(转速变化量为300 rad/min)与电机转速突变时间段(转速变化量为 2 700 rad/min)所需要的转矩基本相同。如图11所示,本研究选取不同转速变化量(选取了300~5 000 rad/min 间的部分数据)并且测定相应的转矩发现:电机转速发生变化且转速变化量小于4 000 rad/min时,转矩曲线比较平稳,当转速变化量超过4 000 rad/min时,转矩将会逐渐减小;当转速变化量为5 000 rad/min时,转矩减小为0。当电机转速变化时,电机转子的磁场转速与定子的磁场转速不同,制动转矩短时间内由定子磁链和永磁体磁链产生的转矩提供,可以使转子磁场速度与定子磁场速度相同,当转速变化量超过 5 000 rad/min 时,电机无法提供对应的转矩,所以会造成电机丢步,如果持续时间较长,会对电机造成不可逆的损坏。
4 结论
本研究在基于Matlab & Simulink的基础上,搭建了整个永磁同步电机控制系统速度和电流双闭环仿真模型,电流控制和速度的控制分别由电流滞环控制和模糊PI自适应控制方法来实现。仿真结果表明,波形符合理论分析,系统的平稳性比较好,响应快,并且具有良好的动态效果和静态效果,符合永磁同步电机的运行特性,并且本研究讨论了转速变化量与转矩的关系,为矢量控制的实现提供了基础并为永磁同步电机的设计和调试提供了新思路。
参考文献:
[1]李崇坚. 交流同步电机调速系统[M]. 北京:科学出版社,2006.
[2]de Almeida A T,Ferreira F J T E,Fong J A C . Standards for efficiency of electric motors[J]. IEEE Industry Applications Magazine,2011,17(1):12-19.
[3]Wooldridge M,Jennings N R. Intelligent agents:theory and practice[J]. The Knowledge Engineering Review,1995,10(2):115-152.
[4]卞延慶,庄 海,张颖杰. 基于模糊PI的永磁同步电机矢量控制研究[J]. 微电机,2015,48(11):62-67.
[5]秦灿华,刘连根,曹 洋,等. MW级永磁同步电机无速度传感器矢量控制研究[J]. 湖南工业大学学报,2012,26(1):37-40.
[6]杨 勇. 基于模糊自整定的改进型永磁同步电机矢量控制仿真研究[J]. 机电工程技术,2010,39(8):47-49.
[7]白继荣,李桥梁,黎志光. 带转矩和磁链内环的交流异步电机矢量控制系统仿真[J]. 电机技术,2008,29(2):1-4.
[8]Wilson S D,Stewart P,Taylor B P. Methods of resistance estimation in permanent magnet synchronous motors for real-time thermal management[J]. IEEE Transactions on Energy Conversion,2010,25(3):698-707.
[9]王莉娜,杨宗军. Simulink中PMSM模型的改进及在参数辨识中的应用[J]. 电机与控制学报,2012,16(7):77-82.
