20世纪以来中国数学课程标准中算术与代数表征功能的变化及启示

沈 阳，张晋宇，李 娜，鲍建生



20世纪以来中国数学课程标准中算术与代数表征功能的变化及启示

沈 阳1，张晋宇2，3，李 娜1，鲍建生1，3

（1．华东师范大学 数学科学学院，上海 200241；2．华东师范大学 教师教育学院，上海 200062；3．上海市“立德树人”数学教育教学研究基地，上海 200241）

根据《20世纪中国中小学课程标准·教学大纲汇编（数学卷）》和21世纪以来的课程标准中算术与代数的内容，围绕数学表征的表达交流、操作转换、建模应用3种功能，采用历史研究方法，编码分析1902—2017年中国中小学数学课程文件（标准）中算术与代数表征的变化趋势．研究结果表明：数学表征的功能会随着课程标准的变化而变化，并且3种表征功能的侧重点和相互关联性在不同学段也有不同的特点．表达交流功能在小学阶段依赖于建模应用，而初高中阶段依赖于操作转换；操作转换功能在3个学段均处于主导地位；建模应用功能在小学、初中阶段并没有受到重视，而在高中阶段新课程改革后逐步受到重视．

数学表征；表征功能；算术；代数

1 引言

表征（representation）是认知心理学中的一个重要概念，意指知识在学习者头脑中的呈现和表达方式[1]．数学表征既可指人脑内部心智活动的表现，又可指思维活动的外在表现形式；既可指表达数学关系的过程，又可指数学关系的表达形式；既可指进行数学交流的工具，又可指进行数学交流的内容．而且数学表征有助于学生理解概念、关系或关联自己解决问题过程所使用的数学[2-3]，也有助于学生组织思维，更具体地认识数学概念及反思[4]，所以一直以来数学表征都受到国际上的普遍重视．比如丹麦KOM项目中将数学表征视为八大能力之一[5]，学生能力国际评价项目PISA（Program for International Student Assessment）在PISA2000—PISA2015都将数学表征作为数学能力之一[6-10]，全美数学教师理事会NCTM（National Council of Teachers of Mathematics）中将数学表征作为十大能力之一[4，11]．因此，依据《20世纪中小学课程标准·教学大纲汇编（数学卷）》，探讨数学表征随数学课程改革的历史演变，从中发现规律并寻求启示．

2 研究问题及方法

这里主要研究以下两个内容：一是构建数学表征功能的分析框架；二是考察20世纪中国中小学数学课程标准中数学表征的变化趋势及其成因．希望通过这一研究，发现数学表征在不同年代和不同学段的发展规律，为理解新课标及后续的修订提供参考．

采取的主要研究方法是“历史研究”（historical research）．历史研究法的目标是通过系统地搜索和组织数据，以更好地了解历史现象及其可能的因果关系[12]．一般历史研究的过程包括甄别史料来源，考证历史证据和解释历史数据3个步骤．因为中国是中央集权的国家，国家颁布的数学教学大纲，以及与之适应的考试大纲享有极高的权威[13]，而这里的研究对象为《20世纪中国中小学课程标准·教学大纲汇编（数学卷）》以及21世纪以来的课程标准，是国家给出的统一标准，故研究对象具有一定的可靠性，所以只进行第三个步骤．

在解释历史数据过程中采用质性研究和定量研究相结合的研究方法．定量研究是根据编码框架进行编码而获得数据，质性研究是解释定量研究的结果，这种方法被称为顺序—解释型研究设计（sequential-explanatory research design）[14]．故采用顺序—解释型研究设计法．

3 研究过程

3.1 数学表征概述及其功能性定义

数学表征内涵丰富且复杂[15]，一般从对数学知识的认知角度和数学表征的功能两个维度进行定义，而第一个维度大致集中在内部表征、外部表征及表征转换3个方面[16]．内部表征是指个体对所学知识的心理构造，一般不容易被观察到[17]，例如心理学认为知识表征指人在自己的工作记忆和长时记忆中对信息的储存、表示和再现方式[18–19]．外部表征是一种物理的、可观察的行为或对象，例如《数学教育百科全书》中描述数学表征是可见的、有形的产品，如图表、数字、图形、具体实物或教具、物理模型、数学表达式、计算机屏幕上的描述或者计算机编码等，代表数学思想和数学关系[20–21]．表征转换最初由Richard Lesh提到，后丹麦数学教育家Mogens Niss也强调其作用，认为数学表征能力是指理解、诠释和辨识数学对象、现象和情境的多种表征，能了解和使用表征之间的关系并掌握不同表征之间的优势和限制，能在各类表征中进行选择和转换[5，22]．徐斌艳等人对数学表征和转换能力分别定义，认为数学表征是用某种形式，如书面符号、图形（表）、情境、操作性模型、文字（包括口头文字）等，表达要学习的或处理的数学概念或关系，以便最终解决问题；数学转换能力是指在数学问题解决过程中，保持数学问题的某些不变性质，改变信息形态，将要解决的问题进行数学转化[16，23]．从功能角度出发，具有代表性的是NCTM中对数学表征的定义，美国NCTM在2000年出版的《学校数学教育的原则和标准》（）中，首次加入表征的标准，认为所有学生都能够创造和利用各种数学表征来组织、记录和交流数学观念，能选择、应用和互换各种数学表征方法解决问题，会应用表征模拟并解释物理社会和数学中的现象[4]．鲍建生等人通过Bruner和Lesh对表征类别归纳出两种功能：沟通工具以及思维的材料．作为沟通工具，是用特定的表征形式来描述活动经验；作为思维的材料，则是用表征来代表物化的数学概念或内蕴化的活动类型，对表征所代表的意义进行思维操作[17]．

“实用主义”不仅是中国数学的一大传统，而且也成为中国数学教学研究的一种重要的价值选择[24]，又由于课题需要，需要对《20世纪中小学课程标准·教学大纲汇编（数学卷）》和21世纪以来的课程标准（小学、初中包括01、11版，高中包括03、17版）的各学段以及各内容领域进行分析（这里只针对算术与代数部分），所以从表征功能的角度出发，对其教学内容进行分析，探索20世纪中小学算术与代数表征的发展趋势，试图从中得到一些启示．上述文献中鲍建生总结的两种表征的功能其实可以归纳为表达交流和操作转换，NCTM中还描述了建模应用功能．在此基础上，将表征从功能的视角分为表达交流、操作转换和建模应用，表达交流功能是指利用符号（书面符号、口语表达）以及图形图表进行沟通，操作转换功能是指计算（度量）、逻辑推理的思维操作或实物（算盘）、计算机（计算器）等模型操作，建模应用功能是指利用数学知识去解决实际生活情境中的问题．

3.2 数学表征功能性框架

表1即表征功能性框架，包括三级指标：第一级指标是按照表征的功能进行分类，包括表达交流，操作转换和建模应用；第二指标是对表征功能内涵的描述：表达交流包括符号表达和图形图表，操作转换指思维操作和模型操作，建模应用即情境应用；第三级指标是根据文本《20世纪中国中小学课程标准·教学大纲汇编（数学卷）》和21世纪以来的课程标准的内容以及第二指标进行更为具体的分类，符号表达包括书面符号、口语表达，图形图表包括图形、图表的认识或绘制，思维操作包括计算（度量）以及逻辑推理，模型操作包括实物模型（算盘）、计算器的使用以及计算机的模拟，情境应用包括情境问题的解决和对数学知识的实际应用．

表1 数学表征功能性框架

3.3 编码流程

表征功能编码框架制定及编码流程如图1所示．

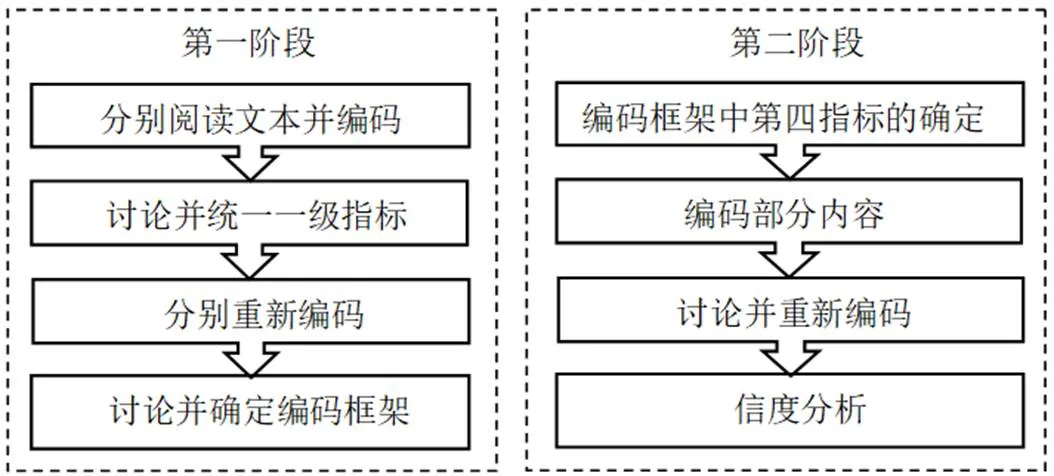
图1 表征功能编码框架制定及编码流程

图1（左）是表征功能编码框架制定的流程图，首先3人分别阅读文本并各自编码，在进行多次讨论之后统一一级指标，之后根据确定的一级指标分别重新编码，再在多次讨论后确定编码．图1（右）是各个学段的数学表征功能编码的流程图，首先确定编码框架中第四指标，再编码文件的部分内容，并且在多次讨论后重新编码，最后随机选取部分年份编码并进行信度分析．其中第四指标是根据第三指标对《20世纪中国中小学课程标准·教学大纲汇编（数学卷）》的内容提取的关键词，并且因年级、知识内容的不同而不同．编码所得数据即第四指标关键词在文本中所提次数．在编码过程中，为了充分展现各个年份中的数学表征，遵循以下原则：若某年份的大纲有多个方案则遵循方案一；若某年份大纲中包括五年制和六年制则遵循六年制；若某年份大纲有文科理科之分则遵循理科，若有高低两种标准的大纲则遵循高标准．并且编码的最小单位为短句，以逗号为标准；编码标准参照表中的词若含有两个含义，则编码两次，但是不超过两次．

3.4 编码信度

编码的最后一步是对小学、初中及高中分别进行差异性检验来判断编码是否有效．首先分别对各学段随机抽取6个年份重新编码，再将所得的数据与原来编码中所对应的数据利用SPSS进行成对样本检验，其中小学、初中、高中的相关性系数如表2所示．

由表2可得，3个学段中随机抽取的编码与原编码的相关性系数都较高，且显著性水平均小于0.05，故两次编码数据显著相关，而且其检验值的显著性水平均大于0.05，故认为前后两次编码不存在差异．因此，编码数据是可以信赖的．

4 研究结果及分析

4.1 小学和初中数学表征变化及分析

图2、图3所示，小学算术和初中代数的表征折线图呈现非常相似的趋势．整体上看，小学阶段的表达交流功能伴随建模应用的变化而变化，到初中阶段后则趋于伴随操作转换的变化，说明学生表达交流能力的训练在小学阶段更多地依赖于实际应用，而到初中后则依赖于思维操作和模型操作．从时间维度上大致可以分为3个阶段：1923年之前，注重德育到杜威实用主义的引入，表征功能几乎保持不变；1923—1978年之间，引进国外教育理念，到学习苏联，再到注重双基，有两次较为剧烈的波动，尤其体现在操作转换功能方面；1978年以后，中国特色的基础教育改革稳步推进，表征功能慢慢趋向于稳定．

表2 表征功能编码的成对样本t检验统计

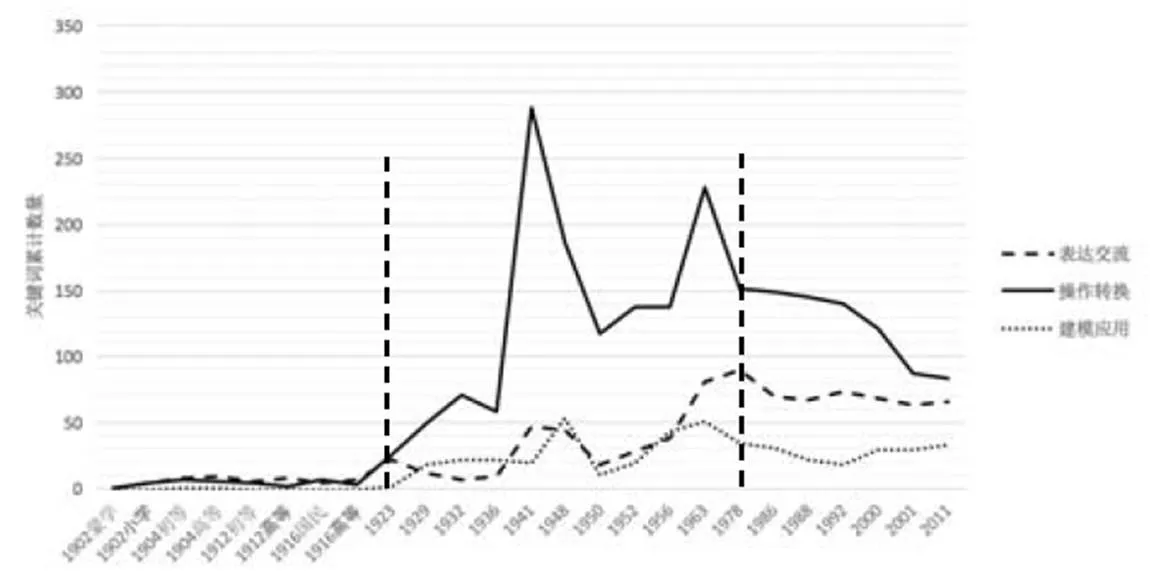
图2 小学数学算术表征功能

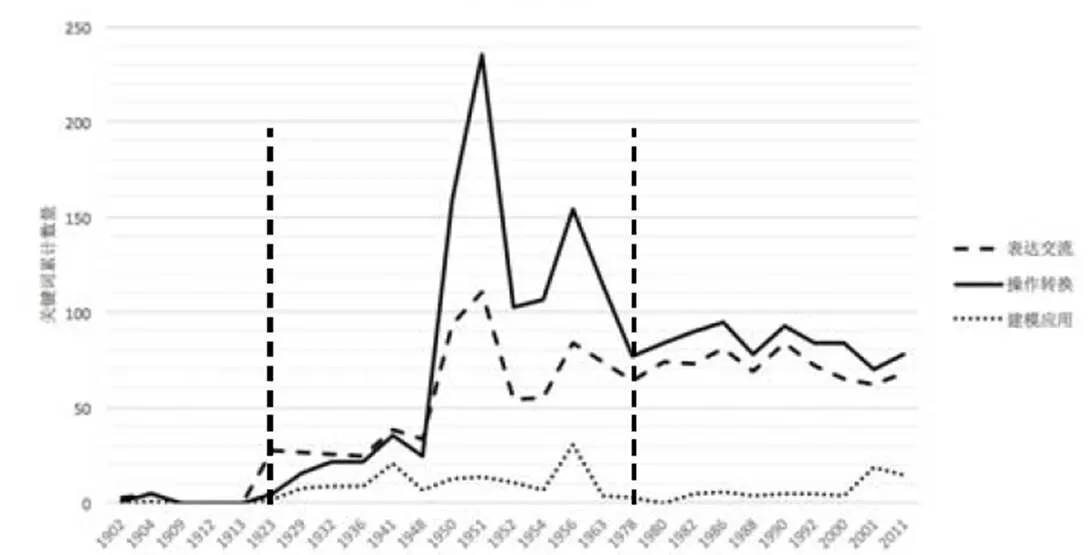
图3 初中数学代数表征功能

（1）第一阶段（1923年之前）．

1923年之前分为两个时期，辛亥革命之前的清朝以及1912年之后建立的中华民国时期．前一时期只颁布了《壬寅学制》和《癸卯学制》，涉及内容极少．而在第二时期的1912年初，教育部成立，并以“注意道德教育，以实利教育、军国民教育辅之，更以美感教育完成其道德”为教育宗旨[25]．在1914—1918年第一次世界大战时期，帝国主义暂时放松了对中国的经济侵略，以及1919年爆发的“五四”运动，促使国内出现了前所未有的教育改革运动，使得全国的教育有所发展[25]．在此期间，美国大教育家杜威（J. Dewey, 1859—1952）的教育思想通过蔡元培、黄炎培的介绍传入中国，陶行知、郑晓沧、胡适等中国学者对杜威的学说做了大量宣传．且杜威于1919年来华后，在中国各地作巡回讲学，将其实用主义教育理论在中国的传播推向了高潮[26–27]，比如1922年公布的《壬戌学制》的指导思想就是杜威的实用主义，该学制即以美国学制为蓝本的现代学制，也称为六三三学制．所以1923年之前，虽然数学表征的3种功能均未体现变化，但为后一时期的变化做了铺垫．

（2）第二阶段（1923—1978）．

这一时期的小学和初中都以1952年为临界点，前后分别有较大波动，将这段时期分为两个阶段，第一时期（1923—1952年）引进国外各种不同的教学学说以及20世纪初国际数学教育改革的进展信息；第二时期（1952—1978年）从1952年开始全面、系统地学习苏联，提出“学习苏联先进经验，先照搬过来，然后再中国化”[28]，后在1963年大纲中强调基础知识和基本技能的重要性．

第一时期（1923—1952）伊始，1923年的大纲在《学校系统改革令》的基础上制定[29]，数学表征的表达交流、操作转换以及建模应用功能都开始被重视．而1936年修订的课程标准公布一年后抗战就开始，中国教育为适应抗战建国的需要对内容进行调整．文件《抗战建国中各科的作业要项的设计》中表明要删除与学生生活无关的问题，以国防上的实用为主，采用国防上的数字及军事上的计算为习题资料，例如应用问题中“工程问题”改为“掘壕问题”“舰力问题”等[25]．所以当时3种功能均受到重视，只是操作转换功能更为显著．而又可能因为当时所需知识水平较低，故1941年大纲中小学的操作转换功能大幅度上升，而初中只是轻微上升．1949年后，开始全面学习苏联，以苏联十年制学校的教学大纲为蓝本[30]，实行凯洛夫的“知识中心”“课堂中心”“教师中心”教学系统．而教育部成立之后，调查学生负担过重的原因之一是数理化三科教材内容多且编排不合理[31]．于是教育部开展座谈会，得出以下原则：精简的目的在于要求教学切实有效，而不是降低学生程度；数学教材尽可能与实际结合，首先要与理化两科的学习结合，又要与经济建设需要的科学知识相结合等[31]．所以当时小学、初中阶段“52大纲”中表征的3个功能都降低了要求，并且首次提到关注基础知识和技能训练，强调数学内容的系统性和逻辑性[28]．

第二时期（1952—1978）在经历“大跃进”之后，中央发布了“关于教育工作的指示”，在全国范围内引起了教育改革运动，重点是学制和教学内容．由于课程内容改革力度过大，导致学生较重的学习负担和教育质量的下降[32]．当时提出“半工（农）半读”，并且政治教育和生产劳动教育被提到突出位置，比如课程计划中包括“工农业基础知识”，所以操作性要求都有所提高．1962年教育部发出《关于1962—1963年度中小学教学用书的通知》，将“初中算术”全部下放到小学[31]，而且人民教育出版社编写1963年中小学数学教材就把“力求避免片面强调联系实际而削弱基础知识，注意基础知识的充实和基本训练的加强”作为编写的指导思想[13]．因此所有算术都在小学完成，又更加注重基础知识和基本技能，故在“63大纲”中，表征的操作转换、表达交流和建模应用功能均有所提高，而初中阶段就有所下降．但在1966—1976年期间，没有统一的数学教学大纲，各省市等自拟编写纲要编写教材[30]，忽视双基，导致全国教学质量大幅度下降[13]．

（3）第三阶段（1978年之后）．

1976年之后，全国进入了全面整顿时期，总结国内外数学教材改革的经验教训，比如20世纪70年代美国在“新数学”运动失败后又主张“回到基础”[27]，于是中国“78大纲”在“63大纲”的基础上进行内容的更新，强调加强双基．1985年教育部总结初中教育指出学生负担较重，所以在“88大纲”中各表征功能有所下降．到21世纪，“01标准”强调“自主、合作、探索、创新”，内容上新增设了“实践与综合”领域[28]，注重创设数学学习的情境，但并未强调数学双基教学，淡化了对基础知识和基本技能的重视[27]，所以当时建模应用功能有所上升，而操作转换功能有所下降．后对“01标准”实施状况调查发现新的教学方式使学生的两极分化现象出现在小学低年级等，故修订后的“11标准”回归“双基”并延伸，明确提出“四基”：义务教育阶段的数学学习，使学生能获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想和基本活动经验[28]．所以这里操作转换功能又有所回升，而建模应用功能有所下降．不过总体上3种功能慢慢趋于平衡．

4.2 高中数学表征变化及分析

高中数学代数表征功能如图4所示．历年高考录取人数如图5所示．

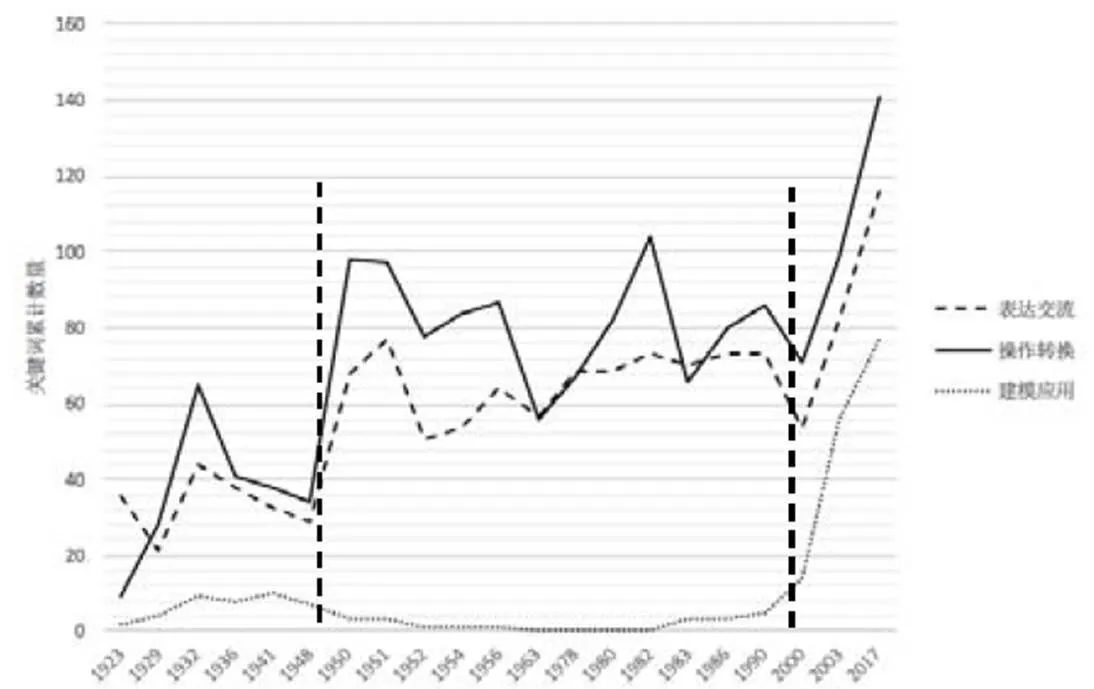
图4 高中数学代数表征功能

图5 历年高考录取人数

高中数学表征的建模应用功能的折线图与高考录取人数折线图十分相似，呈上升趋势，而且表达交流功能伴随着操作转换的变化而变化，总体上也呈上升趋势．时间维度上分为两个阶段：第一阶段（1999年之前）操作转换和表达交流功能波动非常大，并以1963年为平衡点上下浮动，而“63大纲”是多数数学教育家公认的比较完善的大纲；应用功能在这个阶段基本没有受到重视．这一阶段的1949年前，各地高中数学教材混乱，程度参差不齐，故从1949年后开始讨论．第二阶段（1999年之后），高中数学表征的3个功能都迅速上升，尤其在建模应用层面持续受到重视．

（1）第一阶段（1999年之前）．

第一阶段前期（1949—1978），也就是新中国成立初期，高中继续沿袭高校联合招生、委托招生的办法，1950年和1951年各大区高等学校采取联考联招，到1952年，全国普通高等学校开始采用统一考试招生的办法，直到1965年皆实行全国统一招生考试，这段时间高中招生工作是由省市等和高等学校分别处理，并且特别强调政治挂帅和政治路线，对文化水平方面并不重视．而且在20世纪50年代中叶，由美国发起的数学教育现代化运动，直至面向21世纪的教育改革，其中心是数学课程的改革[33]．在这样的背景之下，表征的3个功能均上下浮动很大．1966年《人民日报》发表社论指责高等学校招生考试办法“基本上没有跳出资产阶级考试制度的框框，不利于更多地吸收农民兵革命青年进入高等学校，这种考试制度必须改革”．当时不仅取消了高考，而且也导致了大学停止招生达4年之久．1970年开始，高校开始招收“工农兵学员”．1971年的《全国教育工作纪要》指出：“大专院校招生的主要对象是具有二~三年以上实践经验的优秀的工农兵，一般应有相当于初中以上文化．”1977年恢复高校招生考试制度，文件《关于1977年高等学校招生工作的意见》规定：“废除推荐制度，在政审合格的前提下，采取文化考试、择优录取的方法招收大学新生．”[34]所以在1963之后，直到1978年才出高中新课标．

第一阶段后期（1978—1999），教育部针对数学课程内容与要求太低的状况以及国家建设4个现代化的需要，提出数学课程内容现代化的问题，对数学课程的内容、选择性、编排方式等进行了探索和实践[28]．于是在“78大纲”中增加了许多现代化的数学课程内容，导致数学课程内容太难，与当时学生的基础和师资不相符合．之后的十几年，就围绕“78大纲”进行减少内容、降低难度的调整．但由于高等教育资源严重匮乏，升学率成为社会乃至部分教育主管部门评价中学教育的关键指标．为了克服片面追求升学率和越来越严重的应试教育倾向，1980年中期又对高考终生制度进行试验和改革，比如：定向招生、委托代培招生，推荐考试等．1990年初，人们越来越多使用“应试教育”来概括高考制度下的基础教育，“素质教育”概念也逐渐流行[34]．所以虽然表征的表达交流功能和操作转换功能波动大，但建模应用功能慢慢得以重视．

（2）第二阶段（1999年之后）．

这一时期，表征的表达交流、操作转换以及建模应用功能都迅速上升，开始重视数学知识与实际问题的联系，也为适应时代发展对人才素质提出的新要求．高中教育课程是义务教育阶段后普通高级中学的主要课程，是为学生的可持续发展和终身学习创造条件．1999年教育部出台《面向21世纪教育振兴行动计划》，基于解决经济和就业问题，扩大普通高校本专科院校招收人数，高校开始趋向“大众教育”，从图5也可以看出高考录取人数在20世纪开始逐年递增．但是对于高校优势教育资源的竞争激烈程度有增无减．多年来所批判的应试教育倾向，高考是主要诱因，升学压力下，教师的题海战术导致学生的学业负担增加也成为一个问题．高考制度的择优原则本身就赋予它竞争的属性，这也是中国基础教育多年来陷入片面追求升学率的泥沼而无法自拔的原因．高考作为主导基础教育的中心，数学课程标准作为指导教材编制、教学实施、以及教学评价的唯一标准，如何发挥高考维护社会公平、选拔高等学校合格新生的同时，减少它对中学教育的负面影响成为人们关心的重要问题．03版和17版数学课程标准都要求把数学探究和数学建模渗透在数学课程中，这应该是导致3个功能大幅度提高的重要原因．其中17版从数学素养的角度评价分析学生成就，并且将课程分为必修、选择性必修和选修课程，区分了不同程度学生的要求，对于共同要求和选择性有了一定的平衡．但因为对数学实践情境、数学探究活动及数学建模的强调，又导致了数学表征以及表征之间相互转换方面要求的提高，所以如何平衡时代发展产生的新知识与核心知识尤为重要．

5 讨论与结论及启示

针对文本《20世纪中国中小学课程标准·教学大纲汇编（数学卷）》从数学表征的功能角度进行编码分析，并寻找文献及史料作为依据来解释数据．结果表明数学表征的功能随课程标准的变化而变化，并且3种表征的侧重点和相互关联性在不同学段有不同特点．具体而言，小学阶段的学生在表征的表达交流方面主要是通过情境问题和实际应用来培养的，而初高中学生的表达交流能力则是通过较为抽象的思维操作和模型操作来培养的；操作转换在3个学段均起到主导作用；至于数学表征的建模应用功能，在小学、初中阶段并没有受到足够重视，在高中阶段新课程改革后才逐步受到重视．所以学生的教学应该随学段的不同而在表征方面有不同的侧重点，而且需要重视数学建模功能在培养学生数学素养的重要性．当然，由于各表征功能在不同时期会因时代的变化而有不同的需求，于是把握新知识与核心知识之间的平衡显得非常重要．

研究尚存一些不足之处：首先表征在语义学、心理学等不同领域有不同的内涵，这里仅从教育领域的视角出发分析表征的功能性指标；其次，研究涉及的历史材料主要围绕课程标准，而没有对教科书进行比较分析．因此结论具有一定的局限性．

[1] 喻平．知识表征与数学学习[J]．上海师范大学学报（哲学社会科学·教育版），2002（1）：49–52．

[2] CAI J, LESTER J R. Solution representations and pedagogical representations in Chinese and U.S. classrooms [J]. Journal of Mathematical Behavior, 2005, 24 (3): 221–237.

[3] 胡典顺．美国学校数学教育中的“表征”及其启示[J]．数学教育学报，2009，18（5）：72–74．

[4] NCTM．美国学校数学教育的原则和标准[M]．北京：人民教育出版社，2000：66．

[5] NISS M. Mathematical competencies and the learning of mathematics: The DanishKOM project[C] // GAGATSIS, ATHANASIOS. 3rd mediterranean conference on mathematical education: Mathematics in the modern world, mathematics and didactics, mathematics and life, mathematics and society. Athens: Hellenic Mathematical Society; Cyprus: Cyprus Mathematical Society, 2003: 115–124.

[6] OECD. Measuring student knowledge and skills: The PISA 2000 assessment of reading, mathematical and scientific literacy [M]. Paris: OECD Publishing, 2000: 51.

[7] OECD. The PISA 2003 assessment framework: Mathematics, reading, science and problem solving knowledge and skills [M]. Paris: OECD Publishing, 2004: 41.

[8] OECD. PISA 2009 assessment framework: Key competencies in reading, mathematics and science [M]. Paris: OCED Publishing, 2010: 110.

[9] OECD. PISA 2012 assessment and analytical framework: Mathematics, reading, science, problem solving and financial literacy [M]. Paris: OECD Publishing, 2013: 32.

[10] OECD. PISA 2015 assessment and analytical framework: Science, reading, mathematic, financial literacy and collaborative problem solving [M]. Revised Edition ed. Paris: OECD Publishing, 2017: 71.

[11]  NCTM. Principles to actions: Ensuring mathematical success for all [M]. Reston: NCTM, 2014: 24.

[12] 梅瑞迪斯·高尔，乔伊斯·高尔，沃尔特·博格．教育研究方法[M]．6版．北京：北京大学出版社，2016：400．

[13] 张奠宙．中国数学双基教学[M]．上海：上海教育出版社，2006：2，5，8．

[14]  GALL M, GALL J, BORG W. Applying educational research [M]. 6th ed. Boston: Pearson Education, Inc, 2010: 466.

[15]  BRACHMAN R J, LEVESQUE H J. Knowledge representation and reasoning [M]. San Francisco: Elsevier, Inc, 2004: 3.

[16] 张晋宇，姜慧慧，谢海燕．数学表征与变换能力的评价指标体系研究综述[J]．全球教育展望，2016，45（11）：13–21．

[17] 鲍建生，周超．数学学习的心理基础与过程[M]．上海：上海教育出版社，2009：114．

[18] 喻平．数学教育心理学[M]．南宁：广西教育出版社，2004：56.

[19] 王兄．论数学表征系统[J]．数学教育学报，2008，17（3）：8–10．

[20]  LERMAN S. Encyclopedia of mathematicseducation [M]. Dordrecht: Springer, 2014: 409.

[21] 唐剑岚．国外关于数学学习中多元外在表征的研究述评[J]．数学教育学报，2008，17（1）：30–34．

[22] 李静．哲学视野下小学数学多元表征变式教学构建及其实证研究[J]．数学教育学报，2016，25（5）：45–48.

[23] 徐斌艳．数学学科核心能力研究[J]．全球教育展望，2013，42（6）：67–74．

[24] 曹一鸣，黄秦安，殷丽霞．中国数学教育哲学研究30年[M]．北京：科学出版社，2011：152．

[25] 魏庚人．中国中学数学教育史[M]．北京：人民教育出版社，1987：102，182，328．

[26] 王建磐．中国数学教育：传统与现实[M]．南京：江苏教育出版社，2009：55．

[27] 张奠宙．数学教育纵横[M]．南宁：广西教育出版社，2018：7，14．

[28] 曹一鸣，梁贯成．21世纪的中国数学教育[M]．北京：人民教育出版社，2018：120–121，137，148．

[29] 课程教材研究所．20世纪中国中小学课程标准·教学大纲汇编（数学卷）[M]．北京：人民教育出版社，2001：14．

[30] 吕世虎，吴春燕，陈婷．20世纪以来中国中学数学课程内容综合化的历程及其启示[J]．数学教育学报，2009，18（6）：1–5．

[31] 魏群，张月仙．中国中学数学课程教材演变史料[M]．北京：人民教育出版社，1996：2–3，96．

[32] 刘兴祥，徐志强，赵耀峰．中国数学课程标准发展史[J]．延安大学学报（自然科学版），2006，25（2）：21–25．

[33] 李善良，宁连华，宋晓平．中国数学课程研究30年[M]．北京：科学出版社，2012：115．

[34] 王伦信，曹彦杰，陈绵杰．新中国中学教育改革研究[M]．上海：上海教育出版社，2008：242．

Arithmetic and Algebra Representation Function in Mathematics Curriculum Standards in China since the 20th Century: Its Change and Enlightenment

SHEN Yang1, ZHANG Jin-yu2, 3, LI Na1, BAO Jian-sheng1, 3

(1. School of Mathematical Sciences, East China Normal University, Shanghai 200241, China;2. College of Teacher Education, East China Normal University, Shanghai 200062, China;3. Shanghai Research Base for School Mathematics Education, Shanghai 200241, China)

On the basis of arithmetic and algebra inand the curriculum standards since the 21st century, the variation trend of the arithmetic and algebraic representation in Chinese primary and secondary school mathematics curriculum standards from 1902 to 2017 was investigated using the historical research method and coding-analysis by focusing on three functions of mathematical representation (i.e., expression communication, operational transformation and modelling application. Results showed that, the function of mathematical representation changes as the curriculum standard changes. Moreover, the emphasis and correlation among three representation functions also had different features in different stages. Particularly, the function of expression communication was depended on the modelling application in the primary school stage, but the operational transformation in the middle and high school stage. The function of operational transformation was dominant in three stages. The function of the modelling application was not taken seriously in the primary school and junior high school. However, more attention had been paid to the high school stage since the new curriculum was reformed.

mathematical representation; representation function; arithmetic; algebra

2019–03–16

教育部人文社会科学重点研究基地重大项目——中国学生数学素养测评研究（16JJD880023）；上海高校“立德树人”人文社会科学重点研究基地——华东师范大学数学教育教学研究基地项目（A8）

沈阳（1992—），女，浙江东阳人，博士生，主要从事数学课程与教学论研究．

沈阳，张晋宇，李娜，等．20世纪以来中国数学课程标准中算术与代数表征功能的变化及启示[J]．数学教育学报，2019，28（3）：12-17．

G423.07

A

1004–9894（2019）03–0012–06

[责任编校：周学智、张楠]