基于密度聚类的线段特征提取方法

杨忠炯，王臣臣，周立强，易圣先

（中南大学，长沙 410000）

0 引言

同时定位与建图是近些年来机器人领域研究的热门话题，是实现机器人在未知环境自主导航的关键技术。SLAM技术是指机器人能够在未知环境中，通过自身携带的传感器来获取外界信息和自身位姿，以此建立起环境地图和完成自身定位，并在运动中完成地图与自身位姿的更新。

机器人携带的传感器包括激光传感器，相机，毫米波雷达等，其中激光传感器由于其具有同时精确测量距离和方位角的能力，并且受环境影响较小的特点，被广泛应用于各类机器人导航与定位系统。特征地图因其占用内存小，能够高效，全面地表示环境信息，因而被广泛应用在室内移动机器人定位中。而构造特征地图的首要任务就是环境特征的提取，常见的环境特征通常是指几何环境特征，比如线段、角、圆等。而在实际环境中，最常见的特征之一就是线段特征。由激光传感器扫描环境所得的数据中提取线段特征的算法目前主要有霍夫变换，回归法，增量法，分裂合并法等。文中提出一种基于密度聚类的线段特征提取方法。

1 聚类

聚类是一种应用广泛的数据挖掘技术，很多领域都应用到了聚类算法，包括机器学习，图像处理等。聚类将数据按照其相似程度不一的特性讲其划分为不同的簇，同一簇内数据相似程度高，不同簇内数据相似程度较低。聚类算法得到了广泛的研究，许多学者提出了不同类型的聚类算法，包括原型聚类，密度聚类，层次聚类等。对于从激光传感器获取的数据，可以用距离来表征数据之间的相似性。距离计算可以采用5种方式：欧式距离，马氏距离，夹角余弦距离，二值特征的夹角余弦测度，二值特征的Tanimoto测度。鉴于向量间欧式距离计算简便，且基于欧式距离的分类方法使用效果好，因此文中采用欧式距离聚类方法。

相邻两点xj和xj+1之间的欧式距离为记为disted（xj,xj+1）, 设xj，xj+1的特征向量分别为：

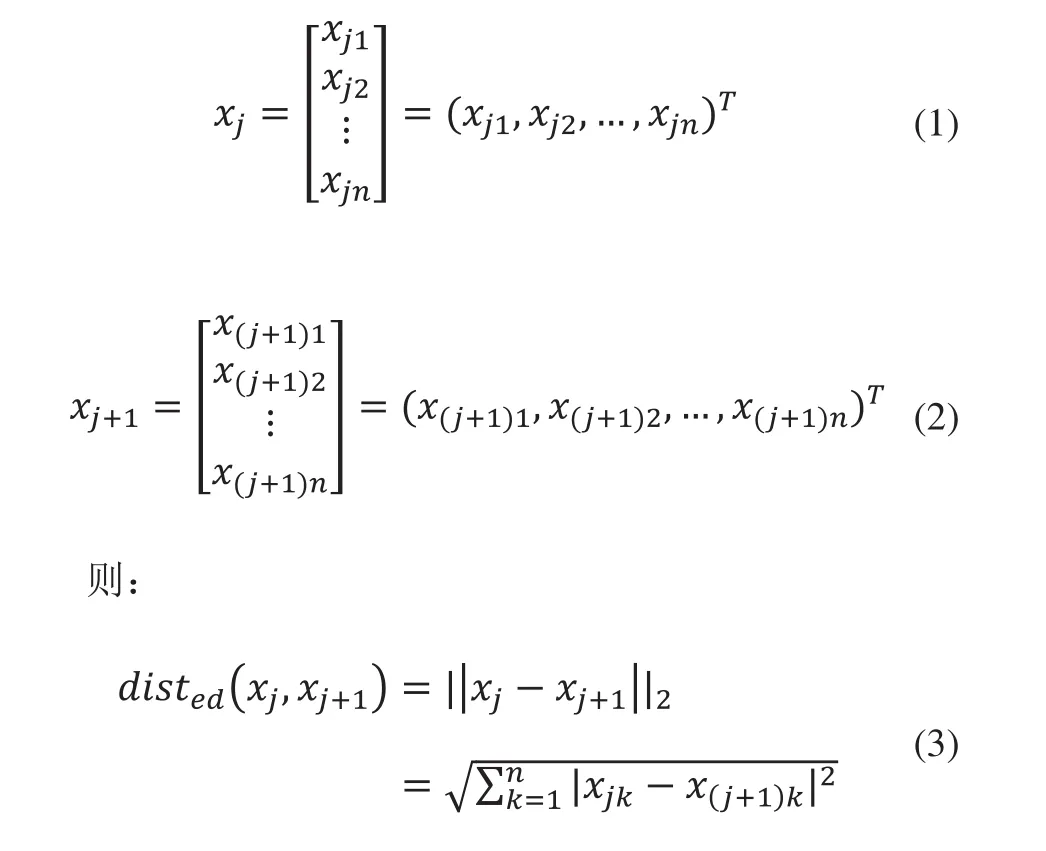
2 基于密度聚类的线段特征提取方法

机器人在室内运动时，遇到线段特征的概率是非常大的，比如桌子，窗户，房梁等，因此对线段特征进行提取就非常有必要。对线段特征进去提取就是要从激光传感器扫描的数据点进行分析，处理，识别出其中的线段特征。

由于激光传感器采集数据是一个实时的过程，所以采集到的数据就不可避免地存在噪声，这些噪声会严重干扰地图的创建，因此在正式的环境特征提取之前，必须对原始数据进行去噪处理，即对数据进行预处理。此外，激光传感器采集的原始数据是完全混合在一起的，为了能够更好地提取环境特征，需要对数据进行区域分割，使其准确地划分为各个路标的数据集。

由此，文中基于激光传感器数据的线段环境特征提取算法由激光传感器数据预处理，基于聚类的区域分割和参数拟合三部分组成。

2.1 数据预处理

在分析激光传感器数据和特征提取的过程中发现，激光传感器数据仍然存在一些不可忽视的问题，这些问题会对特征提取算法的鲁棒性，精度以及时效性带来不良影响，这些问题主要包括：

1）噪声。传感器受其使用环境和自身精度影响都不可避免地会产生噪声，激光传感器也不例外。噪声干扰会导致数据中出现一些孤立的点，但是这并不是真实的观测数据，反而会干扰算法结果，所以预先予以滤除。

2）数据离散化误差。激光传感器数据是高度离散化的，当目标与激光传感器距离较远时，其离散化误差也就越大，因此需要对距离较远的数据滤除，以防干扰算法结果。

为了减小上述因素对特征提取的影响，需要对原始数据进行滤波处理，常用的滤波算法有中值滤波，高斯滤波和均值滤波等算法。文中采用中值滤波方法对激光数据平滑处理。

中值滤波是一种非线段性平滑技术，把数据集中一点的值用其领域内各个点的中值代替，从而减小数据的离散性，使其更加接近真实值。中值滤波算法主要取决于窗口N。

计算公式如下：

式中N表示窗口大小，pmid代表中值，mid是取中值的函数，pi表示原始数据。

算法：中值滤波算法；

输入：激光传感器数据；

输出：去除噪声后的中值数据；

1）选择一个窗口大小N；

2）带入数据p1-pN；

3）把p1-pN排序，并计算出中位数pmid；

4）窗口中数据的中间数替换为pmid；

5）窗口数据前移一位，并重复3），4）步骤；

6）窗口到达右端终点，中值滤波完成。

经过以上的数据处理，能够有效地减小离散化误差，部分偏离线段的数据点向线段集中，所保留下来的数据都尽量接近真实值，为后面的算法顺利实现做出了保障。

2.2 基于密度聚类的区域分割算法

区域分割是根据数据点的位置分布，划分可能属于同一个特征的数据点集。理论上，每个点集对应一个线段特征。SLAM研究的是未知环境，对于环境是没有任何先验知识的，因此对当前数据应该分割成多少个子集是完全不知道的，这恰恰和机器学习中的聚类分析相一致。文中采用基于密度聚类的算法对激光数据进行区域分割。

DBSCAN是一种著名的密度聚类算法，它把具有足够高密度的数据划分为一簇，并能够在噪声的干扰下发现任意形状的簇。DBSCAN基于一组“邻域”参数

来判断数据的紧密程度，对于某数据集D（x1，x2，…，xm），有以下五个定义：

1）邻域：空间内任意一点xi的邻域是以该点为圆心，半径为ρ的圆形区域内的点的集合。记为Nρ（xi）={xj∈D│dist（xi，xj）≤ρ}，dist（xi，xj）表示xi和xj之间的距离。

2）核心对象：若xi的的邻域内至少包含MinPts个样本，则xi是一个核心对象。

3）密度直达：若xj在xi的邻域内，且xi是核心对象，则xj由xi密度直达。

4）密度可达：若存在α1，α2，…，αn，其中α1=xi，αn=xj，且αi+1由αi密度直达，则xj由xi密度可达。

5）密度相连：若xk使得xj和xi均由xk密度可达，则xj和xi密度相连。

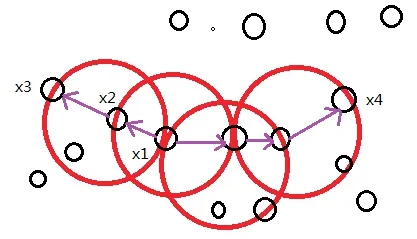
图1 DBSCAN基本概念图

如图1所示，红色线段大圆表示其邻域，x1是核心对象，x2由x1密度直达，x3由x1密度可达，x3与x4密度相连。基于上述定义，DBSCAN将簇定义为：由密度可达关系导出的密度相连样本集合。文中用欧式距离来表征数据点之间的相似性，其DBSCAN算法的具体步骤如下：

1）确定样本邻域ρ，MinPts，设区域分割之前的数据集B（x1，x2，…，xn），

2）从数据集中任意选取一个点x1，判断|Nρ（xi）|≥MinPts是否成立，若成立，则xi为核心对象，加入核心对象集合B中。

3）从集合B中随机选择一个核心对象xj，寻找由它密度可达的所有点，将其加入一个新的集合C1，形成第一个聚类簇，并将C1中包含的核心对象从B中去除。

4）继续访问数据集中的下一个点，重复以上过程，直到处理完数据集中所有的点，得到m个聚类簇Cm。

5）将没有包含在聚类簇中的数据视为噪声干扰，予以删除。

2.3 参数拟合

经过上述对数据的处理后，下面就要对聚类得到的集合ci中的数据点进行线段特征拟合。文中采用最小二乘法进行参数拟合。

图2 线段特征在坐标系下的表示

如图2所示，线段表达为：

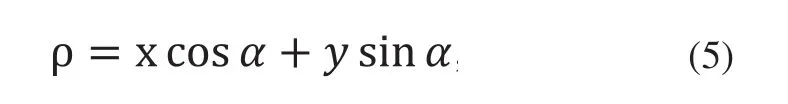
ρ为极点到线段的距离，α为极点和线段的垂线段和x轴的夹角。最小二乘法原理：当所有的点到线段的距离（Δρ）的平方之和最小时，此线段可以被认为是对所有点的最好的线段拟合，即：

上述的（xm，ym）是第m个数据点在坐标系下的坐标，上面的公式分别对α和ρ求偏导等于0得：

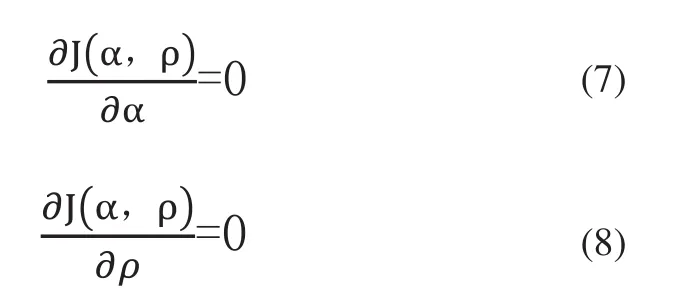
可得线段参数：

综上所述，所求得使式(6)成立的α，ρ代入式(5)，所得即为线段特征。

3 结束语

文中针对基于激光传感器的线段特征提取，引入密度聚类的方法，其基本技术路线图如图3所示。

图3 基本技术路线图

本方法通过引入密度聚类的思想对激光传感器数据进行区域分割，提出了一种新的线段特征提取方法。首先对原始数据进行滤波处理，去除噪声，然后基于密度聚类进行区域分割，并去除不合理特征点，最后采用最小二乘法进行参数拟合，完成线段特征提取。对slam算法中的特征提取的准确性和鲁棒性的提升有借鉴意义。