以量纲分析重新发现普朗克公式
2019-07-08邓崇林
邓崇林
(独立研究员)
1 写在前面
查阅量纲分析针对黑体辐射方面所做的文献,无论国内外的书籍或期刊,大都是直接拿现成的普朗克常数来当系统物理量进行分析。这样布置的话,一来,布置本身就成了为最后的结果而设计的特别安排,以先入为主观念推导出普朗克的黑体辐射公式;二来,习作易倾斜于量纲“计算”,反倒忽略了量纲“分析”过程所夹带对问题的观察和思考;三来,如此布置,彰显不了量纲分析的潜在威力以及盲点,因此,特别需要深入了解其特性,才能取长补短;最后,感受不到其奧妙惊人之处,从而无法深刻体验量纲与物理方程有着紧密关系。因此,这些理由就成了本文的研究动机。
本研究的目标是从经典物理范畴开始探讨黑体辐射规律,并不针对普朗克公式,而且所做的假设都很直观,并不是特别为最后的结果而设计的。量纲分析法[1]是研究物理问题的重要方法之一,但推测物理规律仅仅靠量纲分析是不够的,还要辅予物理基本概念、基本规律、数值分析的推敲,甚至还要运用思想实验,并运用自创的属性拟合手法,过程最大程度依客观条件指导下进行分析与研判,这样一路发展下来,不只能定性还能定量得出量纲分析下Π函数关系式的黑体辐射公式,并找出其特有的物理图像,之后再证得与普朗克公式是等价的。
2 研究对象与方法
回顾黑体辐射物理史,在普朗克发表其黑体辐射公式之前,就有4个辐射公式,按时间进程分别是1879年式(1)的斯特藩-玻尔兹曼定律[2]、1893年式(2)的维恩位移定律[3]、1896年式(3)的维恩分布律[4]、1900年式(4)的瑞利-金斯分布律[4],现条列如下:
为了后续量纲分析的顺利开展,这里要先对上述比较复杂的物理量符号及其量纲进行盘查,首先列出重要物理量的符号及其量纲:[能量E]=ML2T-2,[能量密度(E/体积V)]=[u]=ML-1T-2,又[du=ρνdν],[单色能量密度,或称为谱能量密度]=[ρν]=ML-1T-1=[E]TL-3,[辐射本领R]=[总能密度ε·c/4]=ML-1T-2·LT-1=MT-3,熟悉这些与黑体辐射相关重要物理量的量纲之后,才能开展量纲计算,至于量纲分析,这远比量纲计算来得复杂许多,因分析过程会深入对问题的观察和思考,而且量纲分析往往会产生一些无量纲的未知函数或未知系数,这时就需要借助于其他知识诸如已知特例或实验规律,本研究就是拿前述式(1)至式(4)当作已知的实验规律,用于辅助推导出正确的辐射公式。
本研究另一项特点就是运用自创的属性拟合手法,此法乃从结构上采用一种虽不严谨却十分客观的方式,由剖析结构个别属性及其作用切入,从而分进合击拟合出描述问题规律的一种方法,例如黑体辐射这方面问题,19世纪物理学家在这一问题研究上往往得到莫衷一是的解读,其中有对的也有错的,而且错又不全错,在某些范围它又对了,结果同一个问题分别出现式(1)乃至式(4)等4种不同面貌,就像瞎子摸象,结果大象是什么就有了四说:大耳朵、长鼻子、巨躯体、四肢粗,这些答案都不对但也没全错,其实只要了解四肢动物身体的结构属性,很容易就总结出大象的外貌。虽然同一问题从不同侧面得到相异解读,经量纲分析与结构属性相结合,就能加大概率猜出其规律,并加以实验验证、数值分析或其他边界条件,之后就能定量给出正确的物理规律。
由于在经典物理范畴无法有效进行量纲分析,于是考量能量量纲在时空作用下诱导出一个扩充基本量,并假设其为物理基本常数以及假定其量纲为[能量][时间]等二项特征,然后以Π定理求出Π函数关系式,接着运用自创的属性拟合手法,定出Π函数关系式中3处属性并加以拟合,这需依靠已知4个辐射方程加以验证,又由于黑体辐射算是个复杂的系统,分析过程中总是会碰到这样那样的问题,也会面临该如何选择的关卡,例如:①人为设定7个基本量,依题来调整,怎么才适度?②是否扩增物理新常数,理由是什么,定义又为何?③一体多面应如何下手,考量是什么,切入恰当否?④Π函数式面临多选一,选项是什么,依据又为何?⑤3处属性作用合理否,规律是什么,如何拟合法?以上这5道抉择关卡,将会随着深入分析,物理图像先由粗放轮廓再渐次清晰起来,之后答案自然浮显、问题迎刃而解,从而求得量纲分析下Π函数关系式的黑体辐射公式,这还需通过经验公式鉴定,之后再转换求得普朗克公式。
3 以量纲论证物理基本常数的存在性
1859年德国基尔霍夫已经给出黑体辐射是频率和温度两个变数的函数,而与物体质料无关,所以当温度一定时,我们就可以测量辐射能量与频率的关系。这里先试着对式(4)瑞利-金斯公式进行量纲分析,又为了避免与时间T记号产生混淆,特将惯用温度记号T改记为Θ,权宜之计自当留意。设单色辐射能量密度ρν与玻尔兹曼常数k、温度Θ、频率ν以及光速c有关,现在采用MKSK(米、千克、秒、开尔文)制,由Π原理知道最少要有5个合用的物理量才能找出合理的物理公式,依题设关系式ρv=F(k,Θ,ν,c),其中相关物理量的量纲分别是:[k]=L2MT-2K-1,[ν]=T-1,[Θ]=K,[c]=LT-1,[ρν]=ML-1T-1,代入Π原理可解得ρν=Πν2c-3kΘ,果然得出式(4)瑞利-金斯公式。量纲分析如是进行好像很顺利,可不用普朗克常数就能推得瑞利-金斯公式,这是因为该公式本来就是依经典物理学所推导得出的,这样量纲的经典对应物理学的经典,当然保持很高的一致性。经典物理范畴下的量纲分析,虽然也能算出无量纲量Π,然而这不能解决黑体辐射的问题,因为该方程早就知道是错的,而且频率愈高愈加快发散导致紫色灾难,这凸显了量纲分析本身的工具局限性,它并不能鉴定所得物理方程的正确性,况且式(3)维恩分布公式的单色辐射能量密度也同式(4)一样是与玻尔兹曼常数、温度、频率以及光速有关,为何先前的量纲分析结果并不符合此条式(3)成频率三次方的方程规律;若单单针对式(2)维恩位移定律进行量纲分析,由于波长与频率、光速两者有直接关联,而光速是常数应保留,因此把频率剔除,如此设λ=F(Θ,c,k),但是系统相关物理量的个数n与基本量的个数m都是4个,按Π原理知道两者相减为零的结果,就是无法求出无量纲的量。同样情况也发生在式(1)斯特藩-玻尔兹曼公式的量纲分析上,而且这两条公式都是正确的,却都好像少了一个物理量似的,导致无法进行量纲分析。经典物理理论在量纲分析热辐射时所遇到的困难,并造成以上无奈情况的,就有两种可能,要不就是Π原理靠不住,因为该方法考量的不够全面[5,6],或许需用比较严格的无量纲分析;要不就是物理体系没能提供足够的物理量,使得Π原理无法进行有效分析,因而在经典物理范围需用考量一个额外的未知物理基本常数。这是个很基本且关键的问题,不要急着做判断,总之,需要再深入探讨下去。
现在暂时跳开前述问题的牵绊,我们先回到现象本身深入审视一番。黑体辐射的问题,在于一个黑体在热平衡下,如何将热能分配给不同频率(或波长)的光波发射出去,其核心问题都是围绕在能量上有关,然而在国际单位制中,制定了7个基本量:长度、质量、时间、电流、温度、光强度和物质的量,并没将能量的量当成是基本量,因为能量是个导出量(induced unit),由于制度规范的原故,导致少有人会将能量当成是基本量。Π定理基本上不受这种人为框框条条的限制,以数学角度来看,只要这些量纲互相独立都行,因此这里将扩充一个采用能量量纲[E]的基本量,并用来取代质量量纲[M],这样不只能简化量纲表达式,也容易聚焦于问题本身,同时也回答了①人为设定7个基本量,依题来调整,怎么才适度的问题。
接着从物理角度仔细审视所选的能量、长度、时间、温度等4个量(ELTK)的量纲,它们彼此互相独立,又会相互影响,怎么说呢,例如以做为问题核心的能量来看,在经典物理的范围内黑体辐射的辐射能量密度u的量纲是[能量]在[空间]上的表征,而玻尔兹曼常数k的量纲则是[能量]在[温度]上的表征,唯独[能量]并没有在[时间]上的表征,现在黑体辐射所面临的时空问题,虽然已有[能量] [空间]外在(显)作用的表征,如若进一步思考在时间上发挥[能量]内在(隐)作用的表征,没有道理不存在有一个量纲是[能量] [时间]的物理量,但就经典物理学对黑体辐射体系来讲,根本没有这种物理量,因此,有必要加以定义还潜藏着未知的物理量,由于是内在作用的关系,它潜藏在经典物理的范围里而不被轻易发现,它将如同玻尔兹曼常数只能是个物理基本常数,在黑体辐射现象背后深层地影响着整个体系的表征,于是这里将做两项特征假设:一是系统相关物理量方面现假设存在有一个物理基本常数φ;二是其量纲假设为[能量] [时间],显然,目前有4个量(ELTK)的量纲,即m=4没有变,至于体系所能考量的物理量个数则会多增加一个,如此也回答了②是否扩增物理新常数,理由是什么,定义又为何的问题。
4 用Π定理找出斯特藩公式背后的无量纲量
当普朗克开始研究黑体辐射问题时,首先切入的是维恩分布律与瑞利-金斯分布律这两组公式,并用内插法得到了后来以他的名字命名的普朗克公式[7],由于本研究方法是用量纲分析手法,如今面对4个方程,要选哪一条开始着手,还是说,有样学样,采行同普朗克研究的切入点呢,于是要问③一体多面应如何下手,考量是什么,切入恰当否?其实钱学森已总结出答案,对复杂系统进行纲量分析要从小规模开始抓起[8],黑体辐射算是复杂系统,在前面所列4个辐射公式中,式(1)的斯特藩-玻尔兹曼定律与式(2)的维恩位移定律,它们的数学形式都相对规模较小且简明得多,重点是方程是正确的,这就如同牛顿拿开普勒定律当作自己万有引力理论的试金石一样,这里也需要能检验分析结果的试金石(毕竟自己没做实验来检定,但可以借助于别人的正确试验总结),这样的话,就从历史最久远的方程进行切入分析吧。
现在试着针对式(1)斯特藩-玻尔兹曼定律进行量纲分析,在经典物理的范围内确定黑体辐射能量密度u的主定参量是由光速c、玻耳兹曼常数k和温度Θ等所决定,按Π定理来讲,由于上述的4个物理量n=4,使得n-m=0的窘境下,在经典物理的范围内不可能得出一个无量纲的量,如今在前述已经增加了一个合理假设的物理量φ,现系统有关的物理量的个数n=5,就能靠Π定理求得n-m=1个无量纲的量,于是设u=F(c,k,Θ,φ),采用自订的KJSK (米、焦耳、秒、开尔文)单位制,各物理量的量纲分别是:[u]=EL-3,[c]=LT-1,[k]=EK-1,[Θ]=K,[φ]=ET,代入Π定理的设想,使得量纲关系式为: [u]=(Π1)[c]a[k]b[Θ]c[φ]d,其中Π1是个无量纲量,于是整理列出量纲表如下:
解代数方程组过程如下:
求解之后,根据Π定理可以写出黑体辐射的辐射能量密关系式u=(Π1)c-3k4Θ4φ-3,由于式子中Θ,是为了避免与时间T记号产生混淆而改变的温度记号,现改回常用的温度T记号,于是将辐射能量密关系式改回如下列表示式:
(5)
一般如有阶段性量纲分析结果,之后需要自己(或组里)进行实验来检定,这就启动了小循环的重复检定过程,直到此阶段的经验方程管用为止。这里因可借助前人斯特藩的正确试验总结,反倒可跳过这个过程,也就是,由Π定理算得的方程式(5)指出辐射能量密度正比于温度的四次方是符合实验所得的式(1) 经验规律,后续还会再对全区频谱累积进行量化证明,这样侧面用斯特藩-玻尔兹曼定律检验了本次小规模的量纲分析。又式(1)中的比例系数α是个常数,而式(5)中除了特征物理量φ以外,包括无量纲常数Π1都是常数,因此,特征物理量φ没有理由不是常数,至于是不是物理基本常数,这要到最后才会知晓。现在从式(5)中把Π定理算得的无量纲常数 Π1改写如下:
(6)
以上所得无量纲量的物理意涵虽尚不清楚,但起码与式(1)拉上关系,是个好起头,也顺带回应了③一体多面应如何下手,考量是什么,切入恰当否的问题。
5 建立无量纲量的Π函数关系式
由于黑体辐射公式之式(3)与式(4)都与频率有关,因此设频率ν=F(c,k,Θ,φ),采用自订的KJSK(米、焦耳、秒、开尔文)单位制,并与前一单元的u=F(c,k,Θ,φ)有着4个重复变数,这使得黑体辐射问题拥有6个物理量,而基础量有4个,因此Π定理预计有6-4=2个无量纲的量,其中一个无量纲量已于前一单元求得Π1,现在要求得另一个无量纲的量Π2。设此无量纲量Π2与频率的量纲关系式为: [ν]=(Π2)[c]w[k]x[Θ]y[φ]z,于是整理列出量纲表如下:
解代数方程组过程如下:
求解之后,根据Π定理可以写出频率的量纲关系式
ν=(Π2)c0k1Θ1φ-1
我们将前面式子中的Θ改回常用的温度T记号,重新表成下列式子
(7)
这个物理基本常数φ是热能转光能的桥梁,难怪其量纲是[能量][时间],只要将其乘上时间的倒数也就是光波的频率,自然化作光波所携带的能量。本研究将式(7)视为无量纲量的约化频率,使得光能与热能相除得到一个比值,它表征了每单位热能转换成辐射的转换率,在特定热平衡系统下,它是频率的函数,也就是约化频率会随着不同频率而有不同能量转换率,后续还会沿用这个概念。
按Π定理可以建立Π函数关系式为F(Π1,Π2)=0,也可表成Π1=Φ(Π2),或是Π2=Φ(Π1),至于要如何从中二选一才是正解,由于Π定理并不能告诉我们答案,这要靠自己进一步剖析才行。
首先来看第一个式(6)无量纲量Π1,参考式(5)就知道它是有着正比于黑体辐射系统绝对温度四次方以及与频率无关的特征,它是个总能量级特征项,有了此项才能确保对全域频率积分之后,有着近似于斯特藩经验公式一样与温度四次方成正比的规律表征,但却不能反映辐射能随频率变化的分布,这要靠另一个式(8)无量纲量Π2来达成,该无量纲量有两个任务:一是它本身已探明的内涵,就是反映光能与热能两种能量交换机制之比的能量转换特征项;另一则是以自身为变数所反映的未知函数,它将反映辐射能随频率变化的分布呈中间鼓起且两极限端收敛的双重效应,又由于该函数是以无量纲量Π2为单一自变数,因此对该变数的积分也会是个无量纲的量,所以并不会改变前面总能量级特征项的量纲属性。
经前面的综合量纲分析、总能量级分析和分布特征分析后,发现控制整个黑体辐射现象的,正是这两个特别重要且由Π原理算出来的无量纲量。至此,到底要选哪一种就很明白了,Π1=Φ(Π2)才是能够表征系统的Π函数关系式,但还是不能够放心,因为此前分析总能量级特征项时,只考虑到同式(1)斯特藩-玻尔兹曼定律一样与温度的四次方成正比,忘了还未将其比例系数修正项纳入考量,现在要为之前选定的Π函数关系式补乘上比例常数γ,同时将前面式(6)与式(8)带入并加以调整可得到下列新的Π函数关系式
(8)
其中γ=常数。
上式就是我们找到的Π函数关系式,它是由比例常数项、总能量级特征项和以Π2为自变数的Φ函数项等构成,能够表征系统的辐射能量密度,式中的Φ函数不能再用量纲分析予以确定其函数形式,不过可以确认这是个无量纲的函数。这个Π函数关系式可以采以下的物理直观来理解,就是当黑体处在一特定温度(即T是常数)下达到热平衡,如求其总能量时会对这个Φ函数做Π2变数的积分,其结果也会是无量纲的量,如再上乘比例常数项和总能量级特征项,就成了式(1)斯特藩-玻尔兹曼定律。
其实衡量两个Π函数关系式该如何从中选一,明眼人能很快猜出系统要用哪一个才是正解,因为系统有兴趣的能量密度u就处在式(6)的无量纲量Π1里,已经是显函数可以直接用了,不需要放到Φ函数里将自已变成隐函数,那么简单的一个判断就能完成选用Π函数关系式任务,然而这样做,一来容易忽略掉要纳入比例修正项,二来就失去对Π函数关系式摸底的机会,这会大大地阻碍后续的分析,不可不慎。对无量纲量的Π函数关系式采用了“通过属性定义”而不是用公式定义,这种对所涉及物理量的属性进行分析,从而建立因果关系的方式,可以让人抓住Π函数关系式的主干,这样也回答了④Π函数式面临多选一,选项是什么,依据又为何的问题。
6 从三处属性拟合出Π函数之数学形式
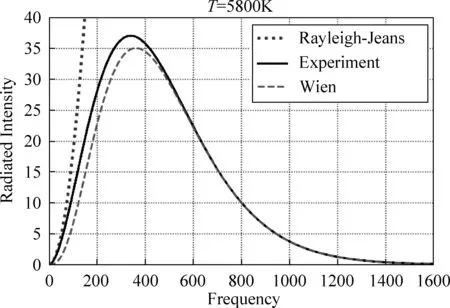
图1 瑞利-金斯分布、维恩分布与实验曲线图
一个物理系统有关的物理量,自有其在该系统中所扮演的属性作用,至于由这些系统相关物理量所组成的无量纲量,同样扮演着特殊的属性作用,有时还构成了系统的重要表征,这一点尤其重要,典型例子就属流体力学的雷诺数,它是重要的无量纲量,它能表征出流体流动的黏性力作用。本节基本上将透过一些分析与研判,来了解式(8)Π关系式中无量纲量的属性作用,再顺势找到其相应的数学形式。我们从图1中可发现式(3)的维恩分布律在高频范围与实验结果吻合,虽在低频部分有较大的偏差,但整个谱线与实验曲线基本蛮符合的[9],维恩公式(3)中的指数函数形式或许应该予以保留,它也是使得能量密度分布曲线有单一极值的关键所在,如此才能满足式(2)的维恩位移定律。又由于指数函数、对数函数、三角函数等超越函数往往是以无量纲量为自变数进行运算[10],如做合理的推测,不得不令人联想到式(8)Π关系式中的Φ函数也应具有指数函数的数学形式,或许只做适度修正,就能逼近实验曲线。另考量式(4)瑞利-金斯分布律会引发紫色灾难[11],因此其数学形式需要大改造,所幸参考图1可发现该公式在低频极限下与实验吻合[4],或许在此极限条件将其改造成带有指数函数的数学形式,使其和式(3)的维恩分布律有着相似的数学形式,就有可能从中猜出Φ函数的数学形式,它的属性作用应该就是主导能量按频率分布画出曲线。这里先回顾指数函数的泰勒展开式如下:
(9)
(10)
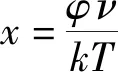
(11)
以上有了三项因子各别的属性,其作用恰好和式(8)Π函数关系式相互对应,因此产生了三处须要进一步确认对应属性作用的数值或数学形式是否正确。
首先要检定第一处常数项γ=8π是否属实,我们将以一个思想实验进行这方面的估算。这里假想设计一个很湊巧的实验,为便于估算及考量电磁波辐射的球对称性,于是制定了一个球体空腔,其半径恰好是某个波长λ,并控制腔壁温度为T,腔内真空,由于腔壁在任何温度下都辐射电磁波,因此腔内就建立了一电磁场,并且腔壁同电磁场将达到平衡,由于此时电磁波在该特定波长λ下的的谐振子振动模数正好是1,现估算该球体空腔内的振动模数密度为[球体积]乘[单位体积元模数密度]乘[电磁波振动为双偏振极性],以下为此运算的计算过程:
又因为黑体辐射与材质及形状无关,所以上述针对特例所估算的属性作用,皆可迳行推广并适用于任何波长,换言之,任何尺寸的空腔皆有此一属性作用,因此,以上估算显示式(11)的常数项其值确认无误,而且它是个无量纲的量,接着按照各别属性作用的对应关系来看,从而也求得了式(8)Π函数关系式中的第一项常数γ=8π。数值求得之后,那该细问此项因数为何是无量纲的量?其属性作用又会是什么?其实答案就在思想实验里,由于前头实验是设计成某个波长λ,并没指定一个值,意思就是可给任意值,所以前述估算结果适用于任意范围的波长λ,而且是无量纲量的常数值,这是热辐射本质呈均方性(isotropic)球对称所赋予的作用,与辐射电磁波相关物理量无关,因而会是个无量纲的常数,这也额外自洽地验证了黑体辐射确实与形状毫无关联。
接下来是第二处式(11)里的特征能量密度项与式(8)Π函数关系式里的中间项,它是由Π1无量纲量并将其中的能量密度变量独立出来而得的,在参考式(6)会更加明白它的量纲同于能量密度,反观式(11)中特征能量密度项的内容,由于在它两旁的项目都是无量纲的量,使得它的量纲会同于单色能量密度,它的量纲并不同于能量密度的量纲,因此我们还是保留原来在式(8)Π函数关系式里的中间项。至于它的属性作用会是什么?目前只以量纲观点进行比较,这不足以进行判断,还看不出端倪。
最后第三处则是式(11)里的约化频率项与式(8)Π函数关系式里的Φ函数项,这里先拿之前式(10)的约化频率项来谈,现考量高、低频两种极限条件下,则前述式(10)的约化频率项会有如下近似结果
(12)
再取式(11)的约化频率项来谈,由于与式(8)Π函数关系式里的Φ函数有着相同自变数的约化频率,于是将两者直接等同之后再考量高、低频两种极限条件下,则会有如下近似结果
(13)
由前述公式(13)在高频范围hν≫kT的极限条件下,过渡到维恩公式,并且在低频范围hν≪kT的极限条件下,过渡到瑞利-金斯公式,这正是图1显示的实验结果,这样就猜出了Φ函数项的数学形式。有了前面三处的估算与拟合结果,就能认定式(8)Π函数关系式如下所示:
(14)
以上初步完成了式(8)Π函数关系式的数学形式,但物理图像尚不清晰,有待进一步探讨。
7 验证斯特藩-玻尔兹曼公式并推算新物理基本常数
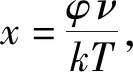
(15)

图2 玻色-爱因斯坦分布函数对约化频率的曲线图
为了进一步了解式(15)函数的特性,我们把约化频率x当横轴座标,以及将该式f(x)函数当纵轴座标,然后运用计算机数值绘图方式产生该函数曲线图如图2所示,式(15)是一个玻色-爱因斯坦分布函数[12],对约化频率所形成的曲线是固定形式的,它并不会随着黑体辐射温度的增减而有所改变,只要是黑体辐射达到热平衡状态,其热能转成电磁波发射的分配情况一律得受此规律所支配。从图2中可观察到式(15)函数支配性地影响着曲线高低走势,又图形是呈上升后下降有单个凹口向下的函数特性,可在曲线上升至下降的转折处让曲线函数对约化频率微分为零,这就意味着曲线函数在此单一峰值处是固定值,该峰值是偏向左方的低频区域,而且从最高峰处越往高频率方向(也就是横轴越向右方)则所分配的成分会快速递减,这表示物体持续加热时当温度愈高则会越难升温,这符合实际的经验判断。由于该曲线是固定形式,这会使得该函数对约化频率的定积分会是个此曲线到横轴所围成的面积,此定积分计算可由文献[13]查得下列结果:
(16)
式(16)定积分是无量纲的量,将其代入式(14)Π函数关系式并对约化频率积分,其计算结果如下:
(17)
物理基本常数分别引用:光速(c)=2.997×108m·s-1,玻尔兹曼常数(k)=1.38×10-23J·K-1,式(1)斯特藩-玻尔兹曼常数a=7.566×10-16J·m-3·K-4,圆周率π=3.14159,代入式(17)可算得
(18)
上述式(17)不只验证了式(1)斯特藩-玻尔兹曼公式,还借助该式求得了式(18)本研究假设的基本常数,很显然它就是普朗克常数,真是一举两得。又由于常用的斯特藩-玻尔兹曼定律是描述一个黑体在单位面积上的辐射功率(即每秒辐射能量),也就是发射本领,因此要将式(17)进行转换[2]如下:
(19)
上式中的比例系数σ称为斯特藩-玻尔兹曼常数或叫斯特藩常量。这样也回应了⑤三处属性作用合理否,规律是什么,如何拟合法的问题。
8 验证维恩位移公式并建构Π函数之物理图像
本节将尝试利用式(17)的微分形式,推算出式(2)维恩位移公式,把这些搞清楚之后,就能建构式(14)Π函数之物理图像。本节将运用前节分析得知玻色-爱因斯坦分布函数对约化频率的曲线是固定形式的特性,且无论黑体辐射的温度是多少,只要达到热平衡状态都受此函数支配,因此,可运用计算机数值分析方式,找出式(15)的最大值,从而得到约化频率为x=2.8214的近似值,再将前节推得的式(18)基本常数值以及玻尔兹曼常数,通通代入式(15)函数中的约化频率,就能到下列公式:
νmax=5.879×1010(Hz·K-1)·T
(20)
以上就是维恩位移定律的频率表达形式,此结果和文献[14]基本吻合,为一定温度下的峰值频率与绝对温度的关系式,又由于还要找出其该定律的波长表达形式,首先找出频率与波长的微分转换因子
(21)
上式负号表示减少频率会导致波长增加,这个负号不影响转换过程,接着由式(17)总能密度取其对频率的微分形式,并借式(21)频率与波长的微分转换因子,可得总能密度对波长的微分形式
(22)
(23)
上述核心函数是以约化波长为单一自变数的函数,如对约化波长进行微分可得
(24)
如果要求极值就是令式(24)该导函数为零,接着排除非零项目之后,只剩下必须为零的项目
(5-x)ex-5=0
(25)
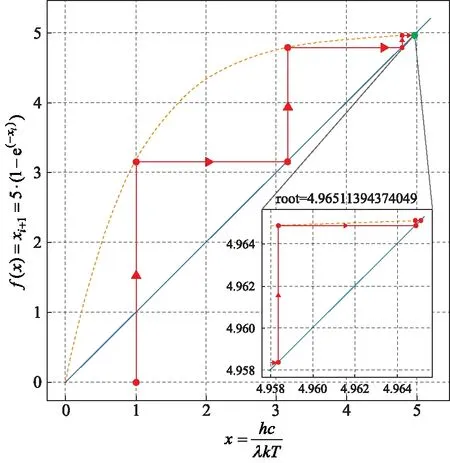
图3 黑体辐射约化波长求根的迭代法过程以箭头线图示
但上述方程并不好处理,这里先用e-x乘上等号两边项目,再移项重新整理可得
x=5-5e-x
(26)
如果对计算机数值分析不陌生的话,就知道上述是个迭代函数x=g(x)=5-5e-x,很显然,零是它的一个根,这里已将其排除,至于另一个根,用一般智能手机里内建的计算器功能就可以求解,首先取一个值为x=3的初始尝试解代入到g(x)=5-5e-x迭代函数里计算,计算器立马算得其值为4.7510646582,再将该值取小数四位为x=4.7511代入到迭代函数中,由于该迭代函数收敛得很快,只要经五次迭代运算,就能得到x=4.9651的近似解,而x=4.9651142317则会是个不动点,此黑体辐射约化波长求根的迭代法全过程类似图3所示。求解固然重要,然而现处在大数据时代,还是具备运用计算机程序求解能力较佳,而且现在有许多免费开放软件可用,其文件丰富自学无碍,例如Python语言,它的scipy程式下的优化模块包含了许多方程求解工具,都是经过优化并且测试过的,因此不要再重新发明轮子,应尽可能地使用现有工具,又为了有别于前述手工迭代计算所用的简单迭代函数,这里改用形式复杂的式(24)微分为零求极值的导函数进行求解,这个导函数若用手工迭代计算是绝对办不到的,这样才能凸显用计算机程序求解的优势,以下就是针对该导函数为零求解的程序代码
1: import scipy.optimize as opt
2: from numpy import exp
3: def dfx(x): return (x**4*((5-x)*exp(x)-5)/(exp(x)-1)**2)
4: print('牛顿法求解之根={:.13f}'.format( opt.newton(dfx,3) ))
上述仅仅用了四行程序代码就能求得根为xmax=4.9651142317443,与文献[15]迭代结果基本一致,再分别引用光速、玻尔兹曼常数以及式(18)本研究假设的基本常数,将这些代入式(21)约化波长定义里,可计算得到下列维恩位移公式:
λmax·T=2.8978×10-3(mK)
(27)
式(27)结果与文献[16]完全一致,这也证明了式(2)维恩位移定律。这里要特别注意,νmax和λmax两者对应的并不是同一个辐射峰值,也就说,它们并不满足频率×波长=光速的关系式,由于当同一黑体处在绝对温度T热平衡时,式(15)约化频率非零根之解,和式(23)约化波长非零根之解,这两者都处在相同的一个绝对温度,此时,绝对温度T就成了转换因子而得到下列关系式:
(28)
式(20)频率与式(27)波长的维恩位移定律两种表达形式在文献[17]中有概略说明,本研究求出峰值频率与峰值波长的式(28)结果与该文献基本一致。
一般文献书籍针对式(2)维恩位移公式的求解过程,是直接将普朗克黑体辐射公式取导数为零求极值的一个直接推论,然而本研究行文至此尚未推导得出普朗克黑体辐射公式,这就必须另辟途径,把前一节结合本节,针对式(15)Φ函数进行数值分析,从而得到本研究经量纲分析所求式(14)Π函数关系式是能够验证式(1)与式(2)两个经验方程,于是式(14)Π函数关系式都通过了在普朗克发表其黑体辐射公式之前所有四条辐射公式的验证,进而确认式(14)就是本研究运用量纲分析得出的黑体辐射公式,又由于经历了前面许多的分析与研读,有了三项有关各别属性作用的了解,综合起来就能为式(14)黑体辐射公式勾勒其物理图像,基本上第一项常数呈现热辐射的均方性(isotropic),使得各个方向的辐射程度都会一样;第二项特征能量密度项只与系统绝对温度有关,是黑体辐射中具有经典热力学系统的重要特征,也就是说,黑体辐射会将带有绝对温度四次方的特征能量密度,均分给每一个约化频率,也可以说是经典热力学能量均分定理(equipartition theorem)的一种推广,在不同绝对温度下,这个量乘上前一项常数,会让图2分布函数曲线往纵轴方向产生不同程度的垂直平移;至于第三项则是反应热平衡下如何给约化频率按特定规律进行能量转换分配,这一项也是无量纲的量,所以,将前述三项连乘起来,这一整体表征了黑体的辐射场具均方性,也推广了经典的能量均分特性,更具有按约化频率进行能量转换分配的特定规律,这是经典热力学所没有的特征,这也是为什么光靠经典理论根本无法处理黑体辐射的原因,因而必须引进新的物理基本常数才能自洽。很显然,这个由式(14)Π函数关系式所表征的黑体辐射公式,其数学形式并不同于熟知的普朗克公式,这会在下节进行等价证明。
9 由Π函数关系式推导出普朗克公式
虽然在第7节里已经证明了本研究假设的式(18)物理基本常数值和普朗克常数是一样的,但这并不表示由量纲分析推得的式(14)黑体辐射公式会同普朗克公式一样,这需要进一步确认。由于在式(1)斯特藩-玻尔兹曼定律都是双方能够确保的条件下,可以安排在黑体同一绝对温度达热平衡时,以其总能量密度进行转换,以下就是式(14)基于这方面的转换计算过程
(29)
于是可从式(29)中分离出谱能量密度如下:
(30)
式(30)与文献[18]里所记载的普朗克谱能量密度的数学形式完全一样,这证明了由式(14)Π函数关系式所表征的黑体辐射公式与普朗克公式是等价的。
10 结语
本次彻底研究黑体辐射问题的经历,充分借鉴了前人个别做了4个不同侧面的半经验方程,并运用量纲分析与辅助手法加以探讨,最后居然能够得出普朗克公式。现总结一下研究心得:
(1) 深入解读钱学森进行纲量分析要从小规模开始抓起[8]的内涵。不单单像本文第4节从小规模方程抓起,而且在量纲的选用上也从小规模开始的。在量纲的选用上,本次研究有两方面考量,一在表征辐射物理量方面,量纲特征如果采[单色能量密度]或[辐射本领]都比[能量密度]来得复杂;二在表征基本量方面,量纲计算采[ELTK]所得的幂次关系式会比[MLTK]来得简洁,况且采用[能量E]当基本量纲能直观反映出黑体辐射现像的核心问题。
(2) 要充分理解运用Π原理分析物理方程的长处与短板。若物理方程的数学形式是由影响问题的物理量具有指数形式且物理量相互间又有乘除关系式的话,那么这类物理方程就是Π原理的天然伙伴,因为用Π原理求得的无量纲量正是这些物理量幂次的乘积的数学形式,最有名的经典例子就是对原子弹的爆炸当量进行的分析估算[19,20],除了这类数学形式之外的物理方程,往往会成为Π原理的天然障碍,例如有着指数函数的普朗克公式,然而却有文献预先为普朗克公式设定ρν=8π(Π1haνbccTd)·[exp(Π2hwνxcykz/T)-1]-1为题目,再令黑体辐射谱能量密度关系式为ρν=F(h,ν,c,T,k),由于有6个变量扣掉4个基本量,于是进行Π原理计算可求得两个无量纲的量,如此这般就轻易得到了普朗克公式,问题是,能这样列题吗?Π原理还没强大到这种地步,它还有不少先天不足之处,譬如在力学进行量纲分析时,长度和速度的方向无法表示等等,这需要引进定向量纲的概念加以改进[20]。遇不足时,就要靠深入剖析问题、实验手段或并用其他方法例如数值分析等等,以期能进一步确定其中的函数形式或系数,另,文献[20]也总结出有关量纲分析一个简单的6步方法以及量纲分析的难点,而且必须通过实践训练才能掌握好这个工具。
(3) 本研究只是以量纲分析湊出普朗克经验公式。1900年10月19日,普朗克提报了依据熵对平均能量取二阶导数在高频和低频的两个极限之间内插而推得到的普朗克公式[21],这是物理史上第一次得到正确的黑体辐射经验公式,虽说与本研究都是凑出来的,然而在问题切入点与所呈现的物理图像却截然不同,然后这些成果皆是缺乏理论诠释的半经验公式,要到1900年12月14日,普朗克报告了自己的研究成果,才为他的经验公式找到了能量量子化的理论诠释。
(4) 本研究成果能降低黑体辐射物理领域的学习门槛。只要具备微积分基础知识,并不对电磁学与热力学有所要求,如此大大降低高中生学习门槛,借由本研究成果,就能更早掌握到有关黑体辐射定性与定量方面的物理知识,在多元角度下促进探索近代物理的兴趣,进而对往后学习有所助益。
