叉车用低压大电流异步电机优化设计
2019-07-05金爱娟唐新雯王居正李乙杨洋
金爱娟,唐新雯,王居正,李乙,杨洋
(上海理工大学光电信息与计算机工程学院,上海200093)
电动叉车是经过电机将电能转化为机械能的装置,电动叉车具有无污染、低噪声等显著优点,传统的电动叉车以直流电机驱动为主。目前,以丰田为首的世界知名叉车生产企业在电动叉车上用交流动力系统替代传统的直流驱动系统,开创了电动叉车技术的新时代[1]。交流动力系统具有多种优势: 对操作命令反应迅速;动力控制准确;零部件安装尺寸小;电机无换向器和电刷,大幅减少了维护保养的工作;容易实现再生制动;更加节约能源,延长了蓄电池的使用时间。
叉车用异步电机不同于工业用380 V高压异步电机,电动叉车采用蓄电池供电,经过逆变器将叉车异步电机的供电电压转换为24 V或48 V,远低于工业用电380 V,母线电压低,使得电动叉车更加安全可靠,因此操作人员触电产生危险的可能性也大幅减少。母线电压低,从而对叉车异步电机的工艺设计要求较高,叉车电机的定子绕组采用多根并绕,定子电阻小。在相同的输出功率下,叉车异步电机的电流比380 V异步电机的电流值大得多,因此应根据需求合理设计电机结构,使电机能够耐大电流,并且自发热较低[2]。同时,叉车通过产生的力矩搬运重物,因此本文采用最大力矩和启动转矩两个参数作为主要的优化目标。
田口法(Taguchi)是日本质量控制专家田口玄一于20世纪50年代初基于正交实验和信噪比技术创立的一套优化设计方法,其基本思想是对产品的制造过程进行稳健性设计,通过控制源头质量来降低生产设计过程中不可控因素的干扰,这些因素包括制造误差、环境湿度、零件间的波动、材料老化等。田口法不仅提倡充分利用廉价元件用于设计和制造高品质的产品,而且提倡使用先进技术来降低设计试验费用,田口法对传统思想的革命性改变,为企业增加效益指出了一个新方向[3]。对比其他局部优化方法,田口法的特点在于可实现多目标优化,并且运用正交实验能在最少实验次数下得出多目标优化设计的最优参数组合,具有实验次数少、考虑因素间相互影响等优点。
本文在提高叉车电机最大转矩、启动转矩的同时,考虑了电机的经济性,提高了电机效率。选取定子槽口宽度、槽口深度、槽深度、转子槽深度、槽上和槽下宽度6个参数作为优化变量,首先利用计算机辅助电磁设计软件ANSYS EM进行参数化扫描,得到单一变量在目标最优的取值范围,进而利用田口正交实验方法进行多目标的优化,并用ANSYS EM软件进行验证。
1 优化变量的确定
本文所有工作均基于1台4极36槽叉车的异步电机,电机相关参数见表1所列,根据ANSYS EM软件建立的电机冲片模型如图1所示。

表1 异步电机基本参数
中国有关中小型异步电机的定转子槽形以及槽极比的标准目前已经十分成熟,常用的电机定子槽形有四种,文中电机选用半闭口梯形槽[4]。定子槽形参数的选取比较复杂,首先要考虑到槽满率,由于槽满率受到工艺水平的限制,因此一定要将槽满率控制在允许范围内;其次还要保证轭部和齿部磁密的适中,齿轭部需要具备很好的机械强度;最后在选择定子槽形深宽参数时,还要考虑对漏抗的影响[5]。
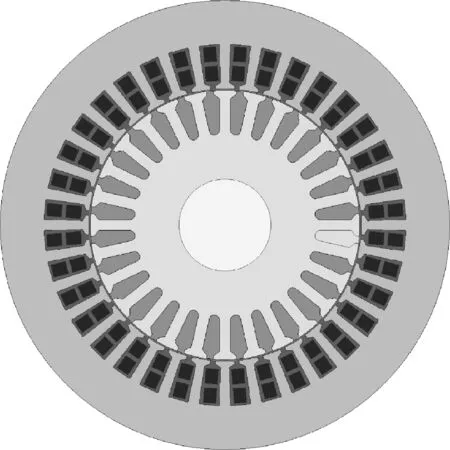
图1 异步电机冲片模型示意
异步电机转子槽相关尺寸的大小对电机的效率、功率因数、最大转矩、起动电流、起动转矩等电机性能指标均有影响,其中起动电流、起动转矩、最大转矩和转差率的影响较为明显[6-7]。关于异步电机定转子槽形相关数据的计算已经相当成熟,鉴于计算过程过于繁琐,本文不再呈现,本文研究的定转子槽形以及选取的优化变量如图2所示。
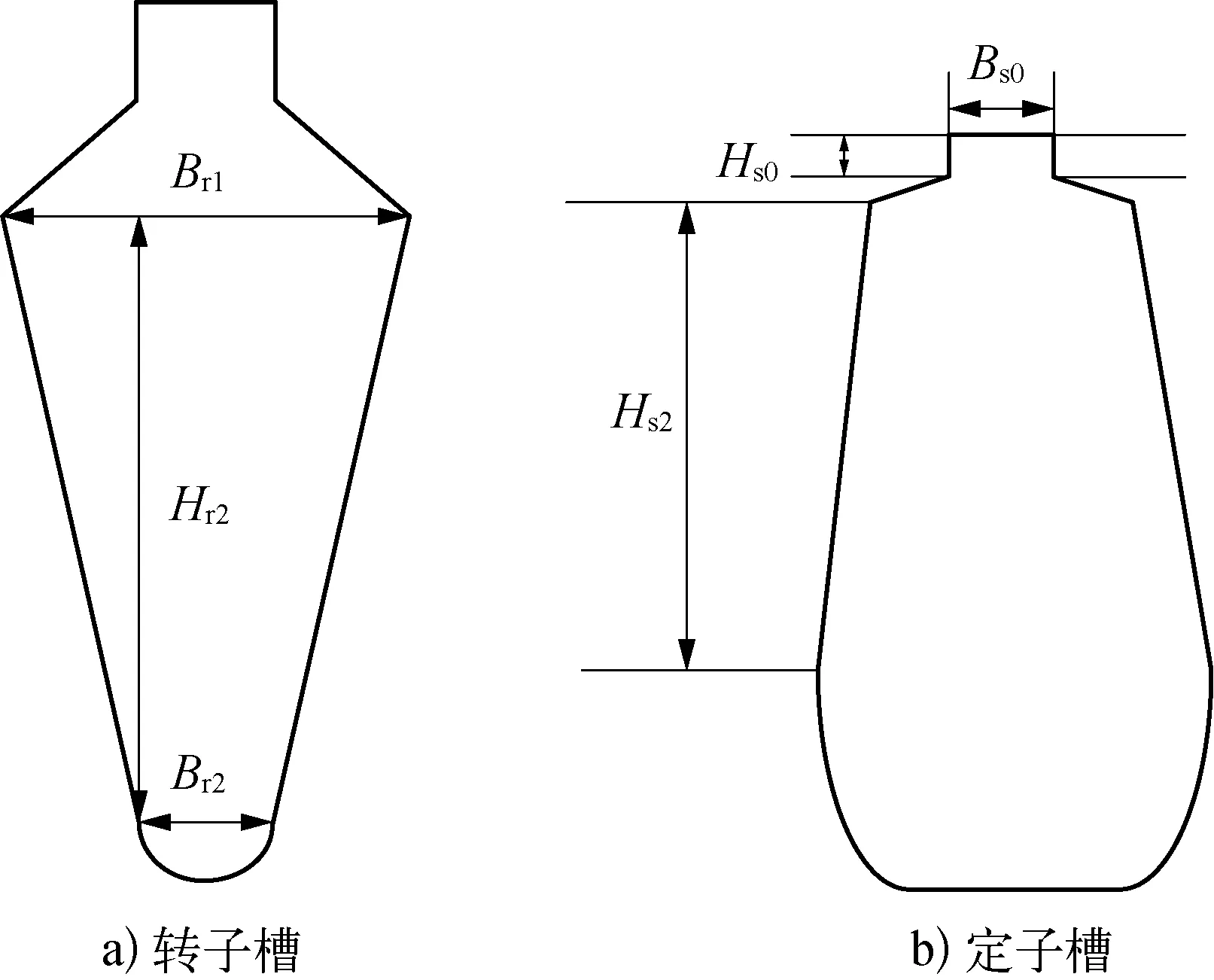
图2 定转子槽形相关优化变量示意
转子槽选取深度Hr2,槽上宽度Br1,槽下宽度Br2作为转子优化变量,定子槽则选取槽口宽度Bs0,槽口深度Hs0,槽深度Hs2作为优化变量。ANSYS EM软件的参数化建模可以快速选取合适的设计参数[8],首先用软件的参数化建模功能分析某个优化变量的变化范围,例如选取Bs0作为优化变量,取值范围为1~2 mm,利用ANSYS EM的参数化建模得到单一优化变量Bs0对相关优化目标的影响曲线,最终确定用于田口实验的Bs0各个水平值,用同样方法得到其他优化参数的各水平值[9]。经过ANSYS EM软件仿真验证的各优化变量的取值范围见表2所列,为了便于分析,分别用字母A~F表示各个优化变量,各个变量的水平值见表3所列。

表2 ANSYS EM仿真验证的各优化变量 mm

表3 各个优化变量的水平值 mm
表3中共有6个变量,总共有56=15 625种组合方案,即使目前计算机技术高度发达,完成如此巨大的工作量也需要耗费大量时间。ANSYS EM软件的电磁模块虽然可支持几千种方案同时进行,但是耗费时间巨大,同时对计算机的性能要求极高,采用田口实验方法只需进行L25(56)=25次实验,较大程度地降低了实验难度与工作量[10]。
2 基于田口法的异步电机优化设计
田口法是一种局部优化设计方法,而全局优化算法如PSO、模拟退火算法等需要建立复杂的目标函数与约束条件。田口法电机多目标优化的流程如图3所示。

图3 田口法电机多目标优化流程示意
田口法与全局优化算法的区别在于田口法通过建立正交表,能在最少的实验次数内搜索出多目标优化设计时的最佳组合,从而完成多目标优化[11]。
利用专业数据分析软件Minitab建立6个变量5个水平值的田口实验矩阵L25(56),通过ANSYS EM软件得到优化目标数据,建立的田口实验矩阵及目标数据见表4所列。

表4 田口实验矩阵及优化目标值
3 实验分析
3.1 平均值分析
为了分析上述6个变量对优化目标最大转矩、启动转矩、电机效率的影响以及各个变量权重,首先对所有结果进行平均值计算,计算如式(1)所示[12]:
(1)
式中:Taverage——某优化目标所有实验数据所得均值;n——实验总次数;Si——第i次田口实验该优化目标所得值。
根据表4中的所有实验结果及式(1)计算得到的3个优化目标的均值见表5所列。

表5 优化目标均值
接下来计算某个优化变量改变时优化目标的均值,即保持某个优化变量的水平值不变,计算相应的目标。例如计算Bs0在水平值为1时对启动转矩的影响,保持Bs0的水平值为1,计算田口实验表中的启动转矩均值,计算如式(2)所示[13]:
(2)
式中:TstA1——保持Bs0的水平值为1时,启动转矩的均值;Test(n)——田口实验编号次数。
同理,根据式(2)可以求得各个优化变量在各水平值下优化目标的均值,见表6所列。

表6 优化变量在各水平值下优化目标的均值
为了更直观地观察优化变量各个水平值对优化目标的影响,根据表6做出的折线图如图4所示。

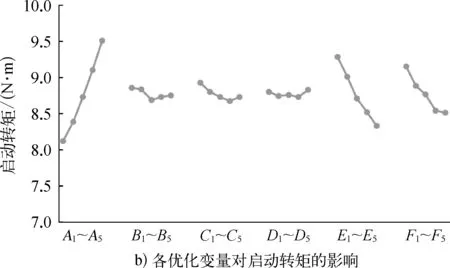
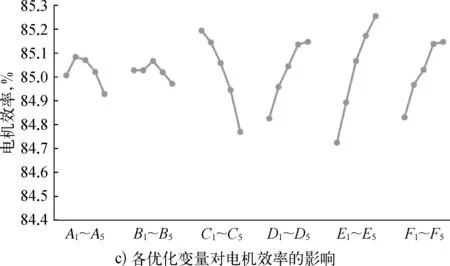
图4 优化变量水平值对优化目标影响曲线
1)从图4a)中可以看出:Bs0(A)与Br1(D)越大,电机的最大转矩越大,其中Bs0(A)的影响极为明显;Hr2(F),Br2(E),Hs0(B),Hs2(C)对最大转矩的影响不明显,使最大转矩最优的各因子组合为A5B1C1D5E1F1。
2)从图4 b)中可以看出:Bs0(A)越大,Br2(E)与Hr2(F)越小,启动转矩越大;Hs0(B),Hs2(C),Br1(D)对启动转矩指标影响不大,使得启动转矩最优的各因子组合为A5B1C1D5E1F1。
3)从图4 c)中可以看出:Hs2(C)越小,Br1(D),Br2(E),Hr2(F)越大,效率越高;Bs0(A)与Hs2(C)对效率的影响指标不大,使得效率最优的各因子组合为A2B3C1D5E5F5。
显然,要使得各个优化目标达到最优,各因子组合并不相同,通过方差分析进而可得到各个因子对优化目标影响所占的比重[15]。
3.2 方差分析
仅进行均值评估并不能直观地反映各个变量对目标值的影响,还要进行方差分析,计算得到数据偏离平均程度的相对大小。通过分析各个参数不同水平下某个性能指标的平均值对于所有实验中该性能指标平均值的方差,可以判断各参数的改变对该性能指标的影响所占的比重,通用的方差计算如式(3)所示:
(3)

根据式(3)以及表4和表6数据求得A~F分别对应的优化目标,即最大转矩、启动转矩、效率的影响比重见表7所列,由于所求的方差数值较小,表7中的数值将其扩大102倍便于表示。

表7 各优化变量5水平值下的方差及所占优化目标的占比值
从平均值分析可知,使最大转矩最优的各因子组合为A5B1C1D5E1F1,使得启动转矩最优的各因子组合为A5B1C1D5E1F1,使得效率最优的各因子组合为A2B3C1D5E5F5。根据表7,因子A对最大转矩及启动转矩的影响比重都为最大,平均值分析指出因子A值越大,启动转矩与最大转矩均越大。因子A对最大转矩的影响比重达到53.2%,即因子A的变化将影响最大转矩值且影响程度较大;其次因子D对最大转矩影响比重大,因子E对启动转矩影响比重大;因子C与E对效率最优影响比重大。因子A与D的选取以最大转矩最优作为标准;B与E的选取以启动转矩最优为标准;C与F的选取以效率最优为标准。结合平均值分析,使得效率最优、启动转矩最优、最大转矩最优的各因子组合为A5B2C1D5E5F5。
根据上述因子水平,利用ANSYS EM软件进行仿真验证,得到的最优因子组合仿真结果与原始设计结果对比见表8所列。

表8 因子优化前后对比
根据表8的优化结果可以看出: 优化前后最大转矩提升了7.2%,启动转矩提升了8.4%,效率提升了0.4%,该次优化在启动转矩及最大转矩方面优化明显,效率优化率较低。缘于影响电机效率的主要因素是电机的长度以及每个槽等效的导体数,该次实验并未涉及,而是通过优化定转子槽型减小损耗间接提高电机效率。
4 结束语
根据电动叉车异步电机性能指标要求,选取了定子槽口宽度、槽口深度、槽深度以及转子槽深度、槽上宽度、槽下宽度6个参数作为优化变量,将最大转矩、启动转矩、效率作为优化目标。利用ANSYS EM软件进行参数化扫描,运用田口正交实验方法设计实验,得到优化结果并用软件进行验证,结果证明了计算机与田口实验相结合优化电机设计的可行性。与传统的电机优化相比,该方法更加方便、快捷。田口法是一种局部优化设计方法,与其他全局优化算法相比,有优点也有不足,如何利用优化算法方便快速地寻找电机设计的最优解有待进一步研究。
