国产某型220T矿用自卸车转向臂受力分析及优化
2019-07-05彭树陈
彭树陈
(中冶京诚(湘潭)矿山装备有限公司,湖南 湘潭 411100)
1 引言
矿用自卸车是在露天矿山为完成岩石土方剥离与矿石运输任务而使用的一种重型自卸车。其工作特点为运距较短,载重大,作业路面恶劣,弯道多。转向机构作为矿用自卸车的重要组成部分,用来控制车辆的行驶方向,由于运行路况复杂多变,使得转向机构所受到的载荷情况也复杂多变,包括负载、各部件间的连接状况及路面传递的冲击载荷等。转向臂做为自卸车转向系统中的重要组成部分,所承受的载荷复杂多变,且冲击强度大,对转向臂的分析显得格外重要[1]。针对国产某型矿用自卸车转向臂使用过程中,存在应力集中的问题,运用有限元分析软件对转向臂应力分析,对应力集中部分进行优化。
2 转向系统简介
国产某型号矿用自卸车采用整体式转向机构如图 1所示,机械结构主要由左右转向臂、转向横拉杆及其他相关附件组成。转向系统为液压动力转向系统,其主要由液压油箱、转向泵、转向油缸、转向集成阀组、流量放大阀、转向阀、转向蓄能器、油管等部件组成。
转向系统的最大压力由流量放大阀块内的转向压力调整溢流阀设定,本系统设定的最大转向压力为18MPa。车辆正常直线行驶时,转向控制装置阀的供油停止,转向油缸内无油压,当轮胎遇到阻碍物并产生较大冲击负荷以迫使车轮偏转,油缸的油口端将出现压力增加,流量放大阀块内部的冲击吸收溢流阀将打开,给油缸泄压,防止更高的压力产生,本系统中冲击吸收溢流阀的设定压力为24MPa。
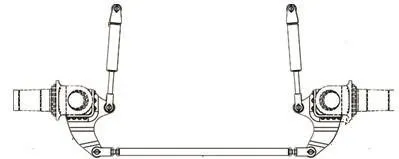
图1 整体式转向机构图
3 转向臂受力分析
3.1 矿用自卸车转向臂受力分析
矿用自卸车转向臂受应力集中导致产生微裂纹如下图2所示。

图2 转向臂裂纹示意图
考虑到矿用自卸车转向臂的工作时受载荷的复杂多变,为简化对转向臂的受力分析,分别按照以下两种典型的工况对转向臂进行力学分析[2-6]:
(1)自卸车满载时静止原地转向,受到来自地面的转向阻力矩。
(2)自卸车发生侧滑,受到侧向冲击载荷。
以上的两种转向工况中转向臂处于静止的临界状态,所以可以认为转向臂是静止,所以可以对转向臂进行静力学分析。为了简化计算,提高分析效率,对转向机构进行一些假设,如下:
(1)不考虑主销内倾角和后倾角以及车轮外倾角、前轮前束对转向臂的影响。
(2)忽略转向系统各个拉杆之间的夹角、间隙和变形。
根据该型号矿用自卸车的参数,在计算中所使用的各个参数如表1 所示。

表 1 计算使用的基本参数
3.2 转向臂受力计算
3.2.1 满载静止转向阻力矩的计算
车辆满载静止转向时,转向臂主要承受转向油缸推力,推力大小可根据转向阻力矩计算公式计算。车轮的转向力矩与车辆的负荷、前轮定位参数和道路表面的摩擦系数、轮胎的参数等有关,并且随着车速的增大而减小。通常情况下,计算的载荷以车辆在静止状态下的原地转向阻力矩为标准。因为在转向时的最大力矩出现在原地转向时候。在转向时转向轮在原地转向时需要克服的阻力,主要包括转向轮绕主销转动的阻力、转向轮与地面之间的静摩擦阻力以及转向系中的内摩擦阻力等。由于轮胎与地面接触十分复杂,精确地计算所有的力是十分困难的。根据原地转向的试验结果,常用的转向阻力矩有三种经验计算公式,分别是:
塔布莱克推荐公式是比较通用的计算公式,本文也将使用这种方法对转向阻力矩进行计算。塔布莱克推荐公式如下:

式中:M 为转向阻力矩 N.m;G 1 为转向桥的负荷,查阅矿车参数可知,满载时前桥负荷为总重的33%,设计重量为载重220t,自重167t,满载总质量为387 t;ξ为有效摩擦系数,其值可由 ξ=e/b 曲线获得,e 为从轮胎与地面的接触中心到转向主销与地面交点间的距离,本系统中e=915mm;b 为轮胎宽度; k 为轮胎与地面接触面积的转动惯性力矩,k2=b2/8。由已知条件代入公式,可得M=103914N.m。
转向推力:

其中:r为转向阻力臂,取r=0.65m。
代入上式计算得 F =1.6e5N。
根据转向结构参数可得到转向动力缸推力与转向油缸伸缩量关系图,如下图3所示,轮胎处于中位时油缸伸缩量为零。
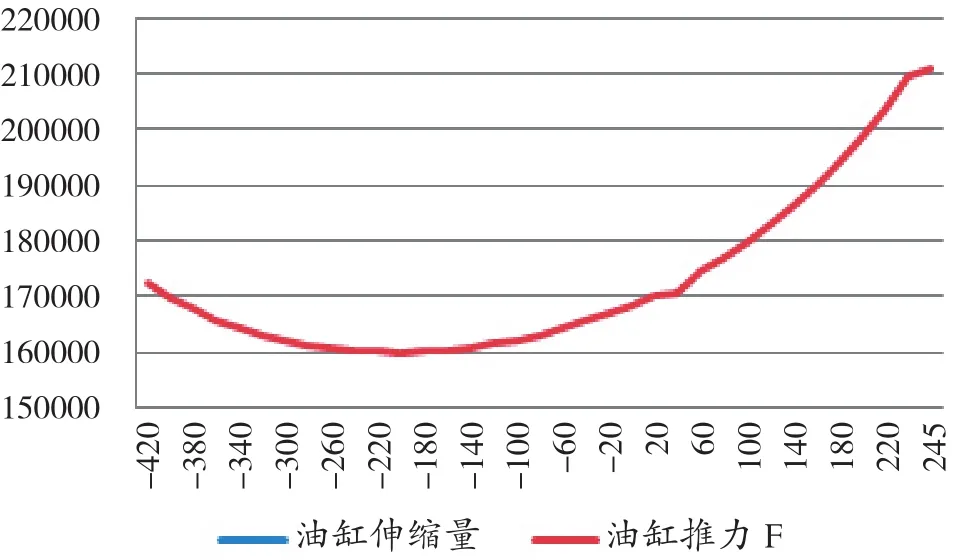
图3 油缸推力与伸缩量关系图
由图可知,在转向油缸伸出最大位置时油缸推力为最大Fp=2.1e5N。
3.2.2 侧向冲击受力计算
前文所述,前轮受到阻碍物并发生偏转时,油缸内最大压力为24MPa,所以转向臂上轴承受到油缸的反向的载荷也为24MPa。
油缸轴承处载荷:

其中S为转向油缸活塞作用面积,S=0.02m2。
代入上式得:F1=4.8e5N。
转向横拉杆轴承处载荷:

其中l为横拉杆轴承阻力臂,l=0.96m.
代入上式得:F2=54122N。
4 转向臂有限元建模
4.1 转向臂几何建模
该型号矿用自卸车转向臂的结构形状设计较为复杂,结构不规则,本文将采用 SolidWorks三维建模软件完成转向臂的实体建模,在建模过程中,本着尽量贴合实际的原则,对一些如:螺栓孔、轴承压盖等次要的特征进行了简化,以便于模型后续的分析。如下图4所示,为在SolidWorks软件中建立的转向臂几何模型,转向臂通过12个M42螺栓与前轮轴相连,又通过2个关节轴承分别与转向油缸、转向横拉杆连接。

图4 转向臂几何模型
4.2 创建转向臂有限元分析系统
建立转向节的有限元模型是进行有限元分析的前提,并且有限元模型质量的高低直接影响到后续计算的精度。在三维建模软件SolidWorks中所建转向臂模型导入到Workbench软件后,检查模型,确认是否有信息丢失现象,没有信息丢失说明导入的模型是真实可靠的。定义好材料数据,建立有限元分析系统如下图5所示,项目A为优化前转向臂满载静止转向时分析系统,项目B为优化前转向臂受侧向冲击时分析系统,项目C为优化后转向臂满载静止转向时分析系统,项目D为优化后转向臂受侧向冲击时分析系统。
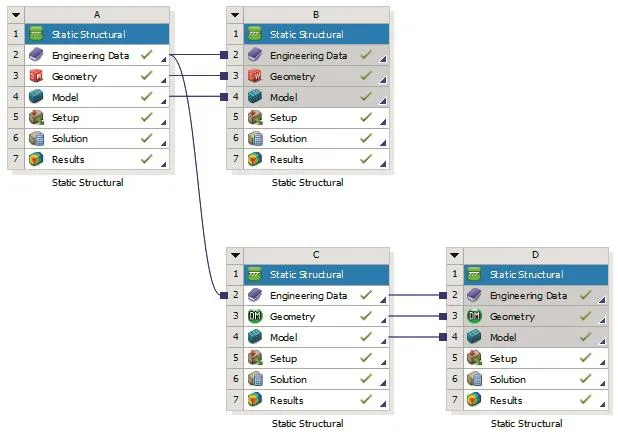
图5 有限元分析系统
在对几何模型划分网格时,要综合考虑计算精度和计算量,可根据实际计算需要选择不同的单元类型和单元密度[7-8]。本文中自卸车转向臂尺寸较大,形状复杂,因此,此处选择四面体单元,采用自动网格划分方法,对关节轴承安装孔及受力较大处进行局部网格细化,得到网格模型如图6所示。

图6 转向臂网格划分有限元模型
网格划分后利用 Workbench的网格检查工具检查所画网格的质量,对不满足要求的网格进行适当调整,最终评判网格质量较优,各单元评价结果如下图所示。
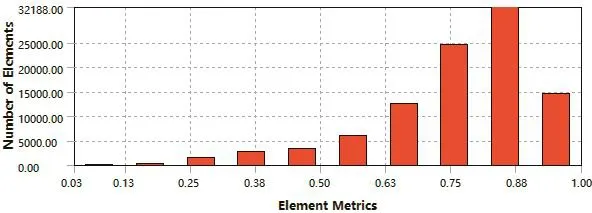
图7 各质量网格单元分布柱状图
4.3 转向臂的有限元分析
转向臂主要受力为转向油缸推力,平衡杆作用力及轮胎传递的地面反向阻力矩或侧向冲击力。对划分好网格的转向臂模型定义边界条件:在转向臂旋转中心处施加远程位移约束,在两个关节轴承孔配合面上施加轴承载荷。求解结果如下图所示。从图中可知转向臂未优化前转向臂应力集中位置与实际裂纹处相同,未优化前转向臂在受油缸推力及侧向冲击力时,最大应力分别为196.3MPa、470MPa。优化后转向臂在受转向油缸推力及侧向冲击力时,最大应力处位置变到轴承位置处,原最大应力处应力分别为154.7MPa、372MPa,应力明显下降。
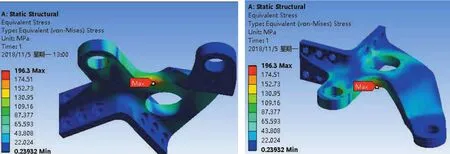
图8 未优化前油缸最大推力时转向臂等效应力云图
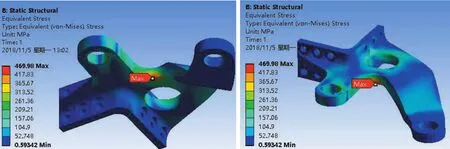
图9 未优化前轮胎侧向最大冲击力时转向臂等效应力云图
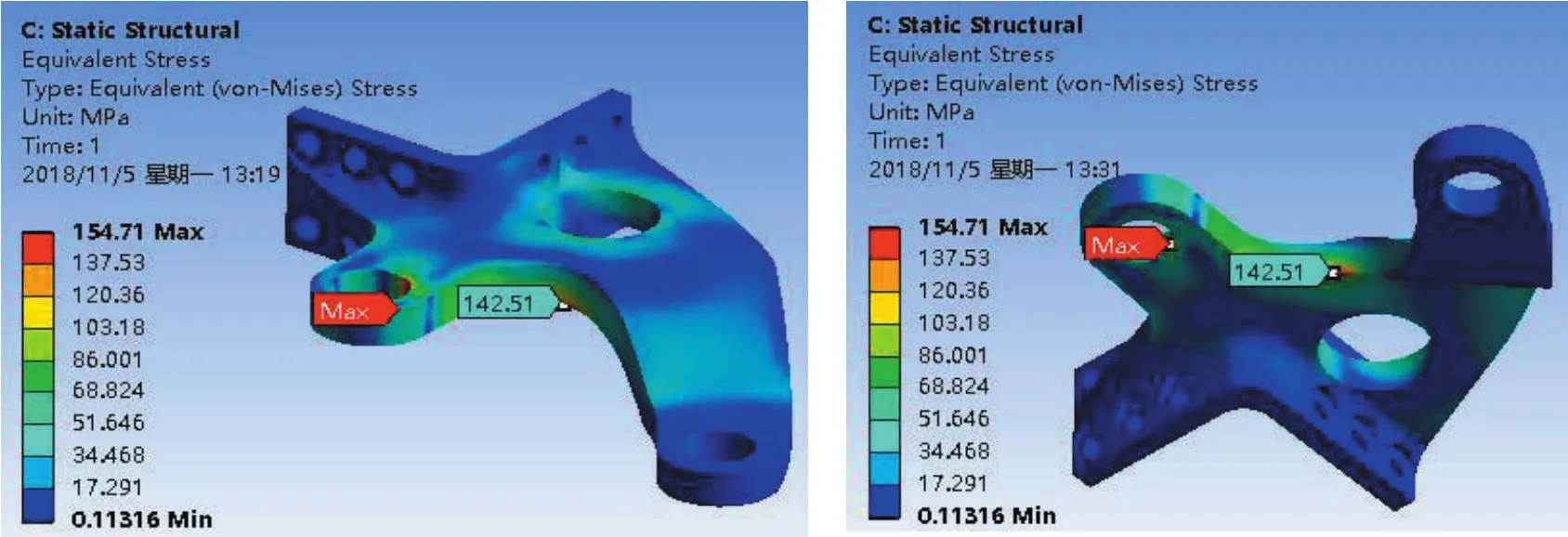
图10 优化后油缸最大推力时转向臂等效应力云图
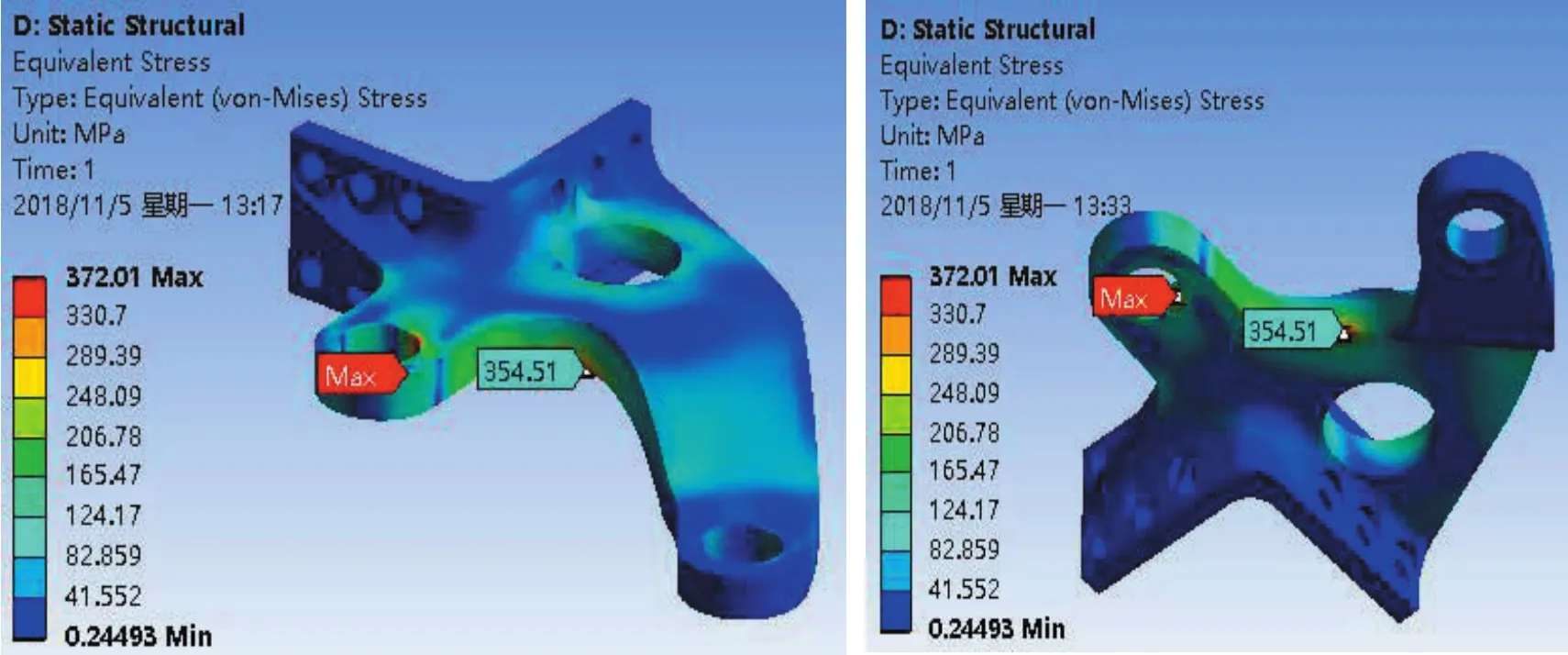
图11 优化后轮胎侧向最大冲击力时转向臂等效应力云图
5 结语
运用Workbench软件对转向臂在危险工况进行受力分析,得到转向臂应力分布云图,找出转向臂应力集中分布位置,并依此对转向臂进行优化,解决转向臂因应力集中产生微裂纹的问题。
