磁浮交通试验线压力管道直线度的测量方法研究及应用

韩 冰，刘成龙，杨雪峰

(1. 西南交通大学地球科学与环境工程学院，四川 成都 611756； 2. 西南交通大学高速铁路运营安全空间信息技术国方联合工程实验室，四川 成都 611756)

我国高铁的运营速度目前最高可达350 km/h，若在此基础上想要大幅提升运营速度，现有的高铁技术基本不可能完成。限制地面交通高速度行驶的根本因素是稠密大气，气动阻力与速度的二次方成正比，气动噪音随速度七次或八次方而剧增，这是地面上任何形式的交通工具都无法避免的客观规律[1]。然而，随着经济的发展和节能方面的考虑，地面超高速轨道交通的发展需求日趋强烈。国内外相关专家学者提出了超级高铁的概念，一致认为实现更高经济速度的最可能途径是采用真空管道磁浮列车[2]。

目前在建的西南交通大学真空磁浮高速列车试验装置是国内首个采用真空管道的磁浮交通试验线。该试验线的真空压力管道由12节直径约为4.2 m的金属管通过接缝焊接和外加法兰盘固定而成，重约900 t，全长约146 m。按照设计要求，12节金属管中心(圆心)的连线应在同一条直线上，但由于在管道加工和安装施工时均存在误差，各节管道的中心很难严格在一条直线上。在进行抽真空试验前，需要了解整个真空管道的直线度情况，若各节管道的中心在一条直线上，则说明真空管道的直线度较好。

由于各节真空管道中部空置，没有实物中心，因此无法直接确定各节管道的中心位置。此外，真空管道封闭，与外部无法通视，如何建立管道内高精度的三维控制网成为一个难题。结合工程实例，本文将研究并介绍真空管道内三维控制网的建立方法，以及各节管道圆心坐标的确定、整个真空管道圆心直线度的测量原理及其精度分析，为今后真空管道磁浮列车的相关试验及实际应用提供技术参考。

1 管道内三维控制网的建立方法

由于真空管内与外部无法通视，为测量各节管道的圆心并分析整个真空管道圆心直线度，需要在管道内部建立高精度的三维控制网。综合该真空管道内测量环境及精度方面的考虑，本文仿照高速铁路轨道控制网(CPⅢ)测量方法[3]，将管道内的三维控制点设置在金属管道两侧的内壁上，且成对布设，同时采用高铁CPⅢ测量标志[4]。考虑到后期需要对各节管道接缝处的圆心坐标进行测量，故沿大致平行于管道纵向的方向，布设了5对共10个控制网点，每对点纵向间距约35 m，如图1所示。

本文将管道内的三维控制网测量分为平面和高程两部分进行阐述，采用的测量仪器为徕卡TS60智能型全站仪。

1.1 平面控制测量

传统方法进行边角控制网测量时，通常在控制点上架设仪器，在其余控制点上摆放棱镜进行边角观测[5]。由于管道内的控制点均匀布设在管道的内侧壁上，无法像传统边角网那样进行边角测量，距离也只能进行单程测量。本文采用自由测站测量技术[6]，并使用全圆方向距离观测法对管道内的各个控制点进行边角观测，测量网形如图1所示。共进行了6个自由测站的测量，保证每个控制点被观测的次数不少于3次，相邻测站观测的相同控制点不少于两对。与传统的边角控制网测量方法相比，该测量方法具有测站位置选择灵活、多余观测数多、自动化程度高、能够消除对中误差等优点[7]。

为了后续可以方便地测量及分析各节管道的圆心坐标，同时为了更直观地分析各节管道圆心直线度情况，设计三维控制网坐标系的X、Y轴分别为真空管道的纵向和横向，Z轴垂直于XOY面，每个控制点的高程即为Z轴坐标。因此为建立项目的工程独立坐标系，选取管道左侧内壁上的控制点L1作为坐标原点，L5作为坐标系X轴的定向点。管道内平面控制网数据处理步骤及原理如下：

(1) 所有自由测站的边角测量外业结束后，首先进行平面控制网的自由网平差和精度评定，计算出所有控制点在假定坐标系下的平面坐标及其精度情况。

(2) 根据自由网平差后L1和L5的坐标，可以反算L1至L5间的坐标方位角α；由于设计L1至L5方向为坐标系的X轴，该边在设计坐标系中的坐标方位角为0，因此假定坐标系和设计坐标系间的旋转角为α，就可以将上述自由网平差后各点的坐标，采用式(1)逐一转换到设计坐标系中，得到各个控制点在设计坐标系中的坐标。

为了不改变自由网的网形及精度，本文采用三参数坐标转换公式[8]，设(x,y)为坐标转换后的坐标(设计坐标系)，(x0,y0)为坐标转换前的坐标(假定坐标系)，则三参数坐标转换模型为

(1)

式中，Δx、Δy和α分别为转换前后两套坐标系间的平移参数和旋转参数。在本例中坐标转换是以L1点进行的，因此Δx、Δy均为0。

1.2 高程控制测量

考虑到在管道侧壁的控制点上无法直立水准尺，本文采用基于自由测站观测值的间接高差测量技术[9]，建立管道内的高程控制网，且平面和高程控制点共桩。采用平面控制网自由测站测量的斜距和竖直角观测值建立管道内的三角高程网，这样可以做到外业全站仪各个自由测站的一次测量即可建立三维控制网。同时，平面坐标和高程共桩的好处是便于后续采用自由设站测量技术进行各节管道圆心三维坐标的测量。基于自由测站观测值的间接高差测量技术建立管道内三角高程控制网的步骤及原理[10]为：

(1) 管道内的三角高程网是在自由测站观测值的基础上建立的，且采用CPⅢ测量标志，因此测站至测点的三角高差不需要量测仪器高和棱镜高。

(2) 本文采用中间法三角高程的间接高差组建三角高程网。所谓的间接高差，就是根据测站到控制点间的直接高差相减得到的相邻控制点间的高差。下面以L1和R1点间的高差计算为例，介绍这两点间间接高差的计算原理，其他相邻控制点之间的间接高差计算原理与之类似。

设控制点L1和R1之间的高差为h，测站到L1、R1点的斜距及竖直角分别为S1、S2和V1、V2，则L1和R1间的间接高差为

h=S1sinV1-S2sinV2+f1-f2

(2)

式中，f1、f2分别为自由测站观测L1、R1点时的地球曲率和大气折光对直接高差的影响值[11]。若令D1=S1cosV1，D2=S2cosV2，则式(2)可写成

(3)

如图1所示，管道内各个自由测站测量相邻控制点时的距离大致相当，因此D1≈D2=D，而同一个测站测量L1和R2时又是在同一环境条件下进行的，则有K1≈K2≈K，综上则有f1≈f2=f，因此L1、L2两点间的间接高差为

h=S1sinV1-S2sinV2

(4)

可见相邻点的间接高差中既没有仪器高和棱镜高的量测误差，也抵偿了绝大部分球气差的影响。

(3) 按照上述思路和原理，基于6个自由测站的观测值，可以形成如图2所示的三角高程控制网。由于每个控制点至少有3个自由测站对其进行观测，因此用自由测站到控制点间的直接高差计算得到的两个相邻控制点间的间接高差，每两个相邻控制点之间至少有2个以上的间接高差观测值，存在多余观测，可以以L1为高程起算点，采用严密平差的方法计算出管内所有控制点的高程并进行精度评定。

2 整个管道圆心直线度测量及其分析方法

由于真空管道中部空置，无法直接准确地获得各节管道的圆心坐标及半径，只能先使用测量仪器采集每节管道接缝处内侧同一个圆周上若干个离散点的坐标，再通过圆曲线拟合方法求出各节管道的圆心坐标及半径。本文结合现场测量环境，提出一种基于智能型全站仪无棱镜测距模式的真空管道圆心直线度测量方法，最终实现了整个真空管道圆心直线度的测量及分析。

2.1 管道接缝处内侧圆周上离散点坐标的测量方法

依据管道内的三维控制网，本文采用自由设站的方法测量每节管道接缝处内侧同一个圆周上离散点的三维坐标，测量原理及方法[12]如下：

(1) 首先依据三维控制网进行自由设站测量，并对设站精度进行评定。如图3所示，在设站点N上利用智能型全站仪观测该设站点到4个已知控制点的水平方向、天顶距和斜距观测值；然后将点N的三维坐标及其定向角的平差值作为未知参数，根据极坐标原理计算点N的三维坐标和定向角的近似值，据此计算点N到各个已知点的近似坐标方位角和边长；最后根据间接平差原理开列误差方程和法方程，解算法方程得到点N的三维坐标(XN,YN,ZN)和定向角平差值ω，并计算出点N在X、Y、Z坐标轴方向上的坐标中误差及定向角中误差。本项目所有自由设站测量的精度最值统计见表1。

(2) 在自由设站测量精度满足要求后，采用无棱镜测距模式(TS60智能型全站仪无棱镜测距的精度可以达到2 mm+2 mm/km)，观测每节管道接缝处内侧同一个圆周上各个离散点的水平方向值LNP、天顶距ANP、斜距SNP，则离散点的三维坐标计算式为

(5)

每个圆周上至少测量8个以上离散点的三维坐标，由于无法保证测量得到的各个离散点都严格在同一条圆曲线上，因此为确保后续圆心坐标的拟合精度，在采集离散点坐标时，同一个圆周上各个离散点的X坐标较差绝对值应该控制在5 mm以内。

2.2 各节管道圆心坐标及半径的计算方法

由于真空管道纵向轴线方向与X轴方向平行，因此同一个接缝处的圆周上各点的Xi坐标应该相等，其值相当于线路测量时的断面里程。对于同一断面内各点的(Y，Z)坐标而言，其在指定断面内可采用二维拟合的方法，计算出各节管道接缝处圆截面的圆心坐标(Yi，Zi)及半径Ri，则此圆心在三维坐标系中的圆心坐标为(Xi,Yi,Zi)，Xi的值可以用采集到的该截面圆周上所有离散点X坐标的平均值表示。

目前，最小二乘拟合是圆曲线拟合中过程最复杂、拟合精度最好的一种方法，其常用的方法主要有两种：常规最小二乘拟合和正交距离最小二乘拟合。前者以圆曲线的参数方程为基础，但该方法不适合在局部内采集离散点且离散点分布不均匀的情况，如在1/2圆、2/3圆等情况下采集数据的状况[13]。由于该试验线的真空管道内部铺设有轨道等设施，无法均匀地测出接缝处圆周上的离散点，此时若只采用常规最小二乘法求得圆心坐标及半径，则与实际值相差较大，拟合效果不佳。

因此，本文采用以各离散点至拟合圆曲线距离的平方和最小为准则的正交距离最小二乘圆曲线拟合方法，同时结合迭代法，经过多次迭代求解，直至达到最佳拟合效果。采用迭代法还可以解决圆曲线拟合过程中，因采集到的局部离散点分布不均匀而导致拟合精度不高的状况[14]。

(6)

式中,X0代表参数(a0,b0)和r0的初始值。以采集到的所有离散点y坐标和z坐标的平均值作为圆心坐标初始值(a0,b0)，各离散点到该初始圆心的几何距离之和的平均值作为半径的初始值r0。

根据正交距离圆曲线拟合准则，设在圆曲线上采集的离散点到拟合圆心之间的几何距离与拟合后的圆曲线半径之差为di，若将di设为观测值，则可以列出观测方程

(7)

(8)

(9)

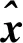
(10)

由参数的协因数阵，可求出参数的中误差

(11)

在实际外业测量中，很难保证均匀地采集圆周上的离散点，若只进行一次正交距离最小二乘拟合，可能达不到理想的拟合效果。为了提高圆曲线拟合精度，应在模型中引入迭代法[16]，不断重复，直至满足下式的要求

(12)

经过在Matlab中编译上述模型所生成的程序，计算得到各节管道的圆心坐标、半径拟合结果及其相关精度指标，见表2。

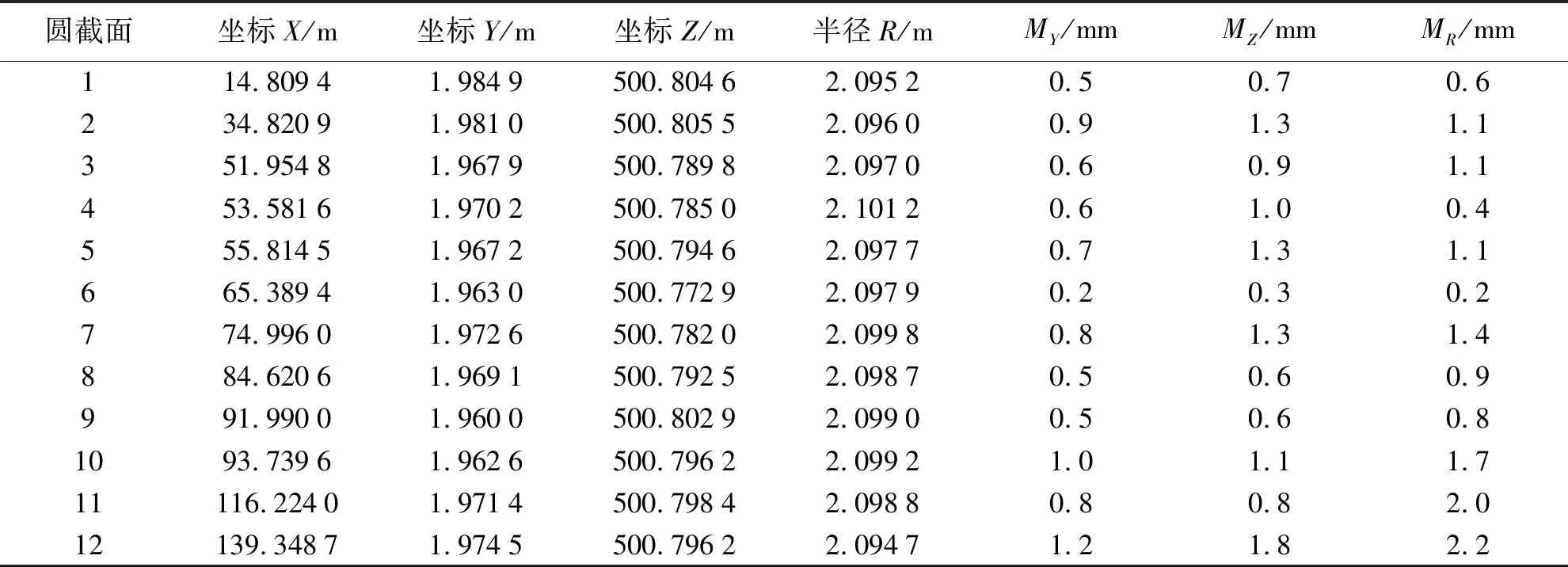
表2 各节真空管道的圆心坐标和半径拟合结果

由表2可知，拟合得到的12节真空管道的圆心Y、Z坐标及半径R的中误差最大值分别为1.2、1.8、2.2 mm，由此可知本文所阐述的真空管道圆心直线度的测量方法可行，精度和可靠性较高。

2.3 整个管道圆心直线度分析方法

在真空管道的安装及其后续的试验期间，科研人员最为关心的是各节管道间的横向直线度及高程方向的直线度。其中，各节管道间横向直线度可直接由拟合得到的各节管道圆心Y坐标较差得到，若各节管道圆心Yi坐标(i=1,2，…，12)变化不大，则说明各节管道在横向(Y方向)直线度较好；同理，若各节管道圆心在高程方向的Zi坐标(i=1,2，…，12)变化不大，则说明各节管道在竖向(Z方向)的直线度较好。本文利用实测得到的12节真空管道圆心的三维坐标，分别在平面(XOY)和竖面(XOZ)进行线性拟合，结果如图4、图5所示。经过统计12节真空管道圆心Y、Z坐标及半径R的极值，可知各节管道圆心Y坐标间互差最大值为24.9 mm，Z坐标间互差最大值为32.6 mm，各节管道半径间互差最大值为6.5 mm，基本满足设计的安装精度要求。

3 结 论

通过对磁浮交通试验线压力管道直线度测量方法的研究及其工程实践，得到以下结论：

(1) 通过自由设站测量精度的统计结果，说明本文方法建立的真空管道内三维控制网的精度较高；采用自由设站测量和极坐标测量相结合的方法，获取各节管道接缝处内侧圆周上各个离散点的三维坐标，测量方法精度高，测量数据可靠。

(2) 真空管道的内半径设计值为2.1 m，本文拟合出各节管道的内半径与其设计值最大差值为5.3 mm(包含管道的加工误差)，进一步说明该方法获取真空管道圆心坐标及半径的可靠性较高。

(3) 本文首次将高速铁路CPⅢ测量标志和全站仪自由测站、自由设站测量技术应用到真空管道圆心直线度的测量中，取得了较好的测量成果，可以为今后真空管道磁浮列车的建设提供参考。