等离子鞘套热力学波动对电磁波传播的影响

刘智惟，夏国江，邓永福，赵锦瑾，韩 明

(北京宇航系统工程研究所，北京 100076)

0 引 言

当飞行器在大气层中飞行时，会与周围空气剧烈摩擦形成等离子鞘套。等离子鞘套会造成电磁波的衰减和畸变，影响信号的正常传输，产生“黑障现象”[1]，干扰飞行器的正常测控通信。

为了缓解和攻克“黑障现象”，自20世纪60年代起，大量研究力量被投入于等离子鞘套中电磁波传播特性的研究[2-10]。在研究过程中，等离子鞘套通常被视为一种稳态的有耗介质。谢楷等人研究了L和S波段电磁波在等离子体中的衰减[11]，Petrin分析了电磁波与等离子鞘套之间的非线性关系[12-13]，Kim等分析了不同等离子鞘套条件下电磁波的衰减和反射[14]，Cerri等分析了电磁波反射特性与电子密度、等离子鞘套厚度间的关系[15]，Bai等分析了等离子鞘套中电磁波的极化特性[16]。

这些成果促进了等离子鞘套电磁波传播特性研究的发展,但稳态有耗介质的假设忽略了高速湍流流场所引起的鞘套动态变化,真实的鞘套是剧烈随机波动的[17-18]。这会造成其介电特性的波动，进而引起电磁波在其中的变化。这些变化会造成信号强度、相位等的变化，引起接收机无法有效提取测控信号、造成误码等现象，干扰信息的正常传输。近年来，已有研究开始关注这方面的问题[19-21]。为保证飞行器测控通信的可靠性，应当更加细致地研究等离子鞘套对电磁波的影响,以便针对等离子鞘套动态特性对电磁波的影响，开展无线通信体制设计，降低或消除其对通信信号的影响。

本文从等离子鞘套热力学参数波动的角度出发，分析等离子鞘套动态特性对电磁波的影响,可为等离子鞘套动态特性对电磁波影响的研究提供一个新的思路和方向。

1 等离子鞘套热力学参数波动与等离子鞘套介

电特性的关系

1.1 等离子鞘套热力学参数波动

在可压缩湍流理论中，流场热力学特征参数存在如下关系[17]：

(1)

在等离子体中，根据萨哈方程可知，电子密度波动与温度波动存在如下关系[22]：

(2)

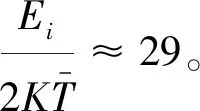
在钝头飞行器飞行条件下，测控通信天线周围的等离子鞘套的碰撞频率ν可由下式表述[23]：

ν=2.71×107PT-1/2

(3)

式中:压力P单位为Pa;温度T,单位为K。

根据式(3)，可得

(4)

对式(4)做变换得

(5)

(6)

1.2 等离子鞘套热力学参数波动与等离子鞘套介电特性

等离子鞘套的介电常数εr可表示为：

(7)

式中:ωp是等离子体频率。

(8)

式中：e是电子带电量；me是电子质量。

在电磁波频率不变的条件下，等离子鞘套介电常数的波动Δεr可以表述为：

(9)

根据式(9)可得，等离子鞘套介电常数波动与电子密度、碰撞频率及其波动间存在如式(10)关系。式(10)即为等离子鞘套中热力学参数波动与等离子鞘套介电常数波动间的关系。

根据上述算式，可以计算分析等离子鞘套中热力学参数的波动会对电磁波的透射系数和反射系数产生什么样的变化。

Δεr=

(10)

2 飞行器等离子鞘套模型

本文以典型飞行器RAM C-II为例，来分析等离子鞘套热力学参数波动对电磁波传播特性的影响。根据NASA相关技术报告可知，测控通信天线所在区域等离子鞘套电子密度和碰撞频率分布规律[24]如图1和表1[10]所示。本文以此作为平均电子密度和平均碰撞频率。

根据Lin等的研究可得，等离子鞘套的温度等参数的波动沿飞行器壁面法向方向变化，其变化规律近似服从双高斯分布，波动的峰值大致为ΔT·T-10.3[22]。

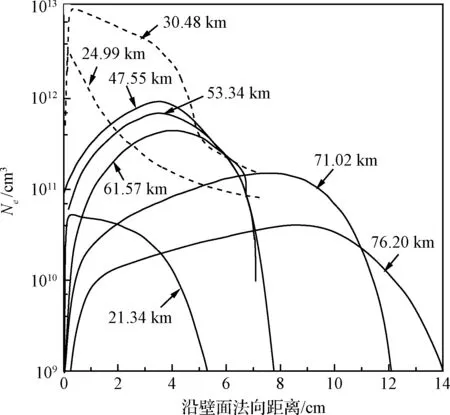
图1 RAM C钝头飞行器等离子鞘套电子密度分布图Fig.1 Electron density profiles at different altitudes from NASA RAM-C data

3 仿真结果及分析

考虑到S波段被广泛应用于测控通信、Ka波段被认为是缓解和突破黑障的有效手段，本文选取S波段2.3 GHz和Ka波段30 GHz作为算例来计算和分析等离子鞘套热力学参数波动会造成电磁波透射系数T和反射系数R如何的变化。计算式采用分层近似方法。用Ta和Ra来分别表示透射系数和反射系数的幅值。

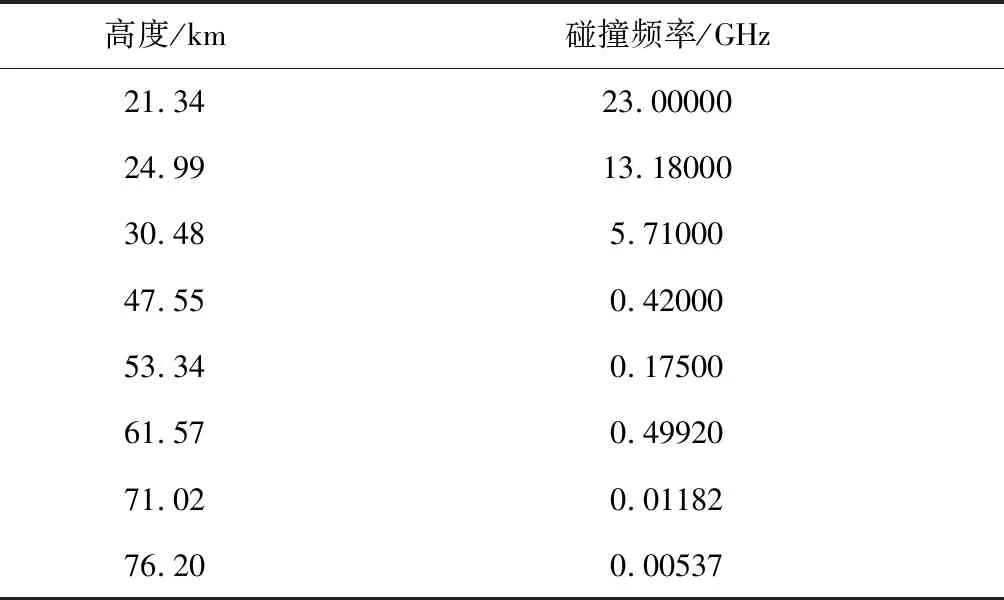
表1 不同高度下等离子鞘套的碰撞频率Table 1 Collision frequencies at different typical altitudes

分析等离子鞘套热力学参数波动对透射系数和反射系数幅值的影响，应当从对比有无考虑鞘套波动前后，透射系数和反射系数幅值的变化出发。因此，以Ta0和Ra0来分别表示没有考虑鞘套波动时的透射系数和反射系数幅值；以Taf和Raf来分别表示考虑鞘套热力学参数波动时的透射系数和反射系数幅值的峰值。以Trat=Taf/Ta0、Rrat=Raf/Ra0，来分析等离子鞘套热力学参数波动时，对电磁波透射系数和反射系数的改变程度。当Trat和Rrat等于1时，说明等离子鞘套的波动未造成电磁波透射系数和反射系数的变化；若Trat和Rrat偏离1，则说明等离子鞘套的波动引起电磁波透射系数和反射系数的变化，相应的也就引起电磁波透射功率和反射功率的变化。从透射系数及反射系数的定义，可以发现，根据Trat和Rrat，可以得到等离子鞘套热力学参数波动对电磁波透射功率PTrat和反射功率PRrat的改变：

(11)

3.1 均匀等离子体热力学参数波动对电磁波透射系数和反射特性的影响

考虑到钝头飞行器在大气层中飞行的全过程，等离子鞘套的厚度大致为10 cm左右，等离子鞘套环境的电子密度和碰撞频率参数范围为Ne∈(109cm-3,1013cm-3),ν∈(10 MHz, 50 GHz)。本文选取厚度为10 cm的均匀等离子体作为算例。其中，电子密度值分别选取Ne=109cm-3,1011cm-3和1013cm-3；碰撞频率值分别选取ν=10 MHz,1 GHz以及50 GHz。对均匀等离子体温度波动ΔT·T-1的幅度从0～0.3的情况下，相应波动下的Trat和Rrat。计算结果如图2至图7所示。由于Trat和Rrat是无量纲参数，因此图中纵坐标未标单位。

由图2至图4可得，在Ne=109cm-3时，热力学参数波动引起S波段电磁波反射系数的变化显著。波动状态下，Rrat最大可达6.5倍以上，对应功率变化约16.3 dB。随着波动幅度的增大，Trat也逐渐增大，并呈近似呈线性变化。随着碰撞频率的增大，热力学参数变化所引起的反射系数变化程度逐渐减小。热力学参数波动对S波段电磁波透射系数的影响微弱，最大不到0.09，对应功率变化不到0.82 dB。

在Ne=1011cm-3时，热力学参数波动对S波段Trat和Rrat的影响，随ν的变化呈不同特点。在ν为10 MHz和1 GHz时，波动对透射系数的影响十分显著：ΔT·T-1约为0.05时，Trat值趋近于0，功率接近消失。ν为50 GHz时，Trat相较10 MHz和1 GHz时明显减小，Trat的变化不到0.3，对应功率3.1 dB。且透射系数随热力学参数波动幅度变化的速度较10 MHz和1 GHz时缓和。

ν为10 MHz时，波动对Rrat的影响不明显。最大变化幅度不到0.005，对应功率仅为0.043 dB。ν为1 GHz和50 GHz时，波动对Rrat的影响开始显现，变化程度随波动增大而增大。1 GHz时最大为1.3，对应功率2.28 dB；50 GHz时最大为2.3，对应功率7.23 dB。

Ne=1013cm-3时，热力学参数波动对S波段Trat的影响十分显著。ν为10 MHz和1 GHz时，ΔT·T-1不到0.01就会使Trat趋近于0；ν为50 GHz时ΔT·T-1约0.08也会使Trat趋近于0。对Rrat的影响，在ν为10 MHz和1 GHz时十分微弱，Rrat的变化最大不到0.008，对应功率不到0.07 dB。在ν为50 GHz时，Rrat最大1.25，对应功率1.94 dB。

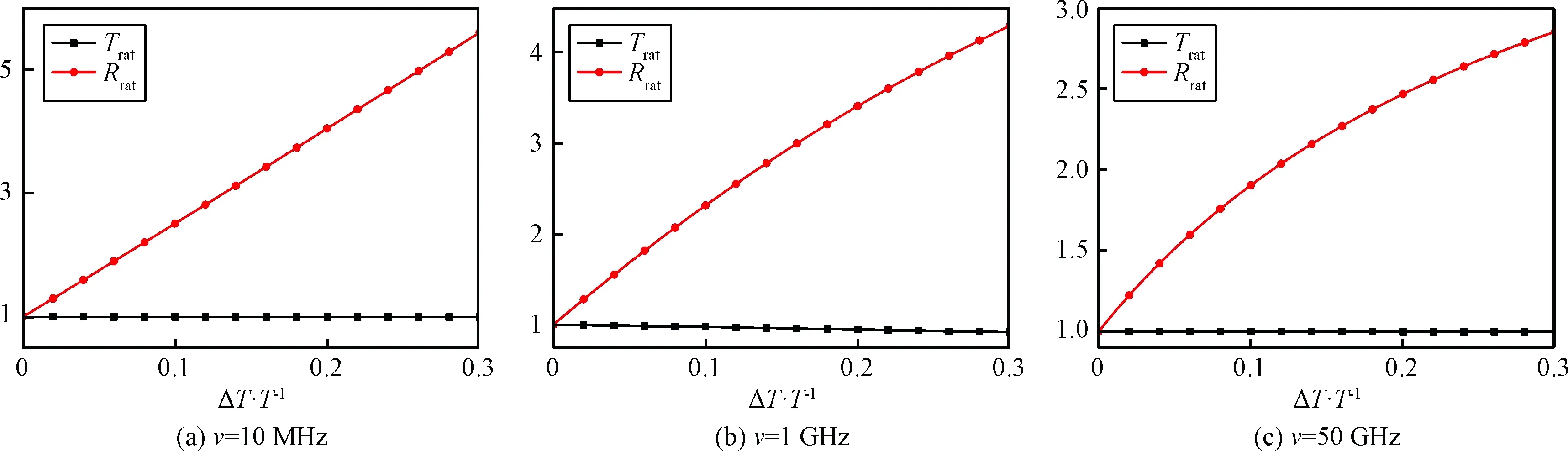
图2 Ne=109 cm-3时热力学参数波动引起S波段2.3 GHz电磁波透射和反射系数的变化Fig.2 Fluctuation effects at S-band when Ne=109 cm-3

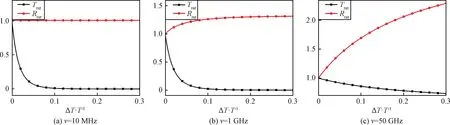
图3 Ne=1011 cm-3时热力学参数波动引起S波段2.3 GHz电磁波透射和反射系数的变化Fig.3 Fluctuation effects at S-band when Ne=1011 cm-3

整体上看，随电子密度的增大，热力学波动引起的反射系数变化减小，透射系数变化增大。在Ne=109cm-3时，碰撞频率增大，反射系数变化减小。Ne=1011cm-3和1013cm-3时，碰撞频率增大，反射系数变化增大，透射系数变化减小。

由图5至图7可得，在Ne=109cm-3时，热力学参数波动对Ka波段Trat的影响非常微弱，变化幅度最大不到0.004，对应功率不到0.035 dB。波动对Rrat的影响明显，波动幅度的增大会使Rrat增大。ν为10 MHz和1 GHz时，变化几乎一样，Rrat最大可达3.8，对应功率11.60 dB。ν为50 GHz时，Rrat最大可达3.1，对应功率9.83 dB。

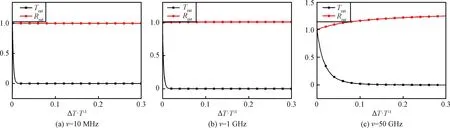
图4 Ne=1013 cm-3时热力学参数波动引起S波段2.3 GHz电磁波透射和反射系数的变化Fig.4 Fluctuation effects at S-band when Ne=1013 cm-3

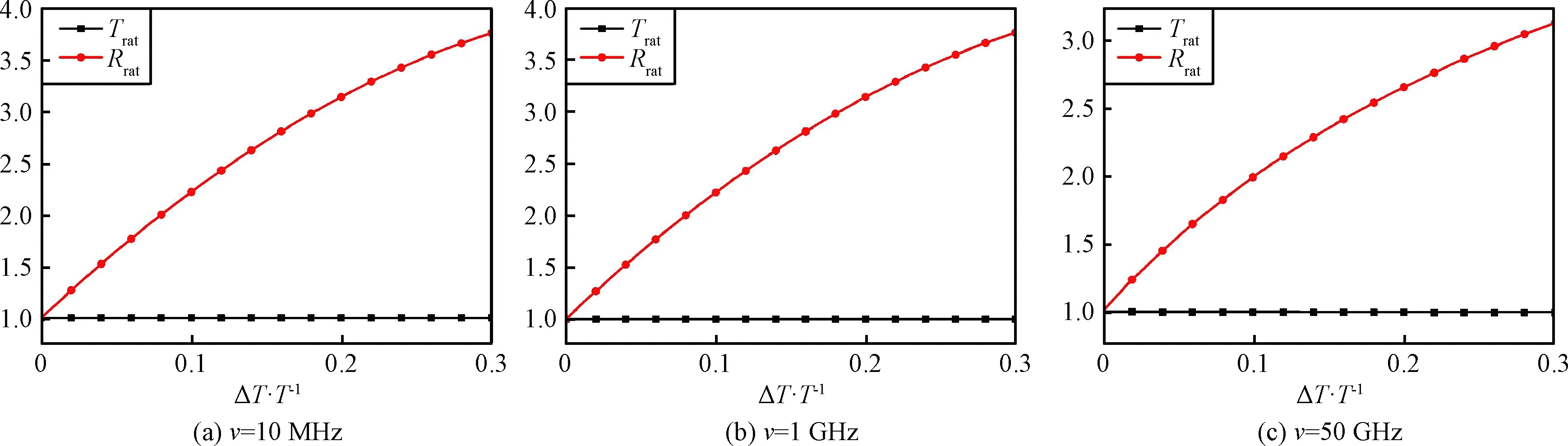
图5 Ne=109 cm-3时热力学参数波动引起Ka波段30 GHz电磁波透射和反射系数的变化Fig.5 Fluctuation effects at Ka-band when Ne=109 cm-3

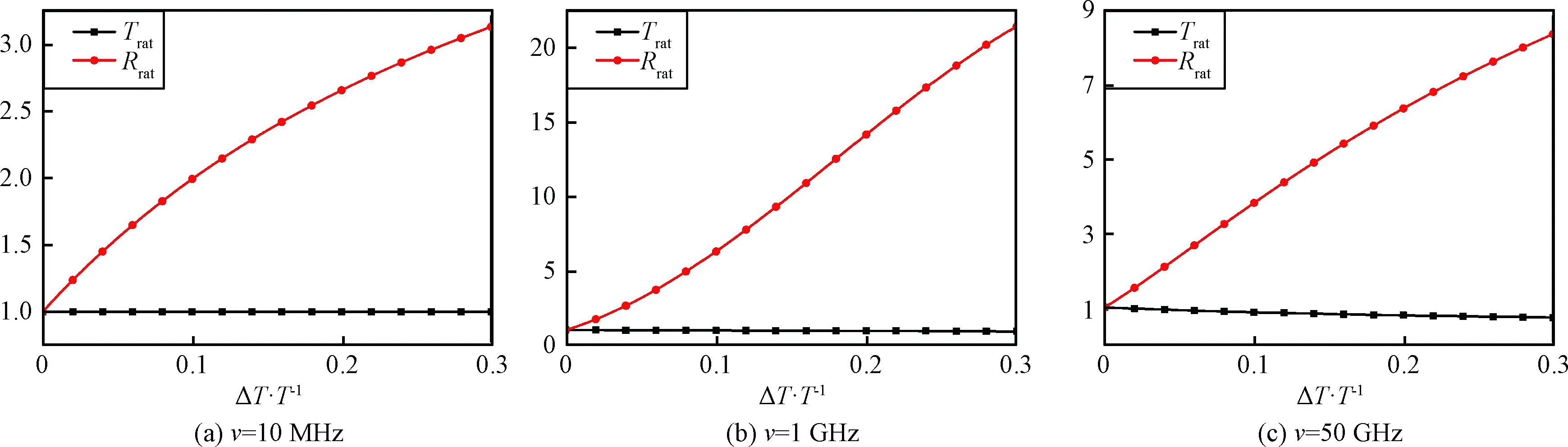
图6 Ne=1011 cm-3时热力学参数波动引起Ka波段30 GHz电磁波透射和反射系数的变化Fig.6 Fluctuation effects at Ka-band when Ne=1011 cm-3

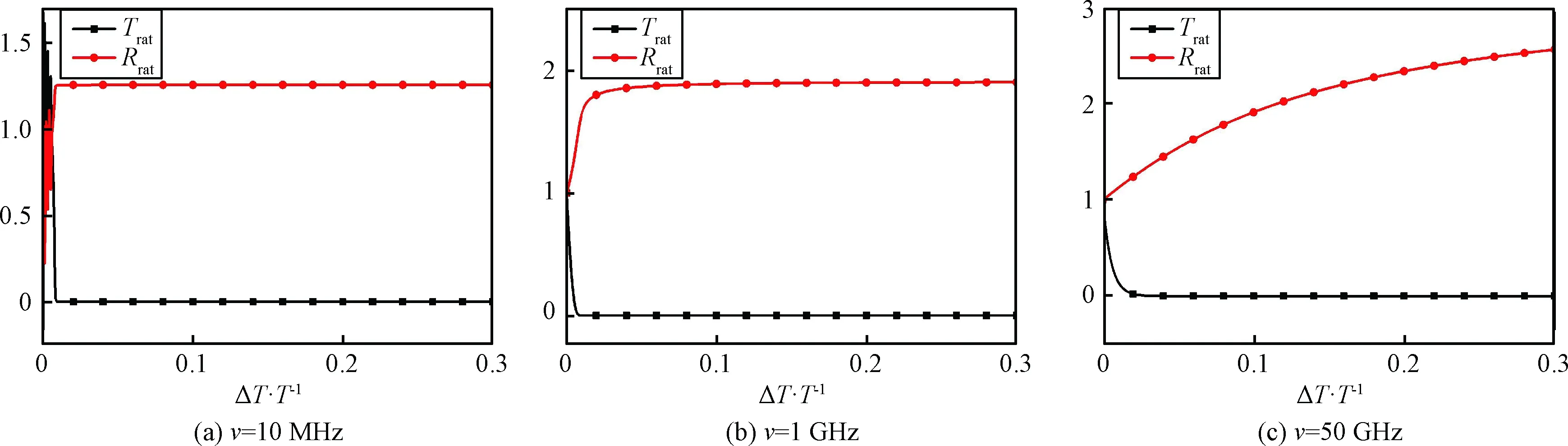
图7 Ne=1013 cm-3时热力学参数波动引起Ka波段30 GHz电磁波透射和反射系数的变化Fig.7 Fluctuation effects at Ka-band when Ne=1013 cm-3

在Ne=1011cm-3时，热力学参数波动对Ka波段Trat的影响不明显：ν为10 MHz和1 GHz时最大变化不到0.09，对应功率不到0.82 dB，仅在ν为50 GHz时，最大可引起可0.23的变化，对应功率2.27 dB。波动对Rrat的改变十分明显：ν为10 MHz、1 GHz、50 GHz时分别最大可达3、21和8，对应功率9.54 dB、26.44 dB和18.06 dB。

在Ne=1013cm-3,ν为10 MHz和1 GHz时，ΔT·T-1不到0.01就会使Trat趋近于0；ν为50 GHz时ΔT·T-1约0.02也会使Trat趋近于0。ν为10 MHz时，Rrat在ΔT·T-1增大至0.01后即稳定在1.25，对应功率1.94 dB。ν为1GHz时，Rrat在ΔT·T-1增大至0.025后即稳定在1.8，对应功率5.11 dB。ν为50 GHz时，Rrat随ΔT·T-1增大逐渐增大，最大为2.5，对应功率7.96。

整体上看，ν=10 MHz时，随电子密度的增大，热力学波动引起的反射系数变化减小，透射系数变化增大。ν=1 GHz和50 GHz时，随电子密度的增大，透射系数变化增大，反射系数变化先增后减。

3.2 RAM C II鞘套热力学参数波动对电磁波透射和反射系数的影响

真实飞行器等离子鞘套是非均匀分布的。分布特性受诸多因素影响。本文以RAM C II为例进行算例分析。等离子鞘套采用第三章节所介绍的模型。计算结果如图8所示。

由图可知，RAM C II飞行器在大气层中飞行的过程中，其等离子鞘套的热力学参数波动会引起电磁波透射系数和反射系数的变化。变化的程度随飞行高度的不同而不同。

对于S波段，随着飞行高度的增高，Trat由0.95(对应功率0.45 dB)逐渐减小，在30 km高度附近，趋近于0，直至70 km后逐渐恢复至0.1(对应功率20 dB)。Rrat由3(对应功率9.54 dB)逐渐在25 km处降至接近0，而后恢复到1附近(即没有功率变化)。直至高度升高至70 km，Rrat激增至10，对应功率20 dB。

对于Ka波段，随着飞行高度的增高，Trat由0.95(对应功率0.45 dB)逐渐减小，在30 km高度附近趋近于0。后迅速恢复，在43 km附近恢复至0.9(对应功率0.92 dB)。随后随高度增大逐渐恢复为1。Rrat由3.5(对应功率10.88 dB)逐渐在25 km处降至接近0。而后逐步增大，在60 km附近达到最大值16(对应功率24.08 dB)。随后又逐渐减小，在79 km附近减至1 km。

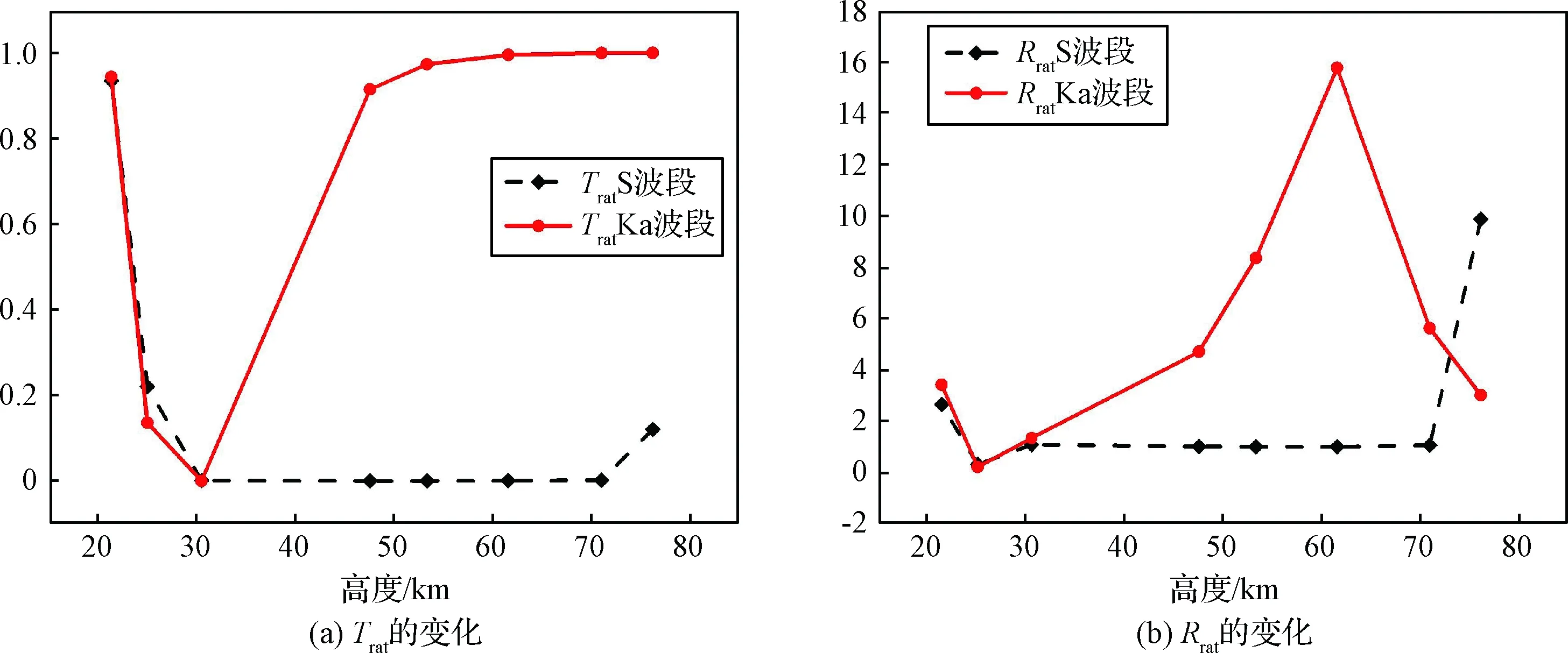
图8 不同高度下RAM CII鞘套热力学参数波动引起电磁波透射和反射系数的变化Fig.8 Effects of RAM C II fluctuation on wave propagation with different altitudes

4 结 论

本文结合可压缩湍流理论、等离子理论和电磁波理论来研究等离子鞘套热力学参数波动与等离子鞘套介电常数波动间的关系，及其对电磁波传播特性的影响。由仿真计算得：①热力学参数波动对随电子密度的增大，S波段反射系数变化减小、透射系数变化增大；Ka波段在碰撞频率10 MHz时，反射系数变化增大、透射系数变化减小，在碰撞频率1 GHz 和50 GHz时透射系数变化反射系数变化先增后减。②飞行高度会改变热力学参数波动的影响程度，随飞行高度增高，S波段透射和反射系数变化先减后增；Ka波段透射系数变化先减后增、反射系数变化先减后增而后再次减小。

由计算分析发现，热力学参数波动对电磁波透射和反射系数的改变，在不同环境下不尽相同。在工程应用中，建议针对遇到的实际等离子环境开展分析，获得波动包络范围，据此开展针对性设计以降低等离子鞘套对测控通信的干扰。