基于分离涡模拟的对转舵桨水动力性能数值分析

王志勇 范佘明 孙 群 张晨亮

（1.中国船舶及海洋工程设计研究院 上海200011；2.上海市船舶工程重点实验室 上海200011）

引 言

从几何外形上，对转舵桨主要由立柱、下齿轮箱体（从水动力角度舵桨与吊舱桨一致，故下齿轮箱体也可以称为吊舱），以及立柱前后各一个且旋向相反的两个螺旋桨组成。对转舵桨兼具全回转舵桨和对转桨的特点，能够绕立柱轴360°旋转，具有良好的操纵性。较常规舵桨而言，对转舵桨的后桨能够吸收前桨周向旋转能量，具有较高的推进效率。由于整个推进器的载荷由前后桨分担，在设计时可以减小两个桨的直径，因此对转舵桨具有良好的空泡和噪声性能，现已广泛应用于轮渡等船型上。对海洋平台而言，风浪条件常常剧烈变化，这就要求海洋平台作业时必须具有良好的定位能力。对转舵桨结合动力定位技术能够很好地满足工程实践需求，因此，对转舵桨具有广阔的应用前景。

对转舵桨的几何结构十分复杂，因此各部件之间的相互作用也非常复杂。但由于专利保护的关系，目前关于对转舵桨的研究资料非常少。舵桨和吊舱推进器在水动力外形上相似，两者之间的主要差别仅在于电机的布置方式不同，因此，关于吊舱推进器和常规对转桨的研究结果都具有参考价值。

近年来，随着对船舶快速性和节能减排的要求越来越高，研发设计高效的推进器一直是人们研究的重点。在吊舱推进器方面，周剑［1］进行了数值模拟和模型试验，结果发现吊舱和立柱导致了7.9%的推进效率损失。祝志超［2］对双桨式吊舱推进器的水动力性能进行了数值预报，给出了在不同偏转角度下的敞水曲线。在对转桨方面，前后桨之间的推力和扭矩表现出强烈的非定常性和周期性特征。由于后桨工作在前桨的尾流场中，后桨周围的流场表现出强烈的复杂性和非定常的特征，因此通常后桨的推力和扭矩难以准确预报。为提高数值模拟的精度，人们对影响数值计算精度的因素进行了大量研究。张涛［3］等采用MRF （moving reference frame）方法对对转桨的敞水性能进行数值模拟，结果表明：非定常效应不能忽略；当研究对象是对转桨时，采用准定常方法简化是不合适的。王展智［4］等研究了时间步长的影响，发现时间步长的选择取决于前后桨的叶数；当前后桨具有相同的叶数时，时间步长应该相对更小。

RANS模型是螺旋桨敞水性能预报中最常用的湍流模型。大量的研究结果表明，在预报单桨的推力和扭矩时，RANS模型已具有足够的精度。尽管如此，由于耗散的存在，无法得到桨叶后面流场的准确信息。相较于RANS模型，LES和混合LES/URANS模型精度更高，但需花费更多的计算资源。目前，采用计算资源需求适中的混合LES/URANS模型来取得相对精确的流场信息是一个可行的选择。

对转舵桨的水动力性能是工程实践中关注的焦点。此外，研究对转舵桨各部件之间相互作用的内在机理对优化设计能够起到帮助。本文采用IDDES结合滑移网格方法，对一组对转桨以及对转舵桨的水动力性能进行数值模拟，对两者的水动力性能进行对比；进一步对两者的推力系数进行频谱分析，分析对转舵桨振动特性以及各部件之间的相互作用。

1 IDDES方法简介

IDDES模型是在RANS和LES的基础上，经过一步步优化发展而来。湍流由各种大小和涡量的不同涡旋叠加而成，最大尺度的涡旋携带最多的雷诺应力，必须直接计算，而小尺度的涡旋对雷诺应力贡献不大，并且接近各向同性，可以采用模型简化［5］。理论上，可以采用DNS对全尺度范围的湍流进行直接求解，但受计算资源的限制，目前工程中还不可能采用DNS进行计算。而RANS在处理湍流动能上耗散很大，在预测非定常湍流方面存在不足。LES就诞生在这样的背景之下，其主要思想是通过空间滤波，滤掉小尺度的涡旋结构，并对其进行模型简化，对大尺度的涡旋结构进行直接模拟。因此，在解析尺度方面，LES介于RANS和DNS之间。然而，对于壁面附近的流动，黏性作用占主导，不存在惯性子区，因此LES在壁面附近要求的网格量理论上与DNS一致。如果不使用壁面函数，为使边界层内流场有效求解，物体周围无因次的第一层网格厚度y+通常要在1以下，这严重制约了其在工程上的应用。

为解决RANS在预测非定常湍流方面的不足，同时解决LES在近壁面附近网格数量要求非常高的问题，将两者结合起来是一个较好的解决方案。假定流体不可压缩，经过空间滤波后的质量和动量方程如下：

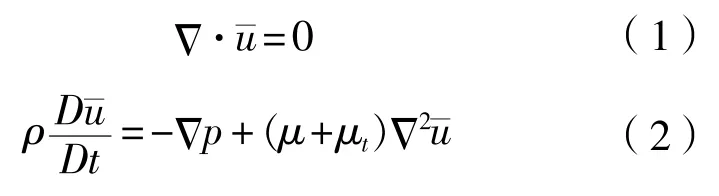
式中：ρ代表密度，kg/m3；上划线代表空间滤波。而采用时间平均之后N-S方程与滤波之后的N-S方程具有相同的数学形式，这是LES和RANS能够得以结合起来的数学基础。

SPALART等学者利用LES和RANS的控制方程在数学形式上相同的特点，发挥两者的优点，同时回避两者的缺点，巧妙地将LES和RANS结合起来，并于1997年提出了DES（detached eddy simulation）模型，通常称为DES97。DES97的主要思想是在近壁面和亚格子区域采用Spalart-Allmaras（S-A）模型进行计算，在远场采用LES进行计算，LES/RANS之间的切换通过引入一个长度尺度来实现。DES97对长度尺度 定义如下：

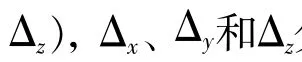
式中：d为离壁面最近的距离，分别是三个方向上的局部网格尺寸。CDES为常数，通常取0.65。

但在实践中，人们发现RANS与LES之间的切换，完全取决于网格尺度大小，在某些情况下，RANS会提前切换到LES，出现模化应力耗散（modeled stress depletion， MSD）的现象，从而导致网格诱导分离（grid-induced separation， GID）的问题。此外，DES97还存在速度型偏离对数率（log layer mismatch， LLM）的问题。针对GID，SPALART在 2006年又进一步提出 DDES［6］（delayed detached eddy simulation）模型。DDES对长度尺度进行修改：

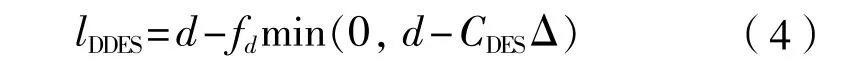
式中：fd为延迟过渡函数。

fd能避免LES在边界层内求解，从而解决GID问题。

针对LLM问题，TARVIN［7］在2006年又提出IDDES（improved delayed detached eddy simulation）模型，并在2008年，由SHUR［8］进一步发展出一种融合DDES和WMLES（wall modeled LES）的方法。

IDDES不仅可以与S-A湍流模型结合，也可以与其他的两方程模型（如SSTk-ω模型）结合。本文采用的是基于S-A湍流模型的IDDES模型。

2 几何模型和边界条件

2.1 几何模型

数值模拟的对象是MILLER［9］设计的一组4X4 的对转桨，记为 CRP6。CRP6 由 DTMB3686和 DTMB3687A 组成。前后桨之间的轴间距为0.043 2 m。另外，本文设计了一组吊舱和立柱，与CRP6共同组成了对转舵桨（CRRP）系统。立柱是剖面为NACA66mod并且无拱度的机翼。CRP6和CRRP的外形见图1。

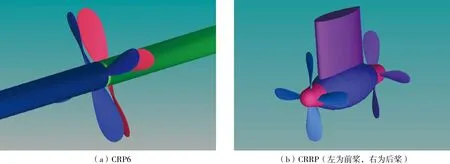
图1 计算模型

CRP6的主要几何参数如表1所示。

表1 CRP6主要几何参数

2.2 计算网格和边界条件

网格利用ANSYS ICEM 16.0 生成。如图2所示，整个计算域分为三部分：绕前后桨周围的两个旋转区域，包含立柱和吊舱以及远场的静止区域。静止区域是一个正方体，其长、宽、高分别为10DF（前桨直径）、6DF，、6DF。吊舱中心距上游入口为4DF，距下游出口为 6DF。CRP6的计算域与CRRP的计算域基本一致。时考虑到吊舱、立柱和两个旋转区域。这两个因素使分块的布置较困难。为获得网格质量高的六面体网格，分块必须尽可能布置为正六面体。常规的Y形切分由于会在近旋转域附近产生负网格，因此不能满足网格质量要求。一种可行的方法是对吊舱进行两次O形切分，对立柱进行两次Y形切分，分成6个六面体。图3提供了一种合适的分块布置，CRP6和CRRP的计算网格如图4 所示。

图2 计算域

计算域的各部分均采用结构化六面体网格。由于前后桨所在的旋转域在生成静止区域网格的时候必须删除，在布置吊舱和立柱周围的分块时必须同

图3 立柱和吊舱周围的分块布置

图4 计算网格

在物面附近，y+取40，边界层网格为10层。每片桨叶所在区域网格在100万左右，立柱和吊舱所在的静止区域网格数目约为200万，总网格数量为1 000万左右。

边界条件为：入口速度设为来流速度，压力梯度为0；出口速度设为0梯度，压力设为0；桨叶、吊舱以及立柱表面设为不可穿透物面条件；除入口和出口外，远场边界设为对称性边界。

3 计算结果与分析

3.1 CRP6

首先进行CRP6的敞水性能计算，并与MILLER在1976年试验报告提供的试验数据［9］作比较，以验证数值方法的可行性。计算时，前后桨的转速均取为720 r/min，与试验时相同。时间步长设为0.000 115 74 s，对应于每转720个时间步。进速系数为0.5～1.1，其通过改变来流速度而改变。进速系数、推力和扭矩系数等参数定义如下：

进速系数：

前桨推力系数：

前桨扭矩系数：

后桨推力系数：

后桨扭矩系数：

推进器推力系数：

推进器扭矩系数：

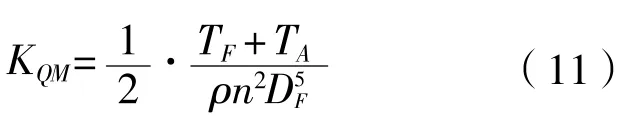
推进器敞水效率：

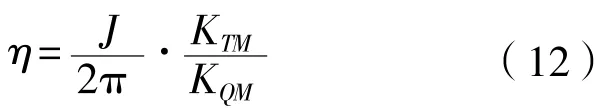
上述式中：VA为进速，m/s；n为转速，r/min；T为推力，N；Q为扭矩，N·m；下标F和A分别为前桨和后桨。为了方便作图，KTM和KQM分别定义为总推力和总扭矩的一半。

图5 CRP6 敞水特性曲线

图5是CRP6敞水性能的计算结果与试验结果的对比。前桨的计算结果与试验结果吻合良好，推力和扭矩的误差均在2%左右。后桨推力较试验结果低6%左右，扭矩高4%左右。整个推进器的推力误差在3%左右，扭矩误差在2%左右，效率的误差在5%左右，与试验结果吻合较好，证实本文采用的数值方法基本可行。

3.2 CRRP

MILLER设计CRP6主要是为研究对转桨前后桨之间的相互干扰，前后桨的桨叶数目相同时，更容易产生共振。为研究CRRP各部件之间的相互干扰，设计一套吊舱和立柱，加上CRP6，这四个部分，共同组成整个CRRP系统。

CRRP的前后桨转速与CRP6相同，均为720 r/min。时间步长设为0.000 115 74 s，对应于每转720个时间步。进速系数为0.5～1.1，通过改变来流速度来调节进速系数。推力系数、扭矩系数等参数定义基本与CRP6相同，但由于吊舱和立柱的存在，其中一些系数存在差别，其定义如下：

吊舱单元轴向力：

吊舱单元横向力：

推进器推力系数：

式中：下标pod代表吊舱和立柱。

图6是CRRP的敞水性能曲线。由图6（a）可以看出：随着进速系数增大，前桨和后桨的推力系数和扭矩系数都减小，并且后桨的推力和扭矩系数减小得更快。吊舱和立柱单元的横向力和轴向力系数如图6（b）所示。在0°舵角工况下，吊舱和立柱单元的横向力是一个接近于0的小量。随着进速系数增加，吊舱和立柱所受的轴向力基本不变。由于和CRRP推力的方向相反，这部分力造成了CRRP系统的效率损失。

图6 CRRP的敞水特性曲线

吊舱和立柱表面压力分布如下页图7所示。由图7（a）可以看出，立柱前端同时存在一个高压中心和低压中心，这个现象是由于前桨尾流场的周向旋转运动造成的。由于后桨的抽吸作用，立柱的后端产生一个低压中心，如图7（b）所示。立柱和吊舱的压力差同时作用，即产生压差阻力。压差阻力是吊舱和立柱轴向力的主要部分，粘性阻力只占其中很小一部分。

图7 J= 0.9时吊舱和立柱表面的压力分布

涡旋结构采用Q准则［10］定义，Q=500等值面如图8所示。从图中圆圈标出的部分可以看出，在立柱的前端存在明显的回流，这就解释了为什么在立柱的前端同时存在高压中心和低压中心。这种流动结构不仅会造成CRRP系统的推进效率损失，严重情况下，在低压中心附近还可能产生空泡，在工程实践中，应该尽量避免这种情况发生。随着涡结构靠近后桨盘面，前桨的梢涡逐渐收缩，在经过后桨之后，前桨的梢涡被打碎，形成网状涡。后桨的梢涡受前桨尾流的影响，存在一定程度的变形，但整体形状并未被破坏。

图8 Q = 500等值面

3.3 CRP6 和CRRP的敞水性能比较

CRP6和CRRP 的敞水性对比如表2所示。CRRP前桨的推力和扭矩系数明显高于CRP6，后桨的推力系数两者基本一致，而CRRP的扭矩系数略大于CRP6。整个推进器方面，尽管CRRP前桨推力系数大于后桨，但由于吊舱和立柱阻力的存在，CRRP整个推进器的单元推力小于CRP，扭矩系数则大于CRP。CRRP推进器推进效率比CRP小6%左右。

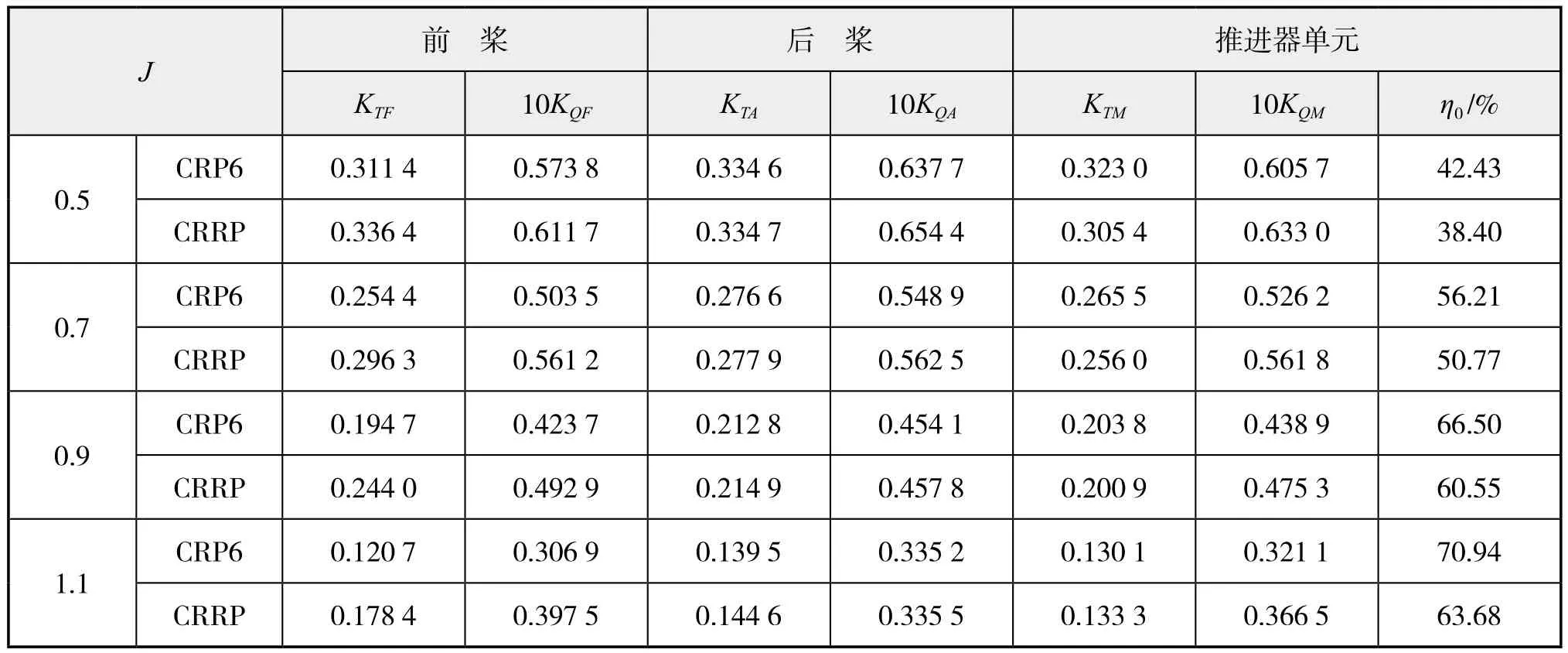
表2 CRP6和CRRP的敞水性能比较

3.4 CRP6 和 CRRP 各部件之间的相互干扰

图9 CRP6和CRRP推力扭矩系数变化曲线

吊舱和立柱的存在改变了前后桨之间的相互作用。图9是J= 0.9时CRP6和CRRP的推力和扭矩系数在旋转一周内的时历曲线，这些系数取自CFD计算结果。由图9（a）可以看出，CRP6前桨的推力扭矩系数有8个周期，而CRRP前桨的推力扭矩系数仅有4个周期。CRP6推力和扭矩的变化幅值都比CRRP大。在图9（b）中，CRP6和CRRP后桨的推力扭矩均具有8个周期，CRP6的系数随时间变化更快，但变化幅值比CRRP小。图9（c）是吊舱和立柱所受的轴向力和横向力系数的时历曲线，这些系数在桨旋转一周内仅有4个周期。为进一步分析前后桨之间的相互作用，对CRP6和CRRP的前桨和后桨的推力系数进行了快速傅里叶变换（FFT）。根据STRASBERG［11］的研究结果，CRP推力和扭矩系数的波动频率由式（16）决定：

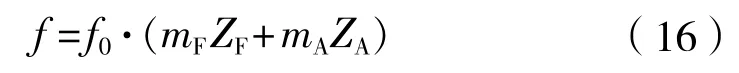
式中：下标F和A分别代表前桨和后桨；f0代表轴频；Z表示桨叶数目；m为整数，m和Z必须满足方程；mF ZF=mA ZA。

下页图10是CRP6和CRRP推力系数的频谱特性曲线。在图10（a）中，CRP6前桨推力系数峰值的频率为8倍轴频的整数倍，满足公式（16）。而CRRP前桨推力系数峰值的频率为4倍轴频的整数倍。从峰值上来看，CRRP前桨的峰值远小于CRP6，并且8倍轴频处峰值基本可以忽略。这意味着由于吊舱和立柱的存在，后桨对前桨的作用被弱化了，并且后桨周向诱导速度分量的影响可以忽略，轴向诱导速度分量是否有影响还需要进一步研究。由图10（b）可以看出，CRP6后桨推力系数幅值在6～7阶时仍较大，其基频为8倍轴频。而CRRP后桨推力系数幅值在5阶以后变得很小，其基频为4倍轴频。2阶幅值最大，频率为8倍（即前后桨叶数之和）轴频，说明前桨尾流的周向诱导速度分量对后桨有影响，两者之间产生共振。除前桨尾流导致的共振峰之外，后桨本身的运动也是其推力脉动幅值的主要部分。CRP6前桨和后桨推力系数的峰值分别为0.028 89和0.005 16，而CRRP前桨和后桨推力系数的峰值分别为0.006 86和0.013 44，吊舱和立柱的轴向力峰值为0.004 73。

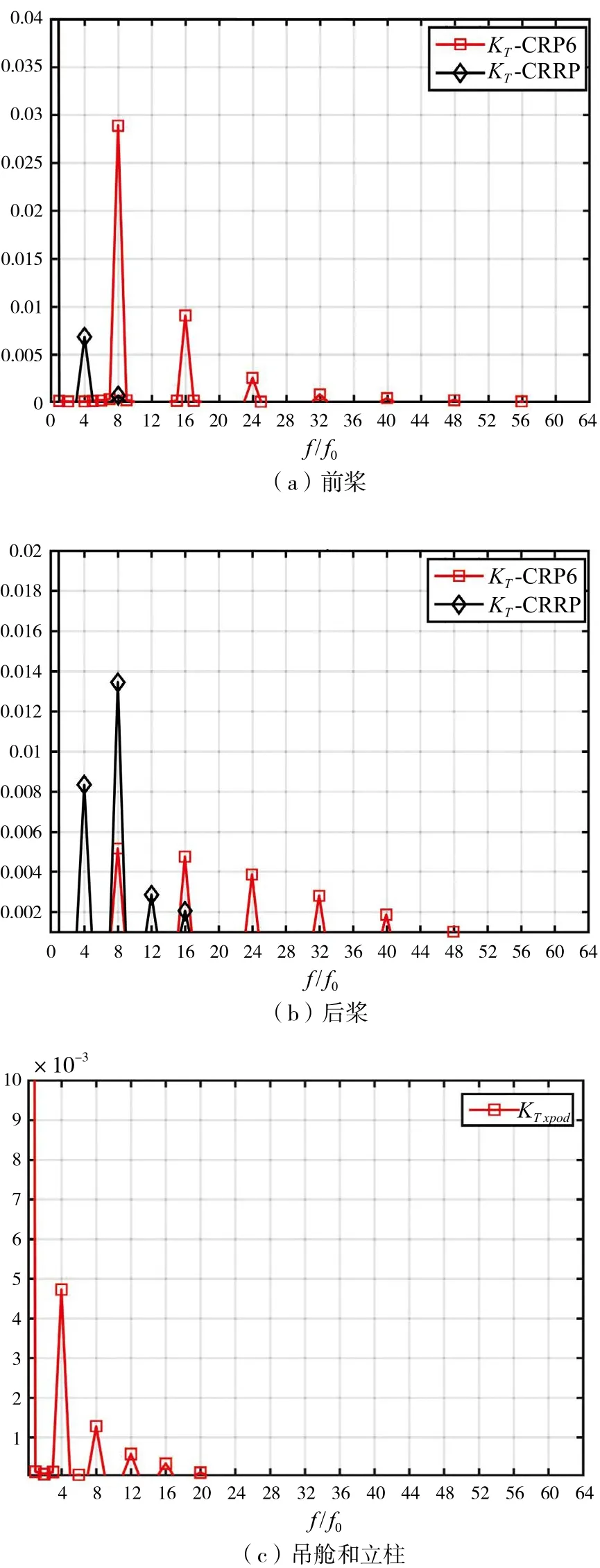
图10 CRP6 和CRRP推力系数的频谱分析

4 结 论

因此，尽管CRRP后桨的推力系数脉动幅值比CRP6大，但就推进器整体而言，CRRP推力产生的振动要比CRP6小得多。

本文设计了一套吊舱和立柱，与Miller设计的对转桨结合在一起，组成CRRP系统。运用滑移网格方法，结合IDDES模型，对CRP6和CRRP的水动力性能进行了数值模拟。通过比较CRP6的敞水性能计算值与试验值，验证数值方法的可行性。另外，为研究推进器各部件之间的相互干扰，对CRP6和CRRP的推力系数进行FFT变换。通过计算和分析，得到以下初步结论：

（1）比较CRP6的计算值与试验值，整个推进器单元的推力误差约3%、扭矩误差约2%、效率的误差约5%，与试验结果吻合较好，证明了本文采用的数值方法的可靠性。滑移网格方法结合IDDES模型，能够用来对CRP这种相互作用十分明显的复杂推进器的水动力性能进行数值预报。

（2）对CRRP进行水动力性能数值预报，并与CRP6进行对比。结果发现，CRRP前桨的推力和扭矩比CRP6前桨的推力和扭矩大，而两者后桨的推力扭矩则基本一致。吊舱和立柱阻力的存在使整个CRRP推进器单元的推力比CRP6小，而CRRP的扭矩则比CRP6大，导致CRRP的推进效率比CRP6小6%左右。

（3）吊舱和立柱阻力的主要成分是由其前后端的压力差产生压差阻力。在立柱前端存在明显回流，从而使立柱的前端同时存在一个高压中心和低压中心。这不仅会减小CRRP系统的推进效率，还有可能在低压中心附近产生空泡，工程实践中应该避免出现这种情况。

（4）吊舱和立柱的存在改变了CRRP前后桨的频谱特性曲线。前桨推力脉动幅值的频率不再满足公式（16），而是4倍轴频的整数倍。CRRP前桨推力脉动幅值比CRP6前桨明显减小。后桨周向诱导速度分量对前桨的影响基本可以忽略，但轴向诱导速度是否有影响则还需作进一步研究。就后桨而言，前后桨之间相互作用产生的共振依然存在，其自身运动产生的振动也是后桨脉动幅值的主要成分。但从整个推进器系统来看，CRRP推力的脉动幅值明显小于CRP6。相对于CRP，采用CRRP能够减小由轴承力导致的振动。

本文工作得到了本院吴琼和于海两位老师的指导，在此一并表示感谢。