基于DPSO-MKELM算法的风机齿轮箱轴承故障诊断

顾卫祥，王先发，徐靖楠，赵冰冰，童建强

（1.南京工程学院，江苏 南京 211167；2.国网安徽省电力有限公司东至县供电公司，安徽 池州 247200）

0 引言

随着经济的发展，世界各国对能源的需求与日俱增，大力推广可再生能源发电已成为共识，我国风能资源丰富，是未来可再生能源的重要组成部分。目前，我国风力发电初具规模，装机容量与日俱增。风力发电在迅速发展的同时，也伴随着巨大的挑战。风电机组内部结构相对比较复杂，工作环境比较恶劣，因此风电机组故障频发，发电可靠性能得不到保证，运维成本高。为了提高电力系统的稳定性，提高风电机组发电的可靠性，减少运维成本，目前很多学者致力于风电机组故障的研究［1-2］。现阶段的研究大都是针对齿轮箱故障判断寻求最优算法，例如改进灰色算法和时间序列法［3］，相关向量机和遗传算法结合［4］，改进的 Hilbert 变换包络解调法［5］，阶次 分析法［6］以及基于锦标赛选择策略的双种群人工蜂群算法［7］等，但是都存在一定的局限性。文献［8］提出了一种基于马尔科夫链并利用历史检查维护数据的齿轮箱轴承状态评估和剩余寿命预测方法，该方法降低了对大量监测数据的依赖性且不需要安装在线监测设备，但是准确率有待提高。文献［9］用人工免疫算法对BP神经网络进行改进，用于风机齿轮箱故障趋势的预测，以单位时间内的维护成本率最小为优化目标，同时在维护模型中考虑了维护和置换所用时间以及回复改善因子，进行优化求解，但是其优化目标较为单一具有局限性。文献［10］提出了一种基于随机子空间识别方法的齿轮箱故障预测算法，所提方法虽然能够预测出故障的发生，但在识别出具体故障方面还需要完善。

针对风机齿轮箱轴承故障诊断，提出了一种将离散粒子群优化算法 （Discrete Particle Swarm Optimization，DPSO）与基于多尺度小波核函数的核极限学习机 （Multi-scale Kernel Extreme Learning Machine，MKELM）相结合的新型DPSO-MKELM算法，并进行了实验分析，结果表明该算法具有更高的分类精度和较快的收敛速度。

1 改进型DPSO算法

1.1 粒子群算法原理

粒子群优化算法（Particle Swarm Optimization，PSO）起源于对鸟类捕食行为的研究，于1995年被Kennedy 和 Eberhart两位博士首次提出［11］。

PSO通过模拟鸟类捕食行为解决优化模型，通过食物位置确定优化模型的最优解，通过鸟群和食物的距离确定寻优的能力。PSO将鸟群的个体都看作是粒子，即潜在的解。每个粒子在多维空间飞行并且粒子的好坏由适应度函数决定。粒子在飞行过程中根据自身的飞行经验以及周围优质粒子的飞行特征，不断调整飞行状态，从而达到群体最优状态，最终找到的全局最优解［12］。该算法易于实现、收敛速度快、优化能力强，被广泛用于各种领域。

1.2 PSO的改进

1.2.1 改进权重因子

权重因子对PSO算法性能的影响很大。如果较大时，可以增强粒子全局搜索能力，有利于增加种群的多样性［13］；如果较小时，可以增强粒子局部搜索能力，有利于改善算法的收敛性。在传统PSO算法中，取在（0，1）之间［14］，不利于增加种群的多样性和改善算法的收敛性。因此，对权重因子的改进如下：

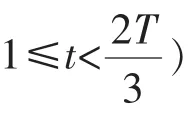
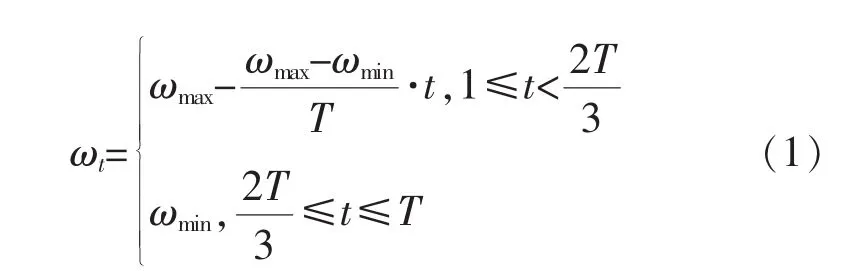
1.2.2 改进学习因子

学习因子c1和c2分别代表粒子的自我学习和社会学习，分别控制算法的全局搜索和局部搜索。使用动态学习因子 c1、c2，其中 c1和 c2之和不大于 4［15］。在算法搜索前期，设置的c1值大于c2值，粒子主要依靠自身的历史经验对全局进行搜索，避免陷入局部最优状态；在搜索后期，设置的值小于值，粒子主要依靠种群的优势信息进行搜索，最终粒子聚拢到全局最优区域。因此，对学习因子c1、c2的改进如下：

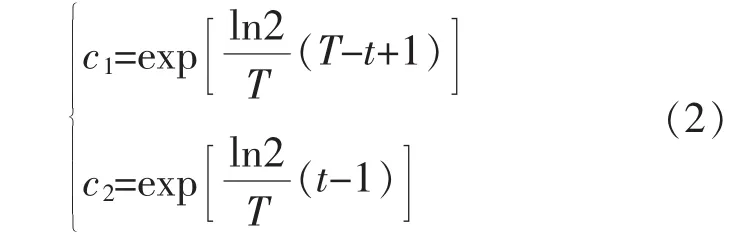
1.2.3 适应度函数

适应度函数是PSO算法的关键［16］，关系到算法的收敛速度，甚至对最优解的选取也有影响。使用的适应度函数如式（3）所示。

式中：K 是迭代次数；R（λ）为本次迭代值；R（0）为期望值。

2 多尺度小波核极限学习机

2.1 极限学习机

极限学习机（Extreme Learning Machine，ELM）是由Huang等人在2006年提出［17］，是一种新型的单隐层前馈神经网络。极限学习机相比于神经网络有泛化能力强、分类精度高、运算速度快等优点，由于运行过程无需迭代并且隐含层节点随机产生，能够避免结果容易陷入局部最优的缺陷［18］，被广泛应用于人工智能以及模式识别等领域。

2.2 核极限学习机

轴承故障诊断需要多层映射，即需要很多隐藏层节点，而传统的极限学习机只有单层映射，只有一个隐藏层，不能满足需求。因此，将核函数理论用于极限学习机构造核极限学习机KELM。每个样本的隐藏层输出可以看作是的线性映射，这种线性映射可以呈现ax+b或径向基函数 （Radial Basis Function，RBF）的形式。

因此，

根据核函数的理论，可以构造隐式映射来代替式（4）中的根据核函数的理论，可以构造隐式映射来代替式（4）中的内积，即构造核函数来替代HHT，具体步骤如下所示：

令 HHT（i，j）=K（xi，xj），则有

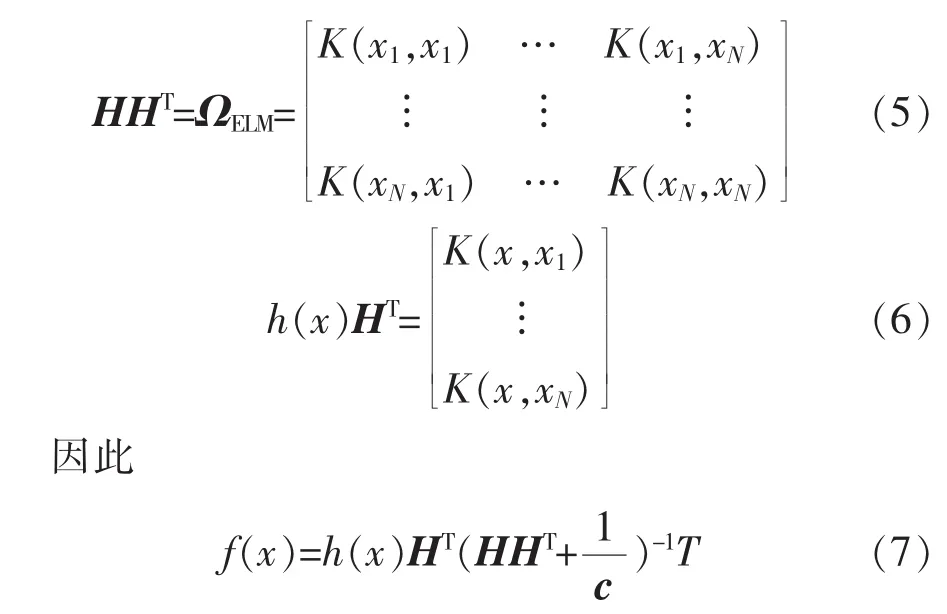
式中：c是正则化系数。

ELM解决方案的公式可以写成

相较于传统的极限学习机，改进后的核极限学习机具有更强大的函数逼近功能和次线性分类能力［19-20］。

2.3 改进型核极限学习机

与支持向量机（Support Vector Machine，SVM）类似，凡是满足Mercer条件的函数，都可以作为核极限学习机的核函数，例如Poly核函数、RBF核函数、Morlet核函数等。为了简化算法，将SVM内核应用于ELM。令母小波函数为h（x），其可伸缩性和平移因子分别为a和b，则小波基函数可表示为

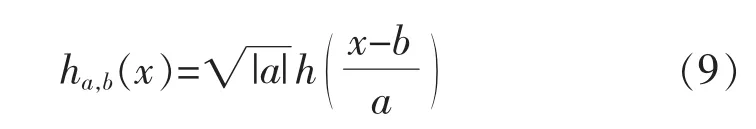
根据张量积理论，多维小波函数可以写成多个一维小波函数的张量积：

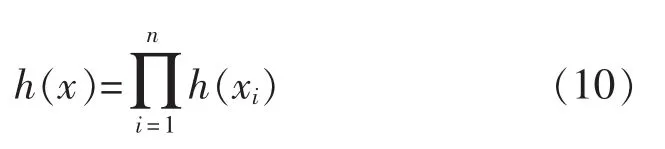
根据式（10），可以将核函数转化为

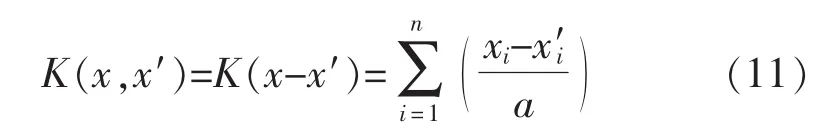
小波核函数具有非线性映射强的特点，可以高精度逼近任意函数。但在实际复杂的情况下，单一的小波核函数构造的核极限学习机不能满足应用需求，如数据异变或不规则，样本量较大，样品不均匀分布等。因此，可将多个不同尺度的小波核函数相叠加构成组合核函数。叠加形式如下所示。

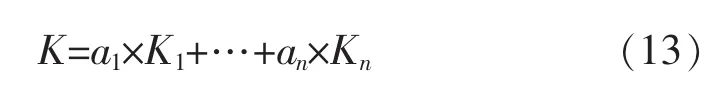
式（13）中尺度因子an主要作用是将不通尺度的小波核函数叠加，以获得拥有强大分类能力的组合核函数。多尺度小波核函数构造如下

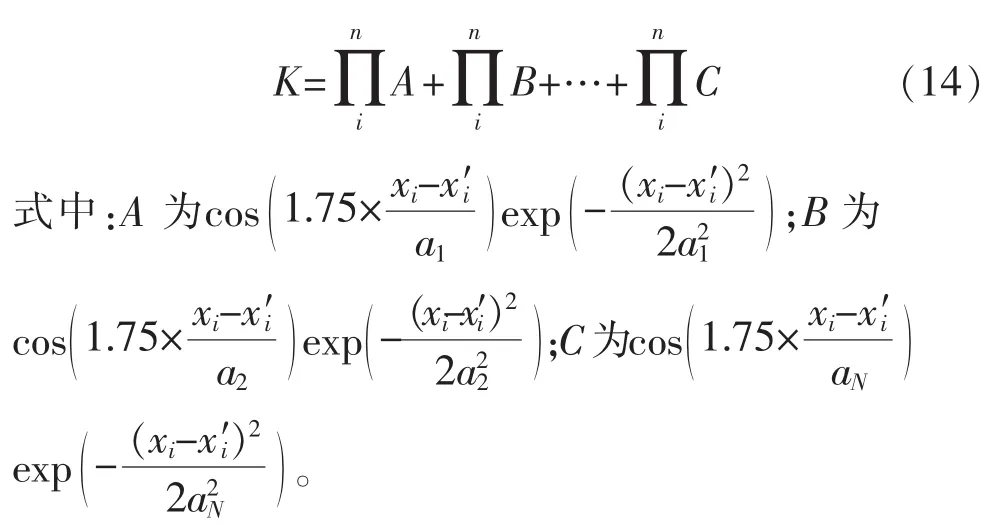
式（14）可以缩写为

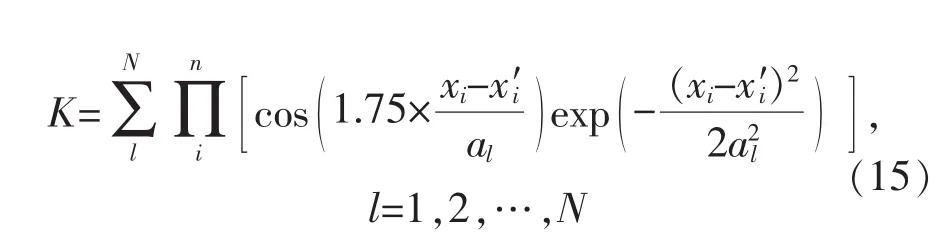
多尺度小波核极限学习机比单一的小波核极限学习机在参数选择方面范围更大，削弱了参数的影响，提高了识别效果，增强了逼近能力，使用更方便。

采用基于离散粒子群优化算法（DPSO）与核极限学习机（MKELM）的一种新型的DPSO-MKELM算法解决风机齿轮箱故障诊断，其流程如图1所示。

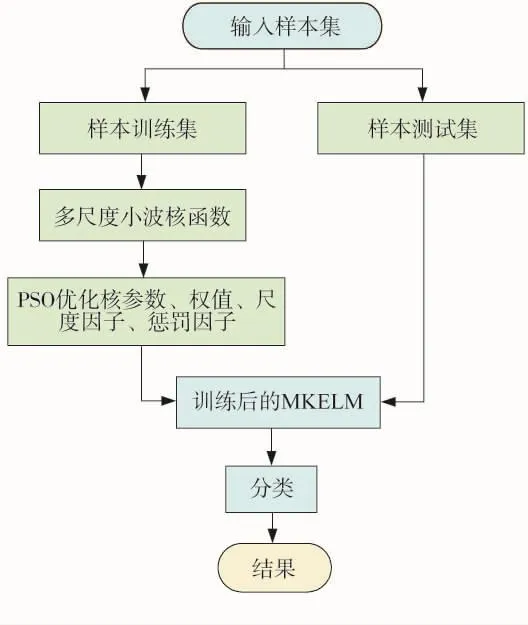
图1 PSO-MKELM模型流程

3 算例验证

针对某实际风电场故障部件轴承正常、轴承故障、保持架损坏等3种状态，采集振动信号，每种状态各采集60组数据。其中对每种状态各取50组数据用于训练PSO-MKELM模型，剩下30组用于测试误差，并与文献［21］中的高斯核函数的RPF-KELM以及传统的ELM算法进行了对比，结果如图2～4所示。图中“○”代表真实故障，“*”代表预测故障，只有两者重合时代表预测正确，不重合代表预测错误；故障类别数字1代表轴承正常，数字2代表轴承故障，数字3代表保持架损坏。

从图2～4可以看出，所提出的PSO-MKELM在3个故障识模型表现最突出，正确率达到96.667%。而文献［21］所提出的RBF-KELM模型识别正确率为93.333%，传统的ELM算法识别正确率只有90%，因此PSO-MKELM模型能够很好地完成轴承故障识别的任务。与此同时，多尺度核函数参数选择比单核函数参数选择更复杂，因此，多尺度小波核函数具有更好的泛化能力和更高的分类精度。

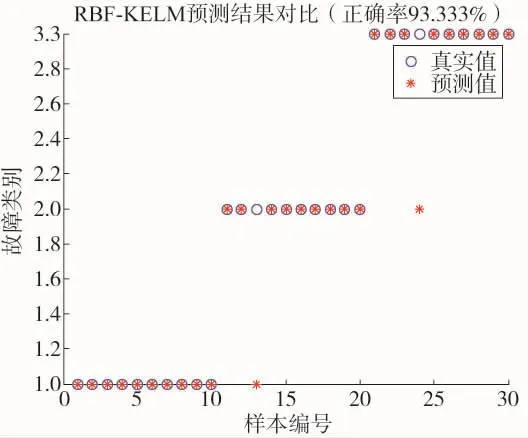
图2 RPF-KELM模型预测结果

图3 ELM模型预测结果

图4 DPSO-MKELM模型预测结果

4 结语

针对PSO算法的迭代过程中容易陷入局部最优状态，提出了一种改进型的DPSO算法。将满足Mercer条件的多尺度小波核函数作为极限学习机的核函数，并将其与DPSO结合，构建了DPSO-MKELM模型。在风轮机齿轮轴承故障诊断中的测试表明，多尺度小波核极限学习机在故障分类方面具有较高的精度，性能优于RPF-KELM和ELM，具有更高的应用价值。