基于买断模式下零售商的博弈分析
2019-07-03赵晨阳陈增
赵晨阳 陈增
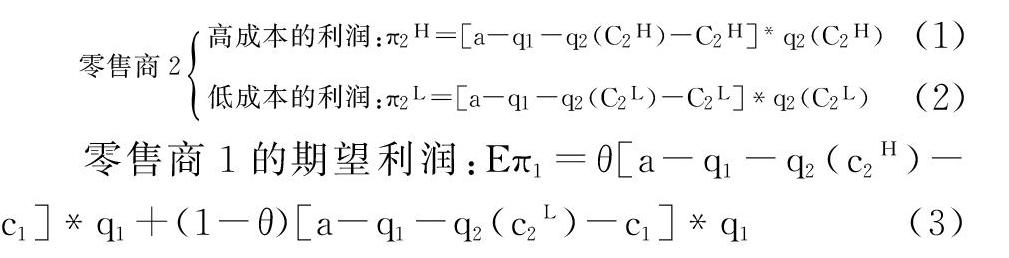

摘要:研究了由物流企业买断核心企业生产的产品后批发给多个零售商的买断模式,从博弈论的视角研究了在完全信息静态博弈与不完全信息静态博弈时零售商1 与零售商2的最优订购量决策问题。
关键词:买断模式; 博弈分析 ;最优订购量
中图分类号:F27文献标识码:Adoi:10.19311/j.cnki.1672-3198.2019.16.022
根据工信部中小企业司统计,截至2016年年末,全国规模以上中小工业企业达到37.0万,其中小微企业31.6万户,占比83.3%。中小工业企业主营业务收入大72.2万亿元占总工业企业的62.7%,同比增长6.0%,其中小微企业收入43.7万亿元,同比增长65%,中小工业企业提供就业岗位6140.6个,其中小微企业提供就业岗位3365.7万个,占比54.8%,由此可以看出中小企业不仅对经济的贡献巨大,对社会的贡献也是不容忽视。但融资难一直是制约中小企业进一步发展的重大难题。
1文献回顾
罗奇等人认为融通仓主要是以中小企业为服务对象并对其特点做了阐述。闫俊宏、许祥秦将供应链金融应用到中小企业,并分析了其应用优势。蒋婧梅、战明华分析了中小企业所特有的一些特点发现信息不透明、业绩不稳、缺乏抵押物是长期以来阻碍中小企业融资困难的最大障碍。曹文彬、马翠香从博弈论的视角引入违约罚数供应链金融应收账款可以达到帕累托最优,并且在提高放贷效率的同时降低风险和融资成本。陈斌通过对比物流金融和供应链金融的存货质押模式,发现供应链金融的存货质押模式使博弈各方达到帕累托最优。宋华、杨璇通过运用图论的方法研究了中小企业竞争力与网络嵌入度对供应金融的影响来解决中小企业融资难的问题。
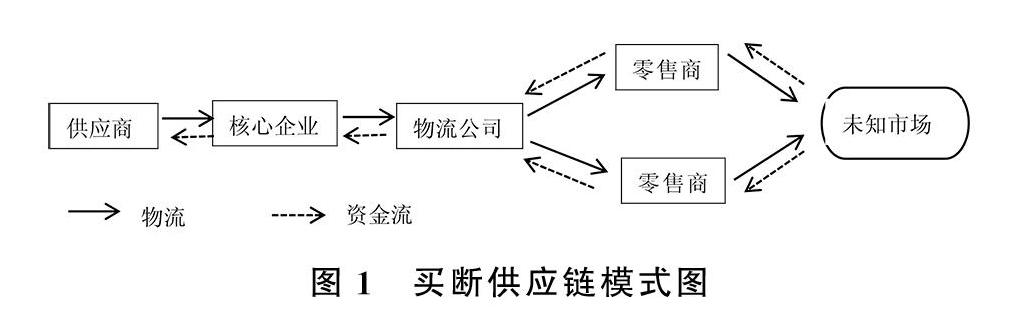
本文的研究在一定程度上为这些小微企业的决策提供了依据,具有一定的现实针对性,同时对于买断模式大多应用于金融市场诸如期货、债券,很少有人将买断模式与供应链相结合,因此在理论上也有一定的价值。所谓买断供应链模式就是指有物流企业买断核心企业生产出来的产品,获得产品的处置权后,根据自有仓库的位置就近匹配零售商,在由多个零售商将产品卖向市场,如图1所示。
2完全信息静态博弈
2.1基本假设
假设1:假设博弈主体为零售商1与零售商2二者均为理性人,并且两个人同时做出各自的订货量Q1与Q2,并以同样的价格p2卖给市场,市场中的产品提供者只有零售商1与零售商2,不存在其他的提供者。
假设2:物流公司以同样的批发价w批给零售商货物,并且规定零售商只有两种批发方案可选择一种是批发q1的货品,一种是q2的货品。且q1>q2。
假设3:零售商卖不出去的货品有物流公司回购,回购价格为p1,且p1 假设4:市场的需求量为x,市场好的概率为θ(一般不为0),则市场差的概率为1-θ,市场好时需求量x>2q1,市场差时,2q2 假设5:当两个零售商进货量相同时,各自占领1/2市场份额,当进货量不同时,进货量大的市场份额为2/3,进货量小的为1/3。 假设6:零售商的销售成本相同,且为共同知识,为了便于分析不妨c=0,由于成本相同,c的不同取值不会影响博弈结果。 2.2建立博弈模型 当Q1=Q2=q1时, 零售商1与零售商2的期望利润相同:Eπ1=π2=θ(p2-w)q1+(1-θ)[(q1-x/2)p1+p2x/2-wq1]=A; 当Q1=q2,Q2=q1时, 零售商1的期望利润:Eπ1=θ(p2-w)q2+(1-θ)[(q2-x/3)p1+p2x/3-wq2]=B 零售商2的期望利润:Eπ2=θ(p2-w)q1+(1-θ)[(q1-x2/3)p1+p2x2/3-wq1]=C; 当Q1=q1,Q2=q2时, 零售商1的期望利润:Eπ1=θ(p2-w)q1+(1-θ)[(q1-x2/3)p1+p2x2/3-wq1]=C 零售商2的期望利润:Eπ2=θ(p2-w)q2+(1-θ)[(q2-x/3)p1+p2x/3-wq2]=B 当Q1=Q2=q2时, 零售商1与零售商2的期望利润相同:Eπ1=Eπ2=(p2-w)q2=D。 因为A-C=θ(p2-w)q1+(1-θ)[(q1-x/2)p1+p2x/2-wq1]-θ(p2-w)q2-(1-θ)[(q1-x2/3)p1+p2x2/3-wq1] =(1-θ)[p1(q1-x/2-q1+x2/3-p2x(2/3-1/2)]=(1-θ)[1/6(P1-P2)],又因為q1>q2,所以A>C。 因为B-D= θ(p2-w)q2+(1-θ)[(q2-x/3)p1+p2x/3-wq2]-(p2-w)q2 =(1-θ)(w-p2)q2+(1-θ)[(q2-x/3)p1+p2x/3-wq2]=(1-θ)[(w-p2)q2+(q2-x/3)p1+p2x/3-wq2 =(1-θ)*(q2-x/3)(p1-p2),又q1>q2 ,所以当q2>x/3,B>D;当q2 故当A>C,q2>x/3即B>D,博弈如表1所示。 此时有唯一的纳什均衡,零售商1和零售商2的最优策略都是订q1的量才能获得最大收益。 当A>C,q2 此时有两个的纳什均衡,零售商1和零售商2的最优策略是保持相同的订货量才能获得最大收益。 3不完全信息静态博弈 3.1基本假设 假设1:逆需求函数的表达式为p(Q)=a-(q1+q2),其中Q为市场的总供给量,p为产品的市场价,q1、q2分别为零售商1与零售商2从物流企业的订购量。 假设2:假定零售商1的销售成本为c1(q1),为共同知识,零售商2由于采用了新的销售技巧线上线下结合销售,其销售成本为c2(q2),由于c2属于零售商2的私有信息,零售商1并不知道零售商2的真实成本,只知道零售商2的成本可能是c2L(低成本),也有可能是c2H(高成本),并且认为是c2H的概率为θ,是c2L的概率为1-θ,并且c2H>c2L,但零售商2知道自己真实的成本。 假设3:市场中只有零售商1与零售商2提供这种产品,并且二者均为理性人。 3.2建立博弈模型 零售商2高成本的利润:π2H=[a-q1-q2(C2H)-C2H]*q2(C2H)(1) 低成本的利润:π2L=[a-q1-q2(C2L)-C2L]*q2(C2L)(2) 零售商1的期望利润:Eπ1=θ[a-q1-q2(c2H)-c1]*q1+(1-θ)[a-q1-q2(c2L)-c1]*q1(3) 对(1)式的q2(c2H)求导,使其等于零,可以等到零售商2在高成本時的最优订购量,同理对(2)、(3)式求导使其为零,分别得到零售商2在低成本时的最优的订购量,以及零售商1在知道零售商2上高成本的概率但并不知道具体是高成本还是低成本时自己的最有订购量。 4结论 在完全信息静态博弈中当物流企业只提供两种订货方案时当A>C,q2 参考文献 [1]罗齐,朱道立,陈伯铭.第三方物流服务创新:融通仓及其运作模式初探[J].中国流通经济,2002,(2):11-14. [2]闫俊宏,许祥泰.基于供应链金融的中小企业融资模式分析[J].上海金融,2007,(2):14-16. [3]蒋婧梅,战明华.中小企业供应链金融研究综述[J].经营与管理,2012,(11):115-116. [4]曹文彬,马翠香.基于供应链金融的应收账款融资博弈分析[J].商业研究,2013,24(2):14-21. [5]陈斌.我国中小企业存货质押融资模式的博弈分析[J].莆田学院学报,2013,20(5):14-21. [6]宋华,杨璇.中小企业竞争力与网络嵌入性对供应链金融绩效的影响研究[J].管理学报,2018,(4):616-624.
