带鼓包的背负式大S弯进气道流场特性及参数影响规律
2019-07-03贾洪印周桂宇唐静吴晓军马明生
贾洪印, 周桂宇, 唐静, 吴晓军, 马明生
(中国空气动力研究与发展中心 计算空气动力研究所, 四川 绵阳 621000)
进气道作为推进系统的重要组成部分,其性能的优越将直接影响战斗机的性能。对于高隐身需求的作战飞机,进气道系统的雷达散射面积能否有效控制直接影响飞机的隐身性能[1]。为降低飞机进气系统的雷达散射面积,进气道布局形式上可采用背负式设计,同时,为实现对发动机进口端面的有效遮挡,可采用紧凑的蛇形大S弯内管道形式[2]。这种高隐身的进气道系统设计近些年来受到了越来越多飞行器设计者的青睐[3],如美国的“B2”、“X-47”等飞行器就采用了背负式进气道布局结合大S弯内管道的设计方案。然而,背负式进气道布局自身有一定缺陷[4],在较大迎角时不能很好利用高能来流的冲压,在设计时需充分考虑机身、机翼、进气道唇口等部件对进气道性能的干扰影响。紧凑式大S弯内管道设计容易造成流动分离,使得总压恢复系数降低,流场畸变增大,降低进气道性能[5]。
在背负式进气道、无附面层隔板进气道(DSI)研究方面,罗普格鲁门公司的Williams等[6]通过试验方法对背负式进气道进行了大量研究,指出背负式进气道的性能与飞机布局细节密切相关,必须与机体进行一体化综合设计。同时,通过对后掠的三角翼外形的研究发现,边条漩涡对背部进气口的低能量气流起到有利的“扫除”作用,可以提高大迎角时总压恢复和降低畸变。波音公司Richard[7]对军用飞机超声速进气道系统进行了详细介绍,分析了F35采用的机身两侧DSI进气系统入口波系和鼓包对附面层排除机理;洛克希德马丁公司的Hamstra等[8],采用先进的鼓包修型技术,提升了DSI进气道附面层排除能力;Kim等[9]将传统进气道压缩面置换为三维鼓包,通过优化鼓包长度和高度,提升了进气道的总压恢复,降低了进气道出口畸变。Tan和Guo等[10]将背负式进气道方案与无附面层隔板技术进行了结合,研究了鼓包高度对DSI进气道性能的影响。国内在背负式大S弯进气道设计及分离流动控制方面也开展了大量的研究工作。南京航空航天大学张航和谭慧俊等[11]对安装在背部的类X-47狭缝式进气道进行了设计和仿真,获得了该类进气道的流动特征和工作特性。北京航空航天大学李大伟等[12]针对无人机特点,设计了一种短扩压、大偏距、背负式S形进气道,并通过仿真的方法,分析了进气道出口流场图谱和机身对进气道性能的影响。
在大S弯进气道性能预测方面,AIAA从2012年至今共组织召开了4届推进空气动力学研讨会[13-15],针对设计的大S弯进气道研究标模,考核现有CFD代码、网格和湍流模型在大S弯进气道内分离流动预测的可靠性,给出CFD模拟的指导原则。来自NASA、波音、DLR等空气动力学研究机构采用自主开发的CFD代码,系统研究了不同网格、不同湍流模型、不同来流速度对大S弯进气道内流动的影响。
从目前公开发表的文献来看,国内相关方面的研究大多集中在对背负式进气道[4]、DSI进气道[16]、大S弯进气道流动特性和进气道内流动控制技术的研究[17],而针对背负式进气道布局、带大S弯扩散段的DSI进气道一体化研究开展还相对较少。
本文以带鼓包的背负式大S弯进气道为研究对象,采用非结构混合网格并结合自适应技术,通过数值求解NS方程,对超声速来流条件下的进气道流场特性及参数影响规律进行了一体化数值模拟研究。通过M2192大S弯进气道模型,验证了程序对进气道内分离流动预测的可靠性。在此基础上,对带鼓包背负式大S弯进气道在超声速来流情况下入口激波分布、进气道内部流动情况以及出口流场的气流品质进行了分析,重点考察了进气道入口鼓包高度、唇缘后掠角等几何参数对进气道性能的影响,得到了影响规律,可以为我国类似带鼓包背负式大S弯进气道设计提供参考。
1 数值方法
本文研究采用中国空气动力研究与发展中心自主开发的大规模并行流场解算器MFlow进行计算。该解算器支持任意形状的网格单元,方便对复杂流场区域进行自适应加密,变量存储于单元体心,控制方程采用有限体积方法进行离散,时间离散采用隐式的LU-SGS方法,空间离散集成了目前国际主流的空间离散格式和梯度求解方法,湍流模拟可采用SA一方程和SST两方程湍流模型,为了加速流场收敛,软件采用了FAS融合的多重网格方法、局部时间步长方法和基于MPI的大规模并行技术。目前,该软件多次参加AIAA组织的阻力预测和高升力预测会议,数据对比中取得了较好的数值模拟结果[18-19]。
在本文的研究中,采用四面体和三棱柱单元混合的非结构网格,并结合了网格自适应技术,对进气道入口激波位置进行了精细捕捉。主控方程对流项采用二阶迎风Roe通量差分裂格式进行离散,时间项采用隐式LU-SGS推进求解,梯度求解采用节点型Gauss方法,限制器采用Venkatakrishnan限制器,湍流模型采用SA一方程湍流模型和SST两方程湍流模型。
1.1 控制方程
控制方程采用守恒形式的非定常可压缩NS方程
(1)
式中,Ω表示控制体的体积,∂Ω表示控制体封闭面的面积,W为守恒变量,Fc为无黏通量,Fv为黏性通量。
1.2 网格自适应技术
网格自适应技术的目的是使用尽量小的网格量获得尽量高的计算精度,基本的思想是增加局部区域的网格分辨率,以便更好地捕捉流场细节,使计算的精度增加。网格自适应技术常用于含有激波或漩涡的流场,可以得到更精细的激波和漩涡结构。自适应探测器和网格细分策略是自适应技术的2个关键技术。梯度探测器和法向马赫数探测器可以有效地确定激波的位置,熵增探测器可以确定涡核及附近区域,不同探测器的定义式如下:
法向马赫数探测器[20]
(2)
熵增探测器[21]
(3)
1.3 湍流模型
大S弯进气道内通常存在较强的逆压梯度和黏性相互作用,产生复杂的流动分离现象,对湍流模型要求较高。本文研究采用工程上应用广泛且相对成熟的2个湍流模型,SA一方程模型和SST k-ω两方程湍流模型。
将湍流方程写为如下统一的守恒积分形式
(4)
SA一方程湍流模型公式的各部分及系数定义参见文献[22],SST k-ω两方程湍流模型公式各部分及系数定义参见文献[23]。
本文中湍流模型方程的求解采用与主流控制方程解耦的方式进行,这样一方面可以减少对主流控制方程的求解难度;另一方面可以很好地利用已有的层流流场解算器,从而减少编程工作量;最重要的是可以减少计算量,提高计算效率,因为解耦避免了求解高阶矩阵。
2 方法验证
为了验证本文采用的数值计算方法在进气道内流计算中的可靠性,我们选取了RAE M2129大S弯进气道模型对程序进行了考核验证。该进气道模型是在NASA和UK Ministry of Defense的支持下,在DRA/Bedford 13x9英尺风洞进行了风洞试验,并被广泛应用于CFD程序验证与确认[24]。
图1给出了该进气道外形的网格分布,计算采用三棱柱和四面体混合的网格单元。网格单元总数约为617万,其中四面体单元160万,三棱柱单元457万,附面层第一层间距按y+=1选取,物面法向三棱柱网格单元数为35。为了验证程序可靠性,共计算了2个不同流量条件下进气道性能,对应进出口气流压力比分别为0.950 78和0.747 63,来流马赫数M为0.21,攻角α为0°,雷诺数为0.388 5×106。
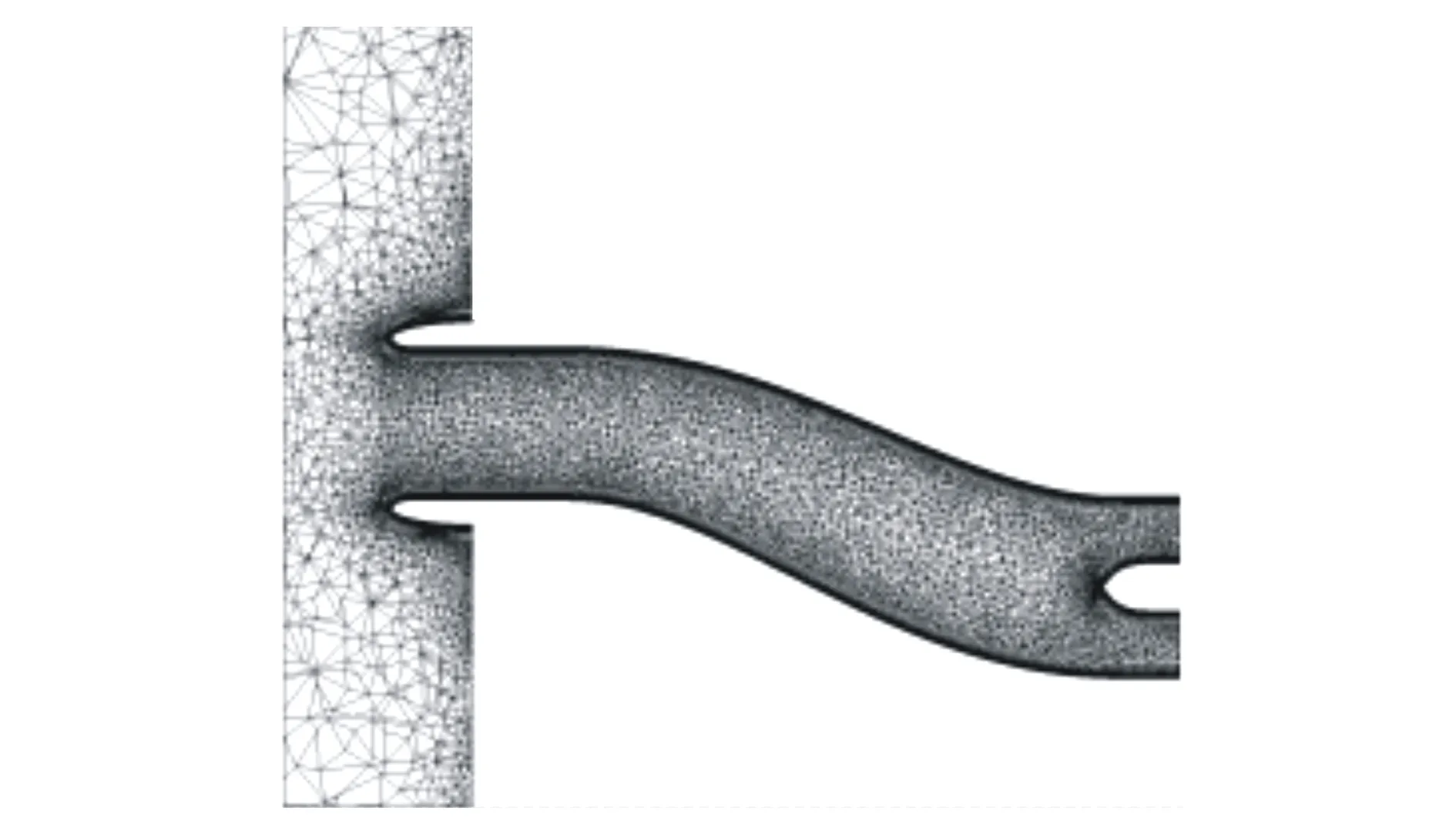
图1 M2129进气道模型网格分布
图2分别给出了采用2种不同湍流模型计算得到的进气道上下壁面压力分布与试验值的对比情况。可以看出,在不同流量条件下,SA和SST湍流模型计算得到的下表面分离位置较试验比均略靠前,但整体来说,计算与试验得到的压力分布均吻合较好,说明程序可以捕捉到大S弯进气道内部典型流动特征。表1给出了采用不同湍流模型计算得到的进气道出口的总压恢复系数与试验值及文献值的对比情况,可以看出,本文计算得到的总压恢复系数与试验及文献值吻合较好,尤其是在小流量系数条件下,与试验值差别不到1%,说明本文采用的数值计算方法可以用于大S弯进气道性能分析,验证了程序的可靠性。
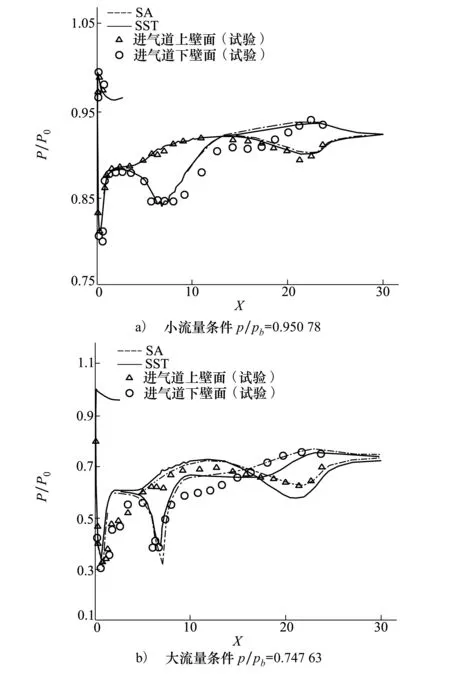
图2 计算与试验进气道上下壁面压力对比
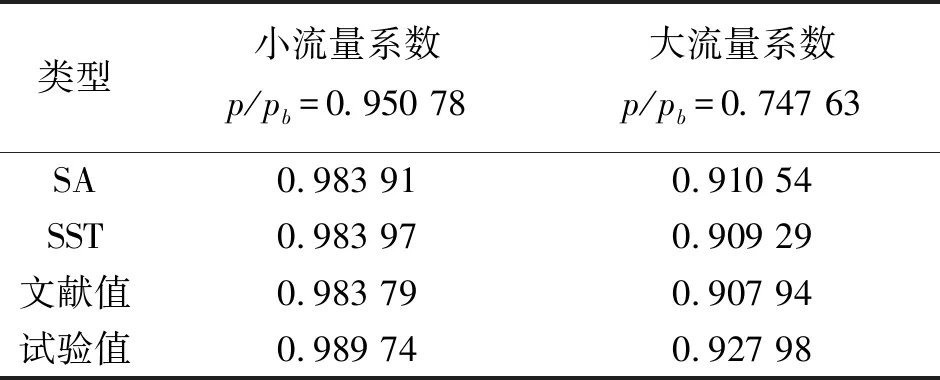
类型小流量系数p/pb=0.950 78大流量系数p/pb=0.747 63SA0.983 910.910 54SST0.983 970.909 29文献值0.983 790.907 94试验值0.989 740.927 98
3 计算结果讨论分析
本节利用前面介绍的数值计算方法,对某带鼓包的背负式大S弯进气道在超声速来流条件下的流场特性及参数影响规律进行了一体化数值模拟研究。该进气道内管道采用双大S弯曲设计,唇口为后掠形状,无附面层隔道,在进气口处采用鼓包设计,这个鼓包起到对来流的压缩作用,并产生一个把附面层气流推离进气道的压力分布。为了较好地对流场特性进行捕捉,数值模拟分析时采用了网格自适应技术,提升局部流场特性捕捉精度。图3给出了自适应前后进气道入口附近网格分布。可以看出,网格自适应后进气道鼓包处的压缩激波模拟的更加精细。

图3 背负式进气道自适应前后网格分布
3.1 进气道超声速流场特性分析
图4给出了该背负式进气道在超声速M为1.53情况下计算得到的进气道总压恢复系数与试验值对比曲线,其中横坐标为流量系数,纵坐标为总压恢复系数,可以看出,计算得到的总压恢复系数与试验值吻合较好,随着流量系数的逐渐增大,进气道出口总压恢复逐渐降低,总压损失严重。图5给出了不同流量系数条件下出口截面上总压分布,可以看出,随着流量系数的增大,总压分布变得越来越不均匀。

图4 计算与试验总压恢复系数对比

图5 不同流量系数对应出口截面的总压分布
图6给出了在流量系数为0.6时进气道入口附近马赫数分布云图,可以看出,机头产生第一道斜激波后,鼓包压缩产生锥型波,系列锥形波经鼓包压缩后形成末激波。在末激波后面,气流变成亚声速,进入进气道内。在进气道外唇口附近,在该流量系数下进气道产生溢流,使得唇口外表面气流加速,局部变成了超声速。随着进气道流量的增大,进气口处的末激波会逐渐发生内移,造成总压损失逐渐加大,进气道性能下降。
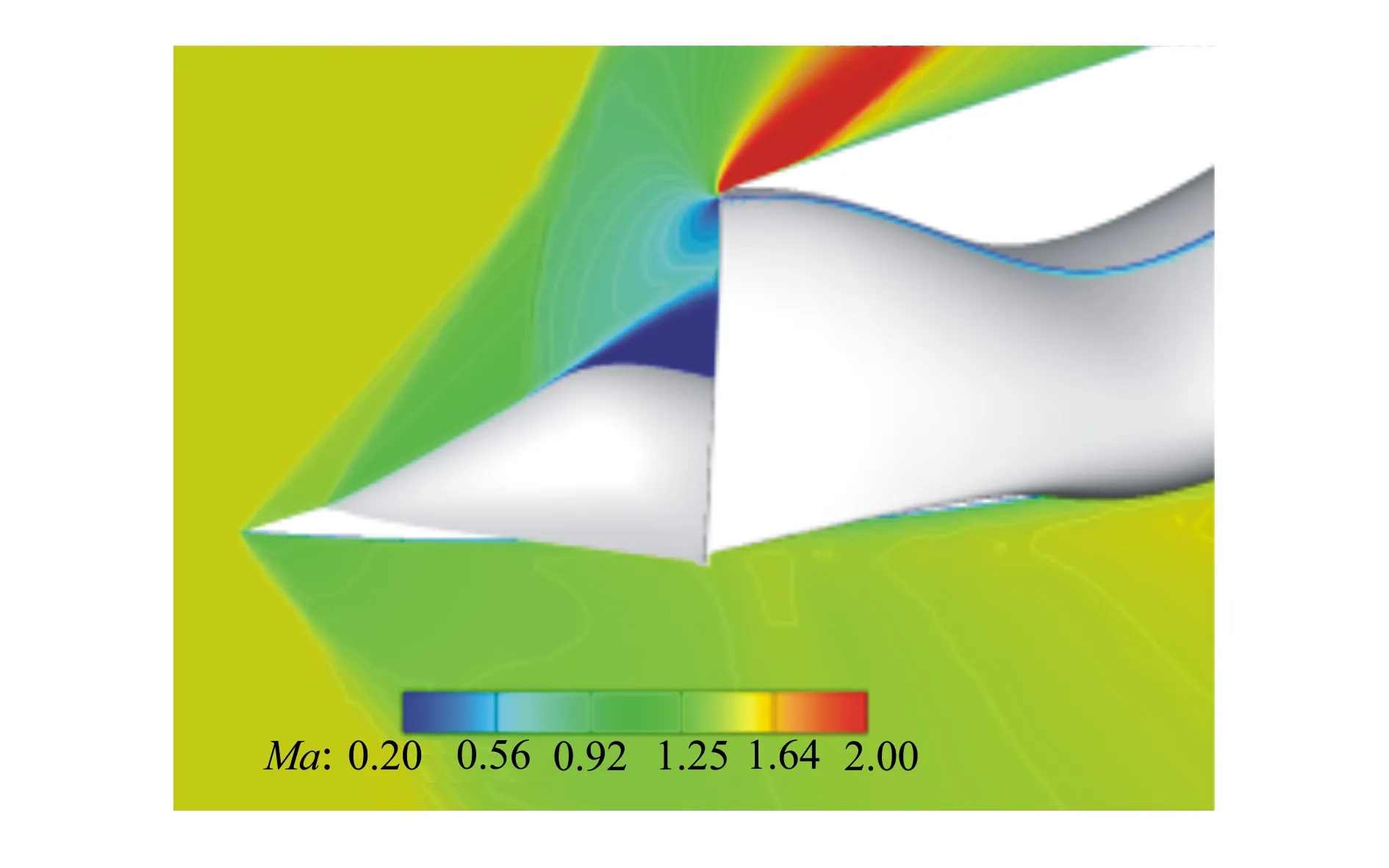
图6 进气道入口附近马赫数分布云图
图7给出了进气道内不同截面的总压分布和空间流线分布。可以看出,气流在经过鼓包以后在进气道的下壁面发生了分离,形成了一个较低动量的区域,随着流动不断向下游传播发展。气流在S弯管道内部,由于在转弯位置曲壁顶部压强大于底部压强,在附面层内,速度低于核心流,为了平衡径向压强梯度,需要附面层内速度较低的气流向内转折一个更大的角度,从而出现由顶部到底部的横向流动,形成二次流。同时,我们可以发现,气流在经过第二道S弯时,由于曲壁产生的压力梯度改变符号,使得下壁面附近的低能量区域有向顶部移动的趋势。图8分别给出了流量系数在0.6和0.77情况下进气道出口截面速度矢量分布,图中云图采用马赫数着色。可以看出,随着流量系数的不同,出口截面的二次流的形态会有所差别,在小流量时,呈现的是一对反方向旋转的漩涡结构,而在大流量时,进气道出口截面会出现3对涡的结构。

图7 进气道内不同剖面总压及空间流线分布

图8 不同流量系数对应出口截面速度矢量图
3.2 鼓包高度对进气道性能影响
对于带鼓包的背负式大S弯进气道,影响其性能的参数较多,由于本文研究的进气道采用鼓包+后掠唇口的设计,不同的鼓包几何参数会对进气道的性能产生一定的影响,本节主要考察进气道入口处不同鼓包高度对进气道性能的影响。选取了3个高度A、B、C,具体外形示意图如图9所示。

图9 不同鼓包高度示意图
图10给出了不同鼓包高度对进气道性能影响规律曲线,可以看出,随着鼓包高度的增大,进气道的总压恢复系数逐渐降低。为分析其原因,图11给出了流量系数为0.6,鼓包A和鼓包C2种情况下进气道入口处的激波分布。结果显示,随着鼓包高度的增加,鼓包处的压力等值线发生后移,在鼓包后面越容易发生分离。图12给出了鼓包A高度下进气道内不同剖面的总压云图和空间流线分布,与图7鼓包C高度下进气道内不同剖面总压云图对比可以看出,随着鼓包高度的升高,鼓包后的低能量分离区逐渐变大,在来流和S弯曲壁的逆压梯度共同作用下逐渐向下游发展,从而导致进气道性能逐渐下降,总压恢复系数逐渐降低。
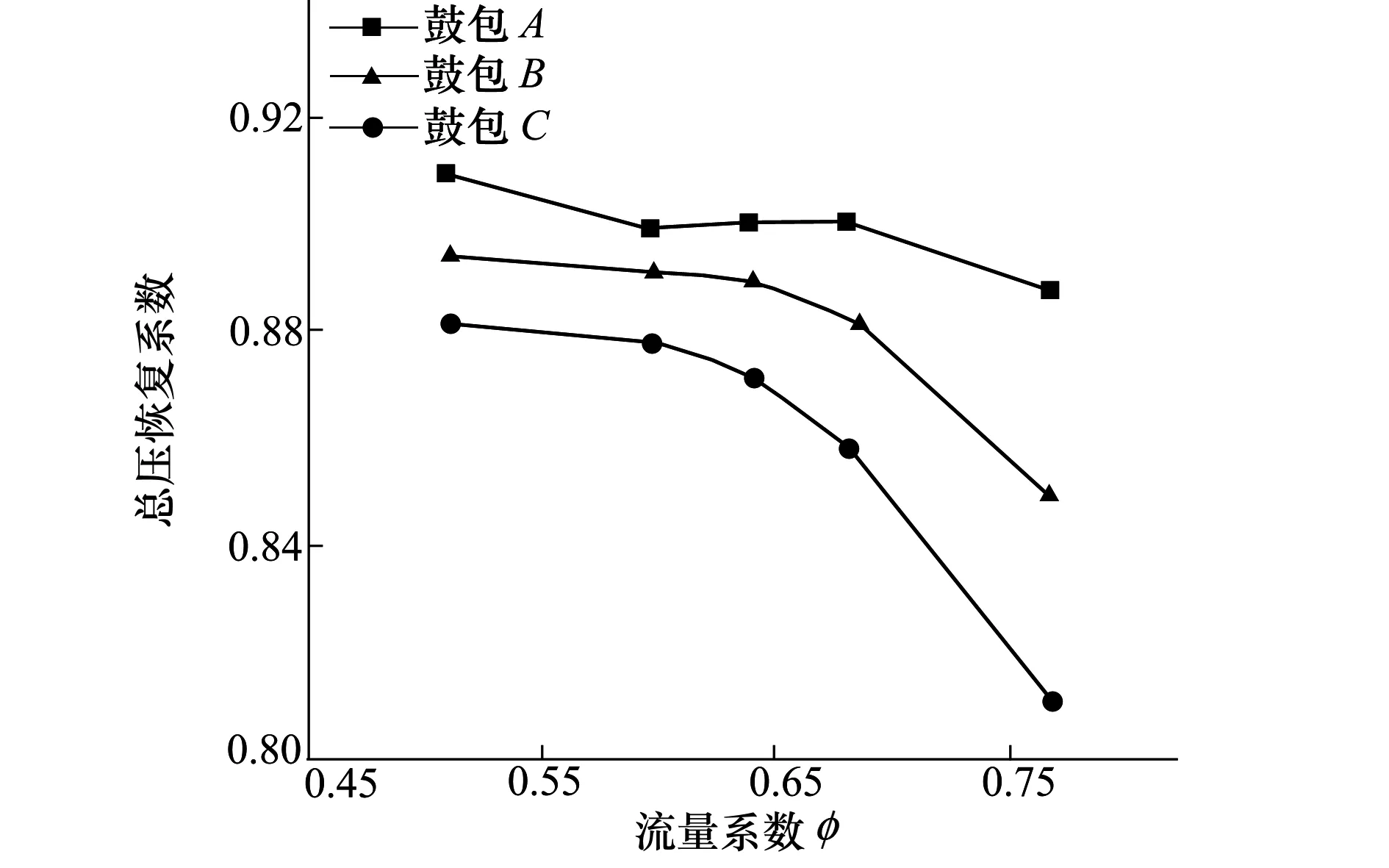
图10 不同鼓包高度对进气道性能影响曲线
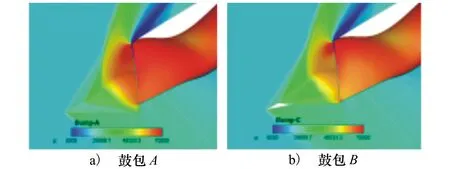
图11 不同鼓包高度对进气道入口附近波系影响
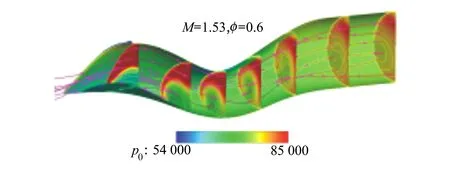
图12 鼓包A高度下进气道内总压和空间流线分布
3.3 唇缘后掠角对进气道性能影响
对于背负式进气道,不同的外流条件会对进气道入口处的气流产生较大的影响,从而影响进气道的性能。本节主要考察进气道不同唇缘后掠角对其性能的影响,我们选取了3个唇缘后掠角(35°,40°,45°)进行了计算分析,图13给出了不同唇缘后掠角的外形对比示意图。图14给出了不同唇缘后掠角对进气道性能影响的规律曲线,可以看出,随着后掠角的增大,进气道出口截面的总压恢复系数逐渐降低,为分析其原因,图15给出了唇缘后掠角为35°和45°情况下的进气道对称面压力分布,可以看出,进气道唇口位于末激波后面,处于亚声速区域,随着后掠角的增大,进气道内的压力逐渐降低,唇口位置产生的高压区位置逐渐后移,从而影响了进气道的入口气流,导致进气道总压恢复系数逐渐降低。
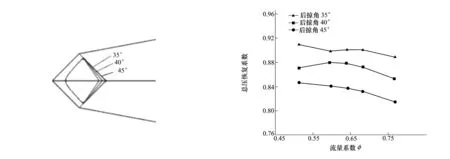
图13 不同唇缘后掠角示意图 图14 不同唇后掠角对进气道性能影响曲线
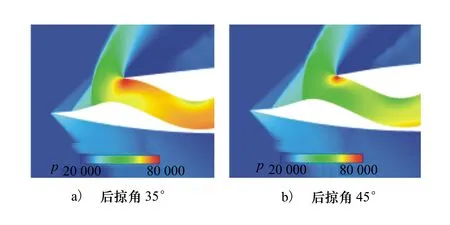
图15 不同唇缘后掠角对称面压力分布云图对比
4 结 论
本文通过对带鼓包的背负式大S弯进气道流场特性及参数影响规律的一体化数值模拟研究,可以得到以下结论:
1) 不同湍流模型对大S弯进气道出口总压恢复系数预测影响较小,SA和SST湍流模型计算得到的S弯管道下表面分离位置较试验比均略靠前,计算得到的S弯管道内压力分布和出口总压恢复系数均与试验值吻合较好,说明本文采用的数值计算方法可用于大S弯进气道内外流一体化性能分析。
2) 对于带鼓包的背负式大S弯进气道,在超声速时来流时,进气道入口处鼓包压缩产生锥形波,系列锥形波不断压缩,起到附面层排除的作用;鼓包后形成的低动量区域随着流动不断向下游发展,在弯曲管道曲率和压力梯度共同作用下,产生二次流动,流量系数不同,进气道出口截面的二次流形态差异较大。
3) 分析了不同鼓包高度、唇缘后掠角对进气道性能影响规律,结果表明,在一定范围内,适当降低鼓包高度或减小唇缘后掠角,有利于进气道性能改善。
