生丝纤度序列特征参数调查

林 祥，金振宇，朱恩松，殷 缘，薛坤仑，许建梅

(苏州大学 纺织与服装工程学院，江苏 苏州 215021)

生丝是桑蚕茧缫丝后所得到的产品，日本近代的缫丝产业一度迅猛发展，20世纪初占到美国市场份额达80%[1]；如今中国作为世界最大的生丝生产国，在国际生丝贸易中也一直位居世界首位。在生丝贸易中为了对生丝质量进行评价，通常需要进行生丝检验。1956年中国第一版生丝标准中首次规定了生丝纤度偏差、纤度最大偏差[2]。但是随着科技进步，缫丝设备与缫丝技术都大大进步，生丝品质也提高很多。原有的检验方法与标准显得相对落后，所以现在国际与国内正大力推广生丝电子检测技术，相应的电子检测方法分级标准也正在研制中[3]。对生丝电子检测方法分级标准研究时则需要大量的检测数据，而通过实际检测获取大量数据的方法费时费力，因此采用计算机模拟实验生成任意长度的生丝纤度曲线，来对其进行理论分析，模拟生丝检验是一种较好的方法。在模拟生丝纤度曲线时，白伦[4-5]建立了生丝纤度自相关系数模型来描述生丝纤度序列的数据之间的相关性与周期变化特性。所以在进行生丝纤度曲线的计算机模拟研究之前，需要了解生丝纤度曲线的特征参数。

前人对于生丝纤度曲线的特征参数的调查与获取方法做了很多研究，如对于生丝纤度时间序列，白伦[6]在假定其自相关系数可用衰减振动模型描述的条件下，利用谱密度函数给出拟似周期及衰减率的推定方法，建立数据模型讨论了其实际应用问题；罗军[7]将自相关系数理论模型看成等周期的，对理论模型进行了参数估计。十几年前，生丝的主要生产方式是采用定粒缫丝，当时的纤度研究与调查也是基于定粒缫生丝，而如今定纤缫丝完全代替了定粒缫丝，同时随着现代缫丝技术的发展，生丝的质量也发生了很大的变化。因此有必要重新对生丝纤度序列的特征参数进行调查。

为此，本文采用测长称重法来获得生丝纤度序列，利用自相关系数模型计算出反映生丝纤度序列数据之间相关性与周期性的特征参数，经移动平均得到修正后的生丝纤度序列特征参数，研究结果希望为生丝纤度研究中进一步的模拟实验提供当前生丝纤度质量的特征参数取值。

1 生丝纤度序列特征参数及估算方法

1.1 生丝纤度自相关系数序列

时间序列即为对于一个动态的变化过程，按照一定的时间间隔进行观察，用一个有序的数列形式表达的结果。在本文的研究中，通过测长称重法称得生丝纤度的时间序列后，可根据下式计算出生丝纤度的自相关系数并绘制纤度曲线。

(1)

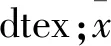
1.2 生丝纤度自相关系数序列模型

生丝纤度序列的自相关系数反映的是数据之间的关联性与周期性，为此，白伦[6]建立了如下式所示的统一的自相关系数模型，用来描述各种类型的自相关系数波动情况。

(2)

式中：参数λ称为衰减率，T为拟似周期，表达了纤度波动变化的周期。

不论定粒缫丝还是定纤缫丝，其纤度波动特性都可以用这个模型来表示。也就是说对于一定的生丝纤度均值和方差，调整λ和T值时，理论上自相关系数模型可以相当真实地描述不同原料茧特征与缫丝条件下的纤度连续变动特征。

1.3 生丝纤度序列特征参数估算

取自相关系数序列的一些特征点比如其波谷与波峰值作为估算点来计算衰减率与拟似周期。假定选取(k1,ρk1),(k2,ρk2),…(kn,ρkn)等波峰点作为特征点，那么其拟似周期则可根据下式来进行计算：

(3)

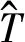
衰减率λ则可通过下式计算：

(4)

1.4 特征参数估计的修正

当前定粒缫生丝基本淘汰，主要是定纤生丝[8]。定纤生丝的周期性变化不如定粒生丝明显，因此用实测得到的纤度序列数据，计算出的生丝自相关系数曲线与自相关系数模型差异较大，部分曲线存在诸多微小波动，曲线不规则，难以观察准确的周期变化，存在拟似周期选择不准确、特征参数误差大等缺陷[9]。对于这部分曲线可以采取扩大检验丝长的方法来减少或消除数据列当中较小的波动，以更好地选取拟似周期点。通过将相邻的几个纤度值求平均，即可得到新的纤度序列。如果是每两个数值求平均，则相当于检验丝长扩大两倍，如果是每三个求平均，则是扩大三倍，如此类推，直至得到的新的序列周期明显易于计算为止。

2 实 验

2.1 材料与仪器

材料：22.2/24.4 dtex(20/22 D)，32.2/34.4 dtex(29/31 D)，44.4/48.9 dtex(40/44 D)三种规格样丝(苏州苏豪生物技术有限公司)。

仪器：附有回转计数器和自停装置的纤度机(无锡第二纺织机械厂)，最小分度值为0.1mg的赛多利斯BS210S电子天平(苏州赛恩斯仪器有限公司)。

2.2 步 骤

本文采用测长称重法来获得生丝纤度序列，长度间隔设置为8 m。对短片段生丝纤度序列进行调查，选取三种规格生丝，每种规格生丝选取若干个卷装，检验丝长为8 m。每个卷装(抱平)生丝被切成等长度片段序列并称重，顺序记录，这样即可得到各种规格生丝的多个生丝纤度序列[10]。

3 结果与分析

3.1 生丝纤度序列

实验共对三种规格生丝进行了检测，其中22.2/24.4 dtex规格生丝选测了10个样本，32.2/34.4 dtex规格6个，44.4/48.9 dtex规格8个。图1是各规格随机选取的两个样本的纤度曲线。

a1，a2为22.2/24.4 dtex规格4号、7号样本；b1，b2为32.2/34.4 dtex规格2号、3号样本；c1、c2为44.4/48.9 dtex规格4号、5号样本图1 三种规格样品生丝纤度序列曲线Fig.1 Raw silk size series curves of silk samples of three specifications

从图1可以看出，22.2/24.4 dtex规格4号与7号样本纤度曲线具有周期性，样本数据存在从小到大渐变再从大到小渐变的规律，纤度数值基本围绕23.3 dtex上下浮动，7号生丝波动较大。32.2/34.4 dtex规格2号与3号样品生丝纤度起伏不大，除去波峰和波谷值，基本在33.3 dtex上下浮动变化；44.4/48.9 dtex规格4号样本生丝纤度基本在46～48 dtex内波动，4号样本纤度变化与5号相比较大，有较多峰值和谷值，呈锯齿状，无明显规律。

3.2 三种规格生丝自相关系数分析

利用生丝纤度数据，由式(1)计算后得到其分别对应的样本纤度自相关系数图，图2即为图1中所显示的生丝纤度序列计算得到的自相关系数序列。由22.2/24.4 dtex规格4号样品可以看出，生丝的自相关系数具有明显的波峰波谷，可以初步看出其变化周期，7号样规律性稍差；32.2/34.4 dtex规格样品生丝自相关系数曲线整体呈现下降趋势，周期不易观察。44.4/48.9 dtex生丝自相关系数曲线均较为杂乱，周期性偏小。这是因随着纤度增加同一绪头的绪下茧数量增加，在相同的解舒丝长条件下，同样长度的生丝，自然落绪引起的茧丝切断次数增加，纤度变动周期变短，而同时由于茧丝由细到粗再到细的天然变化特性，导致切断次数增加时纤度变化的周期性减弱。

3.3 参数估计

根据各种规格生丝自相关系数数据，运用式(3)和式(4)中的估算方法计算序列的拟似周期与衰减率，计算结果如表1所示。

由表1估算结果来看，22.2/24.4 dtex规格生丝拟似周期在168～208 m，32.2/34.4 dtex规格生丝拟似周期均值在124～197 m；44.4/48.9 dtex规格的生丝在58～144 m。λ的值则随T和峰值的变化而变化，随着T值的增大逐渐减小。

图2 三种规格生丝纤度自相关系数曲线Fig.2 Autocorrelation coefficient curves of raw silk size of three specifications

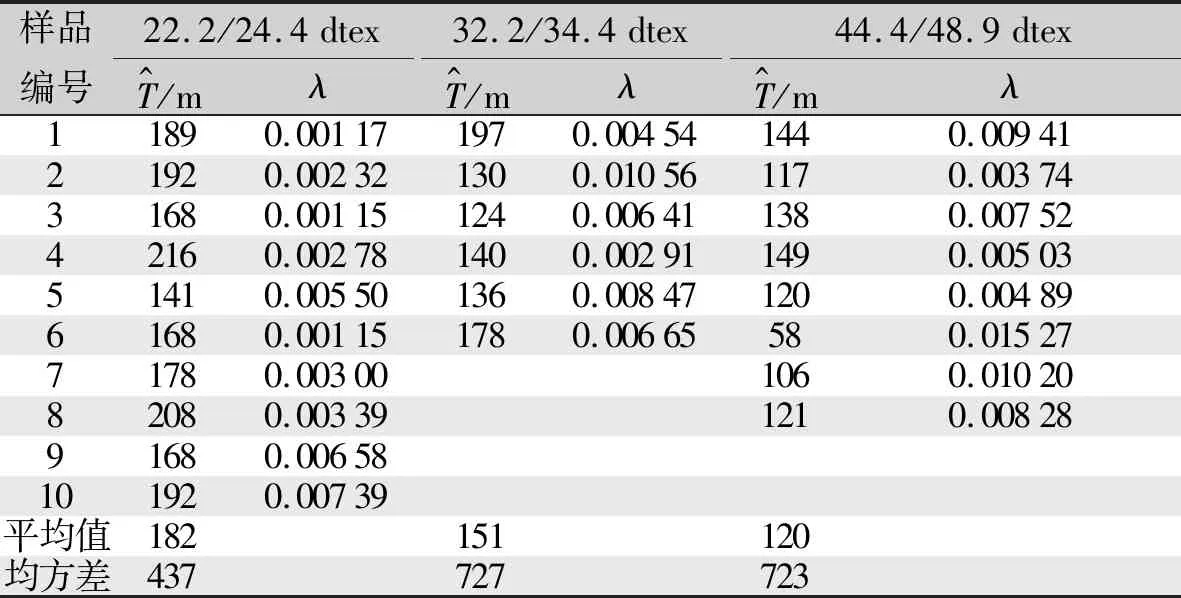
表1 生丝拟似周期及衰减率估算值Tab.1 Estimates of mimetic period and attenuation rate of raw silk

3.4 扩大检验丝长后参数估计

为了更准确地在生丝自相关系数曲线上获取拟似周期，根据式(3)对各组自相关系数数据进行了平移修正，消除部分不规则波动。生丝纤度序列取3.1中选出的六组样品，曲线如图3所示。

从图3可以看出，两位移动周期修正后，自相关系数曲线变得平滑，拟似周期更为明显；修正后的数据利用式(3)(4)计算得出λ、T，如表2所示。

表2计算结果显示，扩大检验丝长后拟似周期精度均有所提高，方差减小，22.2/24.4 dtex规格生丝拟似周期均值为186 m，λ的值在0.002 12～0.007 39变化；32.2/34.4 dtex规格生丝拟似周期为147 m，λ的值在0.003 19～0.011 49变化；44.4/48.9 dtex规格生丝周期在59～144 m变化，方差偏大，这是由于实际生产中44.4/48.9 dtex规格的生丝掐添较多导致部分周期较短，λ的值在0.002 89～0.007 16变化。理论上来说，随着生丝纤度增加，22.2/24.4 dtex、32.2/34.4 dtex、44.4/48.9 dtex三种规格生丝的拟似周期是依次变小的，实验结果与理论值拟合较好。

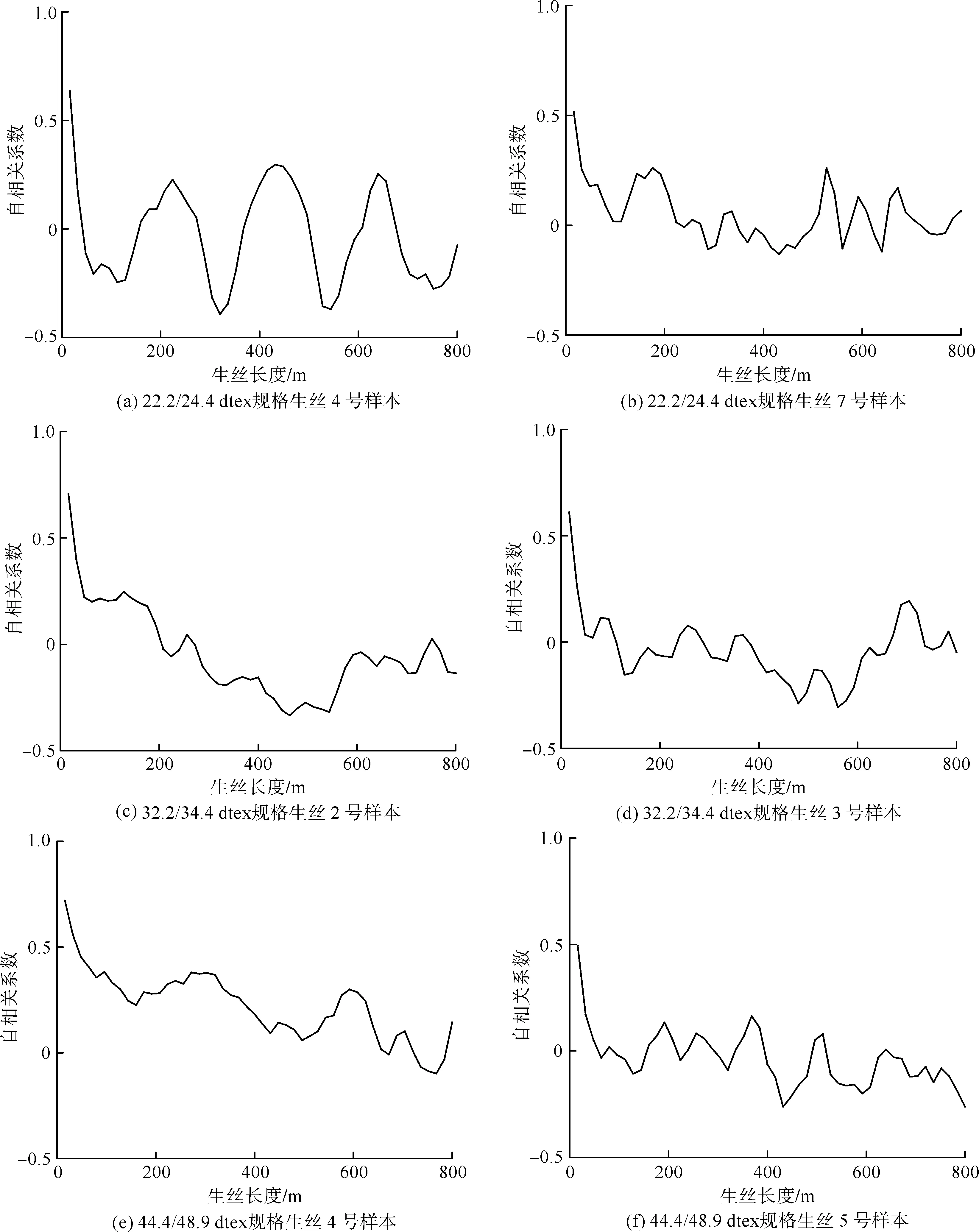
图3 扩大检验丝长后自相关系数曲线Fig.3 Autocorrelation coefficient curves after enlarging the test length

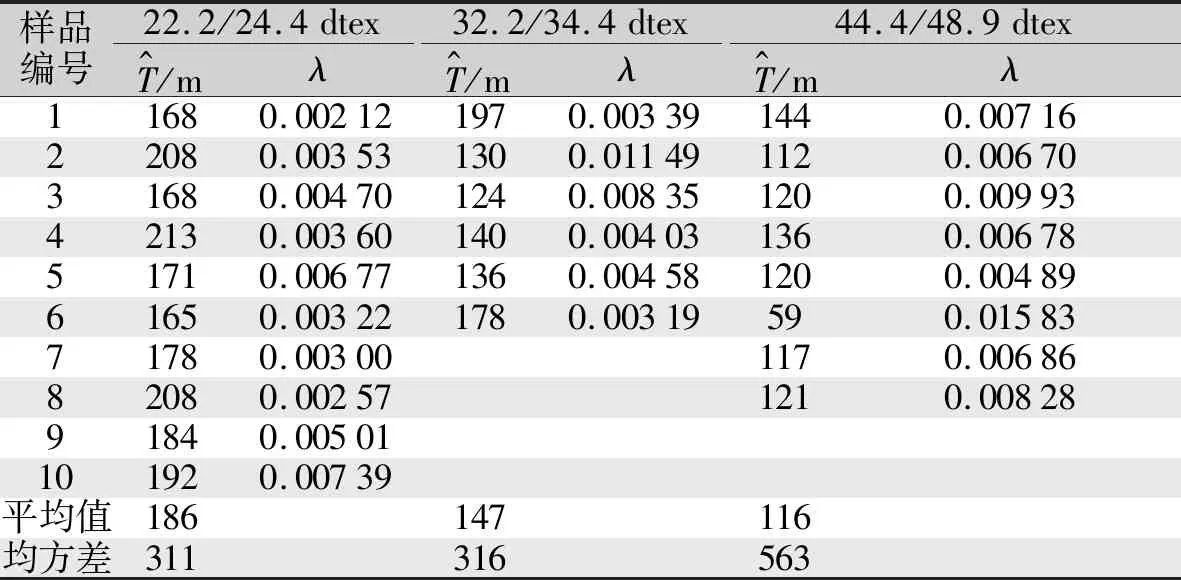
表2 消除微小误差后特征参数值Tab.2 The characteristic parameters after eliminating the small error

在实际生产中，拟似周期与衰减率在一定程度上反映了原料茧某些质量状况及缫丝过程相关的缫丝技术参数。比如说拟似周期与解舒丝长成正相关，解舒丝长长，拟似周期长；拟似周期与缫丝过程中单位时间内茧丝切断(包括自然落绪)次数成反比，切断多，拟似周期小；衰减率与解舒丝长的方差成正比，解舒丝长的波动大，衰减率大；衰减率与茧丝切断间距的方差成正比，茧丝切断间距波动大，衰减率大。因此，通过对生丝纤度序列这两个参数的调查，不仅可以为后续的计算机模拟试验提供数据，而且这两个参数在一定程度上也反映了原料茧的解舒丝长状况及实际的缫丝生产状况，对缫丝生产中缫丝技术的提高也有一定的参考意义。

4 结 论

本实验选取三种规格生丝样品，调查了生丝纤度曲线及自相关系数曲线，利用多点估计计算平均值的方法计算出参数特征值，得到以下结论。

1)本文建立的利用自相关系数序列的波峰点估算生丝纤度序列特征参数的估算公式，可以有效地估算出拟似周期与衰减率这两个特征参数。

2)对于自相关系数序列曲线中微小波动过多，影响波峰波谷等特征点的正确选择，这时可以扩大检验丝长，消除微小波动，提高拟似周期估算精度，比如本实验中将检验丝线长从8 m扩大到16 m后，特征点的选择就变得简单与准确。

3)计算结果表明三种规格生丝衰减率均随拟似周期增大而减小；低纤度的22.2/24.4 dtex规格生丝拟丝周期最大，周期变动频率较低；而高纤度的44.4/48.9 dtex规格生丝拟似周期小，周期变动频率较高。结果较真实地反应了生产中不同规格生丝的实际纤度变化状况。