基于激光全息法和泰伯效应的光学晶格制作与精确测量实验教学

梁文耀, 谭希超, 刘 基, 王 琪

(华南理工大学 a. 物理与光电学院； b. 物理教学实验中心； c. 电子与信息学院， 广州 510641)

0 引 言

近代物理实验是融合物理思想和实验技术的综合性实验课程，是我国高校物理类专业的必修实验课程之一[1-2]。然而其实验教学内容长期以来缺乏及时和有效的更新，难以反映当前物理学发展的前沿现状，迫切需要新增贴近物理学前沿的实验内容。本文提出将物理学研究热点之一的多光束激光全息干涉法制作光子晶体的理论引入近代物理实验教学。

光子晶体是介质或金属材料构成的人工周期结构[3]，被誉为“光子学半导体”。光子晶体由介电材料类比固体物理晶格排列制作而成，其独特的光子带隙、缺陷模、超准直、负折射等新颖物理效应引起了国内外学者的广泛关注[4-8]，人们据此提出了全向反射镜、光子晶体波导、非互易传输、光子晶体光纤等重要应用[9-13]。由于光子晶体的巨大潜在应用价值，设计和制作各种光子晶体成为人们的研究热点之一。人们已发展了半导体微电子加工技术、激光刻蚀法和激光全息法等多种制备方法[14-16]。其中半导体微电子加工技术比较成熟，但工艺复杂，成本较高；激光刻蚀法只能形成椭圆形状的单一刻蚀形状，而且制作微结构的效率较低。与其他方法不同，激光全息法是一种并行刻写的方法，它利用多束相干光在相干区域汇聚形成光强分布有序的周期干涉图样，利用“模板+填充”方式完成微结构的制作，可制作各种光学晶格微结构，具有灵活高效、图样丰富、大面积制作等独特优点。传统的激光全息法是让光刻胶在全息光路中曝光，从而产生周期微结构，需要大量制作实验样品，制作效率和成功率较低。本实验利用CMOS传感器代替光刻胶，将干涉结果实时传输到计算机进行分析，根据分析结果调节光路参数，无需曝光、显影等步骤，有效提升对微结构制作的掌控程度和降低实验成本。

为了便于分析实验结果，通常需要解决微结构的晶格常数测量这一难题。传统的方法是结合实验装置的光路参数通过公式计算得到。然而实际测量实验装置的参数时通常面临以下问题：① 在实验中干涉图样经显微物镜放大后由CMOS传感器采集图像输送到计算机进行观察，由于显微物镜的内部光路未知，同时显微物镜和CMOS传感器的相对位置不固定，从而导致图样的具体放大倍数未知；② 为了利用公式来计算晶格常数，需要精确测量实验光路的各项参数，例如万向镜光点之间的距离、光束夹角以及光点到成像点的距离等，这些参数在实际测量时难以精确测量，误差较大。因此迫切需要发展高效便捷的实验测量方法。

本实验中，提出一种基于泰伯效应(Talbot effect)的标定法来精确测量微结构的晶格常数。在同一实验环境下在显微物镜前放置一块光栅，让激光垂直入射，由于泰伯效应产生光栅的自成像。在不改变实验环境参数设置的情况下，光栅的自成像与激光全息法产生的光学晶格微结构放大比例相同，在已知光栅参数的情况下，将光栅的自成像作为参考导入Matlab进行分析标定，以自成像作为测量光学晶格的标尺，最终实现对光学微结构晶格常数的简便、精确测量。研究表明，实验结果与理论计算吻合得很好。

1 理论分析

1.1 多光束激光全息法基本原理

激光全息微结构制作是利用多束相干光在会聚区域产生干涉图案作为模板，进而通过光与物质相互作用形成折射率空间周期变化的二维或三维结构。改变光束波矢差和光束之间的夹角，能够产生多种周期结构。其干涉结果可看成是多束激光两两干涉结果的叠加。两束相干光干涉形成一系列极大值平行平面，其方向垂直于两光束所在平面，平行平面之间的距离由入射光波长和两光束之间的夹角决定：

(1)

式中：λ为入射光波长；θ为两光束夹角。

入射光多于两束时，两两光束间所形成的不同平面组数为n(n-1)/2，其中n为不共面的入射光束数。本实验主要研究二维晶格，取n=3，共有3组平行平面，它们在空间相交形成的极大值点在二维平面上具有良好的周期特性，这就是所谓的光学晶格点阵。N束相干光在会聚区域干涉的空间光强分布如下：

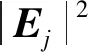
(2)

式中:Ej(r)、kj分别是第j束平面光波的复振幅和波矢。波矢差Gij=ki-kj，初相位差δij=δi-δj。

为了便于分析各束光的偏振组合影响，把参与干涉的各光束进一步分解为振动互相垂直、初相位彼此相差π/2的椭圆偏振光形式(Ea、Eb分别为椭圆长、短轴)：

Ej=Eja+Ejb=Ejaexp(ikj·r+δj)eja+

(3)

由式(2)可知：① 该干涉场分布具有周期性，可用于制作周期微结构。② 由固体物理学的正、倒易空间的变换关系可知，光束波矢差和倒格基矢存在对应关系，Gij可等效为周期结构的倒空间矢量，所以光学晶格的类型取决于Gij。③ 光束两两相干形成各种取向的一维晶面，其对比度、元胞形状依赖于光束振幅、偏振组合(如Ei·Ej)。

1.2 二维光学晶格的光束配置及晶格类型

利用式(2)研究干涉场空间分布I(r)的晶格类型与波矢差Gij的关系，即光束配置。各束光的波矢差与倒格矢存在对应关系，波矢差Gij可等效为干涉周期结构的倒空间矢量。如图1所示，要形成二维光学晶格微结构，需有3束非共面激光参加干涉，但仅有2个独立基矢，假设G1=G31=k3-k1和G2=G23=k2-k3，而k2-k1=G31+G23，并非独立基矢。倒格子基矢Gij的大小以及它们之间的夹角决定了正空间光学晶格的对称性。

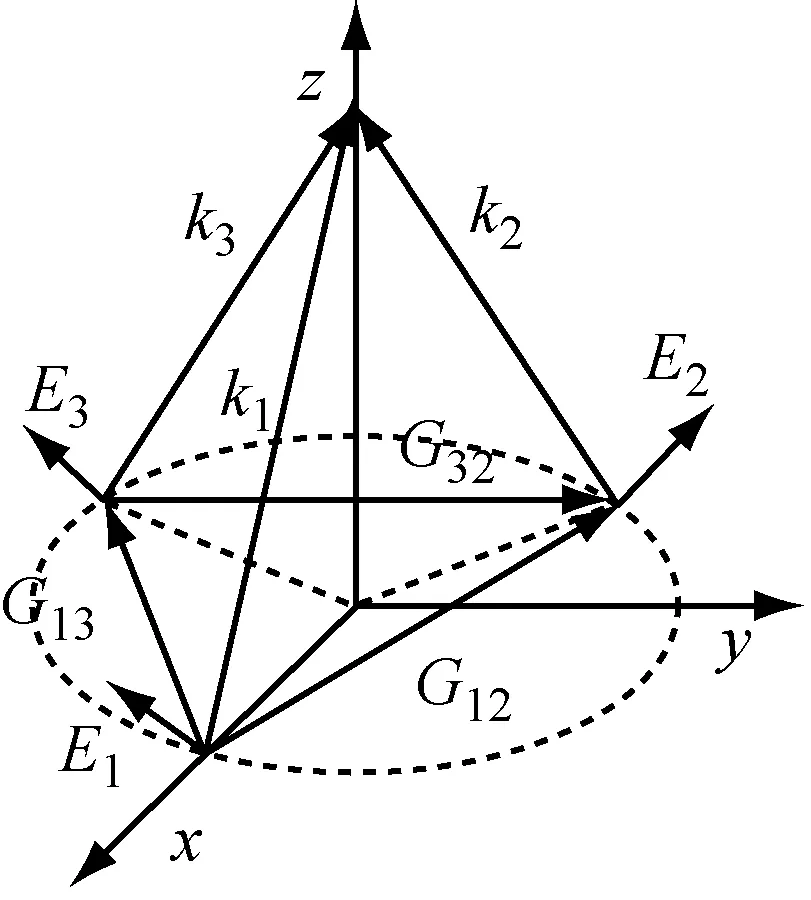
图1 二维光学晶格光束配置图

根据固体物理中的分类，二维晶格类型共有4种，分别为斜方晶格、矩形晶格、正方晶格、三角晶格，其条件分别如下：① 斜方晶格。最普通的二维周期结构，其条件为|G1|≠|G2|，且G1与G2的夹角不等于90°。② 矩形晶格。其条件为|G1|≠|G2|，且G1与G2的夹角为90°。③ 正方晶格：其条件为|G1|=|G2|，且G1与G2的夹角为90°。④ 三角晶格。其条件为|G1|=|G2|，且G1与G2的夹角为60°。不失一般性，后文以三角晶格为例开展实验研究，其他类型晶格可类似研究。图2所示为三角晶格的计算机模拟实例，相应参数见表1。

图2 三角光学晶格模拟实例

1.3 晶格常数测量原理——基于泰伯效应的标定法

泰伯效应：1836年，泰伯发现，用单色平行光垂直照射周期为d的光栅时，在光栅后距离为2m(d2/λ)

表1 模拟实例对应参数

上出现该光栅的清晰像，m为正整数，称最小重复距离d2/λ为泰伯距离。这种不用透镜即可对周期性物体成像的现象称为泰伯效应或自成像效应。此外，在(2m-1) (d2/λ)的位置上，会出现沿横向平移d/2的光栅像，周期仍为d。泰伯效应可用图3表示。

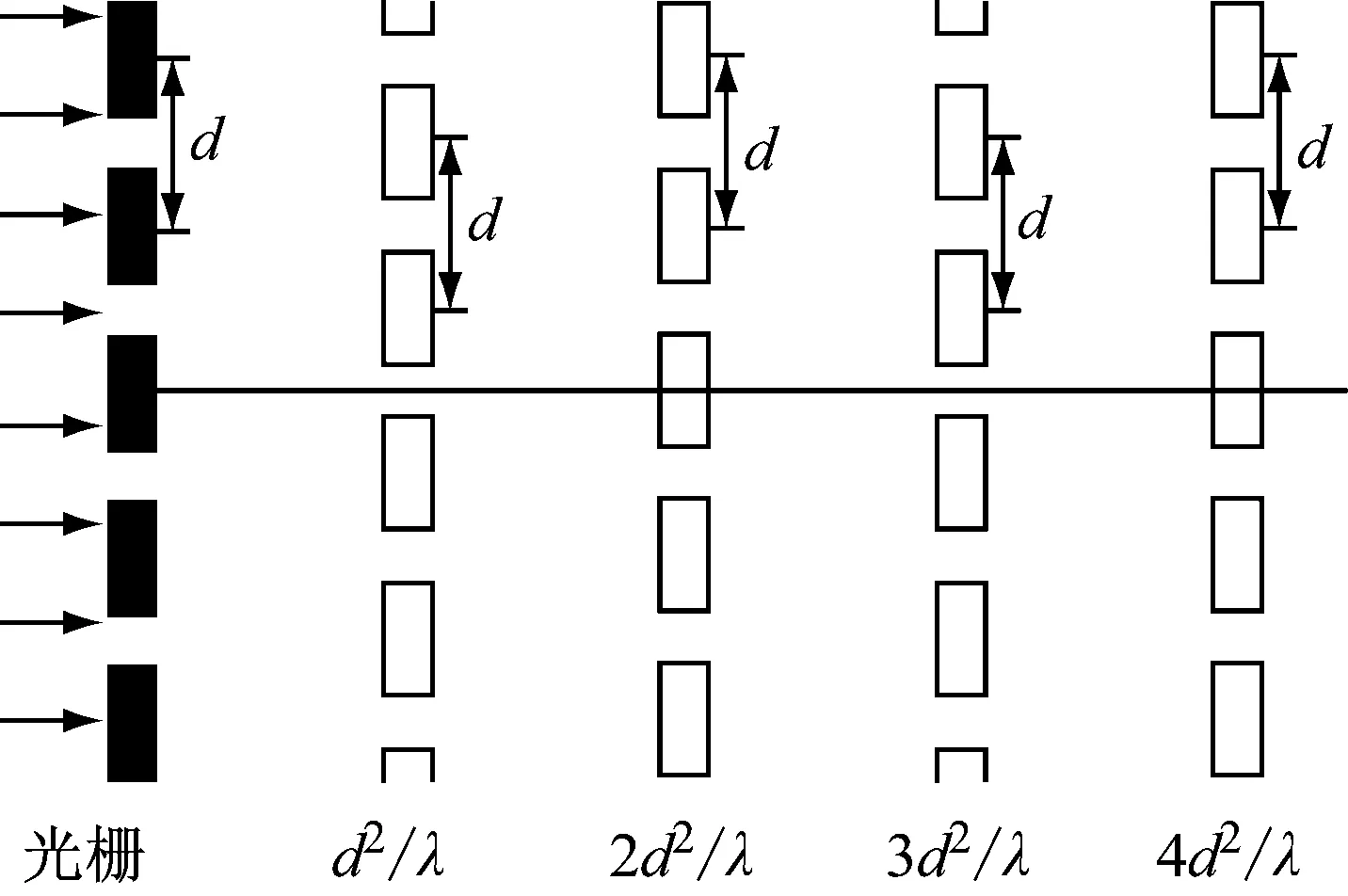
图3 泰伯效应

同一实验环境下，在显微物镜前放置一块光栅，让激光垂直入射。根据泰伯效应，近似为单色平面波的激光垂直照射光栅时，物体后会以泰伯距离为周期出现光栅的自成像。在不改变实验环境参数设置时，即保持显微物镜和相机的相对位置不变时，光栅自成像在CMOS传感器接收处与光学晶格的放大比例相同。在已知光栅参数的情况下，可以将泰伯效应引起的光栅自成像作为参考，通过标定法得到若干像素点之间的实际长度，以此为基础来测量光学晶格微结构的晶格常数。

2 实验设计及结果分析

2.1 实验方案及步骤

实验中采用单纵模连续半导体激光器作为光源，其工作波长为532 nm，功率约为 60 mW，线宽小于0.01 pm，相干长度超过50 m，偏振度大于100∶1，完全满足本全息干涉实验的要求。由于激光功率较大，为防止激光进入人眼造成危险，在激光器出口处放入中性滤波片减弱光强。具体实验方案及步骤如下:

(1) 搭建实验光路。图4为实验光路图，由平面光路和立体光路两部分构成，平面光路将激光分为3束，立体光路分为上光路和下光路。激光出射后经中性滤波片后由第1片分光镜获得2束光束，其中1束由全反镜和万向镜反射到显微物镜镜口处，为上光路的光束1；另1束经由第2片分光镜分光，再分别反射至显微物镜口，为下光路的光束2、3，在各束光路中均放置偏振片和1/4玻片用于调节各束光的偏振和光强。根据三角晶格的光束配置调整各光束方向，在显微物镜口会聚干涉，从而产生二维三角光学晶格。对于其他类型的光学晶格，可根据各自的光束配置调整干涉光夹角来产生相应的光学晶格微结构。

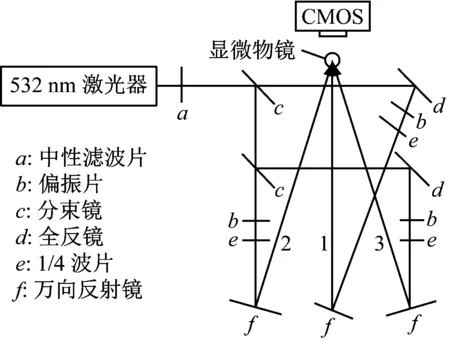
图4 实验光路图

(2) 将干涉产生的光学晶格图样传输至计算机显示，实时观察光学晶格图案。3光束干涉形成的微结构经显微物镜放大100倍，然后由CMOS传感器采集图像传输至计算机，在计算机上打开Microvision MV Camera Performance软件，实时观察放大后的二维光学晶格。

(3) 实时调整光路参数优化光学晶格。以干涉效果对比度为优化参数，实时观察和调节各光束的偏振和光强，达到最佳干涉状态和最高对比度。具体通过调节两两光束干涉实现，首先挡住第3束光，调节1、2束光达到最佳干涉状态；同理调节2、3和1、3两组光的干涉状态达到最高对比度；最后3束光同时入射产生三角晶格图案，图5所示为实验结果。

图5 三角光学晶格实验结果

(4) 在同一实验环境下产生泰伯效应自成像，用于后续测量晶格常数。已知所用光栅的参数为300 L/mm，保持实验环境参数不变，紧贴显微物镜口放置光栅，用分束后的某1束激光垂直照射光栅，结合计算机实时观察产生的自成像图案，缓慢增大光栅与显微物镜镜头的距离，获得成像效果最佳的自成像并保存，实验结果如图6所示。

图6 光栅的泰伯效应自成像

2.2 实验结果分析处理

首先，以泰伯效应产生的光栅自成像为参考，计算单位像素对应的真实长度并作为测量过程的基准量，测量三角晶格3个方向a、b、c上的晶格常数da、db、dc。然后计算晶格常数理论值，由前面理论分析可知，三角光学晶格可看成3组相干光两两干涉的平行条纹叠加而成，故可利用式(1)计算3组平行平面的间距，进而根据平行平面距离和晶格常数之间的几何关系计算晶格常数的理论值。最后将实验结果与理论值进行比较，讨论标定法测量的有效性。

2.2.1 基于泰伯效应标定法测量实验结果的晶格常数

(1) 取光栅自成像的图案，在已知光栅常数的情况下标定得到相邻像素之间的距离。如图6所示，在光栅自成像上选择跨越31条光栅线的线段作为标定线，长度共30个光栅常数，即30d，其中d为光栅常数；该线段两端点的像素坐标分别为(531,372)和(1 163，372)，相距共632个像素。已知光栅参数为每毫米300条刻线，故可得30d=0.1 mm。根据前面数据可求得相邻像素代表的实际距离δ=0.1 mm÷632=158.23 nm。

(2) 将实验得到的三角光学晶格图案导入Matlab，利用标定法测量其晶格常数。图7为3束光同时入射干涉产生的三角光学晶格，在该图样上沿晶格的周期方向a、b、c各取1段标定线段，其长度分别为39da、35db、42dc，其中da、db、dc为沿a、b、c方向的晶格常数，具体参数见表2。结合前面的δ=158.23nm计算得到的晶格常数为：da=2 788.37 nm、db=3 087.74 nm、dc=2 768.76 nm，从而完成晶格常数的实验测量。

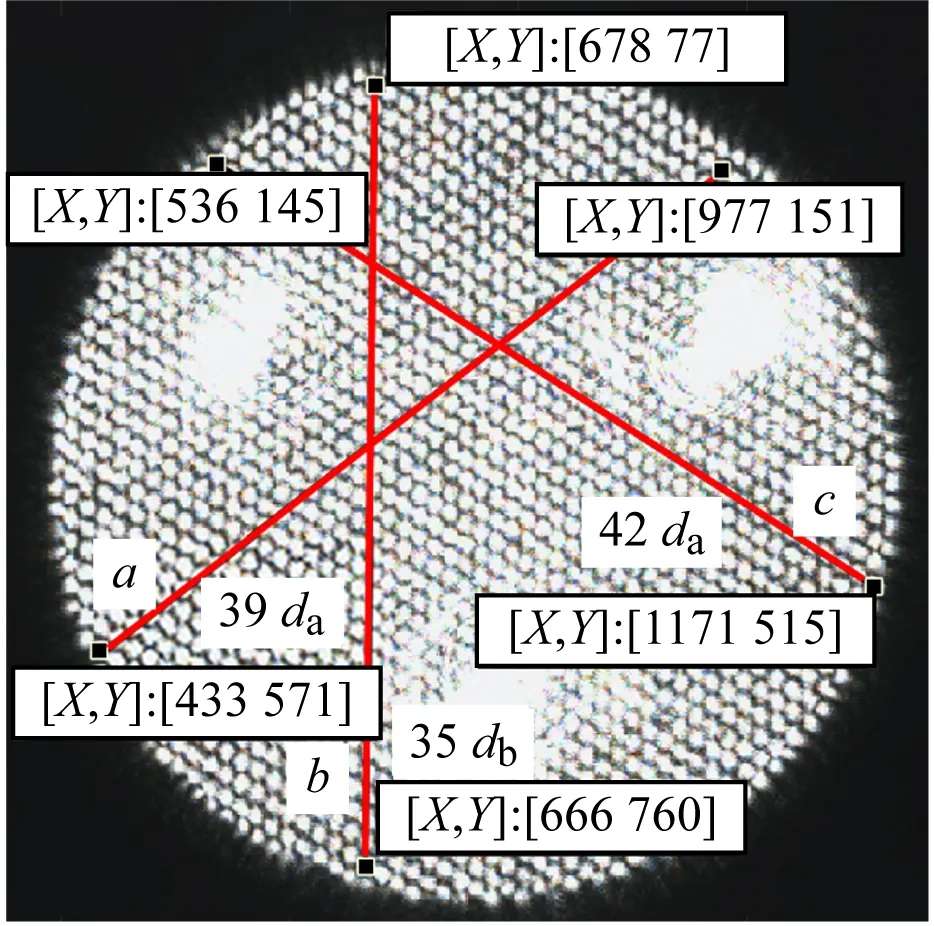
图7 三光束干涉实验结果

晶格周期方向端点坐标像素差晶格常数/(nm)a(977 ,151),(433 ,571)6872 788.37b(678 ,77),(666 ,760)6833 087.74c(1 171 ,515),(536 ,145)7352 768.76

2.2.2 晶格常数理论计算

下面对晶格常数进行理论计算，以便与实验结果进行对比分析。通过测量实验环境参数，可计算得到3组相干光两两干涉产生的平行面间距d1t、d2t、d3t，进而利用d1t、d2t、d3t和晶格常数dat、dbt、dct之间的几何关系，推导计算出晶格常数理论值，其中at、bt、ct代表理论计算中晶格的周期方向，具体见图8。

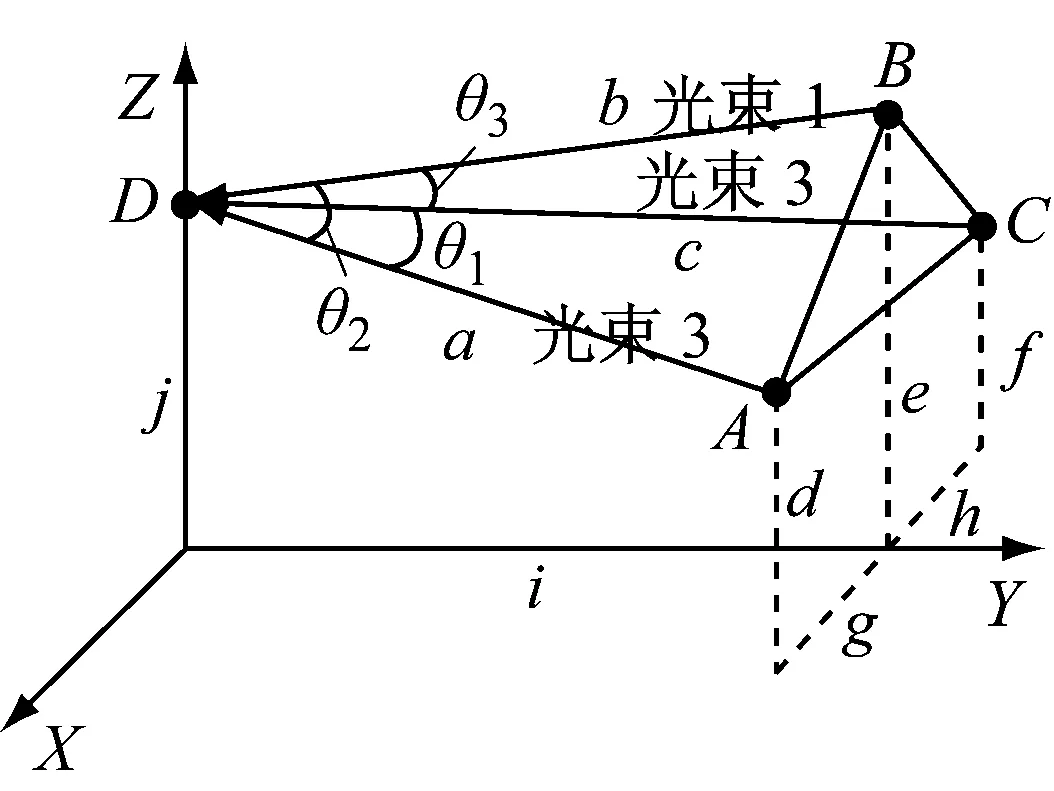
图8 条纹与水平方向的夹角

(1) 几何参数测量计算。图9所示为实验环境参数，需要说明的是，该图中为测量方便选取实验平台为XOY平面，所用坐标系仅用于计算几何关系，与图1的坐标系无关。A、B、C为万向镜上的光束反射点位置，D为干涉点，a、b、c分别为3束光从万向镜光点到干涉点距离。线段d、e、f、g、h、i、j可由直接测量得到，具体如下：d=f=16.9 cm，e=27.9 cm，g=h=7.5 cm，i=65.0 cm，j=21.2 cm，通过简单的几何关系计算得到：AB=BC=13.31 cm，AC=15 cm，a=c=65.57 cm，b=65.34 cm。可见三角形ABC为一等腰三角形。

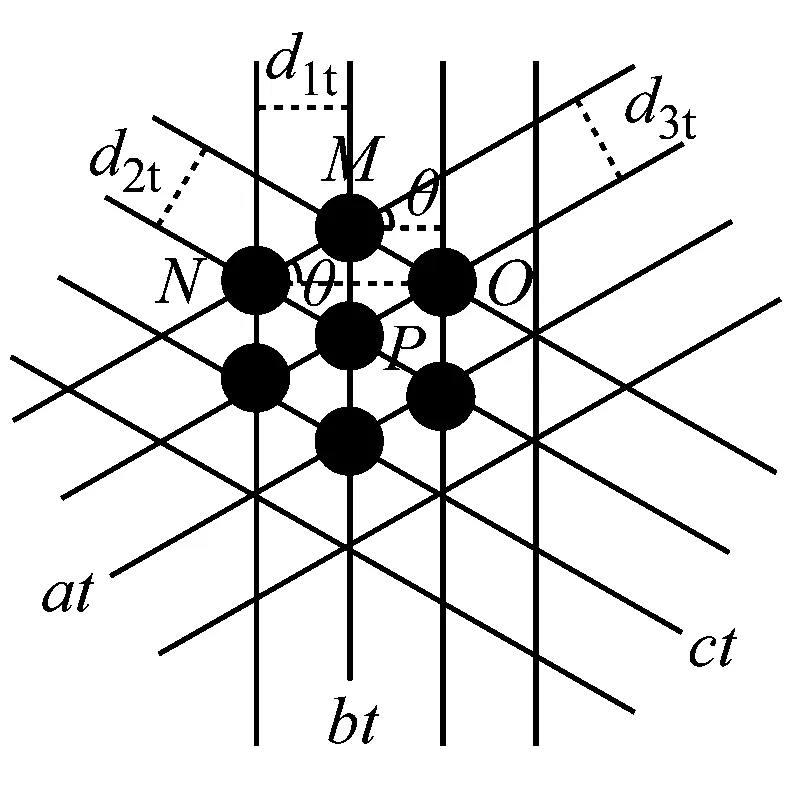
图9 实验光路几何参数

(2) 计算两两干涉条纹间距。在△ABD、△BCD、△ACD中，分别利用余弦定理计算得到(2, 3)、(1, 2)、(1, 3)3组光束组合的夹角分别为：θ1=13.13°，θ2=θ3=11.67°。由式(1)计算得到(2，3)光束组合的干涉条纹间距为d1t=2 325.55 nm，而(1，2)和(1，3)两组光束的干涉条纹间距相等，为d2t=d3t=2 616.46 nm。

(3) 计算晶格常数理论值。图10给出了条纹间距d1t、d2t、d3t和晶格常数dat、dbt、dct之间的几何关系。由sin(θ)=d2t/(2d1t)求得θ=34.23°，进而可求得晶格常数理论值为：dct=dat=d2t/sin(2θ)=2 812.83 nm，dbt=2datsin(θ)=3 164.53 nm，其中dct与dat的夹角为68°。需要说明的是，原计划设计光路产生三角晶格微结构，但是由于实际光路参数调节存在一定的误差，使得光路参数偏离了理想情况，将上述结果和三角晶格的参数条件比较发现实验结果略微偏离了完美三角晶格。

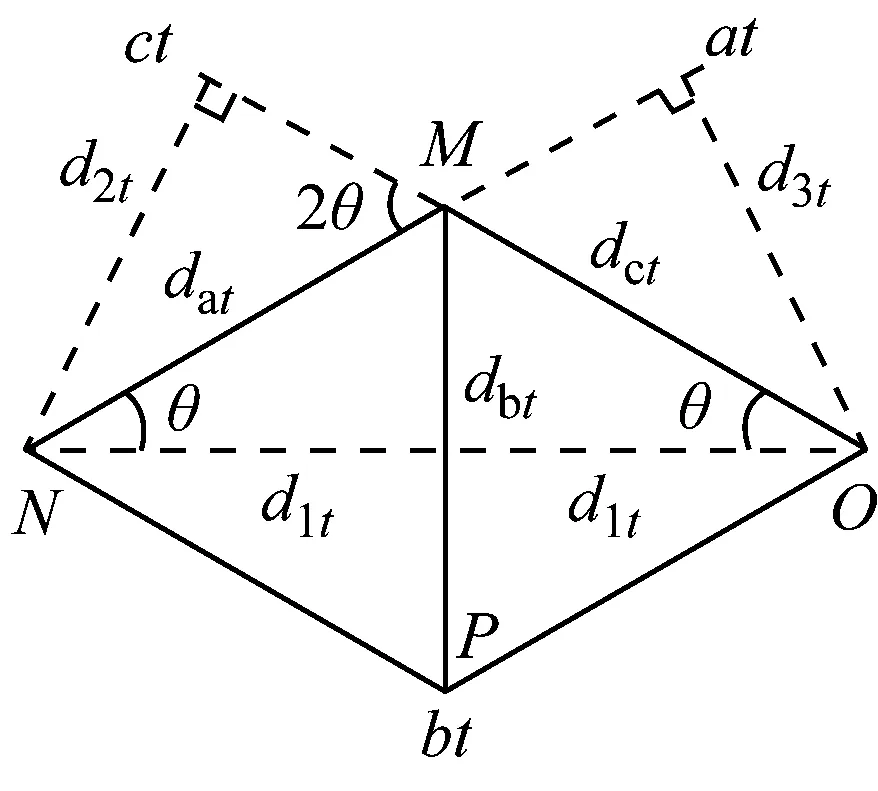
图10 条纹间的几何关系

2.3 结果分析和讨论

表3所示为实验结果与理论计算结果比较及相对误差。可以看出，理论计算结果和基于泰伯效应标定法测量的实验结果非常接近，最大相对误差仅为2.48%，可见实验结果和理论计算结果符合得很好。其误差来源于实验装置几何参数的测量误差和实验装置振动导致图像采集不稳定带来的偏差。综上可知，本文提出的基于泰伯效应的标定法可用来简便、快速、精确测量光学微结构的尺寸，无需复杂的实验参数测量和计算，是一种很好的微结构尺寸测量方法，可推广应用于测量更复杂的微结构尺寸。

表3 标定法测量晶格常数与理论计算对比

3 结 语

本实验结合多光束激光全息法和实时显示技术设计新型的全息实验，用于近代物理实验教学。以三角光学晶格为例探讨了光学晶格的产生原理和光束配置，并在实验中利用CMOS传感器实时传输干涉图样

到计算机进行观察分析。此外，提出一种新型的基于泰伯效应的标定法精确测量微结构的晶格常数，利用已知光栅在同一实验环境中产生的自成像作为参考，通过标定法方便快捷地获得晶格常数的实验结果，而且与理论计算结果符合得很好。该标定法无需测量实验光路参数，可用来简便、快速、精确测量光学微结构的尺寸，不仅巧妙克服实验光路参数难以准确测量的困难，而且避免了繁琐的计算，是一种高效的微结构测量方法。此外，本实验无需曝光和显影等步骤，具有形象、方便、高效等优点，有效降低了实验教学成本。