随机正交匹配追踪算法的热光鬼成像

高 禄， 亓晓曼， 肖 珂， 宋汉全

(中国地质大学(北京) 数理学院, 北京 100083)

0 引 言

鬼成像(Ghost Imaging, GI)，也被称为关联成像或者符合成像，具有传统光学成像所不具备的多种优点，如非定域性、超分辨率、无透镜成像以及抗干扰能力强等特点[1-2]。鬼成像系统中包括“闲置光”和“探测光”两个光路，“探测光”照射物体后的总光强值由一个不具备空间分辨率的探测器收集，即进行“桶测量”；“闲置光”光路中的光束自由传递至探测器，光强的空间分布信息被CCD(Charge-coupled Device)探测器记录下来。两个光路中的任何一路的观测数据都无法获得被测物体的信息，然而经过光场强度关联计算后却可获得被测物体的图像，因此人们形象地称之为“鬼”成像[3]。这种新型的量子关联成像方式在遥感[4-5]、医学[6]、显微成像[7]，以及弹载、星载成像探测[8]等各领域具有潜在的应用价值。

1988年，Klyshko[9]首次从理论上提出利用纠缠光子对进行关联成像的方案。1995年，史砚华研究小组首次利用纠缠光子对实现了量子成像和量子干涉实验[10]。2002年，Boyd等[11]首次利用经典光源实现了鬼成像，由此证明了非相干的经典光源也能够实现鬼成像，这一研究降低了鬼成像光源获取的难度，促进了鬼成像的实际应用发展。随后，计算关联成像、差分关联成像的提出以及压缩感知算法的应用研究，极大地提高了关联成像的信息获取效率和图像质量[12-18]。

对于空间频率非相干热光源鬼成像方案，获取待测物体图像信息需要对大量的采集数据进行统计平均，而高质量的图像必然要以庞大的数据量为代价。这样的采集过程很大程度地制约了成像效率，是鬼成像探测系统在实际应用中的一个最大弊端。本文通过理论研究与实验验证，在压缩感知鬼成像原理基础上[19-20]，提出随机正交匹配追踪算法，利用极少量测量数据即可再现待测物体的主要信息，从而能够更好地促进热光鬼成像系统在实际中的应用。

1 实验设置

实验装置如图1所示。He-Ne激光器发出的波长为632.8 nm激光束通过1个反射镜M的反射后，穿过两个偏振片P1和P2，之后光束照射到匀速旋转的毛玻璃RG上，产生了空间频率随机分布的非相干赝热光源。N为放置在毛玻璃RG之前的透镜组，用来调节照射到毛玻璃上的激光横截面尺寸的大小。实验中赝热光发出的光束穿过光阑Iris后，被50/50非偏振分束器BS分成光强相同的两束光。待测物体T紧贴探测器D1放置，光束经待测物体T后被探测器收集，进行“桶测量”，该光路称为测试光路；另一光路中的光自由传播到探测器处，探测器可获得光场横截面的光强分布，该光路为参考光路。实验中，可以通过调节光阑孔径的大小来控制赝热光源的横截面尺寸，进而调控关联成像的分辨率和可见度。BS距两个探测器和的距离均为30 cm，即探测光路和参考光路的光程相等。实验中所选择的待成像的物体是透射型的振幅物体，物体大小为1 cm×1 cm，透光部分呈字母“C”的形状，长宽均为600 μm，透光部分线宽为150 μm，其余部分均不透光。

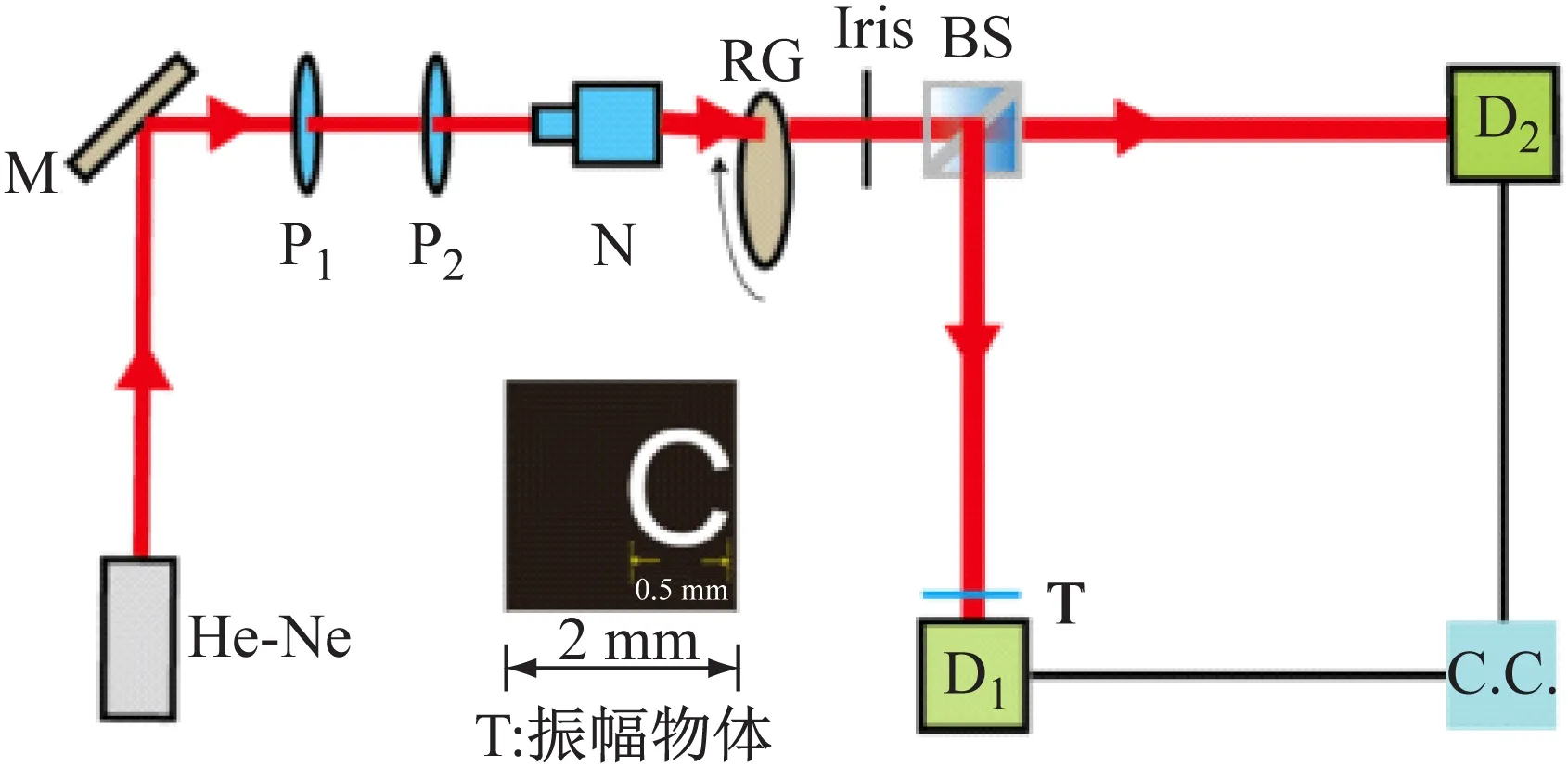
He-Ne-激光器；M-平面反射镜；P1，P2-偏振片；N-扩束器；RG-旋转毛玻璃；Iris-光阑；BS-50/50非偏振分束器；D1，D2-CCD探测器；T-待测物体; C.C.-关联测量

图1 热光源无透镜鬼成像实验装置图

2 理论分析

2.1 热光场二阶关联函数

热光关联成像的理论基础是热光场的二阶关联特性。被测物体的图像是通过两个探测器横截面光场的二阶关联函数所获取。根据高斯矩定理，当光场函数满足高斯统计分布时，高阶关联函数可以用一阶关联表示。热光场的二阶关联函数可以写作:

G(2)(r1,r2,t1,t2)=〈E*(r1,t1)E(r1,t1)〉·

〈E*(r2,t2)E(r2,t2)〉+〈E*(r1,t1)E(r2,t2)〉·

〈E*(r2,t2)E(r1,t1)〉=G(1)(r1,t1)G(1)(r2,t2)+

|G(1)(r1,t2)|2

(1)

式中：E(ri,ti) (i=1,2)表示探测器D1和D2处的光场函数；第1项表示探测器D1和D2处强度分布的乘积，理想情况下是一个常数，通常视为直流背景项；第2项表示光场强度的关联，即光场的关联信息。

归一化二阶关联函数可以表示为：

g(2)(r1,r2,t1,t2)=

(2)

g(2)在完全非相干光的理想情况下数值为2，在一般的部分非相干光源情况下，其测量值介于1和2之间，数值越接近2表明关联图像的可见度越高。

2.2 压缩感知算法

Candes等提出了压缩感知理论，该理论不同于传统的奈奎斯特采样定理。它指出，如果待测信号是可压缩的或者稀疏的，那么就能够使用一个观测矩阵将其投影到低维空间上，然后通过求解最优化问题，从投影中重构出信号。压缩感知算法打破了奈奎斯特采样定理的采样速率限制，将信号的采样与压缩编码同时进行。压缩感知包括稀疏表示、线性观测以及算法重构3个环节。

根据关联成像的基本原理，桶测量的每个观测值都与物体的透射函数T(x,y)有关。如果将桶测量第r次获得的探测值记为Br，Ir(x,y)，则表示参考光路的光强分布可以通过下式计算出具体值：

(3)

对物体进行M次采样后，可以得到M组Br和Ir(x,y)。为了恢复物体的透射函数，将桶测量值与参考光路的强度测量矩阵进行关联，即：

(4)

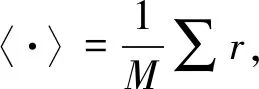
根据式(3)，将桶测量值Br作为观测值，将光强矩阵Ir(x,y)作为观测矩阵，则可以将信号重构问题归结为优化问题：

(5)

在压缩感知算法中，不同的重构算法得出的结果有很大的差异，本文主要对正交匹配追踪(Orthogonal Matching Pursuit，OMP)算法进行讨论。正交匹配追踪的核心思想是，每次循环通过计算残差与观测矩阵每1列的内积，找出内积最大也就是两者最相似的1列，然后根据最小二乘法就能够最大程度地求解出残差最小的原始信号估值。在运用OMP算法重构关联影像时，虽然能够将影像的主要信息提取出来，但是重构图像并不具有良好的连续性，信息缺失比较严重。尤其是在测量帧数比较多的情况下，算法恢复的图像并不会表现出较好的可见度和分辨率。这是由于在使用正交匹配追踪算法时，并没有充分运用所采集的待测物体的数据信息，随着测量帧数的增多，此缺点愈加明显。

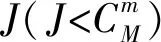
3 实验结果

3.1 热光鬼成像实验

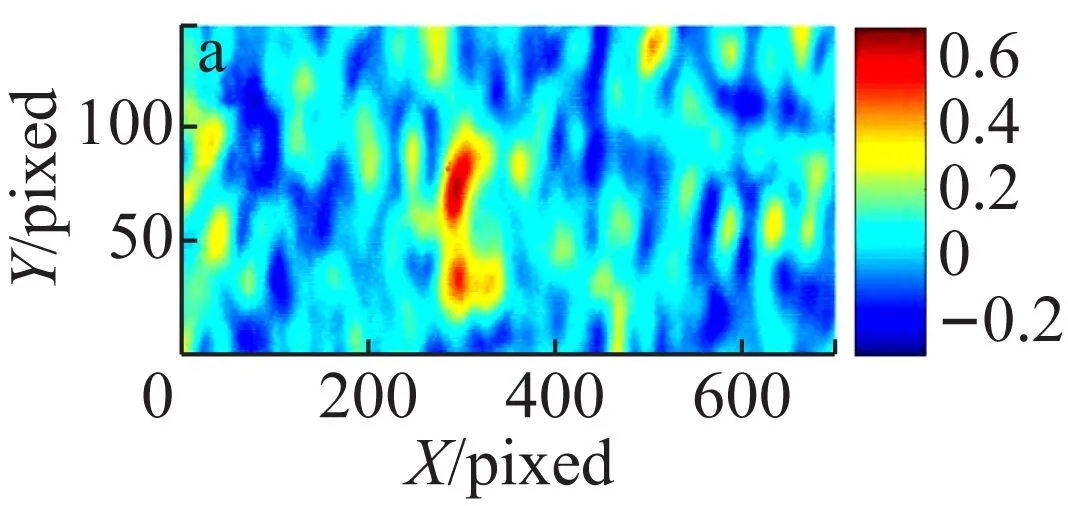
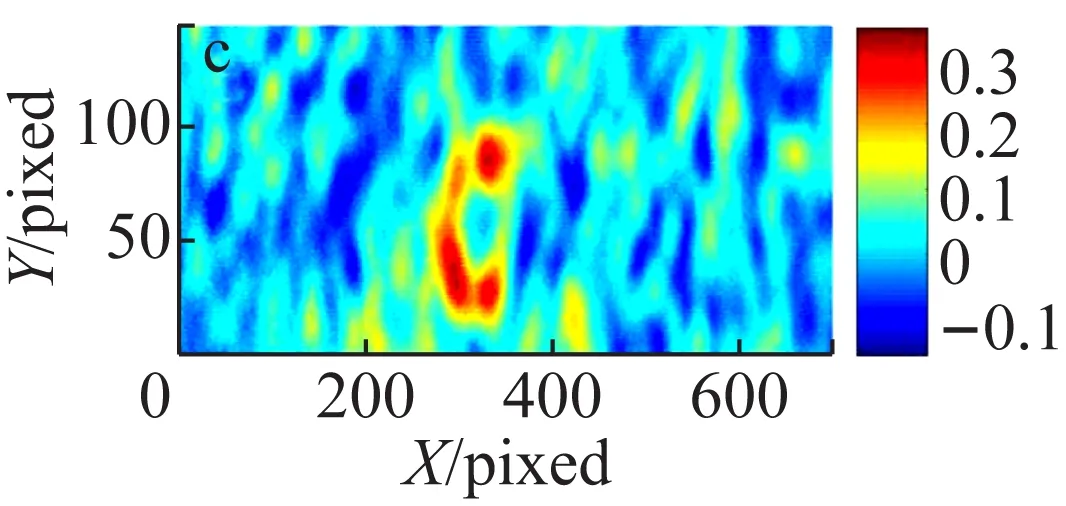
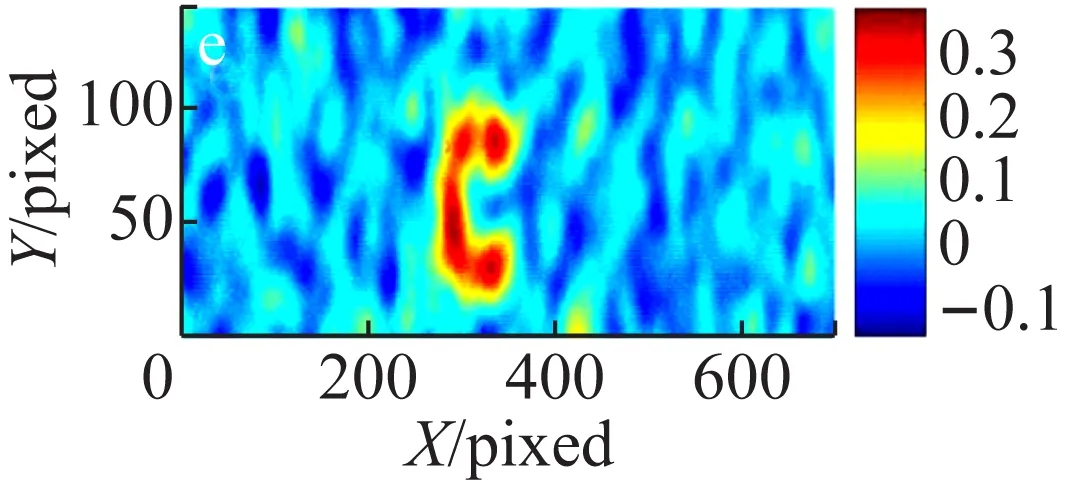
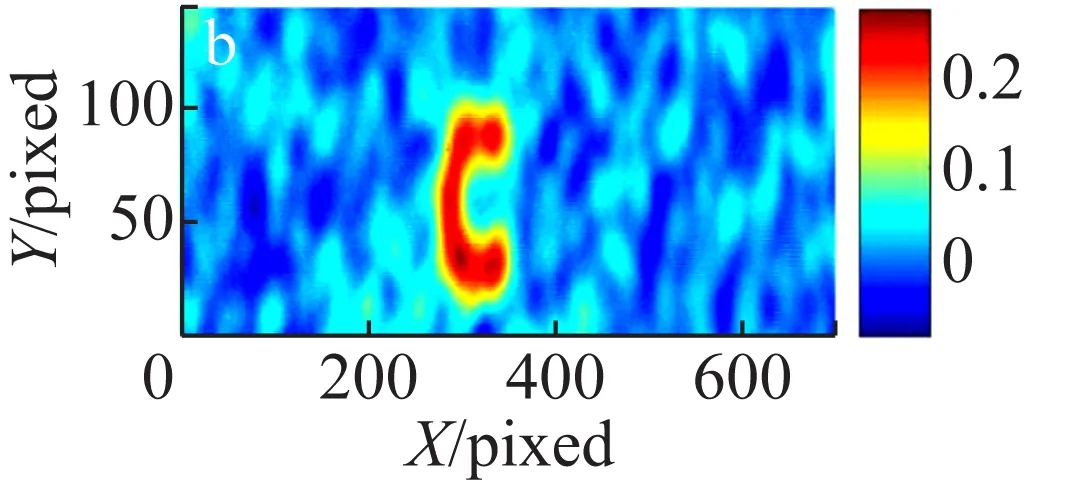
首先进行了热光鬼成像实验，所采用的实验方案为无透镜成像。实验中采集了不同的统计平均帧数，分别计算二阶关联函数值，实验结果如图2所示。图2的结果显示对于相同的实验装置和待成像物体，在实验参数完全相同的情况下，采集的随机帧数越多，图像的可见度越高。当统计帧数低于1 000帧时，图像质量随着帧数的增加明显提高。当统计平均帧数从1 000帧逐步增加到5 000帧时，图像质量趋于稳定，即当统计帧数达到一定数量时，图像质量保持不变。由此可见，若想进一步提高图像的质量，需要采用其他的方法。

(a) 100帧

(b) 300帧

(c) 500帧

(d) 1 000帧

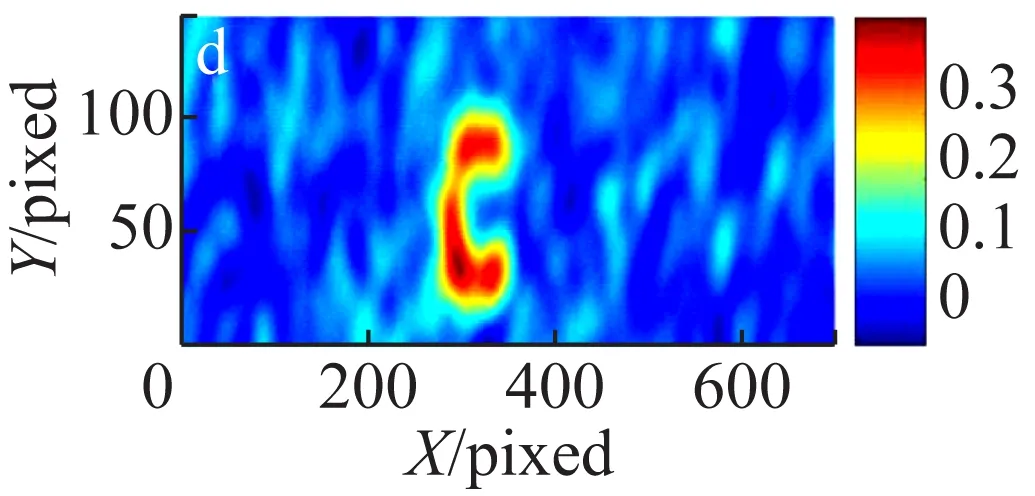
(e) 3 000帧

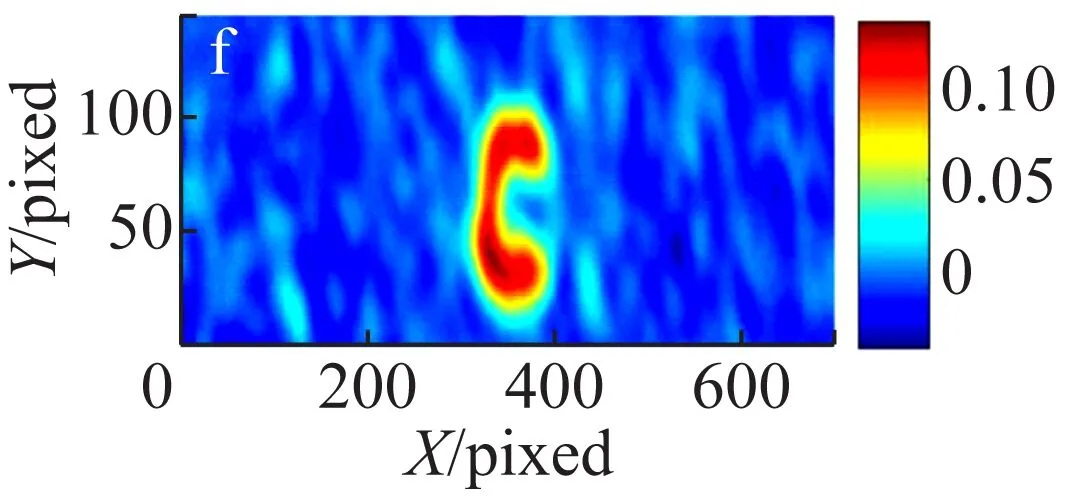
(f) 5 000帧

图2 不同统计帧数热光关联无透镜鬼成像结果

3.2 压缩感知算法鬼成像实验

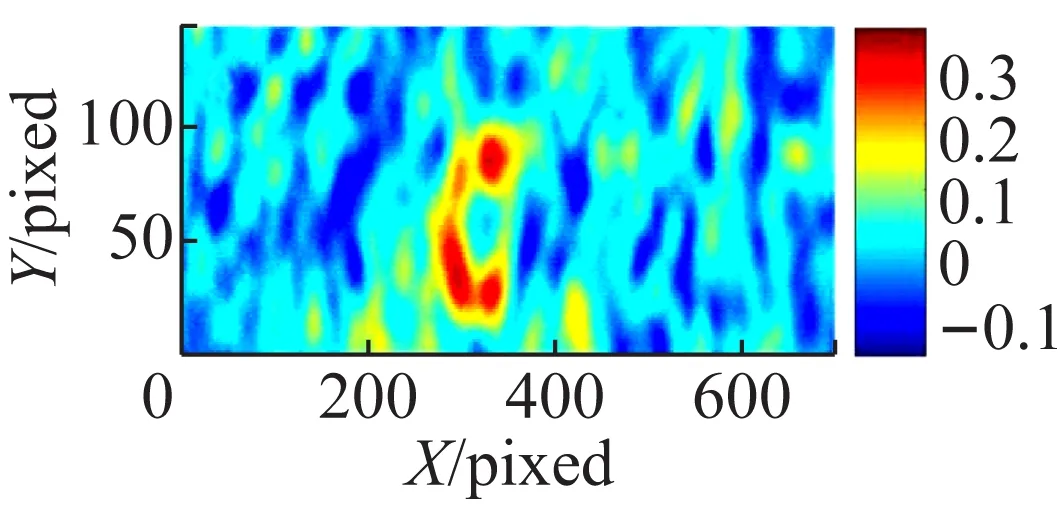
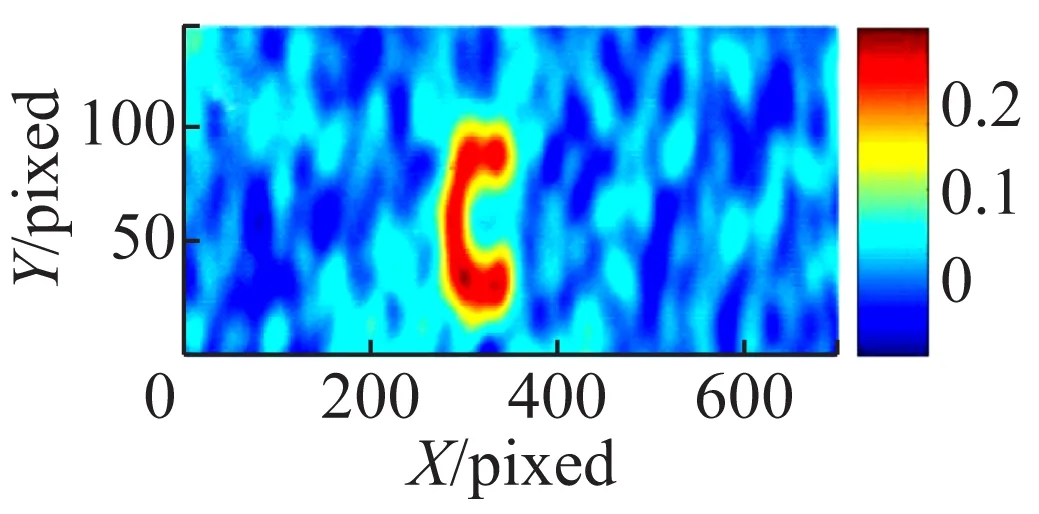
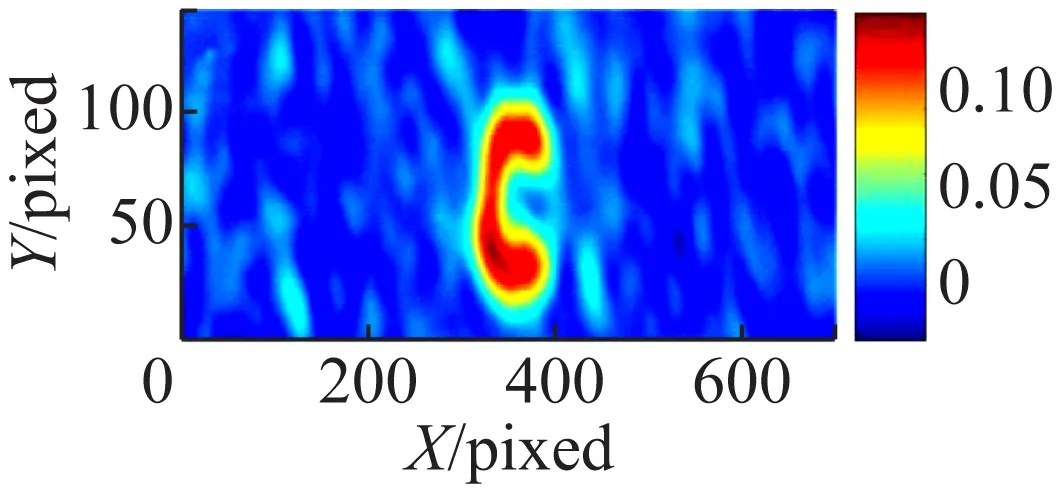
首先利用OMP算法针对300帧、1 000帧以及5 000帧的数据进行相对应的数据处理，将物体的主要信息从光强测量中提取出来，得到如图3所示的结果图。图3的结果显示，即使用少量的采集数据(如300帧)，也能够获得比较清晰的待测物体“C”的图像，1 000帧和5 000帧的OMP恢复图像结果相对于300帧的图像恢复结果而言，图像的连续性和清晰度有所改善，但是改善效果并不明显。

图3中的恢复图像与原始关联影像相比较而言，只有“信号”部分有数值，而其余部分都为零，因而可以认为图像的信噪比为无穷大。然而图像信噪比大幅提高的同时，由于数据缺失比较严重，只能利用算法恢复识别出物体的外形轮廓。由此可见，OMP算法能够在测量帧数较少的情况下实现对待测物体的外形轮廓识别，在远程非定域物体识别方面极具应用价值。

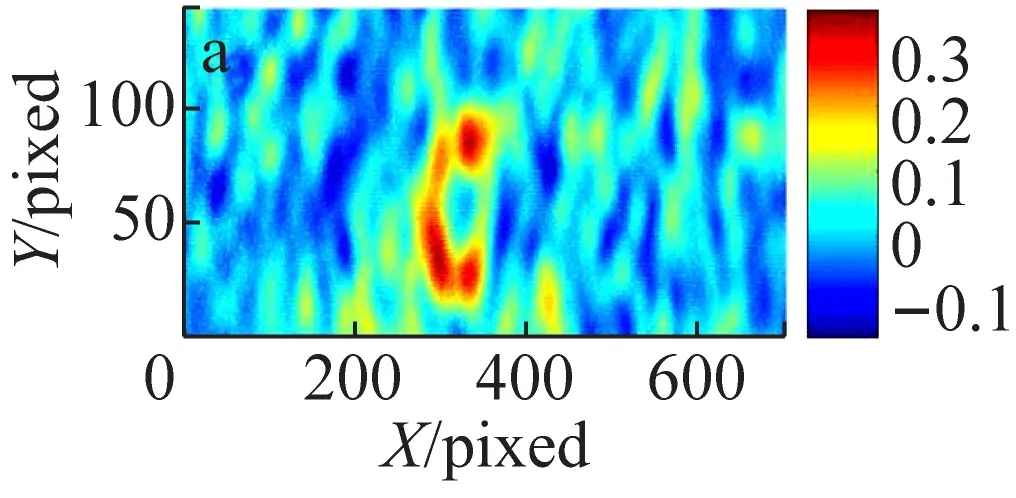
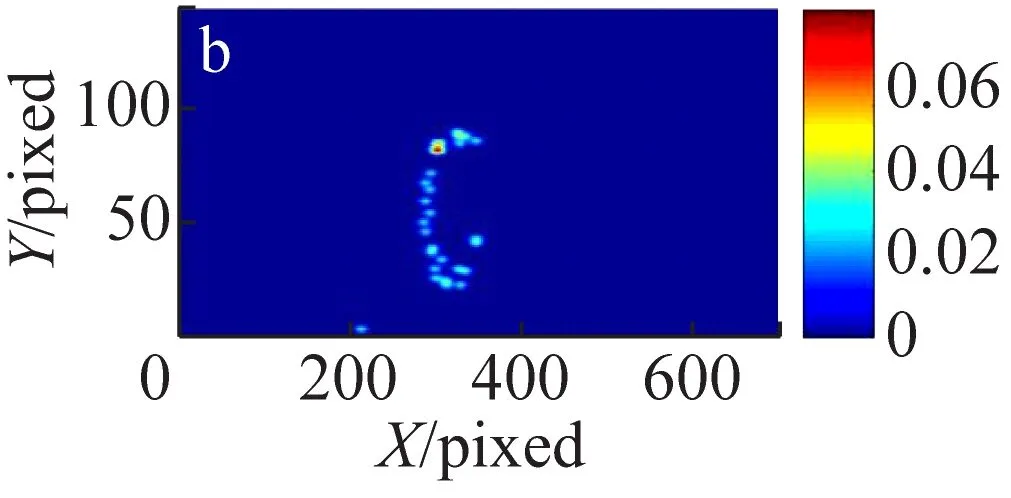
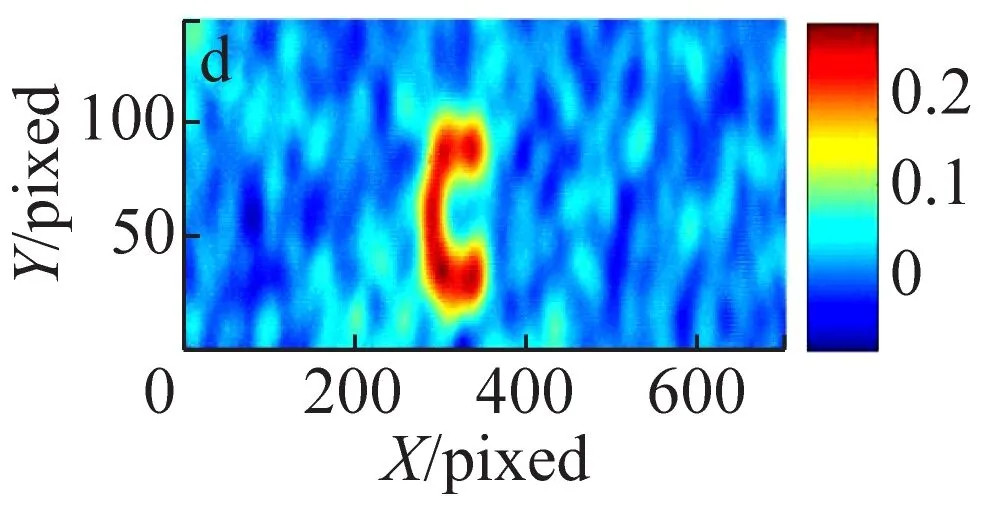
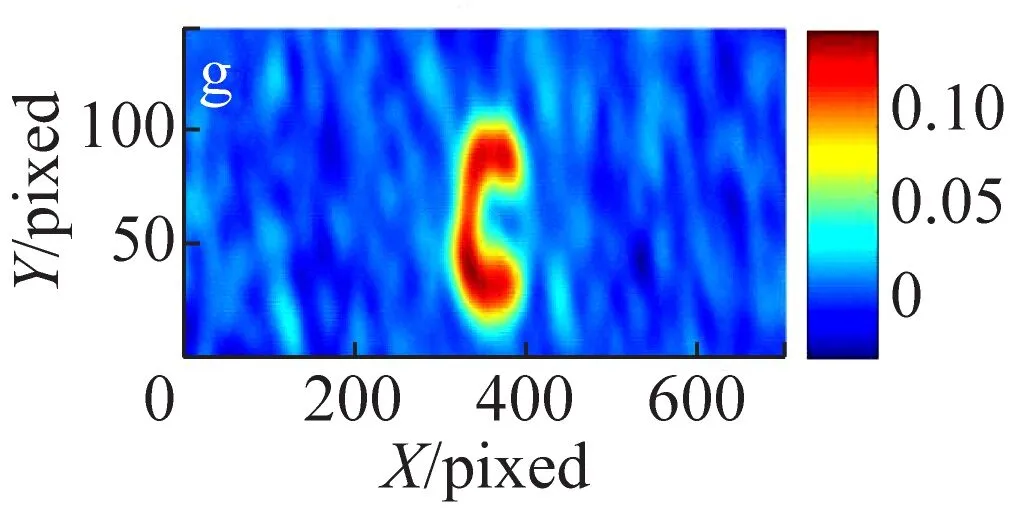
为了进一步提高热光关联成像压缩感知算法恢复图像的质量，在OMP算法的基础上提出RandOMP算法。对500帧、1 000帧以及5 000帧的原始数据进行处理，算法的处理过程为：从观测数据中随机选取了500帧数据进行一次OMP处理，共选取了500次得到500个OMP重构结果，然后对这500组结果求平均，最终得到优化解。将RandOMP处理的结果与原始热光关联以及使用OMP算法处理的图像进行了对比分析，所得结果如图4所示。

(a)

(b)

(c)

(d)

(e)

(f)

图3 OMP算法处理的热光关联成像结果

(a)，(b)，(c)分别表示300帧、1 000帧以及5 000帧的原始关联图像；(d)，(e)，(f)分别表示300帧、1 000帧以及5 000帧的经过OMP算法处理的结果

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

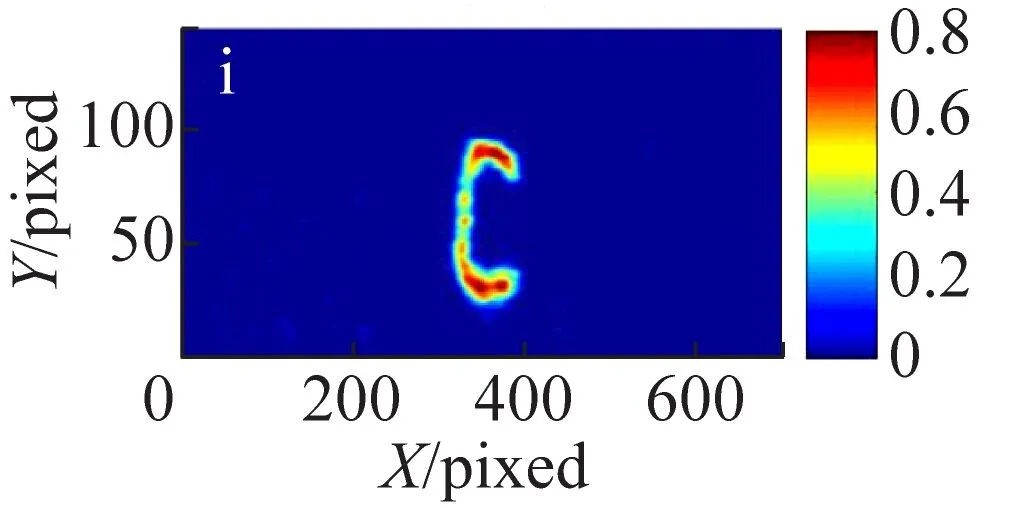
(i)

图4 热光关联图像、OMP处理图像及RandOMP处理图像结果

(a), (b)和(c)： 500帧关联图像、OMP和RandOMP处理结果；(d)，(e)和(f)：1 000帧关联图像、OMP及RandOMP处理结果；(g)，(h)和(i)：5 000帧关联图像、OMP及RandOMP处理结果。

将图3和图4的重构图像进行对比分析可以得知，RandOMP重构算法相比于传统的OMP重构算法而言，主要具有以下两方面的优势：

(1) RandOMP重构算法的运行时间更短。由于每次循环都是使用抽稀后的矩阵执行OMP重构过程，相比于直接使用原始矩阵进行OMP重构，运行速度明显提高。这种运行速度提高的优势会随着采集帧数的增加，测量矩阵的增大，而越发明显。

(2)RandOMP重构算法对图像信息的挖掘更充分，重构图像的质量更高。由图4给出的3列对比图像结果可以看出相同采集帧数的情况下，RandOMP的恢复图像连续性更好，更有利于对待测物体细节的分辨，这是因为RandOMP算法与OMP算法相比损失的图像信息更少。

4 结 语

将压缩感知的OMP算法应用于热光无透镜关联成像的实验方案中。实验结果表明，仅需要300帧的少量采集数据即可很好地将振幅型待测物体的信息提取，恢复出物体的外形轮廓。OMP算法为热光关联成像系统利用少量数据进行物体识别提供了可靠的科学依据。进一步，在OMP算法基础上提出改进的RandOMP算法，并且应用于热光关联成像实验中。实验结果表明，RandOMP算法可以明显地提高获取再现图像的质量，相比于OMP算法可以大幅提高重构图像的连续性，可以应用于热光关联成像系统在复杂物理环境下的探测。