分布式MVC-Kmeans算法设计与实现
2019-07-02
(长江大学电子信息学院,湖北 荆州 434023)
K-means算法[1]和Canopy算法[2]都属聚类成员,是一种无监督的模式分类法[3]。K-means算法实现简单,收敛速度快,但其聚类质量受初始聚类中心选取和类簇数影响较大。文献[4]以聚类对象分布密度为基础来确定初始聚类中心的选取;文献[5]采用最大距离不断划分最大距离簇,得到相距较远的初始聚类中心;文献[6]以数据点的距离构成最小生成树,对树剪枝将数据划分为k个初始聚类簇,获得初始聚类中心;文献[7]引入Canopy算法进行“粗”聚类,获得了K-means算法的类簇数k和聚类中心。
以上这些方法都只是在串行化条件下对K-means进行了改进,随着数据量增长,传统K-means以及改进的K-means算法已很难满足需求,因此,学者们提出了基于云平台的分布式K-means方法。文献[8]采用最小加权距离确定数据点被划归的类簇,增加收敛性判定,最终聚类准确率、收敛时间都有明显提升,并利用Hadoop平台[9]的MapReduce编程框架[10],将算法扩展至大规模数据集,扩展性和加速比的结果表明该算法适于海量数据处理。文献[11]根据样本密度剔除孤立点,利用最大最小化距离思想选择k个初始中心,使初始聚类中心点得到优化,利用MapReduce模型进行了并行化处理,提高了聚类结果准确率和稳定性,同时很好地将算法扩展至大规模数据处理。文献[12]引入Canopy算法优化K-means初始中心的选取,并利用MapReduce框架进行并行化,算法能获得较好的执行效率和优良的扩展性,适合海量数据的聚类分析。
针对文献[7]和文献[12]引入的Canopy算法未考虑任选的初始中心可能是离散点或是孤立点的问题,笔者以样本密度表征类内聚集度[13]程度,利用样本方差和最小方差改进Canopy算法的初始中心选取,并参照文献[6,7]设定了Canopy中的阈值,提出了一种利用最小方差获取Canopy最优全局中心作为K-means聚类中心初值的算法(简称MVC-Kmeans,K-means based on the Minimum Variance Canopy)。
1 相关知识
在实际应用中,K-means算法通过设置k个初始聚类中心,对待测数据集根据距离准则反复迭代更新聚类中心并进行聚类划分直至收敛;Canopy算法根据随机选取的初始Canopy中心和给定的阈值T1和T2(T1>T2)[14],按照距离准则对待测数据集进行阈值划分,最终生成互相重叠的Canopy类。通常k值、初始聚类中心以及T1和T2大多根据经验或者随机选取,带有很强盲目性,对最终聚类质量有较大影响。因此对上述初值确定是笔者研究重点。
设待聚类数据集为D={xi|xi∈Rm,i=1,2,3,…,n},其中数据集每个样本拥有m个属性,数据xi可表示为xi=(xi1,xi2,…,xim)。
定义1样本xi和xj的欧氏距离:
(1)
定义2样本xi到所有样本距离的平均值:
(2)
定义3样本xi的方差:
(3)
定义4待聚类数据集的平均距离:
(4)
定义5误差平方和:
(5)
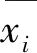
2 分布式MVC-Kmeans算法思想
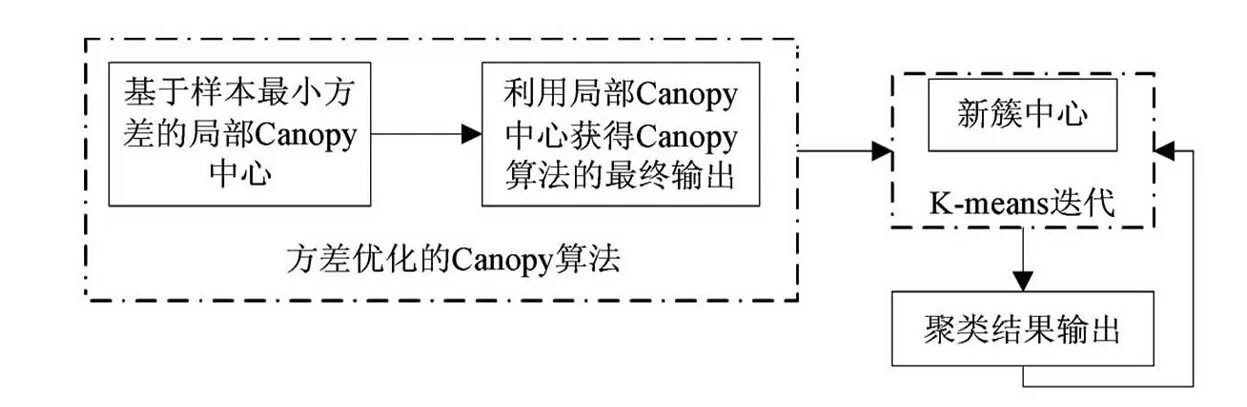
图1 MVC-Kmeans执行流程图
依据样本方差原理,数据集中样本方差的大小,直接决定样本在数据集中的离散趋势。方差越小,则样本点周围数据越稠密,收敛越快;反之,则越稀疏,收敛越慢。因此,对Canopy算法随机从待聚类样本中任选一点作为Canopy中心的方式进行优化,利用式(1)~(3)计算样本数据集中每个样本的方差,以样本方差最小点作为Canopy中心进行Canopy划分来获取优质的初始聚类中心作为K-means算法的输入,同时参照文献[5,6]设置Canopy中的阈值。其执行流程图如图1所示。
3 MVC-Kmeans算法步骤
算法步骤描述如下:
步1Canopy阶段获得局部Canopy中心。
a)令t=0,根据式(1)~(3)获取每一个数-据集D的样本方差集合C,同时依据噪声点和孤立点存在hi>hAV,为消除这些点的影响以及基于T1与T2之间存在的关系,设定T2=hAV,T1=2T2。
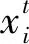
则将xj加入到Ct集合并C=C-Ct;
则将xj加入到Ct集合且该点可能会成为下一个Canopy中心;
else
xj可能会成为下一个Canopy中心;
d)若C为空,则获得W={wt|wt∈Rm,t=1,2,3,…,n}结束;否则,转到步1b)。
步2获得Canopy算法的最终输出。
a)令t=0,将W以式(1)~(3)获得的每个样本方差放入集合K,设定T2=hAV,T1=2T2。
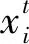
则将xj加入到Ct集合并K=K-Ct;
则将xj加入到Ct集合且该点可能会成为下一个Canopy中心;
else
xj可能会成为下一个Canopy中心;
d)若K为空,则获得G={gt|gt∈Rm,t=1,2,3,…,n}结束;否则,转到步2b)。
e)将重叠区域的样本归入到与所属Ct的gt距离最近的Ct中,并计算各个Ct的样本与对应gt和的均值,作为全局的Canopy中心,并更新集合G。
步3K-means阶段构造初始划分。
a)以G为K-means的初始聚类中心,利用式(1)计算D中各样本到各初始中心的距离,根据相似性原则将样本划归到最相似的类簇中。
b)计算每个类簇的平均值作为新的聚类中心。
c)根据式(5)计算当前聚类结果的误差平方和E。
步4重新构造类簇及更新聚类中心。
a)以新的初始聚类中心作为聚类中心,利用式(1)计算D中各样本到各初始中心的距离,根据相似性原则将样本划归到最相似的类簇中。
b)计算每个类簇的平均值作为新的聚类中心。
c)根据式(5)计算当前聚类结果的误差平方和E′。
d)如果E′-E<ε,则聚类收敛,算法结束;否则,令E=E′,转到步3。
4 分布式MVC-Kmeans算法的并行设计
MVC-Kmeans算法的执行流程如图1所示,由两部分组成。在Hadoop平台的MapReduce下进行了该算法的并行化设计,其包含2个任务,依次执行,前一个任务的输出将是下一个任务的输入。
任务1:结合最小方差和Canopy算法思想在MapReduce编程框架下的实现。
在Map阶段,利用分布在集群不同站点的数据子集,通过Canopy算法快速产生若干个以最小方差划分的局部Canopy中心和重叠的Canopy;在Reduce阶段,对Map阶段输出的Canopy中心重新计算后,以方差最小的样本为新的初始Canopy中心,再次运用Canopy算法获得全局Canopy中心和重叠的Canopy,将重叠区域的样本归入到与所属Canopy的Canopy中心距离最近的Canopy中,并计算各个Canopy的样本与对应Canopy中心和的均值,获得K-means算法的初始聚类中心。整个阶段的算法设计流程如图2、图3所示。

图2 最小方差Canopy-Map阶段 图3 最小方差Canopy-Reduce阶段
任务2:该部分是传统K-means算法在MapReduce编程框架的实现。
在Map阶段,将来自于任务一的输出作为全局的初始聚类中心,通过对逐行读取的数据按照就近原则进行划分归类;由于Map阶段输出的大量结果会写入磁盘,当Reduce阶段启动时需要通过网络来获取这些结果,严重消耗磁盘IO和网络IO,为了优化MapReduce中间产生的结果,设计了Combine阶段,对于来自于Map阶段的输出,以Key相同的各个Value进行合并;在Reduce阶段,读取每个Combine阶段处理后的数据样本个数N及各样本维度的坐标值,并将各维度的值对应相加求均值,获得新聚类中心来更新原聚类中心,然后进入下一次迭代直至算法收敛。其K-means算法并行化设计如图4所示。
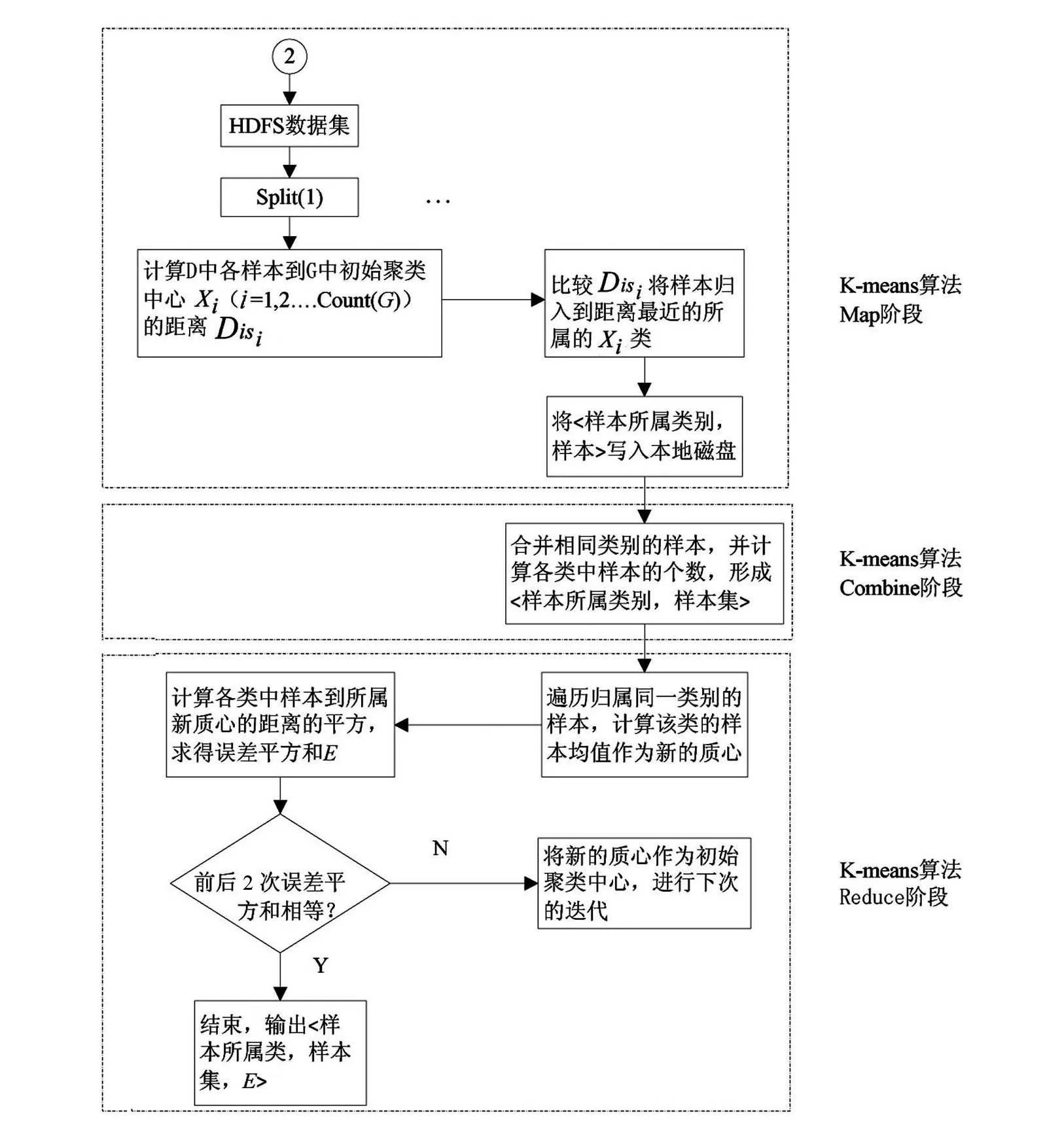
图4 K-means算法并行化设计
5 试验与分析
Hadoop平台由1台主节点和3台从节点构成,对来源于公开UCI机器学习库[15]中的数据集进行试验分析。为了验证MVC-Kmeans算法的准确性和收敛性,与传统的K-means算法进行了比较;同时,
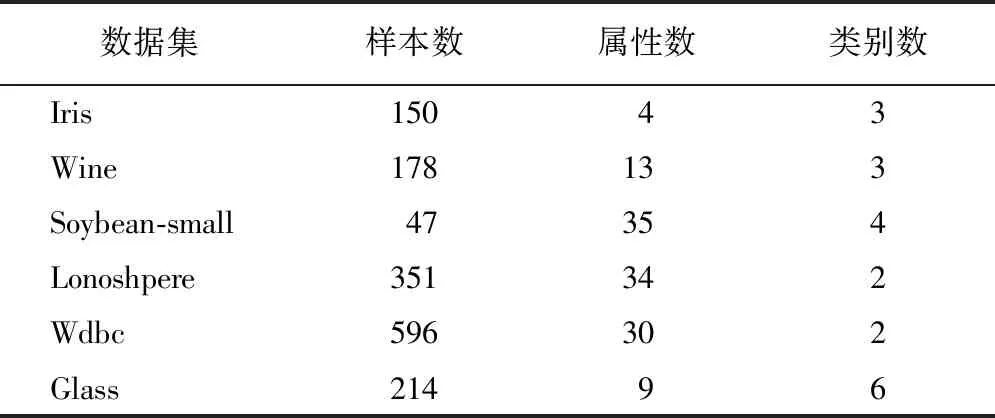
表1 试验测试数据集
为了验证MVC-Kmeans算法处理大规模数据的优势,进行了加速比和扩展率的分析。
5.1 试验数据
表1列出了所选样本的属性、样本数量以及类别数。这些标准数据集用来准确率量算法的聚类质量。
同时,为了符合MapReduce编程框架的数据格式要求,所有的数据以
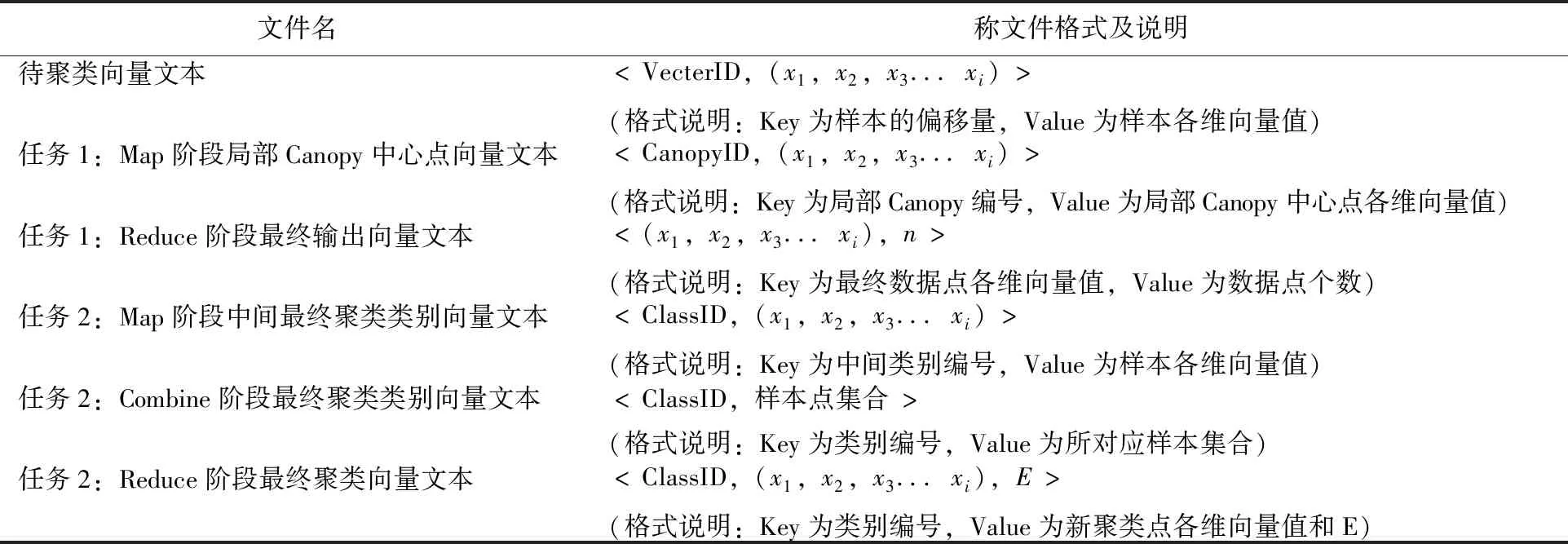
表2 试验各阶段数据格式
5.2 试验结果及分析
1)MVC-Kmeans算法与传统K-means算法聚类质量的比较 利用表1数据集对优化的算法在单机上进行了检验。为了保证检验的结果可靠,每个样本集在各算法下分别进行10次,结果取10次试验的平均值,其试验结果如表3所示。

表3 样本数据集试验结果
从表3中可以看出,MVC-Kmeans算法在所选数据集上聚类精度均有提高,提高了4.11~25.91个百分点;误差平方和与迭代次数均有降低,其降低幅度分别为4.70%~34.00%和16.67%~42.86%,可见MVC-Kmeans算法能获得较好的聚类质量和更快的收敛速度
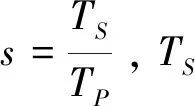
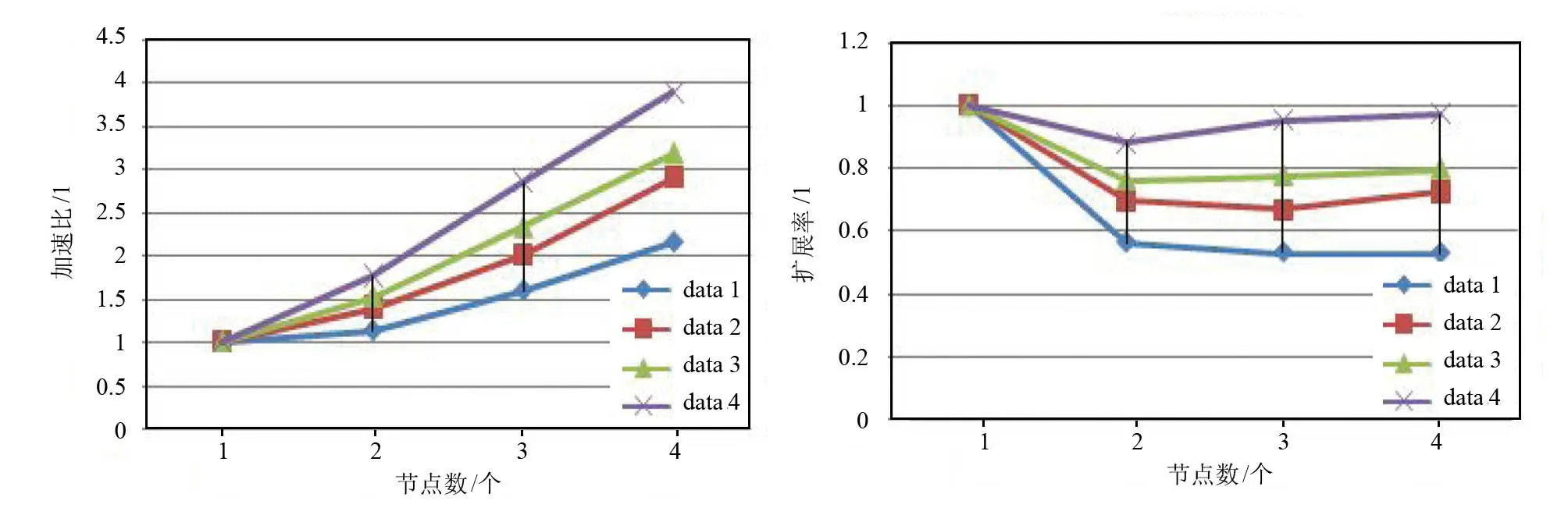
图5 Iris数据集加速比测试结果 图6 Iris数据集扩展率测试结果
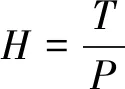
6 结语
笔者基于最小方差和Canopy算法优化了K-means算法初始聚类中心选取,提出了MVC-Kmeans聚类算法。在Hadoop云计算平台上,对MVC-Kmeans算法进行了MapReduce并行化设计。在开源数据集上相比传统聚类算法的试验结果表明,无论是在准确率、迭代次数还是误差平方和,MVC-Kmeans算法明显优于传统K-means算法,能获得更加稳定的聚类结果以及更快的收敛速度,并适于大规模数据的聚类分析。但对于Canopy算法中阈值T1与T2的选择不具备确定性,这将是下一步要开展的工作。
