移动荷载作用下地下结构损伤识别方法

2019-07-02刘雨彤王胜楠朱宏平

土木工程与管理学报 2019年3期

罗辉，刘雨彤，王胜楠，朱宏平

(1. 华中科技大学土木工程与力学学院，湖北武汉 430074；2. 陕西省西安市新城区西一路街道办事处，陕西西安 710004)

随着列车运行速度的不断增加，列车对地下结构的动力作用也相应增大，在复杂地下环境的影响下，将会出现结构和材料的缺陷或损伤[1，2]。研究表明，隧道的衬砌裂缝和渗漏水等病害现象较常出现，并且威胁着隧道内的交通质量和行车安全，同时会增加隧道结构的养护维修费用[3～5]。因此，研究地下结构损伤识别的问题越来越受到人们的重视。通过合适的方法来监测地下结构的健康状况并通过科学管养使其处于安全服役状态的研究成为近年来土木工程领域的研究热点[6，7]。在以往的研究中，国内外学者普遍将地下结构的损伤简化为该区域刚度的降低，且通常认为其质量不发生变化[8]。通过比较分析结构在损伤前后的模态参数(频率、振型等)变化，或者通过结构振动特性来分析地下结构的损伤状况[9～11]。Adams和Cawly提出采用结构的固有频率变化来对损伤位置进行识别[12]。在此基础上，Stubbs对损伤结构物理参数进行灵敏度分析，进一步验证和提高了频率识别结构损伤的有效性[13]。由结构特性可知，振型的变化较频率变化更为敏感且包含更多有用的信息，所以，West提出了模态置信准则MAC(Modal Assurance Criterion)，通过MAC置信值的大小来对结构进行损伤识别[14]。Lieven提出COMAC(Coordinate Modal Assurance Criterion)，在MAC的基础上进一步准确定位损伤的位置[15]，但该方法需要结构所有自由度的信息，在实际工程中难以应用。此外，Maia还提出使用频率响应函数曲率的频响函数来对损伤进行定位[16]，但基于频响函数的方法需要预先了解结构的输入信息，这对于复杂的土木结构来说也是十分困难的。基于以上原因，本文提出基于连续小波变换的损伤识别方法。该方法不需要提前掌握结构的基本信息和所承受荷载的大小，仅通过分析结构输出的加速度响应，即可分析判断结构损伤位置。同时，以往在进行地下结构损伤识别研究分析时，主要是通过数值分析的方法来对结构进行模拟，没有深入的结合盾构隧道自身构造特点来研究其动力特性[17～22]，因此，研究移动荷载作用下地下结构损伤识别方法及模型十分必要。本文结合盾构隧道结构试验模型，较深入地对其在移动荷载下的动力特性进行分析，并对损伤进行定位研究。通过数值算例和试验考察了不同程度损伤、多损伤下的损伤识别。同时，研究了不同位置测点对损伤识别结果的影响。

1 移动荷载作用下地下结构振动方程

Bernoulli-Euler梁认为梁对剪切变形完全刚性，只有弯曲变形，而Timoshenko梁是在Bernoulli-Euler梁的基础上，考虑了剪切变形和转动惯量。在本文中，为了更准确的模拟结构实际情况，考虑其剪切效应，将超长线状地下结构简化为粘弹性地基上的无限长Timoshenko梁，通过该简化模型提取在移动列车荷载作用下的结构响应。

1.1 Bernoulli-Euler梁模型

粘弹性地基上Bernoulli-Euler梁在简谐匀速移动荷载作用下的弯曲振动微分方程如公式(1)，其力学模型如图1所示，

(1)

式中：y为梁的竖向位移；E和I分别为截面的弹性模量和惯性矩；m，c，k分别为质量、阻尼系数和弹性地基刚度系数；P为竖向外荷载，其沿着纵向长度方向以v0匀速移动。

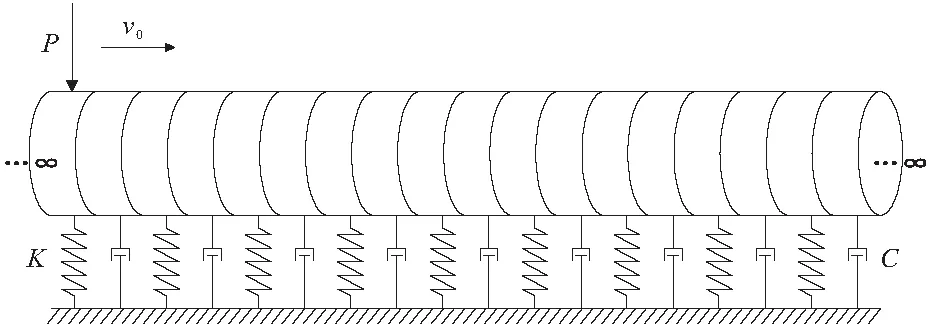
图1 单位移动荷载作用下地下结构振动分析模型

1.2 Timeshenko梁模型

在Bernoulli-Euler梁理论分析的基础上，粘弹性地基上Timoshenko梁在匀速移动定荷载P作用下的弯曲振动微分方程可写为：

(2)

式中部分参数与前式相同；y为梁的竖向位移；φ为横截面转角；G为剪切模量；A为截面面积；ξ为截面几何形状系数；ρ为截面的密度；m，c，k分别为质量、阻尼系数和弹性地基刚度系数；t为时间。竖向外荷载P沿着纵向长度方向以v0匀速移动。

2 裂缝损伤

进行结构损伤分析时，为了简化有限元建模，通常使用刚度折减的方式。这种方法假设在损伤发生时，该处只有抗弯刚度EI发生变化，质量m不变，这就忽略了损伤部位对周围未损伤单元的影响。所以，本文使用扭转弹簧的刚度变化模拟地下结构管片的裂缝损伤，如图2所示。本文模拟所采用的扭转弹簧截面均为圆形截面，且忽略弹簧扭臂变形情况，如图3所示。扭转弹簧刚度如式(3)(4)所示。

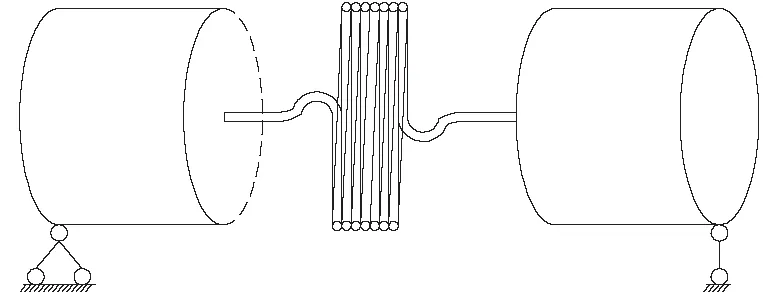
图2 裂缝损伤模型

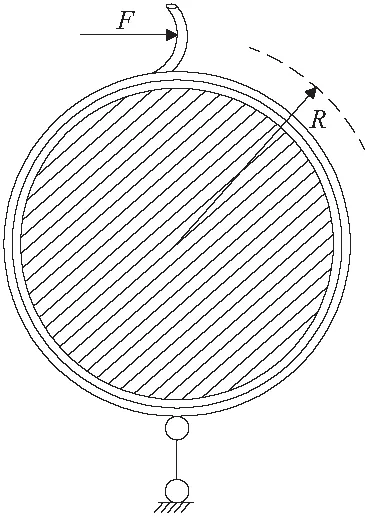
图3 忽略扭臂变形情况的扭转弹簧

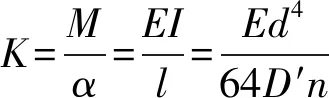
(3)

(4)

式中：D′和d分别为扭转弹簧中径和弹簧丝径；K为扭转弹簧刚度；M和α分别为扭转弹簧扭矩和扭转角度，M=FR，F和R分别为作用力及力的作用半径；l为有效长度；σ为弯曲应力；n为扭转弹簧有效圈数；Z为断面系数。

3 基于小波残余力指标的损伤识别方法

3.1 小波理论

小波变换是由法国科学家Morlet在1984年进行地震数据分析时提出[23,24]，他在分析地震波的局部时，发现传统的傅立叶变换难以达到要求，从而引入小波的概念。

小波是由一个满足条件

(5)

的函数ψ(t)，通过平移和伸缩而产生的函数簇

(6)

式中：ψ(t)称为基小波或母小波；a为伸缩因子(也称尺度因子)；b为平移因子。公式(6)称为基小波ψ(t)生成的连续小波。

设{ψa,b}为由公式(6)给出的小波函数簇，对任意函数f(t)∈L2(R)，函数f(t)的小波变换定义式为

(7)

式(7)又称为连续小波变换(Continuous wavelet transform, CWT)。

3.2 小波残余力指标

多自由度结构的振动方程如下所示

Mx″+Cx′+Kx=B·p(t)

(8)

式中：M,C,K分别为结构的质量矩阵、阻尼矩阵和刚度矩阵；x,x′,x″分别为结构的位移、速度和加速度向量；p(t)为外部激励；B为作用力定位映射矩阵。

本文对公式(8)进行二阶高斯变换，可知：

(9)

式中：s为伸缩因子(也称尺度因子)；u为平移因子，CWT为连续小波变换函数。

当结构发生损伤时，

Md=Mu-ΔM

(10)

Kd=Ku-ΔK

(11)

式中：Mu和Ku分别为未损伤状态下结构的质量矩阵和刚度矩阵；Md和Kd分别为损伤后结构的质量矩阵和刚度矩阵；ΔM和ΔK分别为由损伤引起的质量矩阵和刚度矩阵的变化。通常认为在损伤前后，结构阻尼不发生变化。

将式(10)(11)带入式(9)可得：

(12)

(13)

由于小波变换的特性，可知结构位移、速度以及加速度具有以下关系：

(14)

将式(14)带入式(13)可得：

(15)

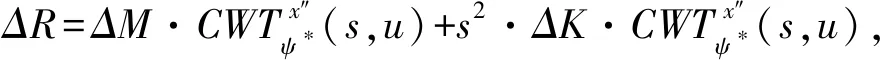
(16)

式中：ΔRu和ΔRd分别为损伤前后的小波残余力向量；σ为损伤后所有采样数据的标准偏差。

4 试验分析及讨论

根据上述整体及裂缝损伤理论模型，应用MATLAB程序编写及数值计算软件来编写相关计算程序，研究在弹性地基上，移动荷载作用下地下结构损伤识别方法。

4.1 试验设置

为验证该损伤识别方法的有效性，进行移动荷载作用下弹性地基上铝管试验。在本次试验中，弹性地基基床系数取8×106MPa/m[25]。

试验构件采用带法兰铝管，材料物理参数为：弹性模量E=2.71 GPa，泊松比为0.25，密度为ρ=7890 kg/m3，单环几何尺寸外径D1=180 mm，内径D2=160 mm，壁厚d=10 mm，长度l=140 mm，法兰处厚度d0=10 mm。采用30个单环结构通过螺栓连接，全长L=4200 mm，如图4所示。同时，制作了四种损伤构件，如图5所示，其中图5a，5b用于模拟衬砌剥落等块状损伤，图5c，5d用于模拟裂缝等条状损伤。损伤刚度分别为5%，10%，5%，10%。试验损伤构件的损伤通过刚度变化来计算，采用惯性矩I的折减来体现，梁单元刚度矩阵可表示为：

图4 试验模型

图5 损伤设置

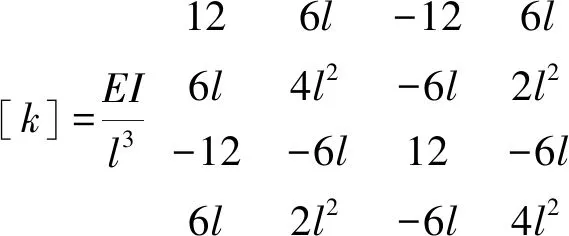
(17)

式中：l为单元长度；E为弹性模量；I为任意一般形状横截面惯性矩，其具体计算示意图如图6所示，可表示为：

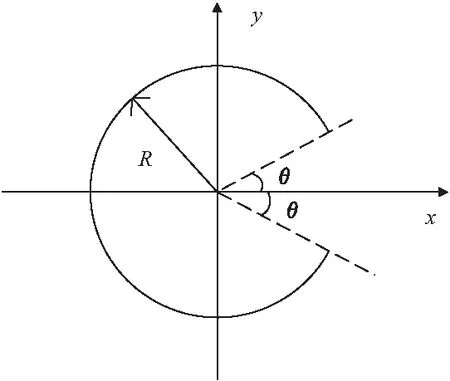
图6 惯性矩计算示意

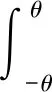
(18)

式中：R为半径；θ为损伤弧长的一半对应圆心角度。

如图7所示，以六个车厢的小车来模拟隧道结构中的移动列车荷载，每个车厢轴距为100 mm，移动荷载采用动力牵引小车装置，牵引装置能提供稳定的动力，用于提供牵引列车在缩尺隧道模型中行驶的负荷，牵引装置功率为25 W，以125 r/min的速度旋转。采样频率为1000 Hz。为了避免出现偶然误差，每个工况均测试10次。

图7 移动荷载

采用无线测试系统STS4采集软件(BDI桥梁诊断试验公司)以及8个加速度传感器来对测试结构的加速度进行采集(分别布置在2，6，10，14，18，22，25，28号铝管上)，采集仪器及加速度传感器如图8所示。其技术规格按NIST标准要求校准，如表1所示。现场采集加速度时程曲线如图9所示。

图8 无线传感装置

规格参数数值范围/g±5灵敏度/(mV/g)400频率响应/Hz0～600尺寸/mm49.5×12.4×20.3重量/grams54

图9 移动荷载作用下加速度时程曲线

试验分为无损伤、单损伤、多损伤等8个工况，具体工况如表2所示。

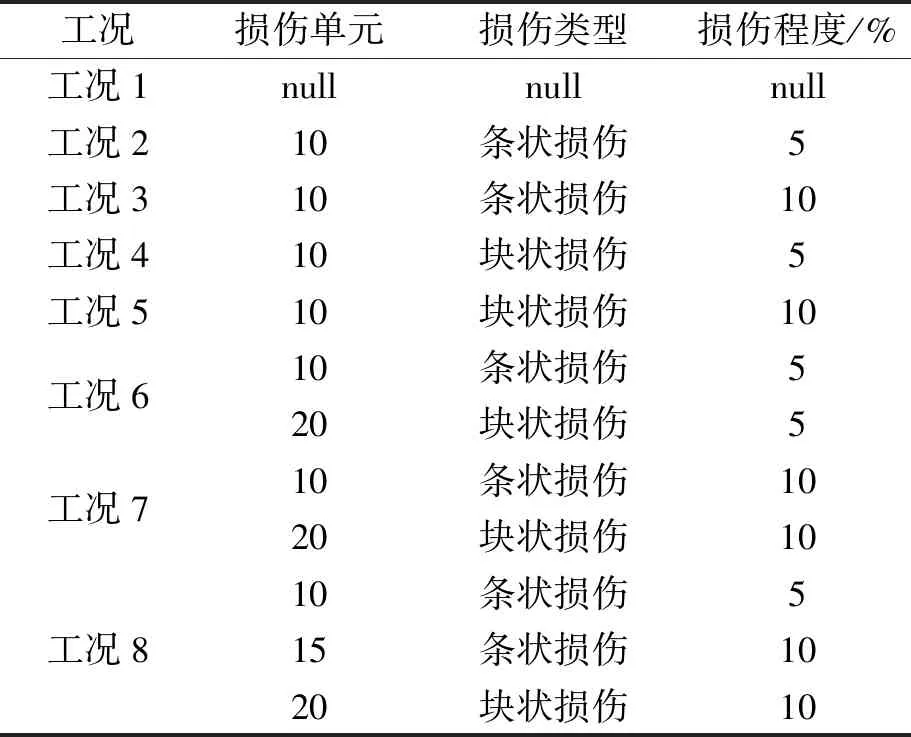
表2 损伤工况

4.2 损伤识别结果及分析

根据本文提出的方法，进行现场试验及仿真分析，对采集的加速度信号进行分析和处理，计算出了各损伤工况下不同单元的损伤识别指标值，并将仿真与试验结果进行对比。

工况1为无损状态下的损伤识别结果图，可以看到各单元损伤指标无明显放大。工况2～5的损伤设置在缩尺盾构隧道结构中第10节铝管。由图10对应结果图可看出，第10单元处损伤识别指标较其他未损伤单元有明显的放大，且随着损伤程度的增加，损伤识别指标随之增大。工况6～8为多损伤工况，由图10对应结果图可看出，设置损伤单元处损伤识别指标较其他未损伤单元有明显的放大。上述结果表明，该方法在结构损伤识别中具有有效性。

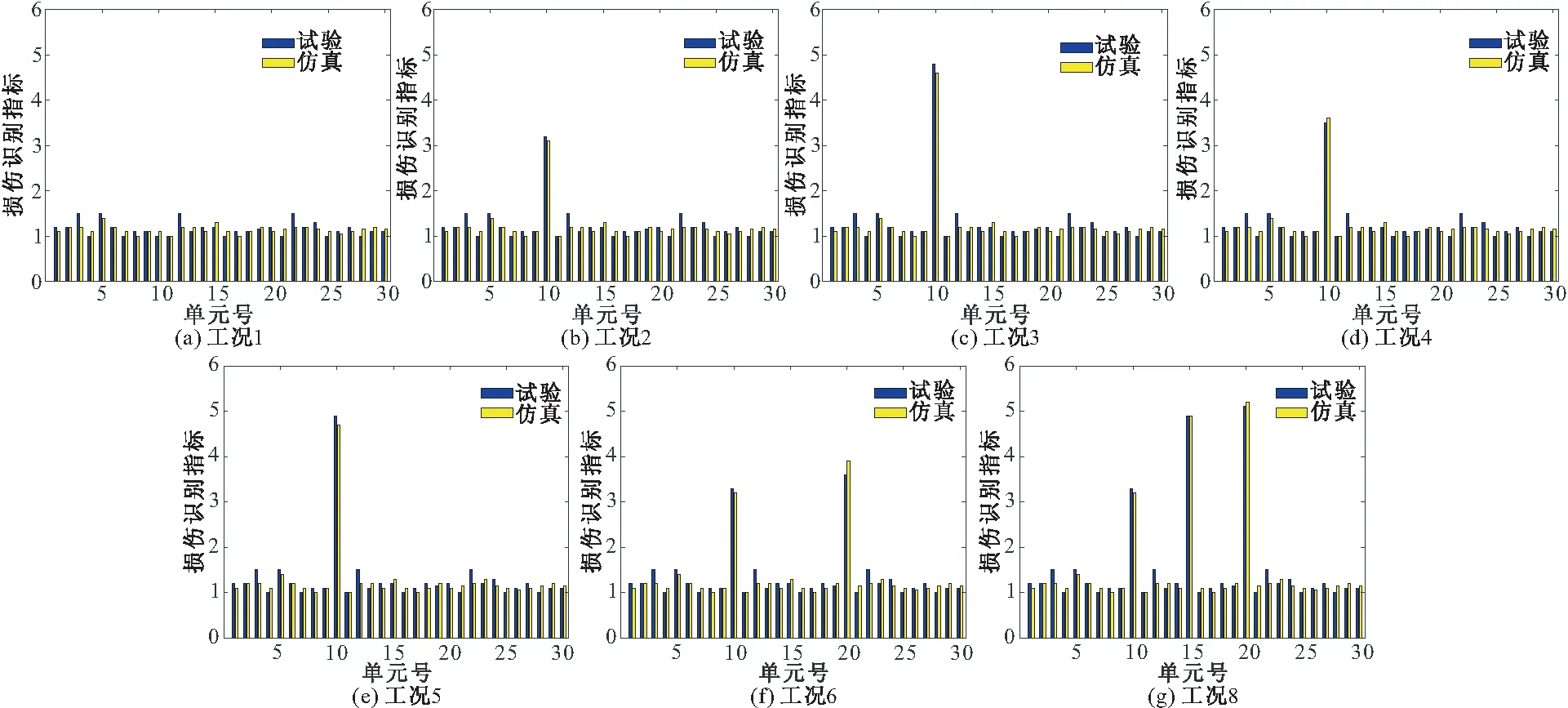
图10 移动荷载作用下各工况损伤识别结果

以工况6为例，在工况6中，第10单元(5%条状损伤)的试验及仿真损伤识别指标分别为3.3和3.2，第20单元(5%块状损伤)的试验及仿真损伤识别指标分别为3.6和3.9。而在工况2中，第10单元(5%条状损伤)的试验及仿真损伤识别指标分别为3.2和3.1，在工况4中，第10单元(5%块状损伤)的试验及仿真损伤识别指标分别为3.5和3.6，可以看出当结构具有多损伤时，各损伤单元处损伤指标与同工况单损伤时相比，损伤指标会增大，这说明各损伤单元之间相互影响。

以工况2和工况4损伤识别结果为例，工况2中，第10单元(5%条状损伤)的试验及仿真损伤识别指标分别为3.2和3.1，而工况4中，第10单元(5%块状损伤)的试验及仿真损伤识别指标分别为3.5和3.6，结果表明与条块损伤相比，当结构具有相同刚度损伤的块状损伤单元时，损伤指标较大。出现这种结果的原因应该是由于在损伤设置阶段，在两种类型的损伤刚度相对大小一致的情况下，块状损伤被切割部分面积较条状损伤大，则损伤单元质量的变化相对于条状损伤较大，这种质量的变化也可以看成是一种特殊的损伤，在一定程度上加大了刚度变化引起的结构损伤，所以损伤指标相对于条状损伤略大。