基于产品生命周期的多阶段剩余收益项目决策模型
2019-07-02王立夏
王立夏
(上海大学悉尼工商学院,上海 200899)
1 引言
项目投资决策一直以来是公司财务和投资学领域理论界和实务界重点研究与关注的内容之一。从历史发展看,相关的估值模型不断被提出,如现金流折现模型(DCF)、股利折现模型(DDM)、股利增长模型(或高登模型)等等。这些模型虽然一定程度上指导了价值评估,但由于整体上缺乏普遍适用性,所以一直备受批评----股利折现模型很难被用于不发放股利或股利稳定、股利不随公司业绩变化的股票估值;现金流折现模型则很难适用于因公司发展而现金流为负的成长型企业;对比定价如市盈率估值法等则在理论上缺乏可靠依据[1]。
Edwards和Bell[2]在股利折现模型的基础上提出了剩余收益模型(RIM),该模型一提出就引起了学者们的广泛兴趣。剩余收益模型可以作为公司权益价值的有效估值模型并已经获得金融与财务会计理论界和实务界的广泛认可。Feltham和Ohlson[3-5]基于净剩余关系和线性信息动态假说构建了三个经典的剩余收益模型,简称Feltham和Ohlson系列剩余收益模型或Ohlson系列剩余收益模型。王立夏[6]认为该系列模型堪称经典是因为它有效对接了会计信息,为会计信息有用提供了实证的理论依据。国内外金融与财务会计学者对剩余收益模型进行了大量的后续研究,主要集中在以下两个方面:
一方面是关于剩余收益模型的应用与比较研究。王天东等[7]通过实证发现在盈利状态和亏损状态、不同信息质量以及不同规模情况下剩余收益估值模型的适用性存在显著差异,成长性也是影响剩余收益估值模型的因素,同时净资产账面价值和剩余收益都具有价值相关性,且互有增量价值相关性。廖俭[8]则通过理论与实务比较了剩余收益估值模型与自由现金流量估值模型,并得出剩余收益估值模型优于自由现金流量估值模型的结论。林海宁和马群[9]指出将会计信息与公司价值相结合的剩余收益模型对股票价格和公司价值的解释力最强,充分利用具有较高参考价值和公信力的会计数据是剩余收益模型的突出优势。
另一方面是关于剩余收益模型的改进研究。张启銮和刘倩倩[10]通过引进杜邦分析体系,对Ohlson收益模型进行改进并选择房地产行业进行了实证分析。王立夏[11]基于市场风险因素构建了风险因子调整的剩余收益模型(RIM-σ2)。敖诗文和高雅[12]则通过引入预测期末市净率(Pn/ BVn) 对股权价格进行预测,使原模型变为有限期的预测模型。王琳[13]构建了行业价值倍数,即行业中加权综合估值倍数对剩余收益模型进行改进,并以案例形式研究三家建筑公司来验证所改进模型的合理性与有效性。
可以发现,剩余收益模型主要是用于公司权益价值的评估,并且Ohlson系列剩余收益模型完美地对接了会计历史信息。由此引发问题:剩余收益模型是否可以像自由现金流折现模型、股利折现模型等估值模型那样用于对项目的投资决策?是否可以运用常用的如净现值(NPV)等方法来计算投资价值?计算投资价值时需要哪些数据,该如何进行评估决策?
本文借鉴甘柳等[14]、李珠瑞等[15]的模型构建方法,基于产品生命周期理论,对剩余收益模型进行拓展研究,从理论上构建基于产品生命周期的多阶段剩余收益项目投资决策模型,并进一步地对所构建的模型进行管理运用与数据赋值检验研究。
2 理论基础
2.1 剩余收益模型理论基础
我们知道,股利折现模型的一般表达式为:
(1)
式中:Vt表示第t期项目权益市场价值;Et[dt+k]表示人们预期第t+k期间将要收到的股利期望;rt+j表示t+j期间的贴现率。
Edwards E O和P W.在上式(1)的基础上,根据剩余收益的定义,得到如下剩余收益模型表达式[2]:
(2)
式中:BVt表示项目在第t期末的净资产账面价值;r表示无风险利率;Xt+τ表示项目在第t+τ期的净利润;Xt+τ-rBVt+τ-1表示第t+τ期的超常剩余收益(又称剩余收益)。
由式(2)可以看出:根据该剩余收益模型,公司权益价值最终由该公司当期净资产账面价值、未来各期的剩余收益(或预期净利润和净资产)以及贴现资金成本率(或贴现率)决定。为了计算公司内在权益价值,我们不需要预测公司未来支付给股东的股利,而只需要对未来的收益和净账面价值进行预测。
由于该模型涉及到未来无限期的剩余收益的折现求和,使得估值的计算存在困难。由此Feltham和Ohlson提出线性信息动态关系的假设,得到如下剩余收益模型(3):
Xt+1=αXt+υt+1+ε1t+1
υt+1=βυt+ε2t+1
(3)
式中:Xt+τ表示第t+τ期的剩余收益;υ表示影响剩余收益的其他因素;ε1、ε2表示均值为零的随机变量;Rf表示折现率;α、β为相应变量因素的系数,为已知常数;
其他字母表示的意思同上。
式(3)通过对模型(式(2))中的剩余收益加入线性信息动态条件,使得未来收益和净账面价值等会计数据具有一定的规律性,从而可以用本期的会计数据来预测未来的会计数据,由此解决了项目未来会计数据无法直接获得的问题。
2.2 产品生命周期发展理论基础
Dean[16]首次提出了产品生命周期的概念,他认为根据产品在市场中的逐渐演化过程,可以将产品划分为推广、成长、成熟和衰亡四个阶段,不同的阶段产品的定位不同。而美国哈佛大学教授Vernon R[17]则从生命周期视角研究产品发展过程中的阶段性问题,形成了著名的产品生命周期理论:产品生命周期(product life cycle,简称PLC),是指产品的市场寿命,即一种产品进入市场后,它的销售量和利润都会随时间推移而改变,呈现一个由少到多再由多到少的过程,就如同人的生命一样,由诞生、成长到成熟,最终走向衰亡,这就是产品的生命周期现象。该理论广泛运用于企业的产品开发和项目决策,已经成为了一门非常重要的科学,并广泛运用于管理科学相关领域。美国Booz Allen & Hamilton[18]基于市场销售变化规律角度研究将产品生命周期分为为进入期、成长期、成熟期和衰退期(见图1)。Gort和Klepper[19]则在定性和定量分析产品生命周期的基础上对内生型产业生命周期的演化进行了相关研究,根据产业中的厂商数量将产业划分为引入期、大量进入期、稳定期、大量退出期和成熟期五个阶段,建立了产业经济学意义上的第一个产业生命周期模型——G-K模型。
万君康[20]将不同的产品生命周期理论基于研究的出发点及应用重点等方面的区别总结如下(表1):
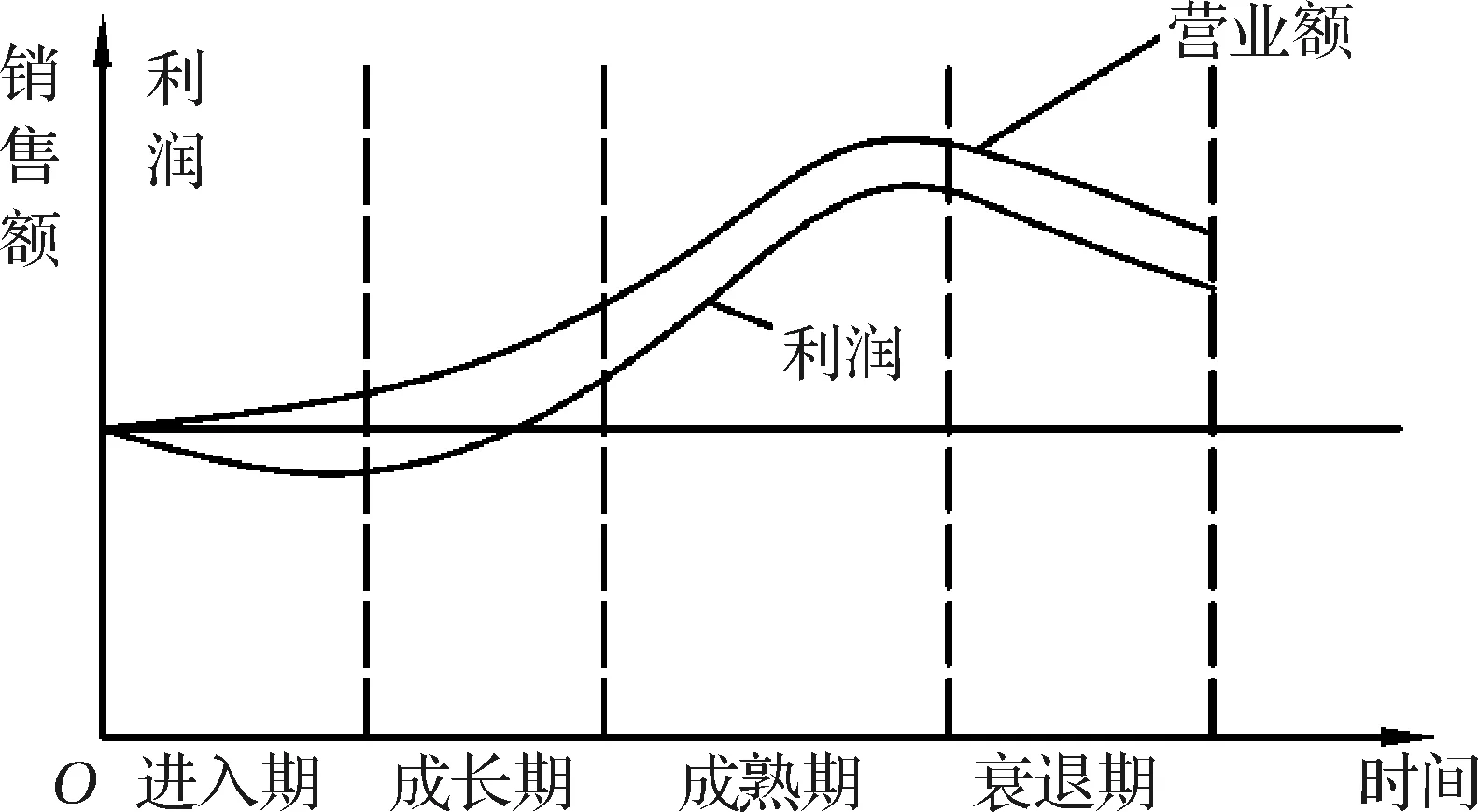
图1 产品生命周期模型
由于产品生命周期理论发展比较早,至今已相对成熟,产品生命周期可以分为四个阶段已形成共识。本文将产品的生命周期分为投入期、成长期、成熟期和衰退期这四个周期。
2.3 研究基础
首先,剩余收益估值模型和产品生命周期理论均为发展成熟的理论,在各自领域均已获得学者们的广泛共识。但两理论的结合研究,至今则显得比较匮乏。

表1 不同角度产品生命周期理论的区别表
其次,剩余收益估值模型对公司权益价值评估时是基于公司净资产及其所产生的超常剩余收益。同样地,项目投资决策也是基于其未来的投资收益和现时的投资支出。两者具有共性,如果把一个投资项目当作一个公司,那么剩余收益估值模型理论也可以用于项目价值评估。
最后,剩余收益估值模型对公司权益价值估值时是假设公司是持续或永续经营的,这也是Feltham和Ohlson系列收益模型中提出的线性信息动态关系假设的基础。项目投资则不可能持续或永续,其一般都具有有限的持续期。并且项目投资具有明显的产品生命周期特性。
鉴于此,本文拟从经营管理学的学科范畴展开,在剩余收益模型的基础上,基于上图1所述的产品生命周期及其各阶段的不同特征,力图构建更能反映产品各个发展阶段特征的多阶段剩余收益项目决策模型。
3 模型的构建
3.1 一般型模型构建
根据上述剩余收益模型以及产品生命周期的理论基础,项目的价值可以根据其四个不同发展阶段分别进行估算:
第一阶段,即投入期,就是项目在当期t时刻的价值,由于此时项目未来的价值尚未体现,故其真正的价值就是其实际投资,也就是项目实际投资的账面净资产。
第二阶段,即成长期,是指自t+1时刻项目开始运营到未来的第m年,这一阶段的产品经营状况属于成长阶段,其收益具有高速增长的特征。
第三阶段,即成熟期,是指自第m+1时刻项目运营到未来的第n年,这一阶段的产品经营状况属于相对稳定,其收益的波动比较小,具有在一定区间幅度内波动的特征。
第四阶段,即衰退期,是指自第n+1时刻开始到项目结束或退出期(第ξ期),这一阶段的产品经营状况处于衰退期,其收益逐年变小,直至项目结束经营或更新换代(转换至下一个生命周期,另行重新开始)。
基于上述分析,假设每年的折现率均为R,则可以对一般剩余收益模型(式2)进行分解,便得到:
(4)
式(4)就是本文提出的基于产品生命周期的多阶段剩余收益项目决策模型的一般表达式。即项目的价值主要由以下四部分组成:
(1)BVt:企业现有项目投入的账面价值,它代表项目投资所积累的在t时刻的价值。本文称之为第一阶段的价值,记V1;
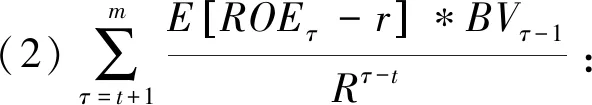
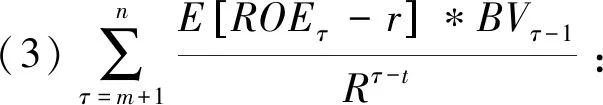
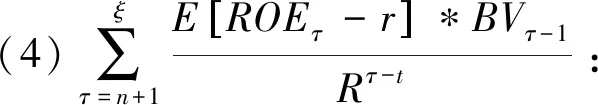
由此,项目的累计投资价值现值为:Vt=V1+V2+V3+V4。
3.2 运用型模型构建
很显然,上述多阶段剩余收益项目决策模型(式(4))的一般表达式对项目价值进行估值的实用性较差,因为式(4)的多阶段剩余收益模型四个阶段中,企业的发展速度和特征均是不同的,其各阶段的投资回报率(ROE)应该是具有反映产品生命周期的阶段性特征,但一般表达式的模型中却未能具体反映。基于此,本文就此进一步研究,以构建运用型的项目定价估值模型。
3.2.1 定义及假设条件
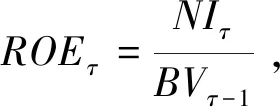
式中:ROEτ表示第τ期的净资产回报率;NIτ表示第τ期的净利润;BVτ-1表示第τ-1期期末的净资产账面值。
同时,本文拟提出如下假设前提:
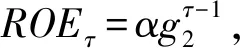
该假设的合理性在于:一方面,Kang和Kim[21]以及李娜等[22]总结了七种具有代表性的经济与管理常设函数:幂函数、指数函数、HARA函数、对数函数、幂函数复合函数、线性函数、指数函数复合函数;同时,郭凯明等[23]用指数函数来假设企业家精神和经济的增长。另一方面,根据产品生命周期的特征,产品在这个阶段属于成长期,其收益是随着时间(年份)持续增长的,故其ROE也是持续增加,因而适合递增的指数函数,但由于各产品不同以及其他因素的影响,故增加一个调整系数α。
假设(2),在第三阶段,即从m+1年开始到第n年的成熟期,项目的剩余收益符合Feltham-Ohlson剩余模型收益中的线性信息动态关系假设。即在该阶段,相邻两期的剩余收益存在一定的线性关系。很显然,该阶段的净资产回报率会在一定的区间幅度内波动,符合Feltham-Ohlson所提出的相邻两期存在线性动态关系的假说。
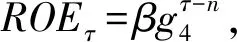
该假设的合理性类似于假设(1),但由于该阶段的产品收益是递减的,故适合递减的指数函数,同样道理,基于产品的不同以及其他因素的影响,增加一个调整系数β。
假设4,不考虑项目中途的现金分红、或其他方式的收回或减少投资
3.2.2 运用型模型的推理与分析
基于上述多阶段剩余收益项目决策模型的一般表达式(式(4)),根据产品生命周期理论及上述假设,现在针对每一阶段的价值分别进行推理与分析。
(1)第一阶段价值V1,很显然,由于项目尚属于投入阶段,该阶段的项目价值就是V1=BVt。
(2)第二阶段价值V2
根据式(4),可以知道该成长期的价值为:
根据假设1,由于:

V2
(5)
式中:BVτ表示第一阶段期末或第二阶段期初的账面净资产值;V2表示第二阶段折现到第t期的价值,即第二阶段的价值;其他字母代表的意思同上。
(3)第三阶段价值V3
根据式(4),可以知道该成熟期的价值为:
根据假设2,上式可以转变为:
Xτ+1=φXτ+υτ+1+ε1τ+1
υτ+1=φυτ+ε2τ+1
(6)
将式(6)展开并整理可得:
V3
(7)
其中:0<φ,φ<1
式中:Xm、Xn分别表示该阶段期初和期末(即第二阶段的期末、第四阶段的期初)的剩余收益;υm表示影响期初剩余收益的其他因素;φ、φ分别表示剩余收益和其他因素变量的系数,为已知参数;其他字母表示的意思同上。
(4)第四阶段价值V4
根据式(4),可以知道该衰退期的价值为:
V4
(8)
式中:BVn表示第三阶段期末或第四阶段期初的账面净资产值;其他字母代表的意思同上。
3.2.3 多阶段剩余收益模型
在多阶段剩余收益项目决策模型一般表达式(式4)的基础上,基于上述假设(1)至假设(4),可以得到如下实证型多阶段剩余收益定价模型:
Vt=BVt
(9)
且:
Xτ+1=φXτ+υτ+1+ε1τ+1当τ∈(m+1,n)
υτ+1=φυτ+ε2τ+1
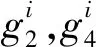
3.3 考虑分红的多阶段剩余收益模型
本文中提出的假设(4)对项目来说是一种推理的特例,现在由特殊到一般,必须考虑项目的分红(包括每年固定的投资回收)现实,如现在流行的PPP项目,资金提供方每年从项目收回一定固定比例的收益。由此,针对本文中的假设(4)替换成如下假设(5)。
假设(5):项目在每一期的分红比例为Ω,即每期的分红金额为NIτΩ,则留存净利润为NIτ(1-Ω)。
由假设(5),很容易知道:
由此,在上式(9)的基础上考虑项目分红的多阶段剩余收益模型可以表示为:
(10)
式中:Ω表示项目净利润的分红比例;其他字母所代表的意义同上。
4 拓展性研究
4.1 成熟阶段的行业平均回报率
上式(9)和式(10)的多阶段剩余收益定价模型虽然针对产品的生命周期不同特征来计算各周期的价值,但仍没有离开Feltham-Ohlson系列剩余收益模型中的线性信息动态关系假设,即在本文的假设(2)中,针对第三阶段的剩余收益价值,在该成熟阶段仍然假设产品各年的剩余收益满足线性信息动态假设。
事实上,当产品在步入成熟期时,经过前期的投入并获得超额回报率后,其净资产回报率将会趋向于行业平均回报率。由此,我们针对第三阶段,可以将假设(2)修改为:
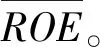
由此,企业第三阶段的价值和总体权益价值将分别变为:
4.1.1 不考虑项目分红
项目在第三阶段,即成熟期的价值为:
(11)
相应地,项目的价值为:
Vt=BVt
(12)
同时:
4.1.2 考虑项目分红
项目在第三阶段,即成熟期的价值为:
(13)
相应地,项目的价值为:
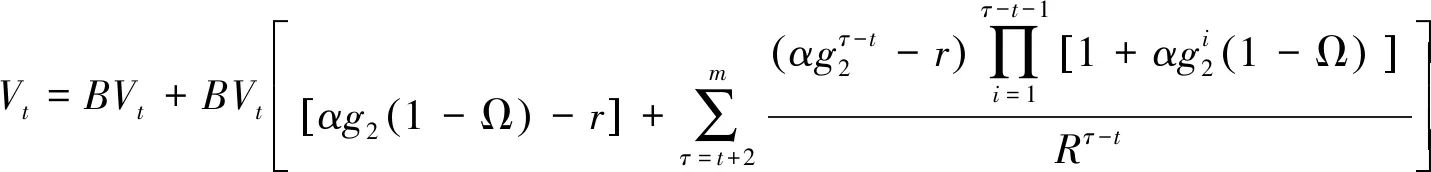
(14)
同时:
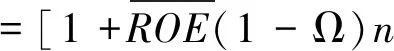
4.2 项目的价值最大化
从上述有关项目的价值模型中,很容易发现,随着时间的推移,项目的价值会越来越大,然而,其是否会无限的增长呢?很显然,项目价值不可能无限增长,当其价值增大到某种程度后应该会下降,故在产品的生命周期中,项目的价值应该是先上升后下降的关系,即下图的关系(见图2):
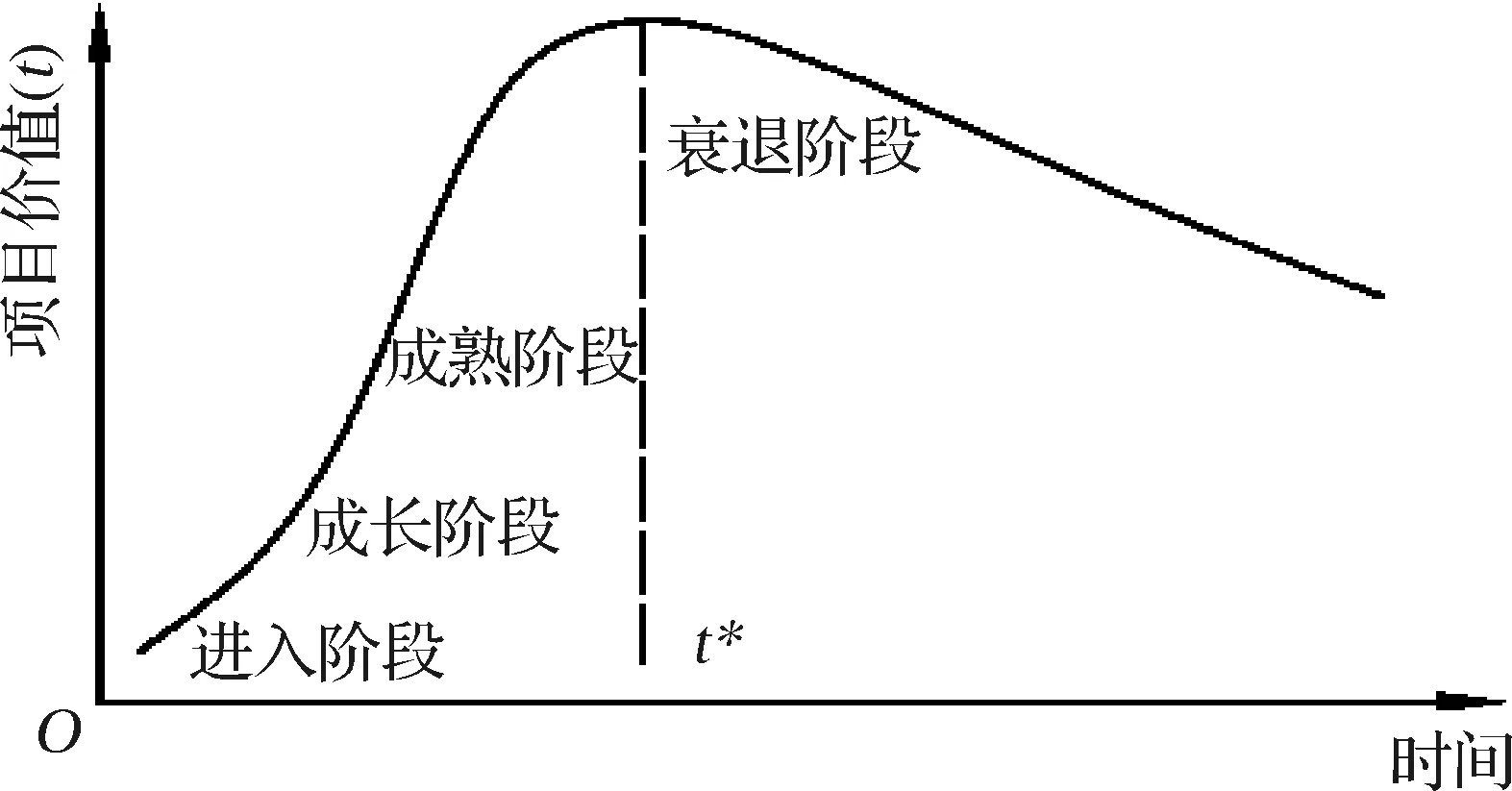
图2 产品生命周期的价值体系图
那么,什么时候是项目价值最大化的时刻呢?
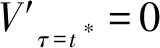
可以得到:
(15)
式(15)得出的结果非常符合常识,即当项目的净资产回报率等于无风险利率时(时刻),项目的价值达到最大。超过该时刻,则项目的价值将越来越小。此时,投资者要么将产品升级换代,重新进入另外一个产品生命周期,要么将终止该项目,重新投资于另外一个新的项目。否则,从经济及理性的角度,原产品继续经营对投资者来说是不经济的,某种程度说,也是一种资源的浪费。
正因为如此,本文的下列项目决策与分析及数值实验均是基于净资产回报率大于等于无风险回报率,这也符合现实,从理性的角度考虑,当净资产的回报率低于无风险回报率时,决策者应终止该项目运营。
5 项目决策与分析
不考虑项目分红或投资者在产品经营过程中收回投资的情况下,利用NPV方法,则可以对该项目做出正确的决策,即:
NPV=Vt-It
It为项目的投资额,很显然,不管投资期(建设期)是多长时间,均存在It=BVt,由此:
NPV=BVt
即:
NPV
(16)
很显然,当式(16)中的NPV≥0时,该项目投资是可行的;当NPV<0时,该目投资是不可行的。
同时,在净资产回报率均大于等于无风险回报率的情况下,从式(16)很容易发现:当m越大时,则NPV越大;同样地,当n越大,NPV也越大。
6 数值实验
借鉴李春好等[24]、周忠宝等[25]和李美娟等[26]等模拟验证分析方法,基于实务考量,模型(式(12)或式(14))中相关参数的理论取值范围如下(见表2):

表2 参数的理论取值范围
假设BVt=1,r=5%,即R=1.05,系数α和β均取值0.3,并且不考虑分红,即的情况下,其他各参数的不同取值与多阶段剩余收益的项目决策计算表如下(见表3):
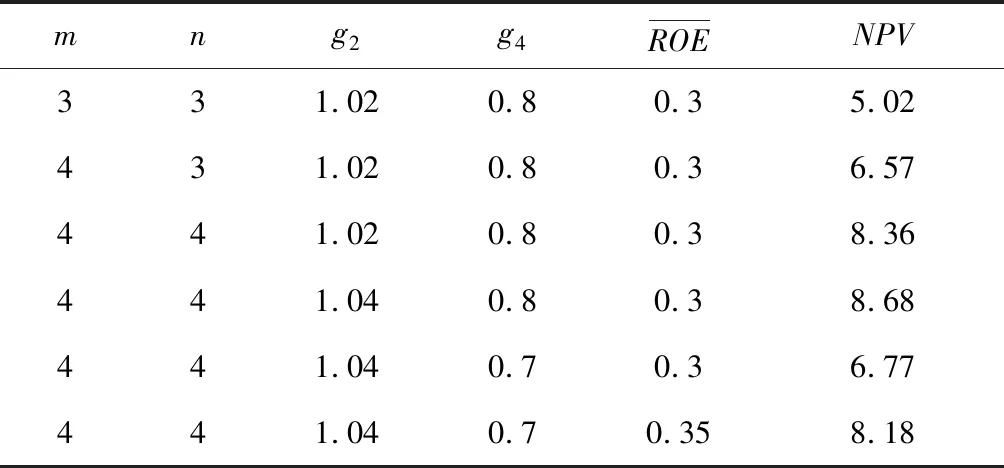
表3 NPV计算表
从表3可以发现,当产品所处生命周期的增长期(m)越长,其NPV越大,符合推论1;同样地,当产品所处生命周期的成熟期(n)越长,其NPV也越大,符合推论2。还可以进一步发现,当产品所处生命周期的增长期时,其增长率(g2)越高,NPV越大;当处于生命周期的衰退期时,其下降率(g4)越快,NPV就越小。最后,当产品所处生命周期的成熟期,其平均回报率越高,则其NPV也越大。
同时,如果改变系数和的取值,其结果保持与表3同样的变化趋势。
7 结语
本文在剩余收益模型的基础上,引入产品生命周期理论,从理论上构建了多阶段剩余收益项目决策模型,通过对模型的逻辑推导、运用分析和赋值检验,结果表明新构建的模型可以作为一种项目投资决策评估模型。本文的主要贡献表现在:
第一,拓展了剩余收益模型的应用。剩余收益模型主要是用于对公司权益价值进行估值,而Ohlson系列收益模型则有效地将其与会计信息有用观完美结合,极大地有利于会计的实证研究。本文则将其扩展到项目投资决策,并运用成熟的产品生命周期理论构建剩余收益项目决策模型,通过赋值分析并检验了该模型的可行性。
第二,有效解决了剩余收益模型中存在的无穷项问题。由于项目具有生命周期特征,故其存在一定的有限期间,或者根据价值最大化选择确定的经济运行期间,进而不存在一般剩余收益中存在的无穷项问题。《企业进入创新活跃期:来自中国企业创新动向指数的报告——2016·中国企业家成长与发展专题调查报告》[27]指出,在经济高速发展的当今,产品的生命周期将越来越短。本文的研究符合产品生命周期有限的现实,并不需要设定项目无限期发展或增长这一不太符合实际的假设。
第三,有利于寻求项目投资决策时的价值最大化。之前的众多项目投资决策模型均只是计算出项目的投资价值(如NPV),而未能深入分析了解项目存在最大化的时刻。而根据本文构建的剩余收益项目决策模型则可以计算出项目最大化的时点(t*)。另一方,根据本文所构建的模型,有利于投资人对项目投资进行深入分析并作出正确的决策。
一是尽量投资成长期高(g2)且持续时间长(m)的项目或产品。这就要求决策者选择发展前景好,进入壁垒高的项目或产品进行投资。
三是选择衰退期相对慢的项目或产品。这也要求决策者选择不会被马上替代的项目或产品,这样可以最大限度地获得剩余价值,增加投资收益。
