基于需求预测和模块化的应急物资库库联动方法研究

魏宇琪，杨 敏，梁 樑

(合肥工业大学管理学院，安徽 合肥 230009)

1 引言

中国是世界上遭受自然灾害影响最严重的国家之一，近几十年中特大地质灾害和气象灾害等(如汶川地震和2008年特大低温雨雪冰冻灾害等)频频发生。为了降低自然灾害对人民群众的生命财产安全造成的威胁，应急物资储备体系和理论建设的加强和完善成为了我国政府和应急管理学术界的重点工作任务。

在应急预储体系建设方面，我国政府为了保障受灾群众基本生活、维护社会和谐稳定，正逐步加强应急物资储备体系建设。目前我国应急物资储备体系建设已经取得较大成效，初步形成“中央-省-市-县”四级应急物资储备体系，但与日益复杂严峻的灾害形势和社会各界对减灾救灾工作的实际需求和期望效果相比，应急物资储备体系建设还存在一些共性问题：1)由于我国目前的实物储备模式所采用的(t,S)库存策略导致的无法依据自然灾害趋势预测意见和灾害实际发生情况进行动态调整等问题[1-2]；2)由于缺乏成熟的跨区域间应急联动合作模式所导致的储备物资流动性较差和物资闲置损耗较大等问题[2]；3)由于缺乏成熟的应急物资模块化预储和调度模式所导致的预储和调度中的物资不配套等问题[3-4]。

为了全面加强救灾物资储备体系建设，妥善解决应急物资储备体系中存在的问题，提高国家整体救灾应急保障能力，我国民政部等九部门于2015年8月31日联合印发了《关于加强自然灾害救助物资储备体系建设的指导意见》(以下简称《指导意见》)，并在该意见中对应急物资储备体系建设提出了一系列任务，其中包括：建立救灾物资紧急调运应急联动机制并完善跨区域救灾物资援助机制、根据自然灾害趋势预测意见和灾害实际发生情况做好救灾物资应急储备工作等。

在应急预储理论研究方面，应急管理学术界针对我国目前主要的三种物资预储形式[2](实物预储、协议代储和生产能力代储)分别进行了物资存储模式和物资最优预储量的研究。其中针对实物储备模式的主要研究如下：赵黎明等[5]将应急物资储备模式分为常规储备和非常规储备，并建立模型分别计算一定情况下两种存储模式下的最优物资存储量；姚令侃等[6]将应急物资中的防洪抢险物资储备看做一种信息不完全型决策问题，提出用于确定每年度防灾物资储备粮的概率排序型决策模型；吕涛和聂锐[7]在应急煤炭储备方面从消费量、自给率、运输条件、经济实力4个方面分析影响储备规模的因素，测算各省区的储备规模；秦军昌和王刊良[8]将应急物资的需求按照需求时间划分为响应期需求和恢复期需求，针对两个需求阶段不同的特点构建了基于跨期一体化的最优订货量单周期库存模型；郭晓光和张晓东[9]将具有不确定性的应急需求考虑为一种随机需求，研究了区域库存总量和节点库库存分量的决定模型。李维等[10]在对突发性自然灾害应急物资储备影响因素的调查和分析的基础上，运用需求理论、库存理论和多目标决策等理论，对基于情景的不同自然灾害下的物资储备水平进行了研究。

在协议代储和生产能力代储方面，包玉梅[11]构建了应急实物储备和协议储备两种模式协同的一种二级储备模型；丁斌等[12-14]从合作博弈和政企合作的角度进行了政府与供应商合作进行的应急物资储备策略研究。张自立等[15]研究了政府在应对突发事件时，应当如何激励生产企业增加产量，以及运用行政手段和市场手段调节企业的生产能力储备等。

上述文献从不同的角度出发，对应急物资的最优预储模式和期初预储数量进行了研究：第一类研究从强经济性的角度，以物资过剩引起的经济损失和物资短缺引起的社会损失最小为目标(如姚令侃等[6])求解最优库存量；第二类研究从弱经济型的角度将灾民的救灾需求放在首位，在满足一定应急物资保障水平的条件下以成本最小为目标(如郭晓光和张晓东[9])求解最优库存量。

然而，上述研究尚有待完善之处。第一，上述研究均没有考虑到不同种类的应急物资之间可能存在的固定使用搭配关系。根据《应急保障物资分类及产品目录》的分类标准，国家发改委把应急保障物资分成了防护用品、生命救助、生命支持、救援运载、临时住宿、污染清理、动力燃料、工程设备、工程材料、器材工具、照明设备、通信广播、交通工具等13类。国内学者对这13类物资进行了进一步的归类。张旭凤[16]按应急物资使用的优先级别将应急物资分为4类，即生命救助物资、工程保障物资、工程建设物资、灾后重建物资；张永领[17]按照突发事件的应急管理阶段和主要应对环节将应急物资分为应急处置物资、基础保障物资和恢复重建类物资；王宗喜和阳波[18]按应急需求将应急物资分为灾民生活需求物资、抢救物资和灾后初期重建物资等三类。张永领[19]通过模糊聚类方法，将应急物资划分为七个物资种类。与之对应的，一些研究认为，对于某些种类的应急物资，如军事物资和医疗物资，其在存储和运输的过程中，存在着模块化(单元化)物资的概念[20-23]。这些物资之间存在着一定程度的依赖关系，它们之间往往需要共同协作才能够完成某项工作或满足某种需求，且它们之间通常存在着固定的比例关系。在本文中，我们参考了文献[22-23]对应急物资模块给出如下定义：应急物资模块是由具有一定数量比例关系的装备或物资组成的具有特定应急功能的集合体。而我们在上文中提到的相关应急预储理论研究都没有考虑到应急物资的这种模块化性质。

为了便于研究，我们将应急物资的模块化进一步分为两类：一类是物理模块化，即将需配合使用的应急物资按照一定的数量比例打包为实体的应急物资模块，如急救包等。已经被物理模块化的应急物资可以被看做为“一种”应急物资，可以在预储和调度中按照普通应急物资对待。二是数量关系模块化。这类应急物资模块中的物资既需要按照一定的数量比例关系进行搭配使用，又因为安全或储存条件等原因而不能被打包。对于此类模块化物资，我们在预储和调度过程中就要注意保持其预储数量比例关系在调整结束后符合要求。

第二，上述研究均没有考虑应急物资的时效性，即没有考虑应急物资的有效使用周期对物资使用价值的影响。物资在有效期限内被使用是该物资的最大价值体现，而物资闲置失效则会导致物资价值大幅度降低，甚至为零或负数。因此，通过考虑物资时效性，可以在物资失效前通过物资轮转实现其价值提升。

第三，上述研究均没有考虑到在订货周期内[1]当应急需求预测发生大幅度变化时调整预储水平的具体措施(我国救灾物资储备的采购周期为一年)。最后，上述文献均没有对《指导意见》所提出的救灾物资紧急调运应急联动机制和完善跨区域救灾物资援助机制进行研究。即上述研究无法通过对不同区域中的应急仓库之间的物资进行轮转调运来降低物资损耗成本和应对物资需求。

基于以上考虑，为了响应《指导意见》对应急预储研究工作的要求、更好的应对不确定的应急物资需求以及减少应急物资短缺导致的救灾损失与应急物资积压所导致的经济成本，本研究拟建立一种应急物资的预储调整与跨区域轮转机制：在目标地区内各区域应急物资需求分布已知的前提下，通过跨区域的物资轮转和其他物资补充方式对各区域物资预储数量进行调整，以尽量满足目标区域内即将发生的物资需求；同时，通过对物资补充方式和物资轮转路线的优化选择，尽可能的降低应急预储调整的成本，并合理利用区域内的已存储物资，降低物资损耗，使其价值得以最大发挥。为简短起见，在下文中这种应急物资的预储与轮转机制也被称为库库联动机制。

2 基于物资需求预测的库库联动机制模型构建

2.1 数学描述和假设

本文以一个区域内的由若干应急物资储备库组成的应急预储网络为背景，假设该网络受控于统一的指挥中心，以尽量减少未来可能发生的灾害所造成的人民群众生命财产损失为目标，并在此基础上降低预储成本。为了更好的达到这个目标，应急指挥中心在灾害发生之前所面临的决策问题就可以表达如下：如何根据未来一段时间内的应急物资需求分布预测对地区内各储备库的应急物资预储数量进行调整，以便更好的满足物资需求并尽量降低预储成本。

我们对上述决策问题给出如下数学描述：

1)T：[t0,t1]表示预储调整决策问题的目标时间区间和需求预测信息的目标时间区间。

2)W1,…,WM表示目标地区中负责不同区域应急物资预储的M个应急物资储备库，Wj表示第j个储备库。

3)Ljj′表示Wj与Wj′之间的距离，c1 表示单位车辆载货运输单位距离的运费，c2表示单位车辆空车机动单位距离的费用，c0表示单位车辆的租赁成本。

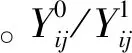
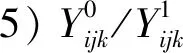
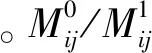
7)Aij/Acj表示Wj在T上针对Yi/Mc可能发生的需求数量aij/acj的集合：Aij={aij|pija>0}/Acj={acj|pcja>0}(pija/pcja表示在T上，Wj对Yi/Mc的实际需求为a的概率)。

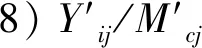
9)ΔYijm表示Wj在市场上购买的Yi的数量，Vijm为Wj购买的Yi的市场价格。

10)ΔYij′j表示从Wj′调运到Wj的Yi的数量，ΔYij′jk表示其中将要在T内到期的Yi数量。值得说明的是，ΔYij′jk是包含在 ΔYij′j之中的。

此外，为了方便建模分析预储调整决策问题，我们给出如下假设：

2)假设灾前物资预储调整行动是以在一定保障度即一定可能性下满足区域内各应急仓库覆盖地区的物资需求为约束，同时以预储成本最小为目标。

3)假设仓库之间具有同质性，即任一仓库所存储的物资都可以被转存至另一任意仓库，且仓库的存储空间没有上限。

4)假设应急物资预储水平的调节手段有两种：(a)通过区域内已有应急物资在不同仓库之间的再分配对各应急仓库的预储水平进行调节；(b)通过市场购买对区域内各应急仓库的预储水平进行补充。

5)假设物资调运的载体为同质的运输车辆，且各应急物资储备库之间的物资运输所造成的成本基于运输距离。

6)假设应急物资储备库中所存储的应急物资都是离散的。此外，我们假设单位车辆所能装载的Yi的数量为li。为方便起见，在下文中我们将以li(即单位车辆装载量)为最小单位对Yi进行运输、购买。

7)目前主流的资源配置研究对于资源调度时间有两种处理方式：1)将调度时间作为多目标优化中的一个目标[24]；2)忽略调度时间[25]。由于本文的研究对象是应急物资预储的灾前调整，所以我们假设各物资储备库之间的物资调运有较为充足的时间(我国代储单位接到民政部调拨通知后，应在36小时内完成储备物资发运工作[1])开展进行，故在本文中不将物资调运时间作为优化目标。

在此我们对于假设2，也就是预储调整问题的目标设定做出解释和展开讨论。由于灾害所具有的不确定性，决策者很难通过预储一定量的物资来保证物资需求的绝对满足。其次，由于灾害的等级越高其发生的概率也就越低(秦军昌和王刊良[8]、郭晓光和张晓东[9])，决策者也不会为了满足所有可能性下的需求去预备足量的物资。所以在本文中，我们假设预储调整工作的目标是在一定可能性下满足区域内各应急仓库覆盖地区的物资需求。

s.t.

(1.1)

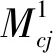
s.t.

(1.2)

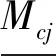
2.2 模型构建

首先我们考虑经过物资调运和物资购买过程之后，仓库Wj所预储的物资Yi的存量状态。

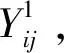
然后我们考虑预储调整活动中可能发生的成本和收益。我们假设可能存在的成本有两种：由物资转运带来的运输成本CT以及物资购买带来的购买成本CB；假设可能存在的收益有一种：由物资轮转带来的物资期望使用价值增加量 ΔE，ΔE表示某些即将过期的物资由于转运至更有条件使用其的地区而增加的期望价值。易见，在一定概率下满足物资需求并同时最小化预储总成本CT+CB-ΔE就是预储调整活动的目标。

据此我们可以给出以下最优化模型来描述预储调整活动的决策问题：

minCT+CB-ΔE

s.t.

(2)

随后，我们将逐个给出运输成本、购买成本和物资期望使用价值增加量的表现形式。

运输成本CT是由于物资运输导致的成本。这里我们把CT考虑为两个部分：车辆租赁导致的成本以及车辆机动导致的成本。我们将在仓库Wj和Wj′之间的单向运输工作的集合定义为一个运输任务Tjj′。为方便起见，我们规定每辆车只能参与一个运输任务，且在参加的运输任务完成后不需要回到起点[26](这里值得注意的是，我们仅假设车辆在完成运输任务后不需要回到起点。实际上，车辆在任务中可以进行必要的空车机动)。下面我们首先计算单个运输任务Tjj′中产生的运输费用CTjj′，然后将每个任务产生的运输费用汇总，最终得到CT的表达式。

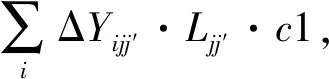
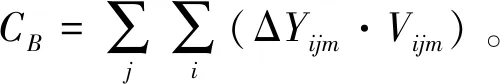
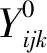
最终，我们得到如下机会规划模型(3)：

min (CT+CB-ΔE)

(3.1)

(3.2)

(3.3)

(3.4)

(3.5)

(3.6)

carcjj′≥0,j=1,…,M

(3.7)

(3.8)

(3.9)

(3.10)

(3.11)

(3.12)

(3.13)

(3.14)

我们对模型(3)的详细解释如下：

(3.1)为预储活动的总成本目标函数；

(3.2)给出了物资预储量可以满足需求的机会约束；

(3.3)给出了预储调整活动结束后各仓库各物资存量的计算方式；

(3.4)为总运输成本的计算方式；

(3.5)表示从Wj处参加运输任务Tjj′的车辆数不能多于其所运往Wj′的所有种类物资总量(以车为单位)；

(3.6)和(3.7)共同给出了从Wj处参加运输任务Tjj′的车辆为了完成任务Tjj′所需进行的两地之间空车机动次数；

(3.8)给出了物资购买成本的计算方式；

(3.9)给出了物资期望使用价值改变量的计算方式；

(3.10)和(3.11)共同给出了Wj在物资预储调整后所拥有的将要过期的物资Yi的期望使用价值的上限；

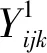
(3.13)和(3.14)共同给出了Wj的物资流出量上限。

3 基于中央级应急物资储备库的应急物资预储调整模拟

本节中，我们在假设的洪涝灾害情景下，分别采取两种策略对我国目前已建成的20座中央级应急物资储备库中所储存的物资1(Y1: 瓶装饮用水)和由1单位物资2(Y2：简易帐篷)和2单位物资3(Y3：应急被褥)组成的数量关系模块化物资M1=(1*Y2, 2*Y3) 进行模拟物资预储调整。

策略一：仅采取外部资源补充的方式对各物资储备库进行灾前应急物资预储调整；

策略二：以库库联动(内部资源再分配以及外部补充相结合)的方式对各物资储备库进行灾前应急物资预储调整。

这里值得说明的是，策略二正是我国目前所实行的灾前应急物资预储调整策略(根据《中央救灾物资储备管理办法》[1]总则第四条规定，发生(将发生)重特大自然灾害需应急追加中央救灾物资的，由民政部会同财政部制定应急购置计划)。

本案例中，各储备库物资初始存储量、在时间区间T上的物资需求分布函数采用随机生成的方式产生；两类物资的市场价格、物资的过期后残值、单位车辆租赁成本、单位距离满载成本以及单位距离空载成本由人为设定的方式产生；各储备库之间的运输距离(本案例中特指公路运输距离)为所在城市之间的实际距离。

3.1 我国的中央级应急物资储备库的基本情况介绍

目前，我国已建成使用的中央级应急物资定点储备库共有20座，分别位于北京、天津、沈阳、哈尔滨、合肥、福州、郑州、武汉、长沙、南宁、重庆、成都、昆明、拉萨、渭南、兰州、格尔木、乌鲁木齐、喀什、西安等城市(参见文献[29-30])。我国中央级应急物资储备库在不同地理区域上的分布情况如下图所示：

图1 我国中央级应急物资储备库地理区域分布图

3.2 案例数据

根据国家对于灾害响应等级的四级划分，我们随机生成了在时间区间T上20个中央库所在地区发生a(a=0,1,…,4)级响应洪涝灾害的概率Pja以及对应的物资需求，详细数据见表1及表2。

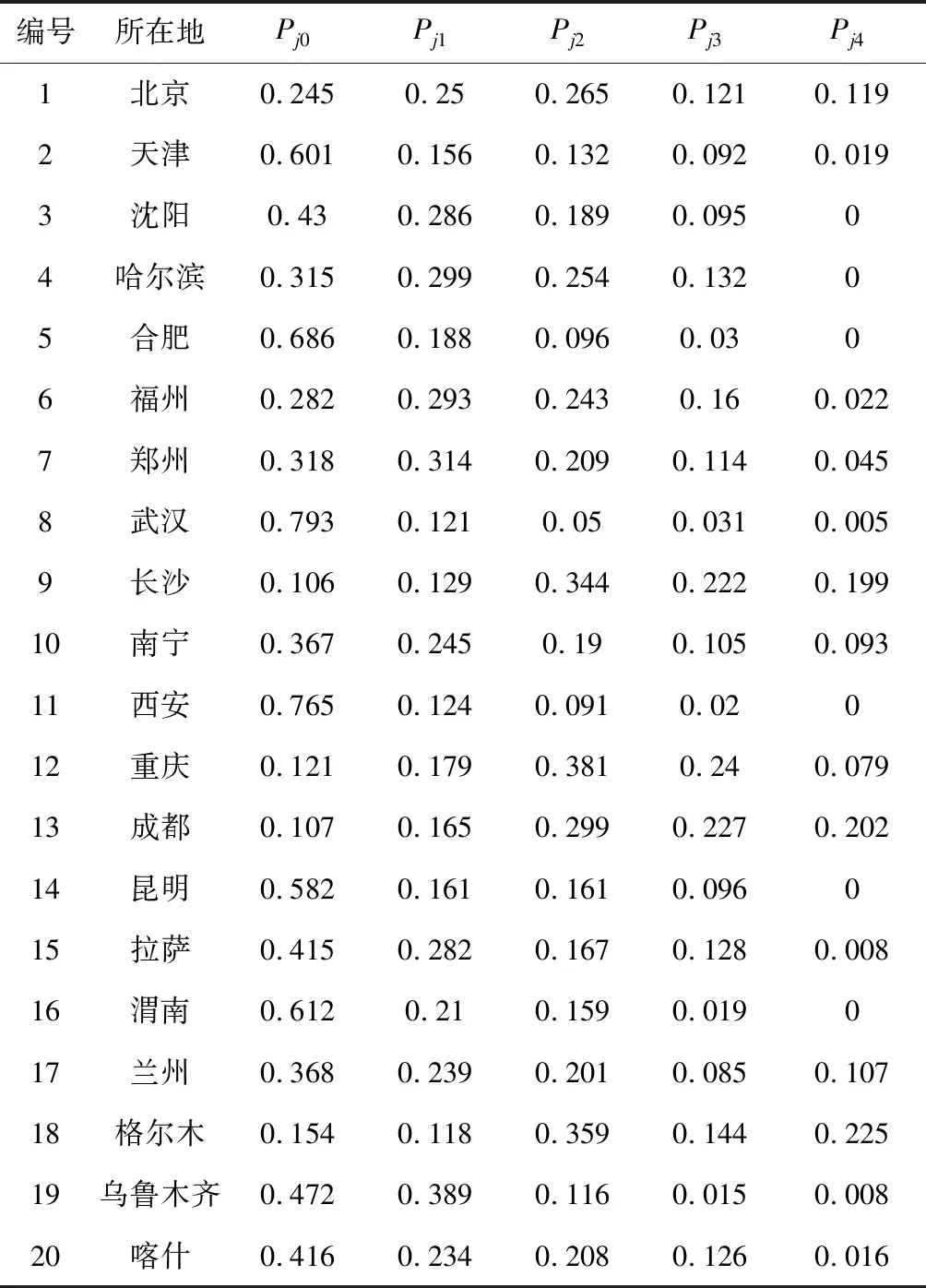
表1 各物资库发生对应级别灾害响应的概率

表2 各物资库发生对应级别灾害响应时的物资需求(单位：吨)

续表2 各物资库发生对应级别灾害响应时的物资需求(单位：吨)

我们设定了物资1与物资2在保质期内和保质期外的价值以及车辆运输成本参数，具体数值如表3及表4所示：

通过查阅电子地图，我们得到了我国20个中央级应急物资储备库之间的公路距离，具体数值如表5所示：

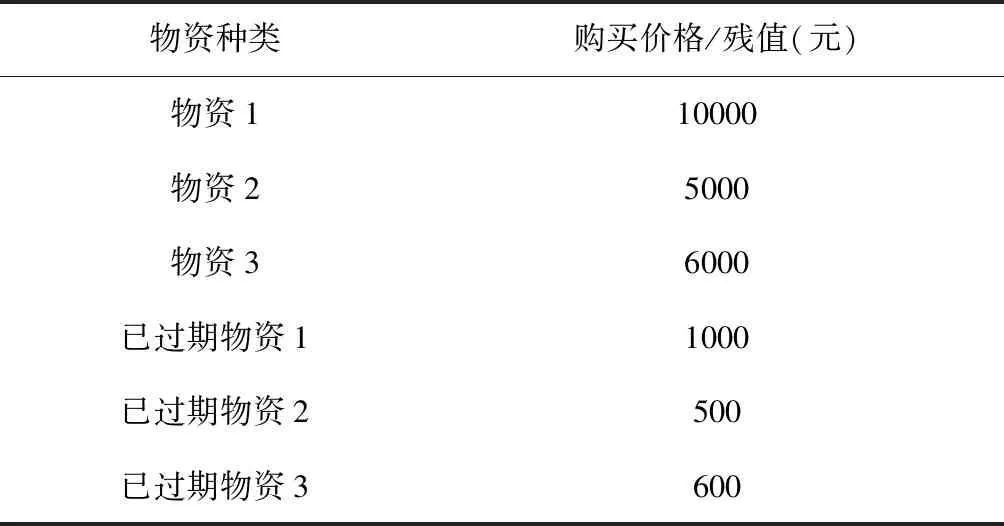
表3 物资1与物资2在保质期内和保质期外的价值

表4 车辆运输成本参数

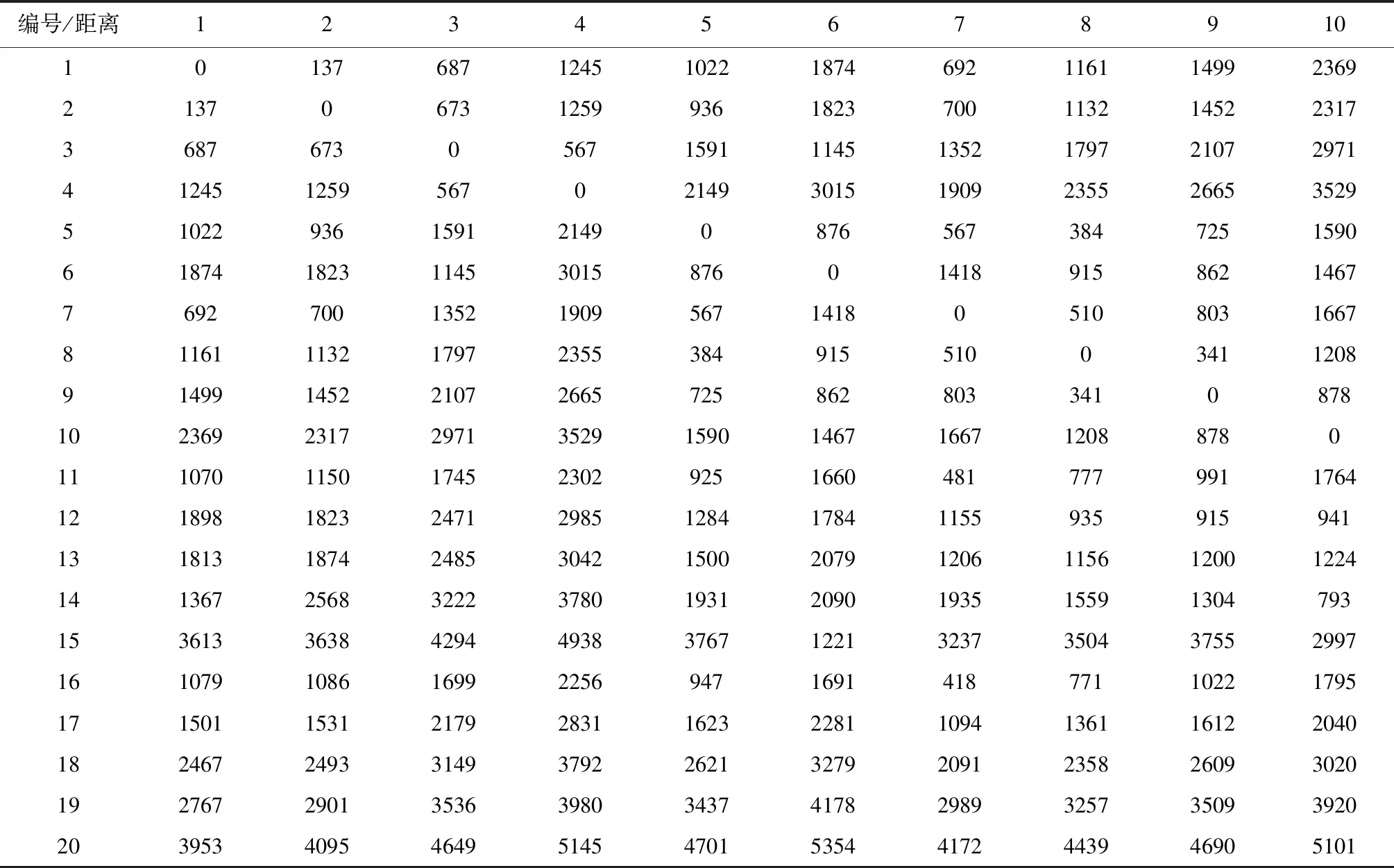
表5 城市公路运输距离表(1)

表5 城市公路运输距离表(2)

续表5 城市公路运输距离表(2)

我们通过随机生成的方法，模拟了各中央级应急物资储备库中的现有物资储存水平，具体数据如表6所示：

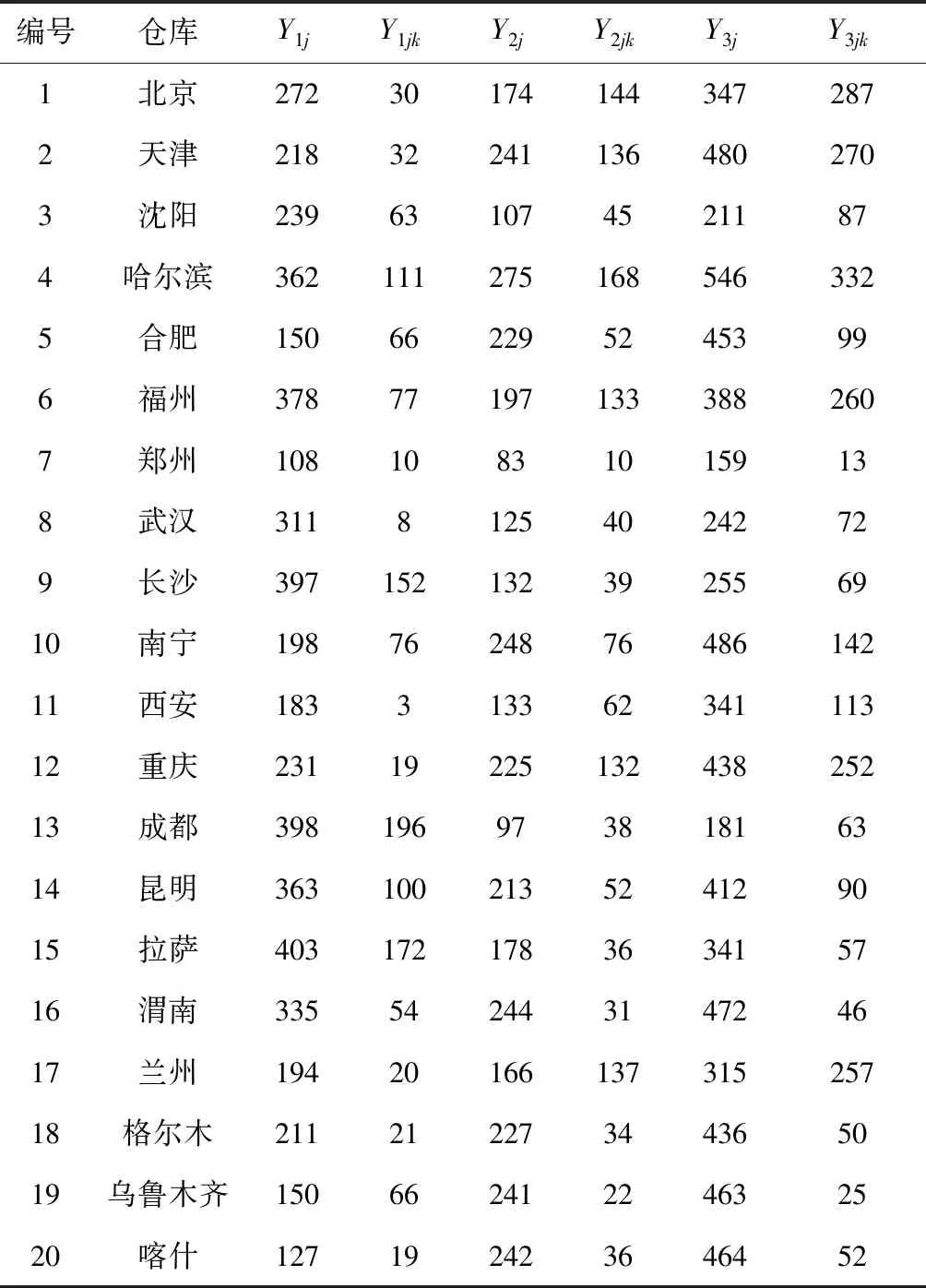
表6 各储备库物资储备初始水平

3.3 预储调整方案计算结果

3.3.1 物资预储量调整下界计算结果

在此我们假设灾前物资预储调整行动是以满足区域内各应急仓库覆盖地区90%的物资需求为约束。则通过求解最优化问题(1.1)、(1.2)以及比例关系式(1.3)，我们计算出各中央级应急物资储备库物资预储量调整下界如表7所示：

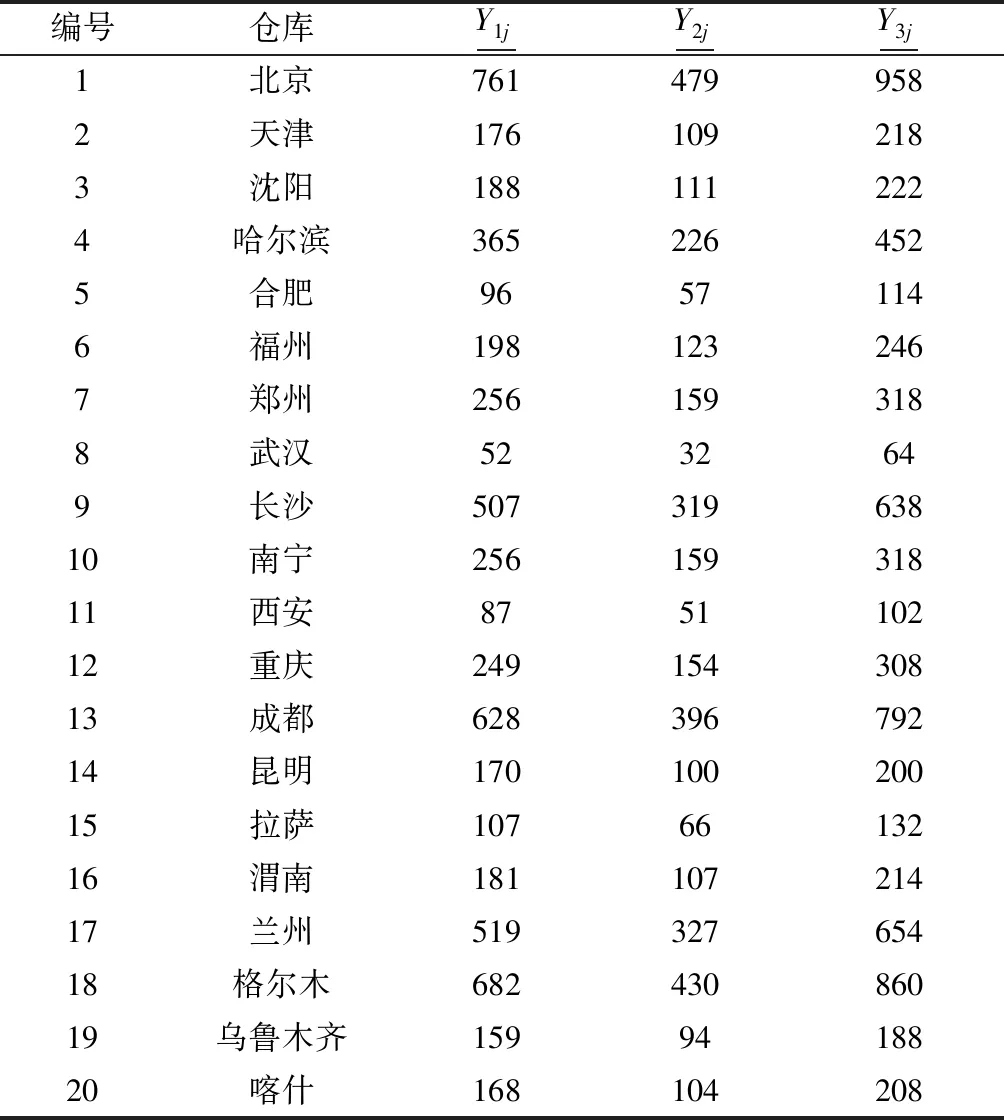
表7 各储备库物资预储量调整下界

3.3.2 物资预储调整方案计算

我们首先应用策略1对物资调整方案进行计算，该方案仅包含物资购买方案。策略1下的物资购买方案如表8所示。

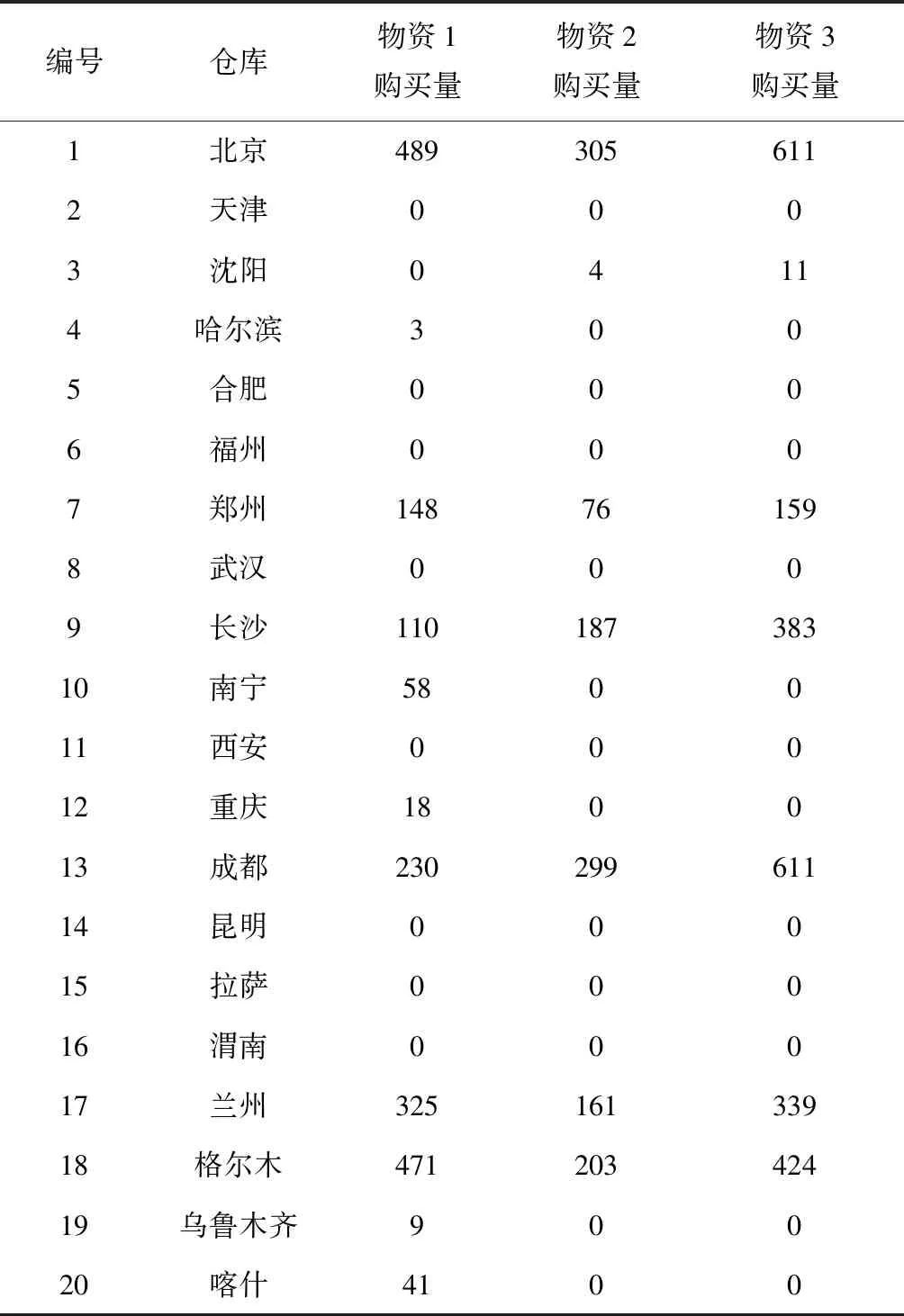
表8 策略1下各储备库物资购买方案

随后，通过使用Python编程语言对线性化后的模型(3)进行求解，我们在策略2下通过对线性化后的模型(3)进行求解并计算出物资预储调整方案。该方案由物资购买方案、物资联动方案和车辆的租赁和分配方案组成。

1)物资购买方案：

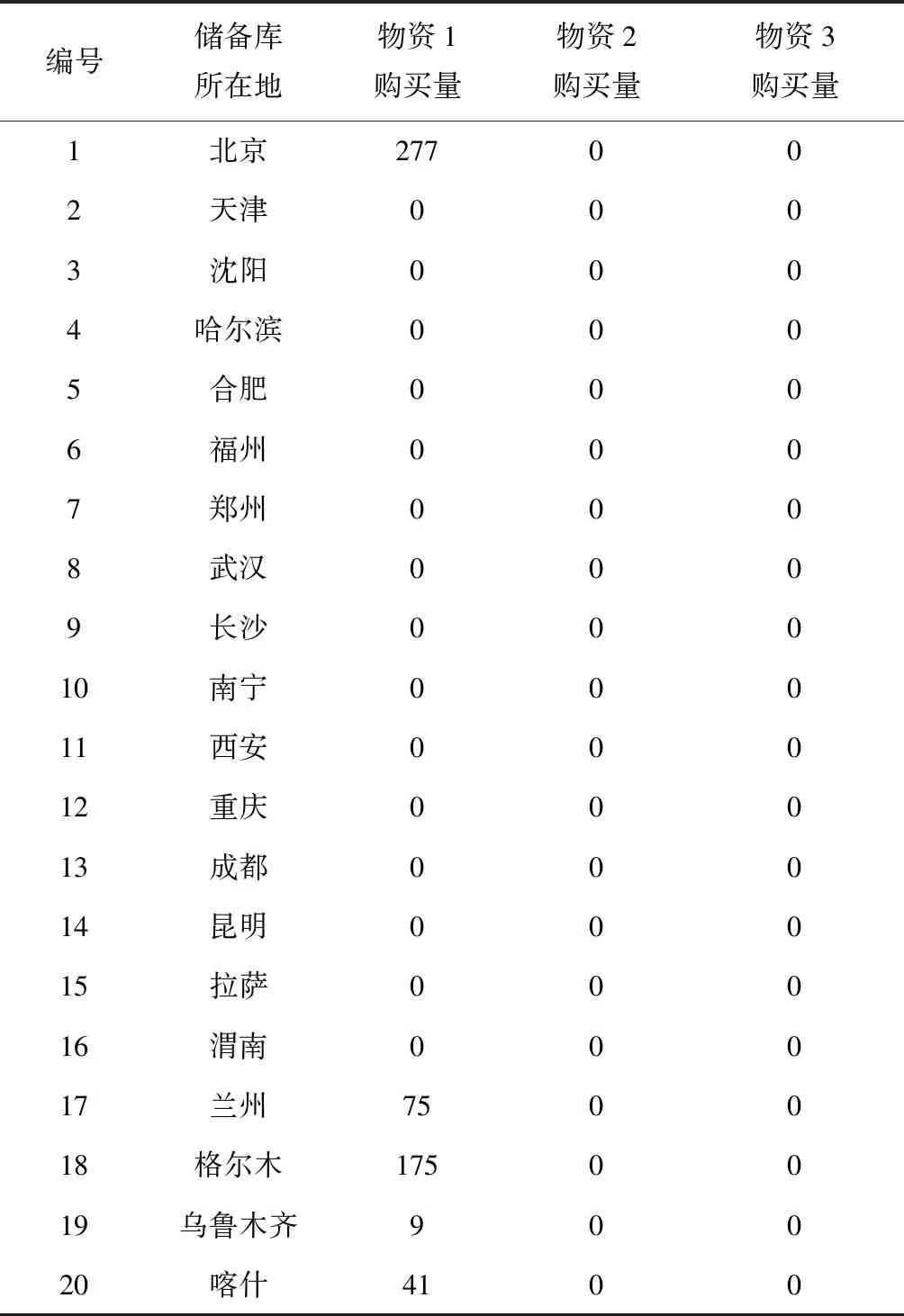
表9 策略2下各储备库物资购买方案

2)物资一调运方案(表格中的数据 ΔY1jj′: ΔY1jj′k表示从表格横坐标对应储备库调运到表格竖坐标对应储备库的物资一总量和即将过期的物资一数量)：

表10 物资一调运方案(未在此表中列出储备库即不参与物资一调运及接收)

续表10 物资一调运方案(未在此表中列出储备库即不参与物资一调运及接收)

3)物资二调运方案：

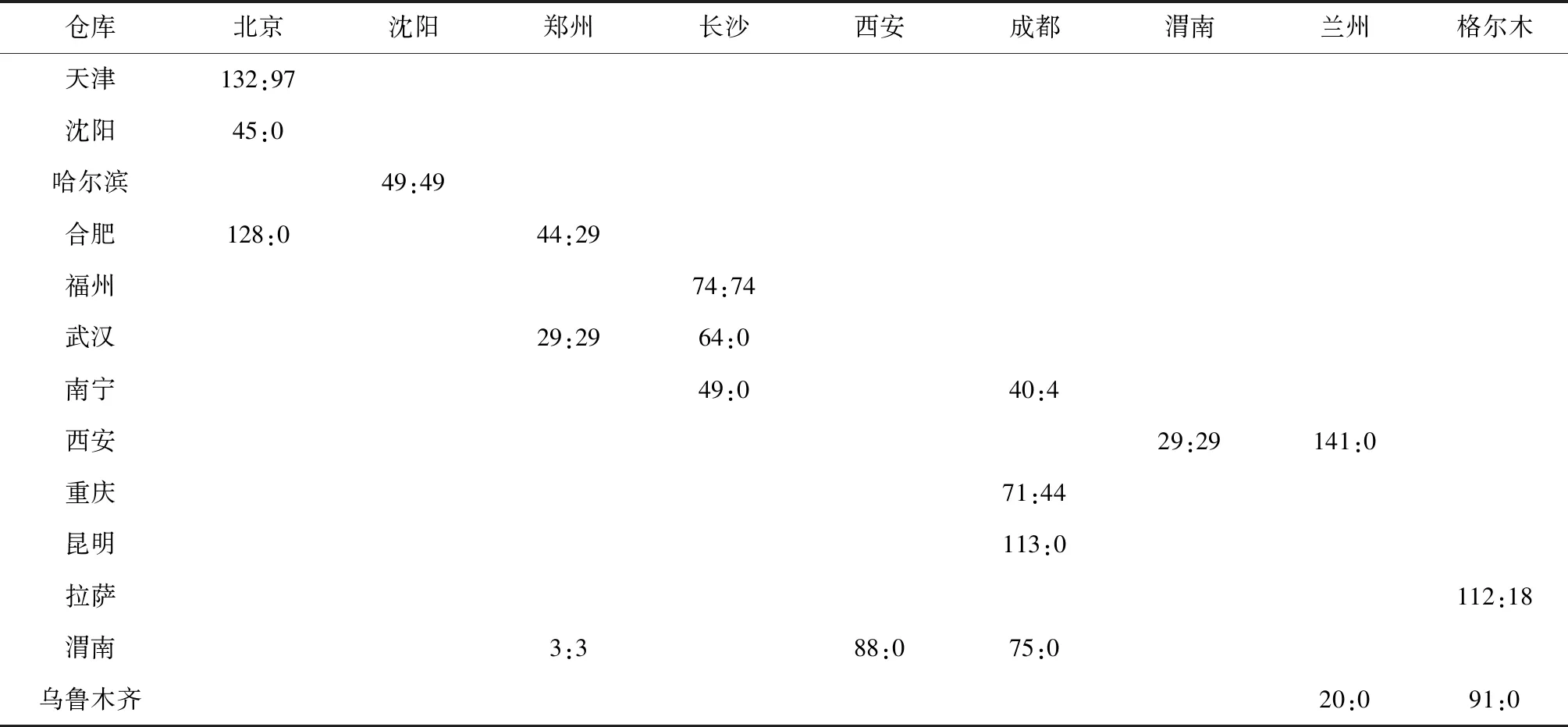
表11 物资二调运方案(未在此表中列出储备库即不参与物资二调运及接收)

4)物资三调运方案：

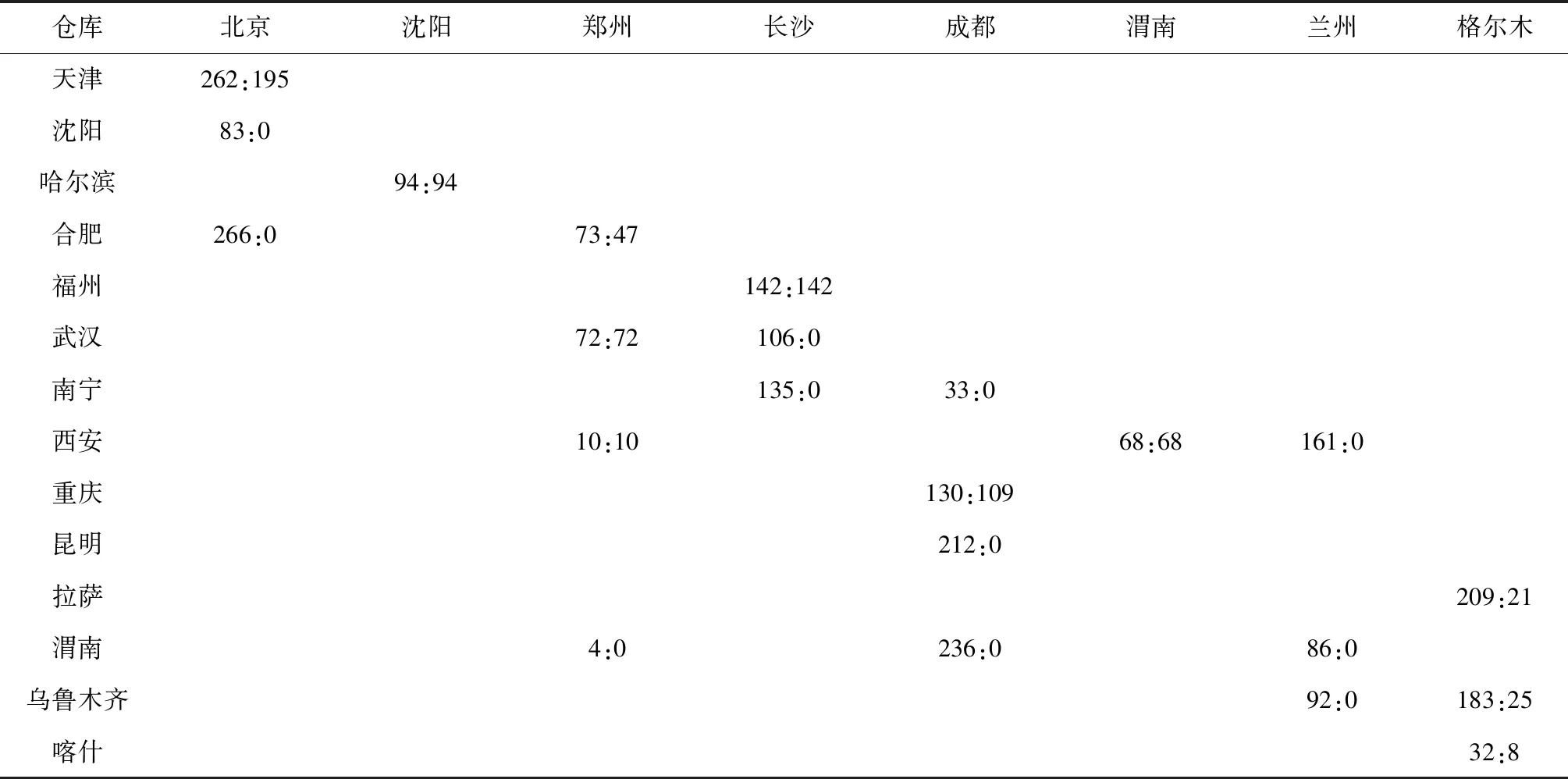
表12 物资三调运方案(未在此表中列出储备库即不参与物资三调运及接收)

5)车辆租赁和分配方案(表格中的数据表示从表格横坐标对应储备库出发到表格竖坐标对应储备库执行物资调运任务的车辆数)：

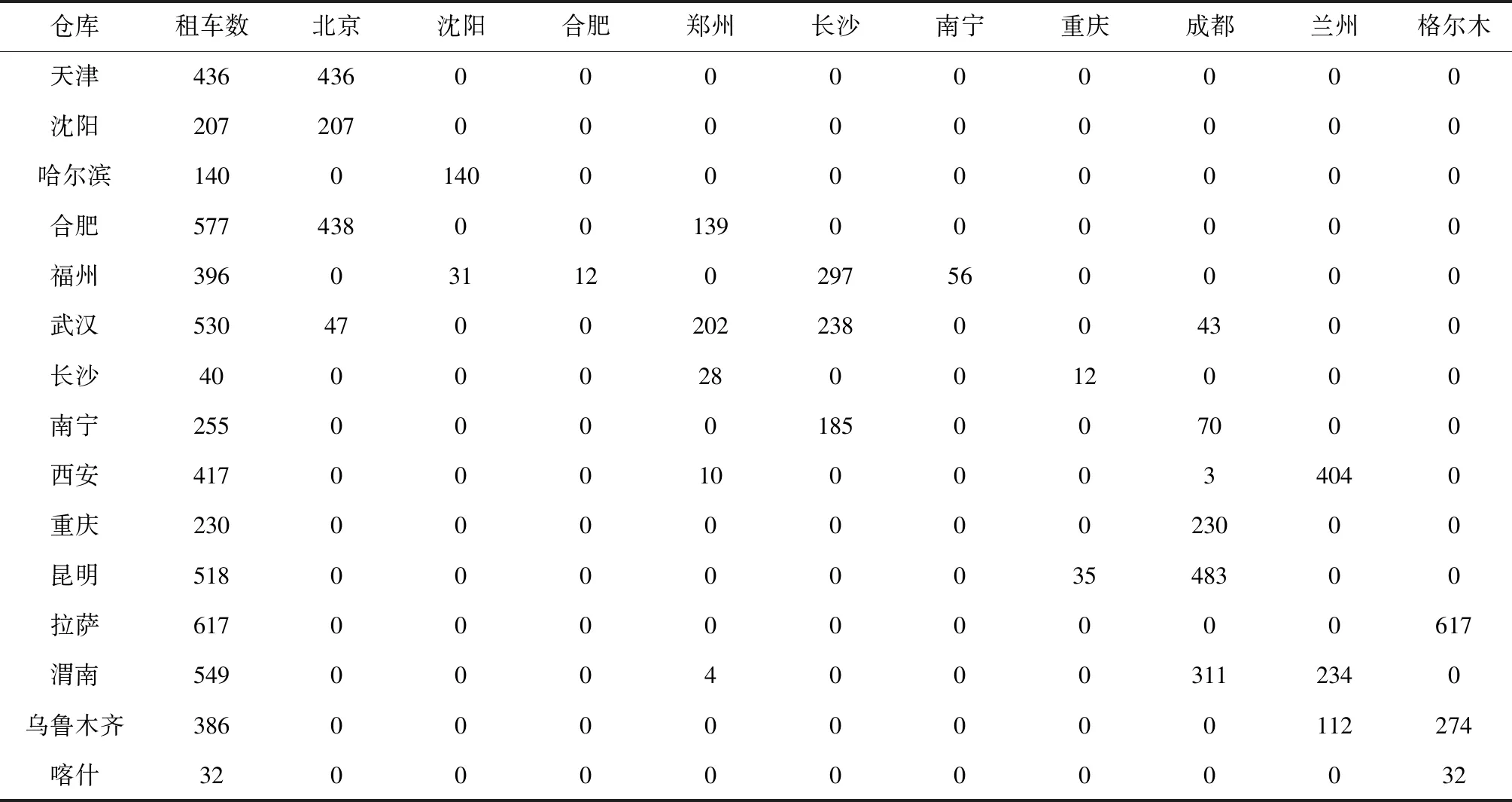
表13 车辆租赁和分配方案(未在此表中列出的储备库即不参与物资调运及接收)

6)最终，物资预储调整的总成本及其组成部分的数值如下表所示：

表14 预储调整总成本及其组成部分

3.3.3 调整方案结果分析

本案例中，我们分别采取两种策略，分别在满足各储备库在90%概率可能下的物资需求条件下，对物资预储水平方案进行了计算。如表14所示，采取策略2(库库联动策略)时，物资预储调整成本与采取策略1(不进行库库联动)时的预储调整方案成本相比降低了27680550元(约68.48%)，其中物资购买成本减少34653000元(约85.73%)，运输成本增加9336082元，物资使用价值增加2363632元。值得注意的是，本案例中大部分数据为模拟数据，所以在实际数据条件下，采取两种策略的物资预储调整成本差距可能没有本方案中如此明显。然而，由于策略1的可能行动集合中包含策略2中的所有可能行动(库库联动机制允许仅以市场购买方式调整物资储备)，所以在策略1下进行的最优化物资预储水平调整方案成本必定会小于或等于在策略2下的最优化预储调整方案成本。此外，当条件适合时(如仓库间运输距离较短、物资需求期望差距较大时)，采用库库联动机制将会在很大程度上减少物资预储水平调整成本。

4 结语

本文基于物资模块化和物资需求分布已知的假设，在考虑物资时效性的情况下建立了以满足一定物资保障度下的应急预储要求为约束，以预储调整总成本最小为目标函数的灾前物资预储水平调整与轮转机制(库库联动机制)。该机制以储备库之间的物资调运和市场购买为调整手段，可以在一定概率下满足各物资储备库在未来一段时期内的物资需求。最后，本文将库库联动机制应用到我国20个中央级应急物资储备库的应急物资预储调整模拟中，得出了较为经济有效的库库联动方案，与不采用库库联动方法相比降低了68.48%的物资预储调整成本，从而也验证了库库联动模型的经济性和实用性。

目前，本文提出的库库联动机制仅考虑了公路运输一种物资调运方式，然而在实际中可能会有铁路运输、航空运输等多种运输方式。此外，本文目前仅在各物资储备库在未来一个时间段上(单期)的物资需求分布预测信息下进行库库联动。在未来的研究中，在综合考虑多式联运和多期的物资需求分布预测信息的情况下进行库库联动将会是新的挑战和方向。