基于特征点的非刚性图像配准算法

谷皓 程远志

摘 要：针对非刚性点配准问题，主要是解决寻找对应关系的问题和求解空间弯曲变换。而对于数据退化严重，离群点和噪声增多的情况，现阶段还未见到有效的技术设计方案。这需要研究能在关注图像全局特征的同时也能关注图像的局部特征。在本文中，将配准问题视为概率问题，用高斯混合模型（GMM）来描述输入的特征点集。通过将寻找点对应关系问题转化为估计混合密度的问题，使得一个特征点集的高斯密度质心与另一个特征点集保持一致。并且利用局部特征和确定性退火的方法来保证本文的方法在遇到离群点和噪声的情况下也能正确地完成任务。对于求解空间变换，通过使用薄板样条平面的非刚性空间映射来对要求解的空间变换进行参数化。研究通过使用一些通用的数据集合和一些实际的数据集合来证明本文方法的普适性和鲁棒性，并且和目前已经发表的流行方法进行对比。

关键词： 非刚性配准;高斯混合模型;空间变换

文章编号： 2095-2163（2019）03-0079-07 中图分类号： TP391.41 文献标志码： A

0 引 言

目前，基于特征的配准问题是一个热门的研究方向。该技术在计算机视觉、机器学习、医学图像处理、模式识别以及地理信息系统中发挥着至关重要的作用。简单来说，配准问题就是找寻2幅图像之间的最佳空间变换和匹配。最简单、基础的特征表示方式就是运用点特征。但是，只用点特征来解决基于特征的图像配准却颇具现实难度。

时下，国内外已经陆续涌现了很多基于特征点的图像配准方法。迭代最近点（ICP）算法[1]是最早的、也是最著名的点集配准算法之一。算法中，假设最近的点为对应点，通过最小化均方距离来得到转换矩阵，但是ICP却仅是适用于刚性配准的研究。TPS-RPM算法[2]采用薄板样条作为非刚性映射，使用软分配和确定性退火来解决联合优化的问题。形状上下文（Shape Context， SC）[3]描述符是基于物体轮廓样本点进行描述的，将所有点的形状上下文组合起来就可以形成整个物体的形状上下文了，接下来就是对已有的形状进行匹配的算法运行过程。文献[4]首先使用特征描述子建立点的对应关系，然后使用再生核Hilbert空间（RKHS）来求解变换函数，还可通过添加鲁棒的L2E估计子来处理噪声和离群点。GMMREG算法[5]是较早的使用高斯混合模型（Gaussian Mixture Model， GMM）来表示2个点集的方法，其中通过最小化2个高斯混合模型的L2距离来求解配准问题。而当下学界使用高斯混合模型来描述点集数据也已成为研究趋势。文献[6]采取了一种非对称的高斯混合模型来寻找点集之间的对应关系。Myronenko等人[7]发表了著名的一致性点漂移（Coherent Point Drift， CPD）算法，就是将配准问题视为概率密度估计问题，最大化模板点集高斯混合模型的中心和目标点集的最大似然函数，通过快速高斯变换和矩阵低秩逼近来提高配准的速度，但是对噪声和离群点的鲁棒性仍未臻优良。国内的秦红星等人[8]提出以信息论为理论基础，相对熵度量点云相似度的KL-Reg算法。该算法不需要显式地建立对应关系，首先将点云数据建模为高斯混合模型，然后用相对熵度量高斯混合模型间的分布距离，最后选用最小化分布距离计算模型变换。王安娜等人[9]提出一种基于特征点匹配的非刚性配准方法，通过双向匹配对应点建立匹配关系，采用粒子群优化算法寻找最优变换参数。

综上论述可知，在本文中，研究提出了一种新的非刚性配准算法。算法中利用高斯混合模型来表示研究的点集，利用估计概率密度的方法来构建目标函数，利用局部特征和确定性退火的方法来保证本文的方法对噪声和离群点的鲁棒性。使得配准精度得到提高，并在大部分实验中超越其余算法。

相对于公式（5），研究增加了一个新的正则化项，这一项其实就是Q（zm=n; θold）与πmn的KL距离，也就是说研究不希望当前求得的p（zm=n）与预设的先验概率差距过大，而這个由前文的新系数T来控制，当T较小时，公式（6）和公式（5）没有区别，主要关注的是全局的变换;当T较大时，限制更多，主要考虑的是局部的变换。研究还将引入确定性退火的方法，从较大的T开始，逐渐减小T的值，最终达到收敛。

1.2 给先验概率赋值

在1.1节研究引入了一个先验概率πmn来表示目标点ym与变换后的模板点f（xn）配对的先验概率。对于这个先验概率，一般是采用使得每个目标点到每个模板点概率相同的方法，即πmn=[SX（]1[]π[SX）]，而这里需先使用局部特征的方法来展开一轮粗略的配准用来给研究的πmn进行赋值。具体方法是使用形状上下文（SC）描述符来进行一轮粗略的配准，得到一个目标点集和模板点集的初始对应关系，再利用这个对应关系来给πmn提供赋值。

文中使用Im来表示与目标点ym存在对应关系的模板点的集合，Im={xa1， xa2，…，xak; 1≤xau≤N， 1≤u≤k}，其中k为集合的个数。

如果k=0，也就是说没有模板点与研究中的ym相匹配，故而采用πmn=[SX（]1[]N[SX）]， n∈NN的方法来实现对文中先验概率的赋值。

如果k≠0，也就是说存在模板点与研究中的ym相匹配，故而采用下面的公式来给先验概率赋值：

综上所述，该过程就是利用了数据集的局部特征来给文中的先验概率赋值，再结合此处的超参T和KL距离的正则化项，可以在T较大的时候，更多地考虑研究涉及的局部特征。

1.3 EM算法求解

设计中采用了GMM的模型来建立文中的目标函数，基于此可通过使用EM算法来研究解决这个问题。对此可阐释解析如下。

（1）E-步骤：对于现有的参数θold，运算求出Q（zm=m; θold）的值，可参考计算公式如下：

（2）M-步骤：接下来，需要更新本次研究的参数，数学公式可表述如下：

1.4 变换函数的求解

对于应用中的函数f： RDRD，在本文使用薄板样条的方法来建立研究的空间变换函数，给出其映射关系为：

其中，矩阵d是一个（D+1）×（D+1）的矩阵，表示仿射变换;矩阵w是一个k×（D+1）弯曲系数矩阵，表示非仿射变换。向量（xn）是生成的TPS核，对于每个点xn都能产生一个1×K的向量，产生式为：

为此，需要选择K个控制点。

研究中，将公式（6）去掉与f不相关的部分，可以得到关于TPS的能量函数为：

其中，正规化参数λ用于调节非刚性形变系数w，正则化参数μ用于调节刚性仿射变换系数d。而这2个参数也都会加入研究的退火过程中（λ=λ0T， μ=μ0T），如此将利于求出全局最优解。而Qp是Q（zm=n; θold）构成的矩阵。

为了计算d和w，还需对矩阵X进行QR分解，分解成仿射和非仿射弯曲空间。变换公式见如下：

2 算法框架

算法1 新的非刚性配准算法

输入 2个点集X和Y

输出 变换函数f

初始化参数T，λ和μ。

初始化参数c，η，w和d。

repeat

repeat

E-步骤：

利用特征描述子计算Y和f（X）的初始对应关系;

利用公式（7）更新πmn;

利用公式（8）更新Qp;

M-步骤：

利用公式（9）更新η;

利用公式（14）和（15）更新w和d;

until θ收敛

减小T，λ和μ。

until T=Tfinal

3 实验结果

为了估测本文算法的性能，这里拟将进行3个方面的实验研究，分别是：

（1）二维非刚性配准。

（2）三维非刚性配准。

（3）图像特征点配准。

文中使用Matlab实现设计算法的主要过程，并且与GMMREG算法和rpm-tps算法进行比较。研究内容详见如下。

3.1 二维非刚性配准的结果与分析

研究采用文献[2]中的公共数据集，这是金鱼形状的点集。其中，‘+表示目标点集，‘o表示模板点集，总共为98个点。该设计旨在考察本文算法在有缺失点的情况下的配准情况。

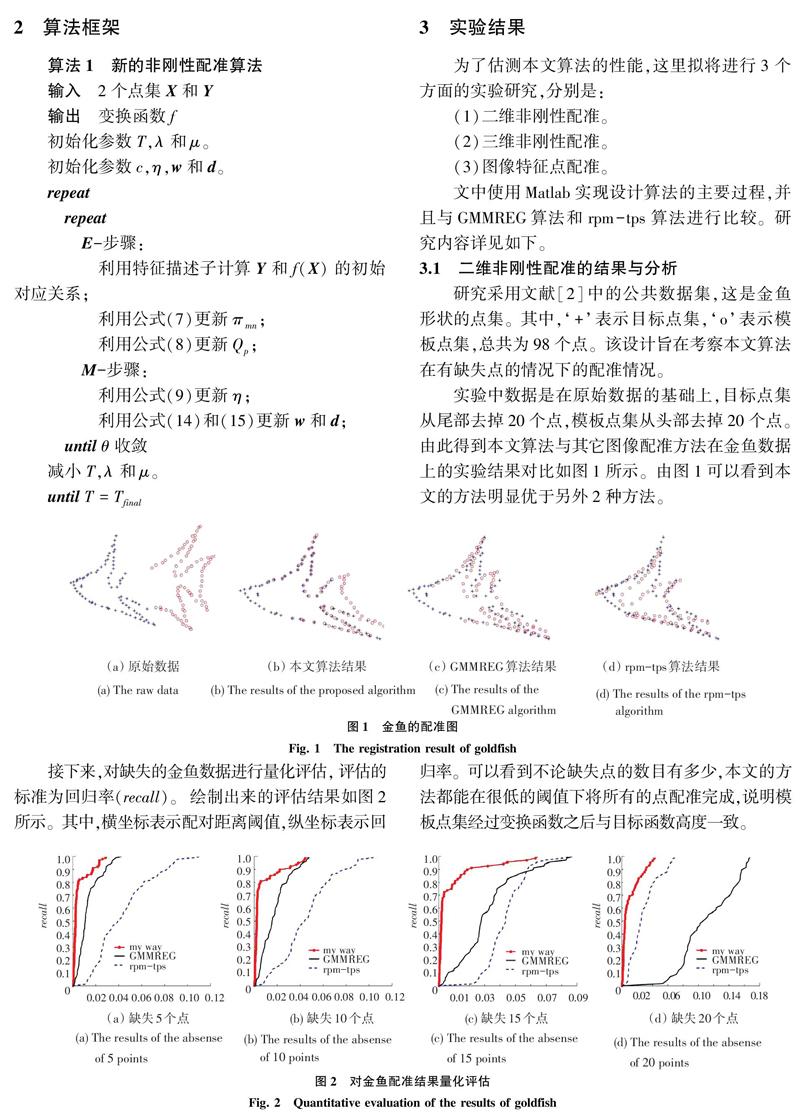
实验中数据是在原始数据的基础上，目标点集从尾部去掉20个点，模板点集从头部去掉20个点。由此得到本文算法与其它图像配准方法在金鱼数据上的实验结果对比如图1所示。由图1可以看到本文的方法明显优于另外2种方法。

接下来，对缺失的金鱼数据进行量化评估，评估的标准为回归率（recall）。绘制出来的评估结果如图2所示。其中，横坐标表示配对距离阈值，纵坐标表示回归率。可以看到不论缺失点的数目有多少，本文的方法都能在很低的阈值下将所有的点配准完成，说明模板点集经过变换函数之后与目标函数高度一致。

3.2 三维非刚性配准的结果与分析

研究中采用了文献[5]中的公共数据集来进行实验，这是人脸形状的点集，‘+表示目标点集，‘o表示模板点集，总共有392个点。该设计旨在考察本文算法在有噪声和离群点的情况下的配准情况。对此方面研究可探讨论述如下。

（1）加入高斯白噪声。如图3所示，是在原始数据的基础上人为加入高斯白噪声（均值为0、方差为noise），而图3的第一列到第四列的noise值分别为：0.03，0.06，0.09，0.12。观察发现，在低噪声的情况下，3种方法得到的结果都不错，对配准结果影响不大，但是在高噪声的情况下，可以看到3种算法均受到了一定影响，但是本文的算法效果卻更好。此处针对量化结果拟展开具体分析如下。

对于在不同噪声条件的情况下，3种算法的误差的平均值和方差的运算结果对比则如图4所示，这里的误差是用变形之后的模板点集与目标点集对应点的欧氏距离。可以看到，本文的方法不论是在误差的平均值、还是方差上都比其它的方法要更好，并且随着噪声的增加，误差也没有发生明显变化。

（2）加入随机离群点。加入不同数目的随机离群点后，本文算法与GMMREG算法、rpm-tps算法的实验结果对比如图5所示。其中，图5的第一列到第五列分别加入离群点数目为：40、80、120、160、200。可以看到本文的方法对于加入离群点之后依然做到了优等级别的配准，且均超过了其它2个算法的实验结果。此处针对量化结果拟展开具体分析如下。

对于在不同数量离群点的情况下，各类算法误差的平均值和方差结果如图6所示，这里的误差是用变形之后的模板点集与目标点集对应点的欧氏距离。观察后得知，本文的方法不论是在误差的平均值、还是方差都比其它的方法要小，并且随着噪声的增加，误差几乎没有较大变化，很稳定。

3.3 图像特征点配准结果

前文论述的都是对于点集的实验结果，下面将给出本文的算法在现实图像上的实验结果。此处的数据来自于牛津走廊序列（Oxford corridor sequence）数据集，这个数据集是对于同一个走廊连续拍摄的一系列照片，图像都是512×512像素，研究从中随机选取了2张。

图7是在原图的基础上利用harris角点检测方法，提取出特征点后，再用本文的算法来对提取的特征点进行配准。

图8就是对图7中2张照片中提取的角点应用3种算法的配准结果，其中‘+表示目标点集，‘o表示模板点集。可以看到，对于真实的图片数据，本文的算法也能得到良好的配准结果，而且均要胜过其它2种方法的实验结果。

4 结束语

本文提出了一个新的非刚性配准算法，通过使用高斯混合模型（GMM）来描述输入的特征点集，将寻找点对应关系问题转化为估计混合密度的问题，使用薄板样条平面（TPS）来描述空间变换函数。并且利用局部特征和确定性退火的方法来保证本文的方法在遇到离群点和噪声的情况下也能正确地达到设计目标。最终的测试实验证明本文提出的方法能有效避免离群点和噪声这种数据退化对图像配准所带来的干扰，相较其它的配准算法，能取得更好的配准精度和效果。下一步的研究工作是提高该算法的效率，使得能在更短的时间完成图像配准任务，并实现更大范围的应用推广。

参考文献

[1]BESL P J， MCKAY N D. A method for registration of 3-D shapes[J].  IEEE Transactions on Pattern Analysis and Machine Intelligence， 1992，14： 239-256.

[2] CHUI H， RANGARAJAN A. A new point matching algorithm for non-rigid registration[J]. Computer Vision and Image Understanding， 2003， 89（2-3）： 114-141.

[3] BELONGIE S， MALIK J，  PUZICHA J. Shape matching and object recognition using shape contexts[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2002， 24（4）： 509-522.

[4] MA Jiayi， ZHAO Ji， TIAN Jinwen， et al. Robust estimation of nonrigid transformation for point set registration[C]// IEEE Conference on Computer Vision and Pattern Recognition （CVPR）. Portland：IEEE， 2013： 2147-2154.

[5] JIAN Bing， VEMURI B C. Robust point set registration using gaussian mixture models[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2011， 33（8）： 1633-1645.

[6] TAO Wenbing ，SUN Kun. Asymmetrical gauss mixture models for point sets matching[C]. IEEE International Conference on Computer Vision and Pattern Recognition （CVPR）.Columbus， Ohio， USA：IEEE， 2014： 1598-1605.

[7] MYRONENKO A，SONG Xubo. Point set registration： Coherent point drift[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2010， 32（12）： 2262-2275.

[8] 秦紅星， 徐雷. 基于信息论的KL-Reg点云配准算法[J]. 电子与信息学报，  2015， 37（6）： 1520-1524.

[9] 王安娜， 吕丹， 王哲，等. 基于SIFT特征提取的非刚性医学图像配准算法研究[J]. 生物医学工程学杂志， 2010， 27（4）：763-768，784.