山西台网新国家标准震级标度与传统震级标度测定地方性震级的对比分析
2019-07-01张玲
张 玲
(1.山西省地震局,山西 太原 030021;2.太原大陆裂谷动力学国家野外科学观测研究站,山西 太原 030025)
0 引言
震级是表示地震本身大小的一个物理量,是地震的基本参数之一,地震学的研究就是从地震定位和震级测定开始的。因此,规范地震震级的测定,对地震监测预报、震害预防、应急救援等防震减灾工作和地震科学研究具有重要意义[1]。
基于国家标准《GB—17740—1999地震震级的规定》[2],中国地震局颁布了《地震及前兆数字观测技术规范(地震观测)》[3],要求我国地震台网在日常地震监测工作中测定地方性震级ML。由于测定均基于仿真后的模拟地震记录,故被称为传统震级标度[4]。由国家质量监督检验检疫总局、国家标准化管理委员会于2017年5月12日发布的新标准《GB 17740—2017地震震级的规定》(即“新震级国家标准”)[5]中,对测定地方性震级ML及使用作出了规定,文章称其为新国家标准震级标度。规定测定地方性震级ML时,继续使用以前的方法,使用5大分区量规函数,使得全国不同区域地震台网测定的近震震级更加准确。山西及邻区适用华北地区量规函数。
文章使用了匹配新震级标准的JOPEN-MSDP6.0重新测定了山西省区域地震台网2018年宽频带地震台站记录的山西及邻区ML≥2.0的地震,速度模型为“山西2015速度模型”[6-7],将结果与使用原全国统一量规函数测定结果进行对比,就地震事件震级偏差、单台震级偏差和标准偏差三方面进行分析。
1 资料选取
山西数字测震台网经“十五”升级改造后,形成了一个覆盖全省的数字地震观测台网,改扩建后的山西数字测震台网共有台站32个,全部使用24位IP数据采集器。另外,“十五”期间山西省相继建成了晋城、长治、运城、太原等地方台网,这些台网的纳入使山西数字测震台网的台站达到了57个(见第9页图1)。同时,山西台网共享邻省河北、河南、陕西、内蒙古自治区等台网共15个台站的实时波形数据,积累了丰富的资料[8-9]。
实际工作中发现,对于同一地震,由于台站所处方位角的不同,测定的震级有时差别比较大,这对台网的震级测定质量[7]、地震速报定位与分析[10]造成了一定影响。为验证新量规函数对测算地方性震级的可信度和精度,此次收集整理山西地区数字地震台网记录的2018年山西及邻区ML≥2.0地震的波形数据共150个,采用新量规函数R11(Δ)和原量规函数R1(Δ)分别对以上地震的地方性震级进行重新测定,并对其单台震级偏差和标准误差进行对比分析(见第10页图2)。
2 计算方法
按照《地震及前兆数字观测技术规范(地震观测)》的要求,我国地震台网测定近震震级时要将宽频带数字地震记录仿真成DD-1短周期位移记录,利用S波(或Lg波)的最大振幅来测定。其计算公式[10]为:
ML=lgAμ+R(Δ),
(1)
式中:Aμ为地动位移,单位μm,Aμ=(AN+AE)/2,AN、AE分别为南北向和东西向S波(或Lg波)的最大振幅;R(Δ)为量规函数(见第9页表1)。里克特1935年提出地方性震级ML及量规函数,1959年李善邦[11]根据我国所使用的地震仪器特性和我国华北地区的地震波衰减规律,得到了地方性震级的计算方法和量规函数R1(Δ)和R2(Δ)。其中R1(Δ)适用于短周期地震仪,R2(Δ)适用于中长周期地震仪。我国地震台网在计算地方性震级时使用的是R1(Δ)。
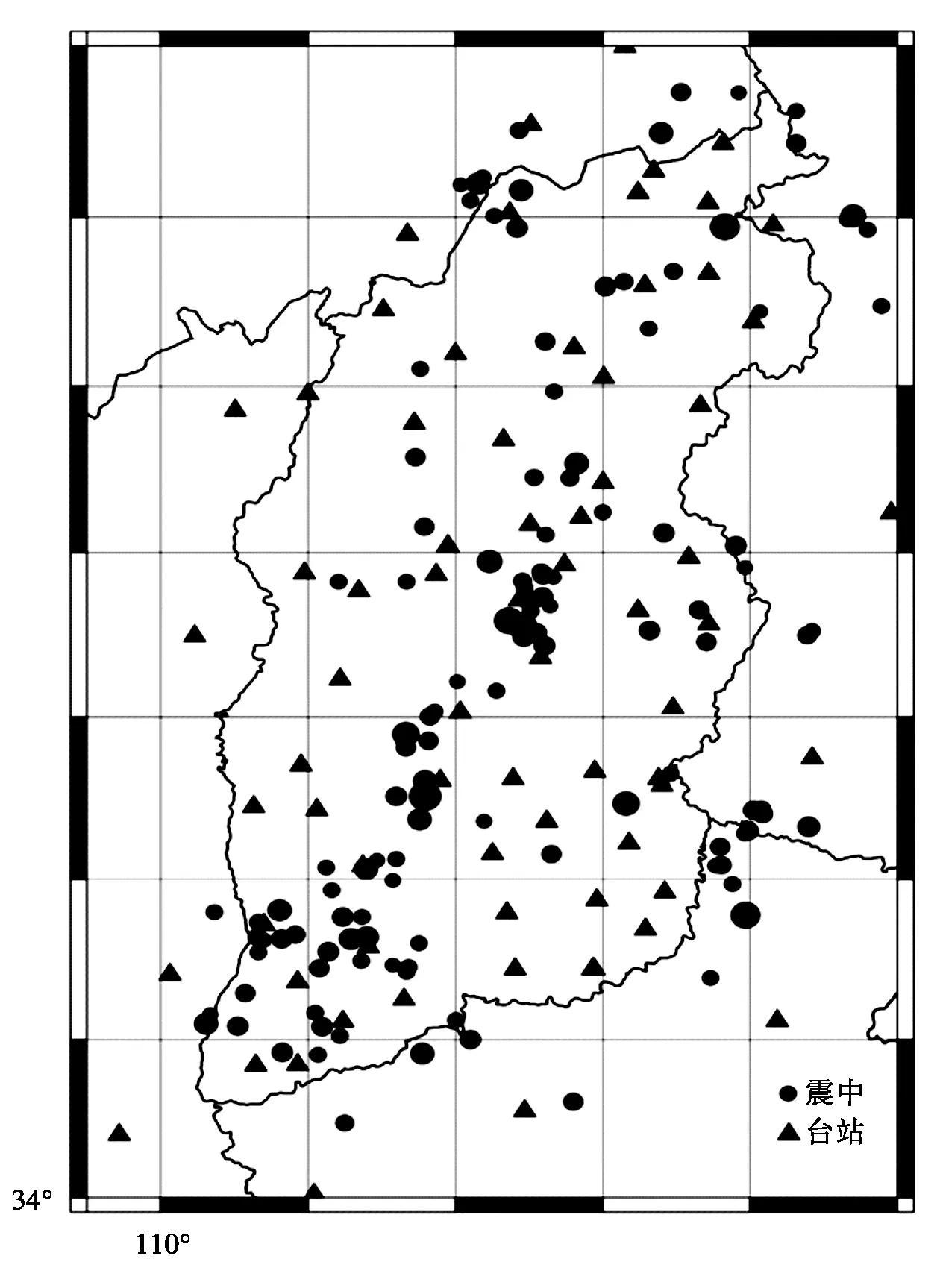
图1 山西台网ML≥2.0地震及台站分布图Fig.1 Distribution map of ML≥2.0 earthquakes and stations of Shanxi seismic network
现行的地方性震级ML的计算方法与1935年里克特的测量方法保持一致。新ML与传统ML相比,其计算公式和测定方法的差异主要是仿真模式和量规函数不同。新国家标准震级标度测定震级要求仿真成DD-1型,传统震级测定既可以仿真成DD-1型,又可以仿真成WA短周期记录,实际工作中大多数都仿真成WA型;新国家标准震级中测定地方性震级ML时使用五大分区量规函数R11(Δ),原规范的量规函数是李善邦根据我国地震仪器的特性和华北地区地震波的衰减规律得到的量规函数R1。
对于一个地震事件i,求得其第j个台站的单台震级MLij[1,12]为:
MLij=lgAμ+R(Δ)。
(2)
它的台网震级MLi即为:其对台网每个子台j测得的单台震级取平均值,即:
(3)

表1 量规函数对照表Table 1 Gauge function comparison table
对于第j个台站,它的单台震级偏差为:
ΔMLi=MLij-MLi。
(4)
它的标准偏差为:
(5)
通过以上公式,可以计算出新、旧国家标准震级下的单台偏差和标准偏差。
3 计算结果与分析
3.1 地震事件震级对比分析
对选取的150个地震事件,采用新的分区量规函数R11(Δ)和原量规函数R1(Δ)分别对ML≥2.0地震的地方性震级进行重新测定,计算得到新ML与传统ML差值如图2所示,80%的震级差值较一致,新旧震级差值绝对值都在0.1之内,二者在震级测定上变化不大。分析震级差异原因,认为新ML与原ML的不同主要体现在仿真模式和量规函数两方面。虽然新ML与原ML分别仿真成DD-1和WA两种不同模式,并测量其水平分量上同一时间的最大振幅,二者测定的振幅相同。
以2018年1月31日07时05分山西大同M3.5地震为例,选取此次地震事件记录完整的山自皂台,将其分别仿真成DD-1和WA两种短周期记录,测量其水平分量上同一时间的最大振幅。该地震的震中距为19 km,仿真成DD-1记录的振幅SMN为14.65 μm,SME为5.50 μm,测定震级为ML3.3;WA记录的振幅SMN为14.65 μm,SME为5.50 μm,测定震级为ML3.1。二者测定的振幅值相同,得出的震级相差0.2,对照表1可知,在震中距19 km处的R11与R1差值为0.2,由此可以看出,新旧震级之间的差异主要是由量规函数不同所致。

图2 重新计算得到的新ML与原ML差值图Fig.2 Magnitude difference, ΔM is the difference between the new ML and the original ML
台网震级是每个子台震级的平均值,震中距不同的台站参与震级计算时,量规函数对震级测定存在一定的影响。量规函数R11与R1在大多数震中距范围内都有差异,差值在0.1。因此次参与计算的地震事件多为小震,子台震中距基本处在0~400 km左右,在此震中距范围内R11(Δ)与R1(Δ)在Δ处于5~200 km时,R11(Δ)≥R1(Δ);Δ处于210~470 km时,R11(Δ)≤R1(Δ),从而使得台网新旧震级的差值较小,为新旧震级标度顺利过渡奠定了基础,实现新国家震级标度能够和传统震级标度很好的衔接。
3.2 单台震级偏差对比分析
图3为利用分区量规函数与原量规函数计算得出的单台震级偏差统计图,由图可知,使用新量规函数计算后得出的单台震级偏差较R1(Δ)更加集中,且向ΔMLij为0靠拢,对数据统计分析,发现利用R11(Δ)计算得到的单台震级偏差绝对值小于0.2的占到60%,0.3~0.5的占33%,0.6~0.8的占7%,大于0.9的不到1%;用R1(Δ)计算得到的单台震级偏差绝对值小于0.2的占比不到58%,0.3~0.5的占33%,0.6~0.8的占8%,大于0.9的占到1.4%。可以看出,使用新ML计算得到的单台震级偏差值93%集中在±0.5附近,且新ML比原ML占比要多。因此,认为使用新量规函数测定地方性震级ML能使单台震级偏差减小,这与王丽艳等[13]所得结论一致。
3.3 标准偏差对比
通过计算所选样本的平均标准偏差来评判测定震级的优劣程度,计算公式为:
(6)
首先用R11(Δ)通过式(4)计算所有地震事件的单台震级差,再据式(5)得出每次地震的标准偏差值δi,通过式(6)得出所有地震的平均标准误差,得出新震级国标下地方性震级标准误差δ1为0.31。同理,用R1(Δ)计算原地方性震级标准误差为δ2为0.33。δ1<δ2,

图3 新分区量规函数R11(Δ)与原量规函数R1(Δ)计算所得的单台震级偏差对比图Fig.3 Comparison diagram of magnitude deviation calculated by the new zonal gauge function R11 (Δ) and the original gauge function R1 (Δ)
表明新量规函数计算得到的震级优于原量规函数,故使用新国家标准震级标度测定地方性震级比传统震级标度测定的精度有所提高。
4 结论
运用匹配新震级标准的JOPEN-MSDP6.0重新测定了山西及邻区ML≥2.0地震震级,与原量规函数测定结果进行对比。得出如下结论:
(1) 使用新量规函数R11(Δ)较R1(Δ)计算所得的震级差值较小,震级变化在0.1之内,二者在震级测定方法上变化不大,推行新国家标准震级标度后的地方性震级ML值变化很小,可以与原地方性震级很好的衔接。
(2) 通过震级差异原因分析,虽然新震级与原震级的仿真模式和量规函数均发生了变化,并对计算单台震级产生了一定的影响,但仿真方式对地震震级的影响不大,量规函数是造成震级差值变化的主要原因,这与唐淋等[14]得出的“新旧震级之间的差异主要是仿真方式的变化不同所致”的结论不同,但得到晏绮云等[15]“江西测震台网新、旧震级国家标准测定地方性震级的对比研究”结论的支持。
(3) 使用新量规函数R11(Δ)计算所得的单台震级偏差较R1(Δ)差值更加集中,且大部分向ΔMLij为0靠拢。使用新量规函数计算所得的地方性震级标准误差较R1(Δ)值有所减小,说明在山西地区使用新国家震级标度测定ML值优于原震级标度的值,测定精度有所提高。
