基于STAR-CCM+的导管螺旋桨黏性流场计算方法研究
2019-07-01李国诚
邱 鹏,郑 高,李国诚
(武警海警学院 机电管理系,浙江宁波 315801)
0 引言
导管螺旋桨[1]是当今船舶行业主要使用的特种推进器之一,与普通螺旋桨相比,它更适用于重载、大功率的船舶中,受到国内外众多学者的关注。因此,有必要对导管桨的水动力性能进行全面地研究。目前,研究领域对导管桨的性能分析主要采用试验和数值研究的方法。试验方法的特点是方法成熟、试验结果可靠。然而近年来,随着计算机技术和流体力学理论的快速发展,数值计算方法越来越受研究人员的青睐,该方法相对于前者而言具有周期短、成本低、操作方便等优势。但是对于船舶推进器而言,绝大部分学者都是采用FLUENT流体软件进行数值研究。如朱俊飞[2]等采用FLUENT软件进行了导管桨的优化设计,赵强[3]等利用FLUENT软件对导管桨的流场进行了数值研究,李坚波[4]等采用FLUENT对导管桨间隙大小的性能的影响进行了数值研究,洪方文[5]采用FLUENT等对前置定子导管桨的流场进行了数值分析,汪蕾[6]等借助该流体软件对吊舱导管桨进行了定常与非定常数值模拟。纵观现有文献可知,采用计算流体软件FLUENT进行导管桨性能研究的方法已十分成熟。
STAR-CCM+则是一款新型CFD模拟软件,很少有学者采用此款计算流体软件进行导管桨的性能研究,该流体软件相对于FLUENT而言,其网格划分、计算、后处理的功能使用更为便利,尤其在推进器几何模型的设计优化方面更具一定的优势,且避免了 FLUENT中软件步骤重复操作的问题。因此,本文采用STAR-CCM+对导管桨进行数值模拟,与现有给定的模型试验数据进行了对比,从而证明了采用新型STAR-CCM+对导管桨的性能预报方法的有效性,为今后的导管桨黏性流场数值预报提供参考意见。
1 数值计算
1.1 三维建模
本文中计算对象[7]采用的导管为19A型,螺旋桨叶的主要参数为:直径0.2 m,毂径比为0.167,螺距比 1.0,盘面比 0.7,叶数为 4叶,叶剖面为NACA66。螺旋桨的三维型值是将已有的二维坐标转换为三维坐标,通过螺旋桨的参数和叶切面二维形状尺寸,建立与螺旋桨上曲面型值点空间坐标之间的关系式[8],最后将生成的三维型值点直接导入到Icem中形成螺旋桨的桨叶。导管可直接将二维剖面在UG软件中绕X轴旋转360°即可得到三维模型。最终导管桨的物理模型如图1所示。

图1 导管桨三维模型
1.2 控制方程
在黏性流体运动学和动力学中,RANS方程是必不可少的控制方程,本文采用CFD技术进行船舶推进器的水动力性能求解也是基于此控制方程的。RANS方程是在雷诺平均法中,将瞬时状态下的质量守恒方程和动量方程的流动变量用平均值和脉动值之和代替,并对时间取平均值,即可得到如下的RANS方程组式(1)与式(2)。


1.3 湍流模型
数值计算方法中采用了 Realizablek-ε湍流模型,此模型较好地避免了在处理标准k-ε模型均应变率特别大时,会出现正应力为负的问题,Realizablek-ε模型中湍动能k输运方程如式(3),湍流耗散率ε输运方程如式(4)。


式中:∂k=1.0;∂ε=1.2;C2=1.9;
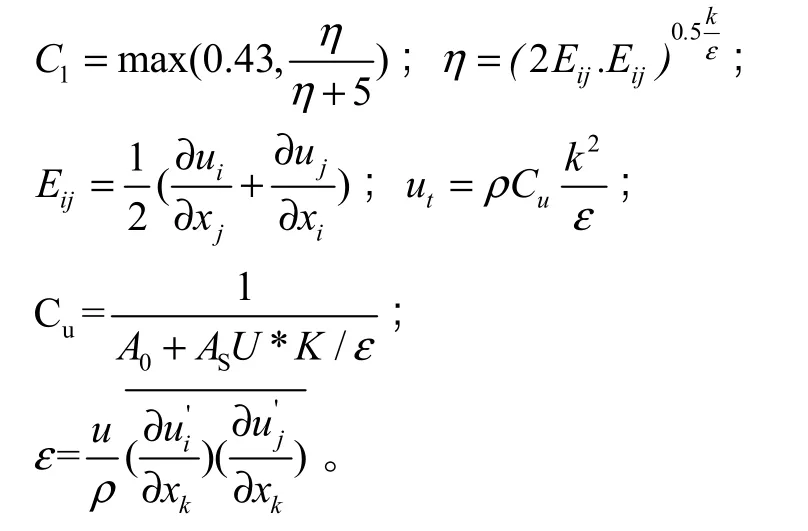
式中:


1.4 计算域及网格划分
整个计算域分为远场静止域和包含螺旋桨的旋转域,如图2所示。其中计算域的入口距离桨盘中心为8D(D为螺旋桨的桨叶直径),计算域的出口距离桨盘面中心轴向距离为10D,整体计算流域圆柱体直径为8D。本文利用STAR-CCM+软件自带的切割体网格生成方式,网格单元为正六面体,在物面边界同时设置棱柱层网格,桨叶和导管边缘处由于曲率变化较大,采用网格局部加密的形式。
1.5 边界条件设置
通过设置静止域和旋转域实现导管桨的相对旋转运动,旋转域中包含螺旋桨,采用多重参考坐标系(Moving Reference Frame,MRF)模型实现螺旋桨的旋转模拟。静止域边界采用滑移壁面。静止域与旋转域的交界面通过设定interface来实现信息的交换,同时设定静止域入口为均匀来流速度,出口为压力出口,导管和螺旋桨均设为固壁条件。压力-速度场的耦合引用SIMPLE方法。
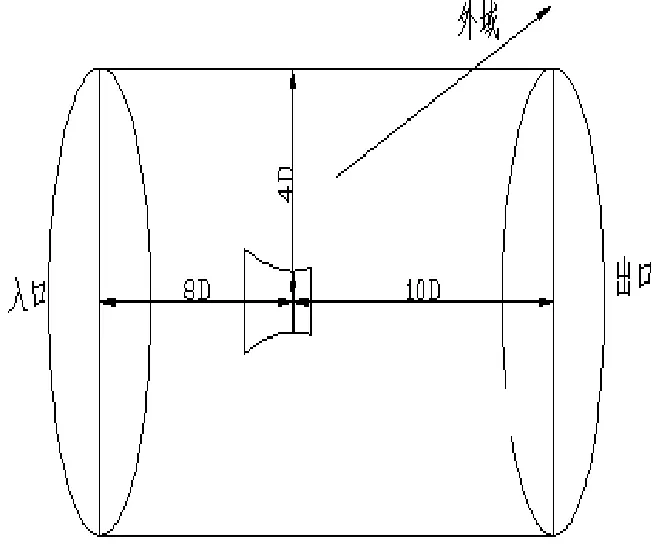
图2 计算域示意图
2 敞水性能计算与分析
2.1 网格密度的影响
为了分析不同网格密度对计算结果的影响,以进速系数J=0.3为例,对3种不同的网格密度下的模型进行计算,对结果进行比较分析。湍流模型暂选具有旋转效应的 Realizablek-ε,采用STAR-CCM+自带的trimmer grid网格划分技术对其进划分。此处固定边界层的总厚度为 0.002 m,通过改变层数来改变网格到螺旋桨表面的距离,进而影响着网格的密度(网格密度为151万、275万、428万),计算结果的误差分析如图3所示。其中误差=100×(计算值-试验值)/试验值。

图3 不同网格数目的影响
由图3计算结果可以发现,在一定的范围内,随着网格密度的增加,导管桨的推力和扭矩误差与试验值越来越接近,在网格密度为428万时,误差达到最小,总推力误差小于1.6%,总扭矩误差小于2.8%。
2.2 湍流模型的影响
为了讨论湍流模型对导管桨性能计算的影响,借助以前学者的研究结论和各种不同湍流模型的特点,本文选用STAR-CCM+自带的3种不同湍流模型,计算在同一进速系数(J=0.3)时,其对计算精度的影响。此处3种计算方案仅改变湍流模型,其余计算条件保持一致,选取上述网格数为428万的计算文件,分别采用Realizablek-ε、SSTk-ω和标准k-ε湍流模型进行数值计算,计算可得导管桨在不同湍流模型条件下的推力和扭矩大小。计算误差如图4所示。
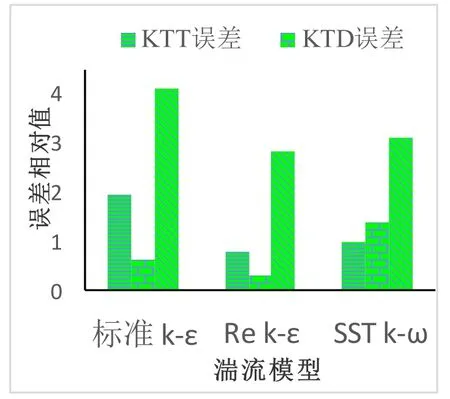
图4 不同湍流模型的影响
由图4可以看出Realizablek-ε和SSTk-ω这2种湍流模型的计算结果相差不大,均能较为准确地模拟导管桨的敞水性征。而标准k-ε湍流模型在对推力和扭矩的计算误差明显大于前2种模型的计算精度,这可能是因为对于较大流线曲率的流动而言(如螺旋桨旋转流动等),流线的曲率会发生额外的应变,湍流扩散的强度也随之加大。因此,采用该湍流模型不太适合此种模拟。故建议采用Realizablek-ε和SSTk-ω模型进行下一步研究。
2.3 敞水性征曲线分析
参考以上的计算经验,在此采用网格数量为428万,湍流模型为Realizablek-ε对导管桨的敞水性能进行数值研究,计算J从0.1~0.7的推力和扭矩系数,计算所得结果如图5所示。

图5 导管桨敞水性征曲线
由图 5导管桨敞水性征曲线能够得出如下结论。
1)在大部分工况下,本文所采用的数值计算方法所得的计算值与试验值吻合度较好,推力误差最大值不超过 5%;扭矩的计算值均高于试验值,最小误差为2%,最大误差低于6%。
2)在高进度系数时,负荷偏差增大。主要在高进速系数(如J=0.7)时,导管桨的推力、扭矩的试验值和计算值都相对较小,因此对于数值的波动都比较敏感,导致误差增大。但总体而言,本文采用STAR-CCM+进行导管桨性能计算的方法是准确可靠的。
2.4 云图分析
本节将从流场信息细节中,对导管桨的性能进行分析,主要以进速系数J=0.3为例分析数值计算结果。
由螺旋桨表面Yplus值分布(见图6)可以看出:桨叶大部分区域Yplus值主要分布在30~75之间,在导边、随边以及桨叶叶根处的Yplus值比较低,这是由模型曲面比较复杂的部分进行了网格加密导致的;本文计算选取的湍流模型Realizablek-ε通常要求 Yplus<200,计算所采用的网格划分方案得到的Yplus值满足湍流模型适应性的规定。
图7为导管桨尾流速度流线图。经过导管桨的旋转抽吸作用后,从尾流图中可以明显观察出导管桨旋转桨带动尾流旋转的特性:在桨径范围内,尾流速度流线的旋转效应很明显;在桨径范围外,随着尾流的发展,其流线的旋转效应局部减弱。这与螺旋桨旋转时对流经其表面的流体会产生强烈抽吸作用的事实相符。

图6 螺旋桨表面Yplus值分布图

图7 导管桨尾流速度流线图
从导管螺旋桨的压力云图8和图9中可得:螺旋桨的叶背压力小于叶面压力,从而形成推力向前,桨叶中间区域的曲面较光顺,因此压力分布均匀。导管的外表面及桨后方压力均大于对应的内表面和后部压力,在此工况下,导管形成正推力。压力云图显示结果与数值计算结果、基本事实相符。

8 导管及叶背压力云图

图9 导管及叶面压力云图
3 结论
本文采用计算流体软件STAR-CCM+,计算了不同工况下导管桨的敞水性能,分析了流场特点,并讨论了网格密度和湍流模型对数值计算精度的影响。结果表明:1)在一定范围内,网格越密,导管桨的计算精度越高;2)Realizablek-ε和SSTk-ω模型更适合模拟导管桨的水动力性能,所得到的计算结果与试验数据能很好地吻合;3)流场的云图分析与导管桨旋转作用时的流动事实基本基本吻合,验证了采用新型流体软件STAR-CCM+进行导管桨黏性流场数值预报的可靠性。
