广义积分的几种计算方法解析

韩丽芳

(山西大同大学浑源师范分校，山西 浑源 037400)

广义积分在实际问题中应用涉及面非常广泛，其概念相对抽象，是高等数学学习中一个知识难点。广义积分计算与定积分计算完全不同，因其形式多种多样，因此，计算方法比较灵活，较难掌握。如果单纯根据定积分定义计算，通常会发现不同程度的困难，甚至求解不出，达不到解题要求。因此，为了有效计算广义积分，本文根据数学分析中二重积分、拉式变换等相关理论，给出几种常见情形的广义积分求法，以供学习者参考。对于特殊领域，广义积分计算还需用到复变函数理论、级数理论、概率密度函数理论等多种方法不同角度解决，以达到全面有效解决实际问题。[1-3]

1 广义积分概念理论知识介绍

反常积分通常包含两大类型，第一类为积分区间为无穷的广义积分，第二类为无界函数的广义积分，其相关定义由以下给出。[4]

1.1 第一类广义积分

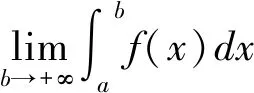
(1)

同理，可定义函数f(x)在区间(-∞,b]上的广义积分：

(2)

(3)

其中c为任意常数，当且仅当式(3)右边两个广义积分都收敛时称广义积分收敛，否则为发散。

1.2 第二类广义积分

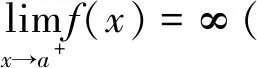
(4)

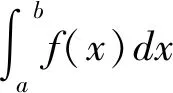
(5)

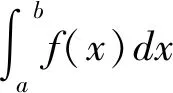
(6)

当且仅当式(6)右边两个广义积分都收敛时称广义积分收敛，否则为发散。

根据以上两类广义积分定义的特殊性，且计算灵活多变性的特点，反常积分的计算必然没有那么简单，不易掌握。为了有效解决反常积分，使其在工程计算中变得简单，本文根据相关理论知识给出几种计算反常积分得方法，并希望得以有效推广，使教学环节变得容易，开拓学生视野，使课堂教学应用更为简便。

2 广义积分几种计算方法解析

2.1 运用定义法计算广义积分

反常积分某种意义上是定积分的推广，因此，运用定义计算反常积分是最常见一种方法，也最容易被广大数学学子接受。根据定义计算，主要分两大步骤：第一求定积分，这关键依赖于不定积分计算准则；第二取极限，这主要运用极限计算法则。[5]这种计算方法格式相对固定统一，且理论已成型，只要计算准确即可。

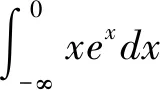
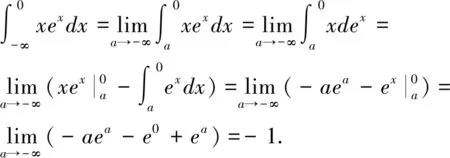
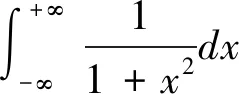
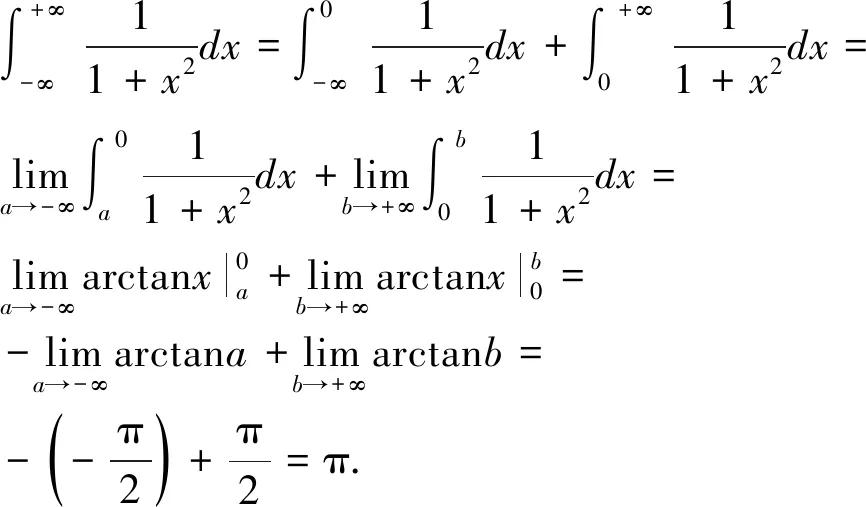
2.2 运用等量代换计算广义积分

对于某些特殊函数，根据定义对被积函数直接计算原函数，积分不容易求出，但是如果对被积函数进行恰当的等量代换，借助某种技巧，则就可以相对简便地求出原函数。注意的是，在进行等量代换时，不仅需要对被积函数结构进行分析，还得看积分上下限与被积函数关系，求得原函数，进而求出广义积分值。

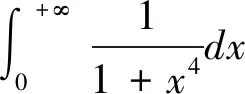
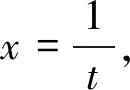
根据定积分定义知道，积分值与积分变量与字母无关，结合题目可以得出：

结合两式子，得出：

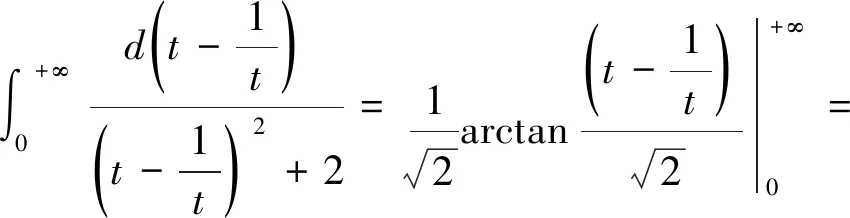
2.3 运用二重积分计算广义积分

对于部分特殊函数，如果根据不定积分求法可能无法求出原函数或者很难求出，这种情况就比较难处理。但是根据二重积分知识，则该类反常积分则可以通过巧妙方式化为计算二重积分，这样由二重积分得计算结果也就可以间接求出该反常积分值。

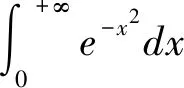
解：由定积分定义我们知道，积分值与积分变量，所以，有如下结果：

因此有结论：

这样，再结合极坐标变换得出：

而本文构造的反常与所求积分有如下关系：

因此题目所求积分值为：

2.4 运用拉普拉斯变换计算广义积分

对于多数广义积分而言，计算有的复杂有的简单。拉氏变换(Laplace)是一种将复杂运算化繁为简的方法。运用拉氏变换计算反常积分，可降低了计算难度，也有利于学者掌握，并且，对于多数函数而言，运用拉氏变换计算广义积分[6]，其结果可通过拉氏变换表查的，降低运算成本值得借鉴。

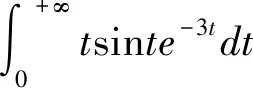
根据拉式变换微分性质，则有：

所以当p=3时，就是本例题多对应广义积分得解，即：

2.5 运用级数展开法计算广义积分

对于某些广义积分，直接求解比较复杂，需要某种技巧将其转化。有些实际问题，利用无穷级数计算广义积分也是常用的一种技巧，常用两种变化形式：一种是将被积函数展成级数[7]以求积分；另一种是将无穷区间上的广义积分表示成级数的形式[8]以求积分。

解：利用余弦函数的幂级数展开以及指数函数的展开式：

则有：

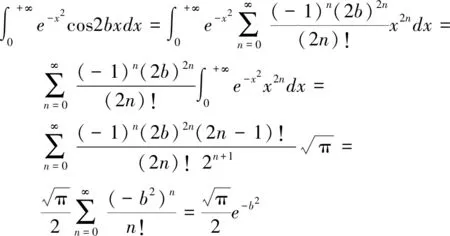
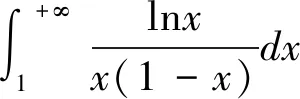
3 结 论

广义积分是积分学中一个重要知识点，也是一个难点，且广义积分在实际中应用很广，因此，目前对于广义积分计算方法研究，已呈现多种结论，且形式多种多样，是一个值得研究的课题。本文结合所学知识从5个不同角度分别给出5种不同的计算方法，有一定局限性，对于相同类实际问题可以有效解决，但对于某些问题，可能起不到好的效果，希望在后续研究中继续挖掘，争取在工程技术领域积分计算相关方面有所突破。