水下航行体垂直出筒时水锤压力分析与研究

李智生,刘 可,阎肖鹏

(中国人民解放军91550部队,辽宁大连116023)

0 引言

水下航行体采用弹射方式垂直出筒后，筒内的发射工质气体同时溢出发射筒，推开发射筒口附近的流体(水)向外运动，由于其惯性作用，致使发射筒内的压力下降，甚至低于平衡流体静压力值。这样，由于发射筒内、外压力差的作用，再加上水的重力作用，使涌入发射筒内的海水形似水锤冲向发射筒底，使筒内产生较大的压力，我们称它为水锤压力[1]。水锤压力对发射底部的结构强度和振动及发射平台的升沉均产生一定的影响，直接关系航行体发射的成败与否，所以对水锤压力研究具有重要的意义。

文献[2]采用CFD软件FLUENT对导弹离筒过程筒口气泡的发展及其对发射平台的影响进行了数值模拟，并给出了艇体不同位置压力脉动规律及其受发射深度的影响规律。文献[3]对不同出口速度条件下的筒口气泡脉动规律、作用在筒盖上的压强变化特性以及筒盖上的受载力矩时程进行了分析研究。文献[4]基于无相变VOF模型和动网格技术，采用二维轴对称模型，对潜射导弹筒口压力场特性进行了仿真分析。文献[5]分析了水下点火、发射方式和空泡过程三者之间的内在联系及其对出水弹道、水下航行体冲击振动的影响。通过分析，国内大多数专家研究集中于筒口压力场特性，对于水锤效应研究较少。本文以实测数据分析入手，对水锤压力现象、产生的机理，以及航行体离筒后海水倒灌后形成的水锤效应进行了研究，得到不同工况条件下水锤效应的变化规律。

1 基于水锤压力的机理分析

水锤效应的物理过程可以作如下描述[1]：

1)过程一。

设发射筒口至发射筒底高度为H，压缩波的传播速度为C，压缩波面由下往上传播，波面所到之处水流涌入速度降为0，但其压力却已升高。当时间t=H/C瞬时(时间t从海水到达筒底时起算)，波面到达发射筒口，这时发射筒内的水均受到压缩，水流速度均为0。

2)过程二。

由于筒口处波面上下两边的压力不等，筒内受压缩的水在压差的作用下，以一定的速度从发射筒内流出，即在H/C＜t＜2H/C的时间段内发射筒内形成膨胀波，膨胀波从上向下传播，波面所到之处，水中的压力就降至当地平衡水压并结束压缩状态。当t=2H/C瞬时，膨胀波到达筒底处，全发射筒内的水均不受压缩。这时正如一个受压缩的弹簧一样，当筒底处的水结束受压状态以后，由于惯性而具有一定速度的水继续向上流动，同时产生过度膨胀，筒内水中压力继续降低，筒底处的压力首先降为最低值，而产生一个新的膨胀波。

3)过程三。

在2H/C＜t＜3H/C的时间段内，新的膨胀波从下向上传播至筒口，这时筒内的压力均低于当地平衡水压。当t=3H/C瞬时，新的膨胀波到达筒口，波面上、下压力不等，筒内的压力低于筒外的压力，因而水流又开始涌入发射筒内，又产生一个新的压缩波。

4)过程四。

在3H/C＜t＜4H/C时间段内，这个新的压缩波又从上向下传播。当t=4H/C瞬时，新的压缩波到达发射筒底，水流仍以一定的速度冲向发射筒底，与t=0时的情况一样。

于是又重复上述的4个过程，如此循环下去。由于当筒内水压力增大时，不仅水是可压缩的，而且发射筒也是能变形的，这样必然要消耗一部分能量，而且在水流动过程中也必然要消耗能量。因此，水锤压力脉动是一种衰减振荡的形式。水锤压力也常伴随发射筒振动，这种振动虽然很快就衰减，但水锤压力的大小却是一个不容忽视的因素。

2 水锤压力特性

为了分析海水倒灌涌入并在发射筒底部产生冲击的详细过程，采用CFD计算方法，对航行体离筒后海水涌入发射筒后的流场特性和载荷特性进行分析。

2.1 流场特性

设定一定工况条件，图1给出了不同时刻发射筒内气水混合流场的密度云图、压力云图和速度云图。

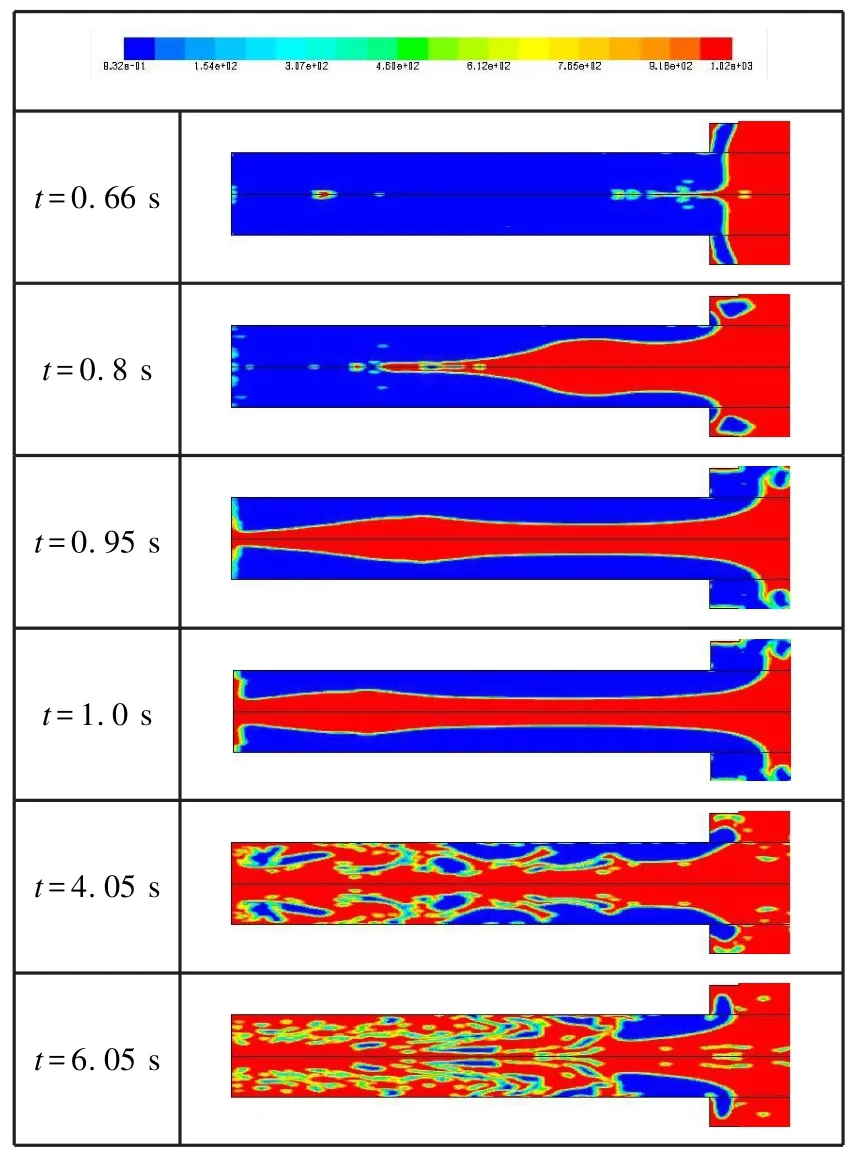
图1 密度云图Fig.1 Density nephogram

图2 压力云图Fig.2 Pressure nephogram

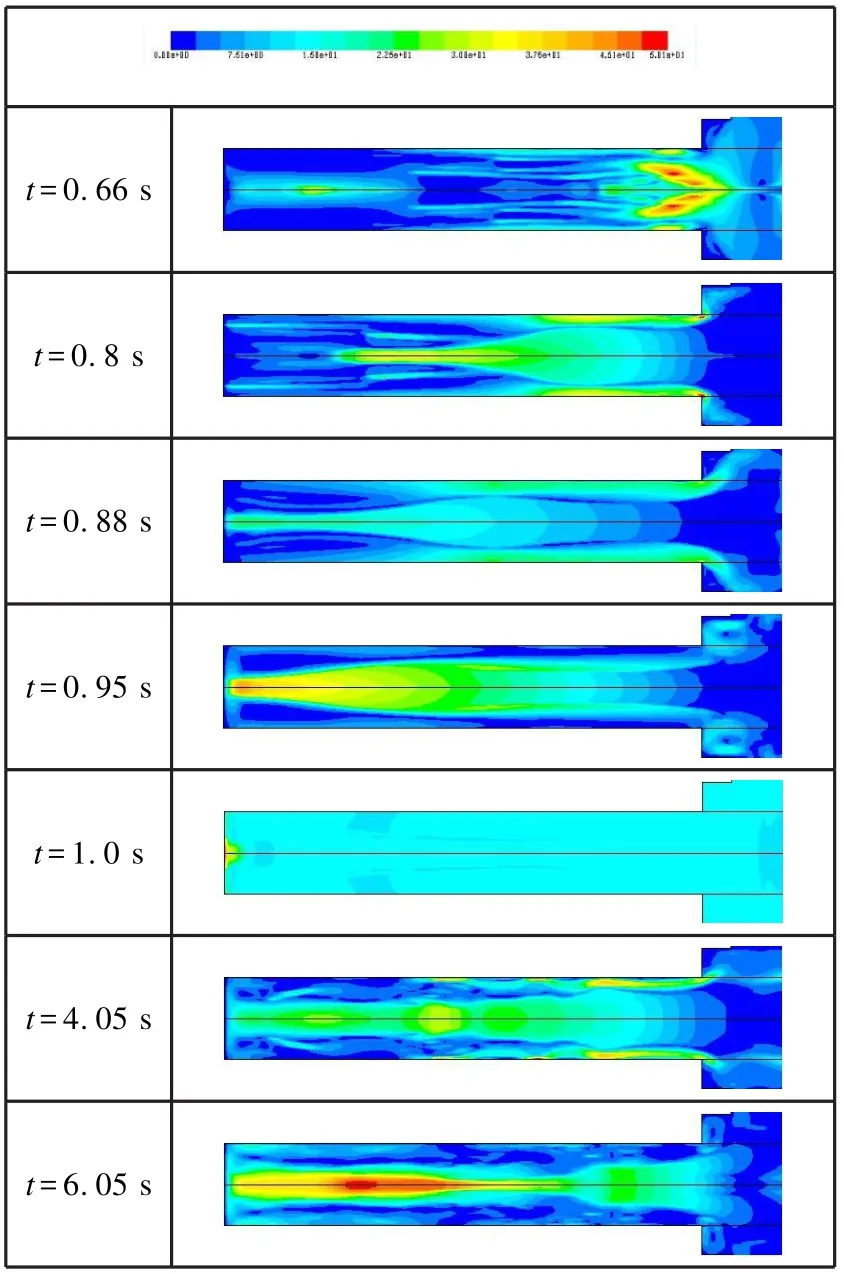
图3 速度云图Fig.3 Speed nephogram

图1中可以看到，在t=0.66 s时刻，海水首先从发射筒轴线附近区域开始涌入，在t=0.88 s时刻左右，沿中心处的海水，率先抵达发射筒底部区域，其间伴随着气泡的运动。在海水到达筒底后，由于水流受到发射筒底板的导流作用，开始向筒壁两侧发展，在t=1 s时刻，已经到达发射筒的侧壁面。由于海水的涌入，发射筒内剩余的气体“包裹”在水环境中，不断地被分割，挤压，最后排出筒内。这一过程中，受发射筒底部和筒内气体影响，海水冲击效应并不明显。

图2中可以看出，在t=0.88 s时刻，海水涌入筒底时，出现高压区，这是由于海水对筒底的冲击作用。随着海水向筒壁两侧发展，靠近壁面的区域出现高压区，这是因为海水挤压气体，使相对应区域的压力上升。

图3可以看出，各个时刻大量海水抵达发射筒底部时，受到发射筒底部阻滞，涌入海水的速度迅速降低，相应的压强快速升高，形成显著的压强冲击。

2.2 发射筒受载特性

1)压力监测点布置。

本文模拟计算的发射装置为单筒，简化为一个没有壁厚的圆柱筒[2]。海水倒灌过程中，筒内承受较大的载荷，且在不同截面处的载荷不同，为了研究其规律性，因此在发射筒内布置多个测点。计算为轴对称，此处模型为半模，在筒底中心布置11个压力测点。

2)压力曲线特性。

图4和图5分别给出了发射过程中筒壁面、筒中心监测点压力变化，各个监测点压力变化规律基本一致，且具有脉动特性。在0.4 s内，发射筒内气体处于膨胀状态，各监测点的压力变化基本一致，且压力值处于衰减阶段，随着航行体的运动；在0.4 s左右，空泡被拉断，“包裹”在筒口的气泡开始收缩，进而筒内的压力逐渐上升，各个监测点的压力开始升高，上升特性基本一致；在0.88 s时刻后，海水到达筒底，将剩余气体挤向筒壁，最后气体与筒外相通，压力开始缓慢下降，随后压力出现复杂的脉动规律，而且峰值不固定；在1.6 s以后，压力趋于当地水深压力。

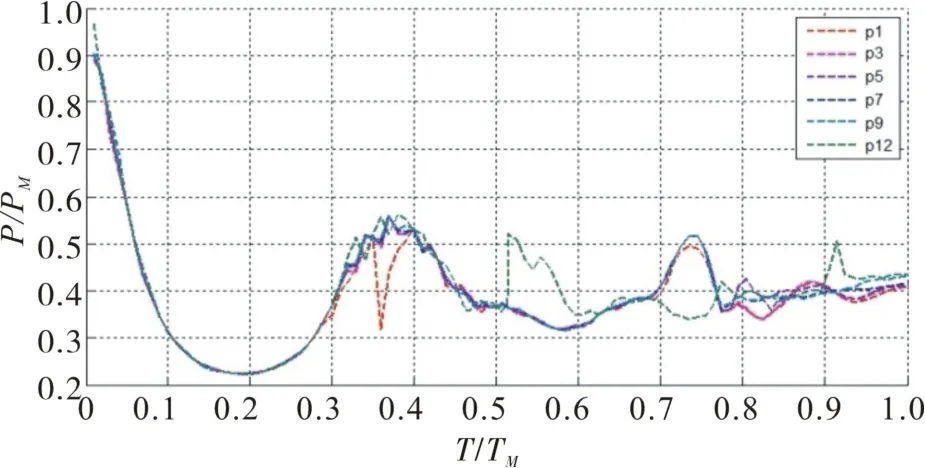
图4 壁面监测点压力随时间变化规律Fig.4 Variation of wallmonitoring point pressure With time

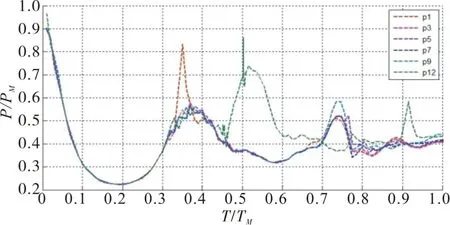
图5 发射筒中心处监测点压力随时间变化规律Fig.5 Variation of pressure antmonitoring point at center of launch tube with time

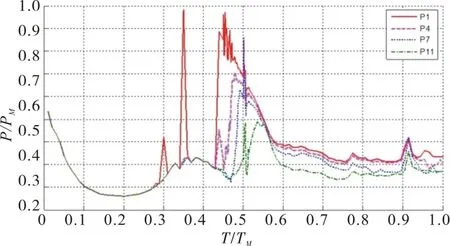
图6 发射筒底监测点压力随时间变化规律Fig.6 Variation of pressure atmonitoring point of bottom of launching tube With time

图6中给出了筒底各个监测点压力变化规律。结合图1密度云图可以看，“水锤”压力第一个峰值大约出现在1 s时刻附近，此时大量海水涌入筒底，对筒底产生很大冲击；随后筒底压力变化平缓，逐渐趋于当地静压值；随着远离发射筒底中心位置，测点压力值峰值出现滞后，此刻压力脉动是由于海水涌入筒底，从筒中心向两侧流动，挤压筒内气体所致。

2.3 水锤压力与筒口压力场的关联性

为了研究筒口压力场与筒底“水锤”压力的关系，我们提取了筒口中心处压力和发射筒底部中心压力来分析二者之间的关联性。图7给出了筒口中心压力和筒底中心压力随时间变化规律(图中坐标值进行了无量纲化处理)。

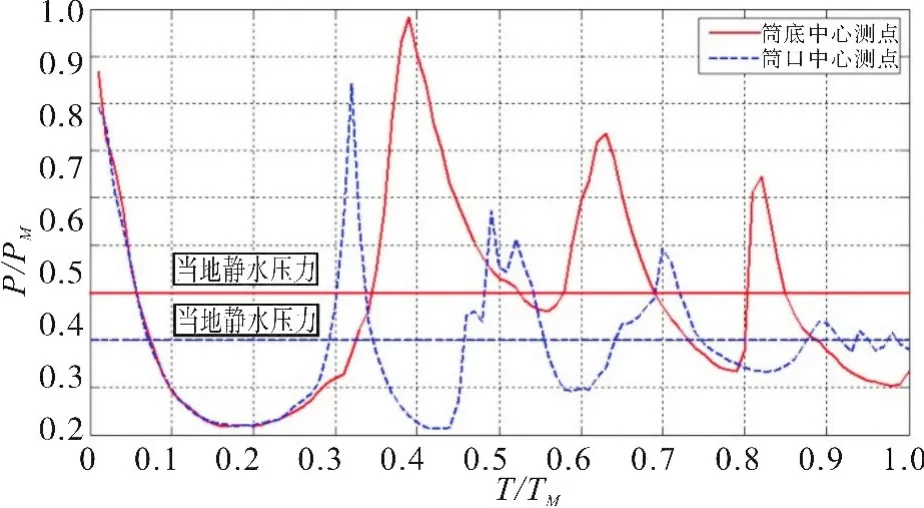
图7 测点压力随时间变化规律Fig.7 Pressure of measuring point changesWith time

起初，筒口中心和发射筒底部中心压力保持相同的变化趋势，随着气泡形态变化过程中的能量损失，压力急剧下降；气泡中部开始拉断时，弹尾气泡被压缩，泡内压力开始上升，筒口处的压力率先上升；随后筒口中心和筒底中心都出现了周期性压力脉动，脉动规律呈步调相反，即同一时间段内，波峰对于波谷，这也证明了当筒底出现压缩波(压力增大)时，筒口出现的是膨胀波(压力减小)，最终压力值回归到当地静水压力。

3 水锤压力影响因素研究

筒底水锤压力的第一峰值可以作如下估算[7-8]：设水流以速度V冲击到发射筒底，由于水流波被筒底挡住，紧贴筒底一层薄薄的水体立即停止流动，流速即为0；与此同时，该薄层水体上边来的水流，由于惯性仍以速度V继续流向发射筒底，冲挤该薄层并使之被压缩，该薄层水流的压力增加，即由原来的P0增至P0+P；然而该薄层的上侧压力仍然为P0。根据在Δt时间内该薄层流体的动量变化与其作用于该流层的外力合力的关系，可以用其流层轴线方向的冲量与动量增量的相等关系表示，即：

从中求出水锤压力第一峰值的表达式[1，6]，即：

则水锤压力第一峰值对筒底的压力估算公式为

式中：P0表示发射筒底部当地压强；ρ为海水密度；c为海水中压缩波传播速度，近似为海水中的声速；V为海水抵达发射筒底部时的速度；α为修正系数。

对于海水抵达发射筒底部时的速度，会受到航行体离筒后筒内外压差、发射筒长度以及两相之间非定常流动等因素的影响，为此，本文通过计算航行体离筒速度和离筒时筒内压力变化而反映发射筒底部压力的变化规律和特点。

3.1 初始压强影响

分别给定2种不同的初始燃气压强，其余计算条件保持不变。发射筒底部压力变化情况如图8所示(图中量值进行了无量纲化处理)。

由此可见：航行体离筒时刻筒内初始压力越大，“水锤”压力第一峰值越大，且随后的脉动峰值较大，达到压力峰值时间滞后。

3.2 航行体出筒速度影响

分别给定2种不同的航行体离筒速度，其余计算条件保持不变，发射筒底部压力变化情况如图9所示(图中量值进行了无量纲化处理)。

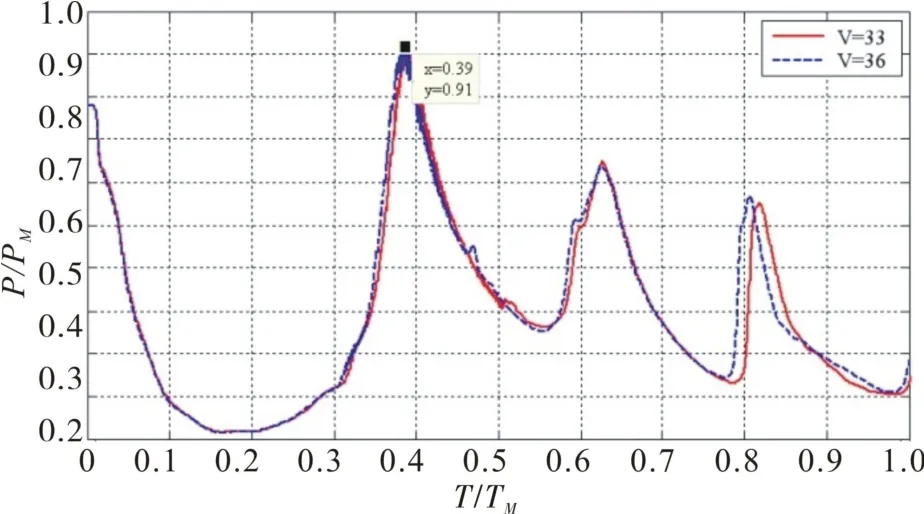
图9 发射筒底部压力-时间历程Fig.9 Pressure-time course at bottom of launch tube

不同出筒速度对“水锤”压力第一峰值影响较小，但是速度越大，出现峰值时间越提前。

4 结束语

本文建立了水锤压力峰值估算模型，采用CFD数值计算了海水涌入发射筒后的流场特性和载荷特性，得到了不同工况条件下航行体离筒后海水倒灌后形成的水锤效应变化规律，为发射装置的降噪、减振，以及如何减少航行体发射时对发射平台的安全性影响提供了方法和依据。