马尾松毛虫灾情指数的方差分析周期外推预报
2019-06-27余燕张书平毕守东
余燕 张书平 毕守东

摘要 为了提高马尾松毛虫Dendrolimus punctatus Walker灾情预报结果的准确性,为提高防治效果提供科学依据, 本文采用方差分析周期外推预报法,以安徽省潜山县的马尾松毛虫各代幼虫累计发生量和当代发生面积计算求得的灾情指数为依据,进行方差分析周期外推预报,并对预报结果进行验证。预报结果的历史符合率,1989-2016年全年灾情指数预报结果历史符合率为89.29%;预报2017年的结果与实况一致。1989-2016年的越冬代历史符合率为89.29%,2017年预报值与实际完全一致。1997-2016年的一代预报结果历史符合率为100%。1989-2016年的二代预报结果的历史符合率为85.19%。2017年由于越冬代飞防使用灭幼脲,使当年一、二代蟲口大幅度降低,预报值高于实况。方差分析周期外推预报法对马尾松毛虫的灾情指数预报是一种较理想的预报方法。
关键词 马尾松毛虫幼虫; 灾情指数; 方差分析周期外推预报
中图分类号: S 431.2
文献标识码: ADOI: 10.16688/j.zwbh.2018328
Abstract In order to improve the accuracy of disaster forecast of Dendrolimus punctatus, and provide scientific basis for improving the control efficacy, the periodic extrapolation prediction method of variance analysis was performed on the basis of the damage index calculated by the cumulative amount of larvae and the area of occurrence in each generation of D.punctatus in Qianshan county, Anhui province, and the prediction results were verified. The historical conformity rate of the annual disaster index forecast results was 89.29% for 1989-2016, and the forecasts for 2017 were in line with the actual data. The historical conformity rates of the overwintering and 2nd generations were 89.29% and 85.19% for 1989-2016, respectively, and the forecasts were in line with the actual data for 2017, while the historical conformity rate of the 1st generation was 100% in 1997-2016. In 2017, due to the application of chlorbenzuron by aerial spraying, the 1st and 2nd generations were greatly reduced and the forecast value was higher than the actual value. The method of variance analysis and periodic extrapolation is an ideal method for predicting the occurrence of D.punctatus.
Key words Dendrolimus punctatus larvae; damage index; analysis of variance periodic extrapolation prediction
马尾松毛虫Dendrolimus punctatus Walker分布于皖、豫、川、黔、陕、滇、赣、苏、湘、浙、闽、粤、琼、桂和台湾等省,主要为害马尾松Pinus massoniana Lamb.,还为害黑松P.thunbergii Parl.、火炬松P.taeda Linn.、湿地松 P.elliottii Engelm.、晚松P.rigida var. serotina (Michxa) Loud ex Hoopes、海南松P.fenzeliana Hand.Mazz.等松属植物。20世纪中叶马尾松毛虫是我国发生最广、危害面积最大,经常猖獗成灾的森林害虫。该虫不但影响林业生产,还危害人体健康[14]。进入21世纪,森林管理上采用了封山育林、混交、间作等措施,优化了森林生态系统,增加了物种多样性以及科学地运用综合治理措施,使马尾松毛虫的危害得到有效控制,但该虫具有巨大的繁殖潜能,遇到有利条件极易暴发成灾,对其监测丝毫不能放松。
马尾松毛虫一年发生2~4代,发生世代的多少随不同地区而异。马尾松毛虫发生的预测预报是对其进行综合防治的基本工作;森林保护工作者分别采用不同的预测方法预测马尾松毛虫的发生量、虫害等级以及发生类别、发生空间格局,为马尾松毛虫的综合防治工作提供了有力支持[515]。由于各地气象条件、植被条件和地形地貌的差异,马尾松毛虫的发生特点也不完全相同。对安徽省潜山县马尾松毛虫1983-2016年的各世代幼虫为害的灾情指数鲜见有具体的系统研究报道,本研究采用方差分析周期外推预报法预报马尾松毛虫幼虫为害的灾情指数,以期为马尾松毛虫的综合治理提供科学依据。
1 材料与方法
1.1 材料来源
马尾松毛虫资料来自国家林业局的森林病虫中心测报点——安徽省潜山县森林病虫防治站,资料的时间跨度为1983-2016年。根据国家林业局森林病虫防治总站制定的调查方法[16]进行调查,即采用踏查和详查相结合的方法,对不同虫态采取不同的观测方法。沿林斑线、林道、公路、铁路等线路调查,目测发生范围、为害状况,发现虫情或灾情立即设临时标准地,采取平行线抽样法抽取20株标准株详查。卵期调查是在雌蛾羽化高峰后1~2 d调查平均卵块数,卵块平均粒数;幼虫期调查,1~2龄幼虫调查枯黄卷曲的枝数,推算幼虫数,3龄以上的幼虫3 m以下的小树直接调查合计树冠上的幼虫数,大树用“虫粪粒推算法”调查,幼虫越冬期间调查树干基部树皮缝中的幼虫数推算全部蟲口。蛹期调查,在结茧盛期后2~5 d剖茧,调查雌雄性比、平均雌蛹重、死亡率、寄生率;成虫期调查,在成虫羽化前2~3 d及羽化期用黑光灯诱集,统计其诱集量和雌雄性比。
1.2 灾情指数计算公式
为了便于分析马尾松毛虫幼虫为害严重程度,考虑世代累计幼虫虫口和当代发生面积两个因素,提出了利用灾情指数为依据进行分析。灾情指数:Z=xi×yi×nxk×yH×n×100%。xi为第i年某世代累计虫口,yi为第i年某世代马尾松毛虫发生面积,n为平均每公顷松树株数,k为某代或全年最大的虫口,H为最大的发生面积。潜山县松林面积为6.986 7万hm2,1983年以来发生最大面积的是1996年的二代,其发生面积为33 381.4 hm2,占全县松林面积的47.78%,最大虫口为1996年,二代为52.6头/株。灾情指数分为以下4级:Z≤15%,轻度发生;15.1%≤Z≤30%,中等发生;30.1%≤Z≤45%,重度发生;Z>45%,特大发生。
1.3 方差分析周期外推预报法
方差分析周期外推预报是时间序列分析方法的一种[1],吴劲松[18]、张梅等[19]、杨长登[20]、武汉中心气象台等[23]、康晓慧等[21]和Kwon等[22]将该法应用于气象、农业、物理等方面的预测。如果对某种害虫的灾情指数进行等时距观测,就得到一列观测值y1,y2,y3,…,yn,即时间序列。如果该序列存在着周期长度为T的周期振荡,则当把序列排成T个数值一行时,得到T列数值因为每一列的数值都是在周期振荡的同一位相观测到的,每列数值内即组内(如y1、yT+1、…、yKT+1)差异不大,而各列平均值之间即组间的差异则较大,即各列间的差异较各列内的大。即组间均方差大于组内均方差。反之,如果序列的周期长度为T,在排列观测值时不是按T个数值一行,而是按t(t≠T)个数值一行,得到t列数值,由于这t列数值中每一列都是由不同位相观测值组成的,所以,各列平均值间就不会有显著差异,利用以上原理,如果当我们不知道序列中是否存在周期振荡时,就可以取不同的t值(试测周期,t的最大值应取小于或等于N/2,N为样本数),将序列排列起来,用方差分析检验各列平均值之间是否存在显著差异,如果检测结果表明t取某些数值时,各列平均值间差异显著,则该序列为周期振荡序列,其周期长度为t。
在实际时序中常包括若干个周期,通常取最显著的(即F值最大的)试测周期作为第一周期,各列平均值作为第一周期分量。然后从原序列中减去第一周期分量,则得到第一周期余序列,对第一周期余序列继续进行方差分析,确定其中各列平均值差异最显著的周期为第二周期,相应各列平均值为第二周期分量。第一周期余序列减去第二周期分量,得到第二周期余序列,如此反复,重复试测周期,进行分析直到余序列没有显著周期时为止。预报时将各周期分量叠加,然后外延即可求出未来时段的灾情指数预报值。
2 结果与分析
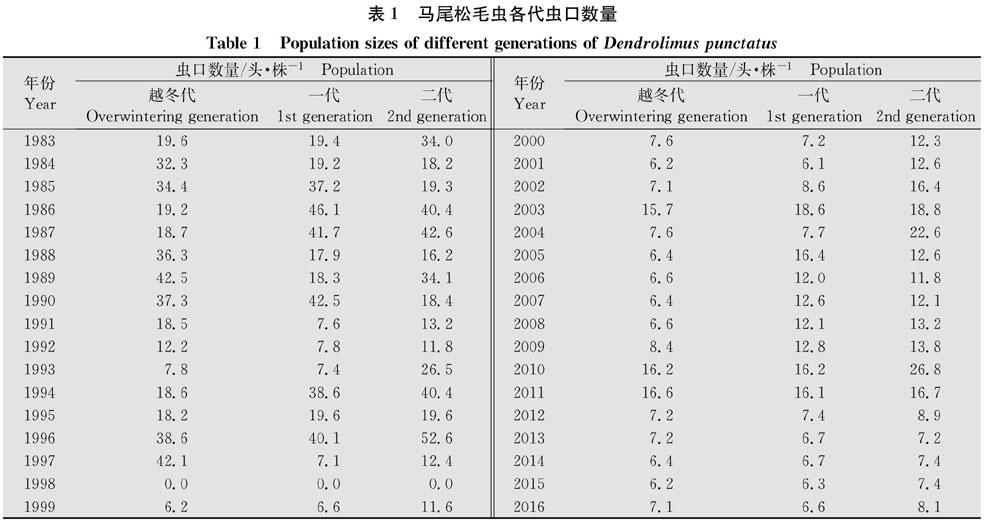
将潜山县1983-2016年越冬代幼虫累计虫口动态列于表1,其中1998年由于前两年马尾松毛虫暴发,用灭幼脲采取飞防措施导致该年没有发生,因此统计值为0,根据虫口变动特点,划分为1983-1998年和1999-2016年两个时段。越冬代幼虫1983-2016年虫口数量变动很大,1983-1998年除了1992年12.2头/株,1993年为7.8头/株和1998年0头/株外,其他年份都在12.2~42.1之间,1983-1998年平均达24.76头/株。1999-2016年虫口较低,18年平均8.43头/株。一代幼虫虫口数量变化与越冬代相似,1983-1998年除了1991、1992、1993、1997和1998年数量较少外,16年平均达23.16头/株,1999-2016年平均虫口为10.37头/株。二代幼虫虫口数量1983-1998年平均为24.98头/株,1999-2016年平均虫口为13.35头/株。总之1983-1997年各代幼虫累计虫口数量显著高于1999-2016年的虫口数量。
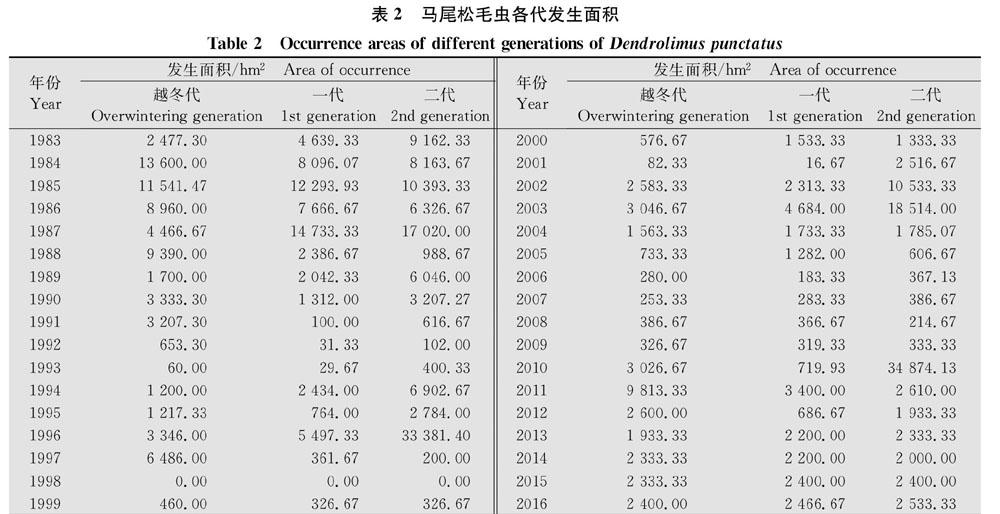
将1983-2016年马尾松毛虫的发生面积列于表2,1983-1998年和1999-2016年两个时段,各年各代发生面积差别很大。越冬代发生面积:1984年高达13 600 hm2,1985年为11 541.47 hm2。1983-1998年平均发生面积为4 477.42 hm2。1999-2016年19年平均发生面积为1 929.57 hm2。一代发生面积:1983-1998年发生面积较大的年份主要集中在1984-1987年,4年平均发生面积高达10 697.5 hm2。1983-1998年平均发生面积3 899.27 hm2,1999-2016年平均发生面积1 506.41 hm2。二代发生面积:1983-1998年之间发生面积大的年份是1983、1984、1985、1987和1996年,分别为9 162.33、8 163.67、10 393.33、17 020和33 381.4 hm2。16年平均发生面积为6 605.94 hm2。1999-2016年平均发生面积为4 755.65 hm2。这些波动都体现在周期振荡上。总之不管是发生面积还是各代幼虫累计虫口都是1983-1998年大,波动也大,1999-2016年的波动较小。由于波动幅度大小不一样,因此要对各时间段逐一进行周期试测。
2.1 全年的灾情指数动态
为了便于分析全年的马尾松毛虫灾情情况,将全年越冬代、一代、二代发生面积汇总,虫口数量采用越冬代、一代和二代之和的平均值。根据灾情指数公式,1983-2016年最大的全年累计发生面积为1996年的42 224.73 hm2,年度平均虫口最多的是1996年43.77头/株,两者之积作为全年灾情指数的分母,计算年度灾情指数列于表3,并绘于图1。
灾情指数大于45%的有1985年、1987年和1996年,属于特大发生年。灾情指数大于30%小于45%的有1984年、1986年和2010年,是重度发生年;灾情指数大于15%小于30%的有1983年、1988年、1989年、1994年和2003年,属于中度发生年;灾情指数均小于15%,属于轻发年,一共23年,占34年的67.65%,由于历史的原因,乱砍滥伐,森林生态系统遭到严重破坏,所以1983-1990年灾情指数一直很高。由于1992年、1993年全年平均虫口低,发生面积小,疏于防治,致使1994年和1995年虫口数量和发生面积都在上升,1996年大暴发,灾情指数达到100%。1996年和1997年两年连续飞防大大减小了1998年的灾情指数。进入21世纪以来由于采取了封山育林等一系列科学管理措施,优化了森林生态系统,使马尾松毛虫各代的虫口数量都较低。
根据图1反映的信息对1989年以来全年灾情指数进行周期试测,t=3,F=0.558;t=4,F=0.429;t=5,F=0.56;t=6,F=0.709;t=7,F=4.765;t=8,F=1.356;t=9,F=0.755;t=10,F=0.625;t=11,F=1.812;t=12,F=1.072;t=13,F=0.959;t=14,F=1.158。查F表,F0.01(df=6, 21)=3.81,只有t=7时,F>F0.01(6,21),组间差异极显著。将其第一周期t=7的周期分量列于表4,求得第一周期余序列也列于表4,对第一周期余序列继续周期试测,t=3,F=2.137;t=4,F=1.094;t=5,F=1.083;t=6,F=1.479;t=8,F=0.994;t=9,F=1.026;t=10,F=0.945;t=11,F=1.218;t=12,F=1.026;t=13,F=0.786;t=14,F=1.35,F值均小于F0.05,差异均不显著,经评判,1989年、1994年和2003年与实况不符,28年的历史符合率为89.29%。根据方差分析周期外推预测结果2017年为45.78%,2017年全年发生面积21 149.533 3 hm2,年平均虫口为5.033 3头/株,灾情指数实况为57.57%,预测结果与实况相符,均是特大发生年。
2.2 1989-2016年潜山县马尾松毛虫越冬代灾情指数
通过周期试测1989-2016年有周期振荡现象存在,越冬代最大虫口为1989年42.5头/株,越冬代最大发生面积为1984年13 600 hm2;将两者乘积作为灾情指数计算时的分母,将求得各年灾情指数列于表5,并绘于图2,进行周期试测,t=3,F=0.755;t=4,F=0.207;t=5,F=0.702;t=6,F=0.826;t=7,F=5.323;t=8,F=0.918;t=9,F=0.441;t=10,F=0.948;t=11,F=0.879;t=12,F=0.725;t=13,F=1.106,t=14,F=5.213。查F表,F0.01(6,21)=3.81,只有t=7时,F>F0.01(6,21),组间差异极显著。将其第一周期t=7的周期分量列于表5,求得第一周期余序列也列于表5,对第一周期余序列继续周期试测,t=3,F=1.577;t=4,F=0.662;t=5,F=1.647;t=6,F=1.381;t=8,F=0.498;t=9,F=0.93;t=10,F=1.196;t=11,F=1.102;t=12,F=0.813;t=13,F=0.478;t=14,F=1.429。t由3至12为周期,其F值均小于F0.05,表明第一周期余序列没有周期振荡现象存在,第一周期分量就是预报值,历史符合率为89.29%。2017年越冬代发生面积为5 521.47 hm2,发生虫口数量为12.8头/株,灾情指数为12.23%。2018年越冬代发生面积为5 790 hm2,发生虫口数量为1.8头/株,灾情指数为1.8%,预测灾情指数2017年为12.90%,2018年为24.75%,2017年预测值与实况相符,2018年预测值高一级,其原因是2017年越冬代进行了飞防,压低了2018年的虫口,使预测值大于实况值。
2.3 马尾松毛虫一代幼虫灾情指数
通过周期试测1997-2016年有周期振荡现象存在,一代最大虫口数量为1986年的46.1頭/株,一代最大发生面积为1987年的14 733.33 hm2。将两者乘积作为灾情指数计算时的分母,将求得的各年灾情指数列于表6,并绘于图3,进行周期试测,t=3时,F=0.529;t=4时,F=1.72;t=5时,F=0.488;t=6时,F=0.636;t=7时,F=1.393;t=8时,F=11.474;t=9时,F=1.242;t=10时,F=0.999。只有t=8为周期的F>F0.01(7,20)=3.7,t=8的周期分量和余序列也列于表6,继续对t=8为周期的余序列进行周期试测,t=3时,F=0.151;t=4,F=0;t=5,F=0.797;t=6,F=0.479;t=7,F=0.882;t=9,t=0.848;t=10,t=2.327。表明第一周期余序列的t为3、4、5、6、7、9、10时F值都小于F0.05,即没有周期振荡现象存在,第一周期分量就是预报值。对其进行评判,28年的历史符合率为100%。2017年一代发生面积为9 855.2 hm2,2017年一代虫口数量为1.2头/株,实际灾情指数2017年为1.74,预测外推结果依次为0.31。2018年发生面积为2 333.33 hm2,2018年虫口数量为1.6头/株,实际灾情指数2018年为0.5,预测外推结果为2.325。2017年和2018年灾情实况和预测值均为轻度发生,预报结果准确。
2.4 马尾松毛虫二代幼虫灾情指数预报
通过周期试测1989-2016年有周期振荡现象存在,二代最多虫口数量为1996年的52.6头/株,二代最大发生面积为1996年的33381.4 hm2。将两者乘积作为灾情指数的分母,求得的各年灾情指数列于表7,并绘于图4,进行周期试测,t=3,F=0.395;t=4,F=0.639;t=5,F=0.482;t=6,F=0.702;t=7,F=4.057;t=8,F=1.484;t=9,F=1.23;t=10,F=0.692;t=11,F=1.23;t=12,F=1.062;t=13,F=0.935;t=14,F=8.295。t为3、4、5、6、7、8、9、10、11、12、13、14时的F值只有t=14时,F>F0.01(13,14)=3.72,即差异极显著,对t=14周期的余序列继续进行周期试测,t=3,F=1.922;t=4,F=0.345;t=5,F=0.733;t=6,F=1.118;t=7,F=0;t=8,F=0.831;t=9,F=1.401;t=10,F=0.838;t=11,F=1.487;t=12,F=0.806;t=13,F=0.988。t为3、4、5、6、7、8、9、10、11、12、13时其F值均小于F0.05,表明第一周期余序列没有周期振荡存在,第一周期分量就是预报值。按照灾情指数的分级,历史符合率为100%,其中2003年和2010年为特大发生,其余均为轻度发生。2017年二代发生面积5 772.87 hm2,二代幼虫虫口数量1.1头/株,灾情指数为0.36,外推预测结果灾情指数为12.935,实况和预报值均为轻度发生,外推灾情指数高于实际发生的灾情指数。由于2017年越冬代飞防使用了灭幼脲,所以使当年二代虫口数量大幅下降,使实况灾情指数降低。1989年以来预测结果历史符合率为85.19%,只有1994、1996、2003和2010年的预测结果略低于实况。
3 小结与讨论
本文采用方差分析周期外推预报法以安徽省潜山县马尾松毛虫各代幼虫累计发生量和当代发生面积为依据计算灾情指数,对灾情指数进行周期试测,并对越冬代、一代、二代和全年的灾情指数预报值和实况值进行评判和比较,结果是越冬代的历史符合率为89.29%,2017年的预报值与实况一致。一代历史符合率为100%,二代的历史符合率为85.19%。2017年的预报值比实况高一级,全年灾情预报结果历史符合率为89.29%。方差分析周期外推预报法较之于BP神经网络法,马尔科夫链法,灾变预测法,列联表分析法优,计算方便,预报结果较准确,且计算时采用分析的数据不是其他生态因子数据,对一些与害虫发生有关的不易获取的生态因子数据,作为预报要素,这些数据与预报量有关时则不易进行预报,而方差分析周期外推预报法可以克服这些困难,但方差分析周期外推预报法法只适用于预报因子有周期振荡现象时的预报,这是其局限性。
对于一个县域范围总体上的虫害灾情评判,到目前为止还没有一个较理想的标准,特别是森林害虫。本文采用灾情指数,基于危害虫态的数量以及发生面积等因子计算灾情指数。本文是基于安徽省潜山县1983-2016年马尾松毛虫各代幼虫发生数量和发生面积的历史资料进行研究的,其他虫害也可参考此法,灾情指数通过外推可预报未来的发生严重程度,以便提前做好预防工作,变被动为主动,尽量减少虫害损失。本研究发现越冬代的振荡周期是7年,一代是8年,二代是14年,为什么三代的震荡周期不一致?分析其原因,可能主要包括:害虫的数量变化一是受气象等物理环境因素影响,二是受管理措施影响,三是受天敌的种类和数量多少影响,这三种因子对越冬代、一代、二代的作用可能是不一样的,因此出现越冬代、一代和二代的灾情指数振荡周期不一致的现象;其不同代幼虫受外界因素的具体影响情况以及马尾松毛虫响应的内在因素尚需开展系统研究。
参考文献
[1] 侯陶谦.中国松毛虫[M].北京:科学出版社,1987:188191.
[2] 邹运鼎,程扶玖,查光济.松针内含物与马尾松毛虫生存发育关系的研究[J].林业科学,1990,26(2):142148.
[3] 萧刚柔.中国森林害虫(第二版)[M].北京:林业出版社,1992:948953.
[4] 张真,李典谟.马尾松毛虫暴发机制分析[J].林业科学,2008,44(1):140150.
[5] 张爱兵,陈建,王正军,等.BP网络模型和LOGIT模型在森林害虫测报上的应用初报——以安徽省潜山县马尾松毛虫为例[J].生态学报,2001,21(12):21592165.
[6] PARK Y S,CEREGHINO R,COMPIN A. Applications of artificial neural networks for patterning and predicting aquatic insect species richness in running waters [J]. Ecological Modelling, 2003,160(3): 265280.
[7] 賈春生.利用马尔可夫链方法测报马尾松毛虫发生级别[J].东北林业大学学报, 2006, 34(5):2122.
[8] ZHANG W J,ZHONG X Q,LIU G H. Recognizing spatial distribution patterns of grassland insects: neural network approaches [J].Stochastic Environmental Research and Risk Assessment,2008, 22(2): 207216.
[9] 陈绘画,王坚娅,徐志宏.基于响应面方法的马尾松毛虫发生量混沌特性检测及其预测[J].东北林业大学学报,2011,39(9):9496.
[10]田万银,徐华潮.浙江沿海防护林马尾松毛虫的预测预报模型[J].环境昆虫学报,2012,34(4):401406.
[11]费海泽,王鸿斌,孔祥波等.马尾松毛虫发生相关气象因子筛选及预测[J].东北林业大学学报,2014,41(1):136140.
[12]许章华,李聪慧,刘健.马尾松毛虫害等级的Fisher判别分析[J].农业机械学报,2014,45(6):275283.
[13]王庆,毕猛,杜婷.基于气象因子的马尾松毛虫发生率空间格局研究[J].林业科学研究,2016,29(2):256260.
[14]余燕,李尚,王振兴,等.马尾松毛虫幼虫发生严重程度的预测研究[J].安徽农业大学学报,2017,44(5):882893.
[15]周夏芝,王振兴,余燕,等.马尾松毛虫幼虫高峰期发生量的预测模型研究[J].应用昆虫学报,2017,54(6):10311043.
[16]国家林业局森林病虫害防治总站.林业有害生物监测预报技术[J].北京:中国林业出版社,2013:117118.
[17]张孝羲,翟保平,牟极元,等.昆虫生态及预测预报[M].第3版.北京:中国农业出版社,2002:262265.
[18]吴劲松.用方差分析周期及随机时间序列法作赫章6-8月总降雨量预报[J].贵州气象,1999,23(1):1314.
[19]张梅,陈玉光,杨冰.方差分析周期叠加法预测农作物生长季积温[J].现代农业科技,2017(21):237240.
[20]杨长登.用方差分析周期叠加外推法预报年降水量[J].贵州气象,1998,22(1):2325.
[21]康晓慧,陈浩,张梅.3种时间序列分析模型在水稻稻瘟病预测中的应用[J].西北农林科技大学学报(自然科学版),2011,39(6):173184.
[22]KWON J H. Crystal graphs and the combinatorics of young tableaux [M]. Handbook of Algebra. Vol 6, NorthHolland, New York, 2009: 473504.
[23]武汉中心气象台,武汉大学数学系.方差分析周期外推法在長期预报中的应用[J].数学学报,1974,17(3):156163.
(责任编辑:田 喆)
