含风电系统中机组组合的分时段分层优化
2019-06-27林创
林创


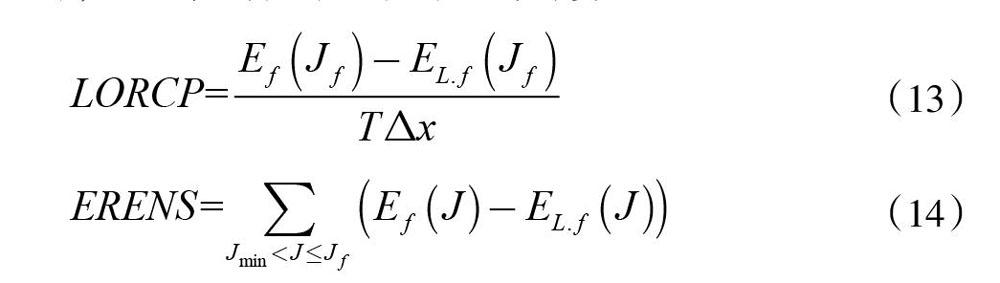
摘 要:首先,基于随机生产模拟算法(probabilistic production simulation algorithm,PPSA),建立了包含风电、火电、水电、气电和抽水蓄能等类型的机组组合优化模型,其特点是可通过PPSA提供的可靠性指标和灵活性指标形成约束,从而保证机组组合方案的优化必然满足可靠性和灵活性的要求;然后,以PSO、PL和动态规划三种算法构成分时段与分层的优化策略,对机组组合方案的经济性进行优化;最后,利用所提出的模型及策略对10机和32机系统的机组组合问题进行求解,验证了该方法的准确性和有效性。
关键词:随机生产模拟算法;机组组合;分时段优化;分層优化
中图分类号:TM614 文献标志码:A 文章编号:2095-2945(2019)10-0011-04
Abstract: Firstly, based on the probabilistic production simulation algorithm (PPSA), an optimization model of unit commitment is established, which includes wind power, thermal power, hydropower, gas power and pumped storage. Its characteristic is that the reliability index and flexibility index provided by PPSA can be used to form constraints, so as to ensure that the optimization of unit commitment scheme must meet the requirements of reliability and flexibility. Three algorithms, PSO, PL and dynamic programming, are used to form a time-division and hierarchical optimization strategy to optimize the economy of the unit commitment scheme. Finally, the proposed model and strategy are used to solve the unit commitment problem of 10-machine and 32-machine systems and the accuracy and effectiveness of the method are verified.
Keywords: probabilistic production simulation algorithm; unit commitment; time-interval optimization; layered optimization
引言
机组组合是实现电力系统安全运行和经济调度的基础环节,其主要目的是制定单目标最优或多目标整体较优的调度计划。近年来,随着风电等间歇性能源的大规模并网,机组组合问题中的不确定性显著增加,为电力系统的调度工作带来严峻挑战,一方面传统的机组组合问题求解模型无法有效地考虑风电的随机性与波动性,导致所得方案的适用性大打折扣,另一方面对于完备的求解模型,却缺乏精确且高效的优化算法,不利于实际的应用。
针对以上两个难点,国内外的专家学者们在此领域中开展了大量的研究。现有的机组组合模型主要依据风电的功率点预测[1][2]和场景生成[3][4]两种方法建立,但存在无法确定最优备用及运行点等难题。文献[5]关注了机组组合求解结果在任一瞬间之间的牵制问题,并建立了新的数学模型。文献[6]基于风电预测的SSCUC模型,将风电的不确定性模型分解为1个确定场景和2个极限场景,简化了求解复杂度。关于求解方法,混合整数非线性规划、动态规划[7]以及智能优化等算法[8]均在当前研究中有所应用,但单独的一种算法都具有局限性。
受上述思路及研究的启发,本文仍主要从机组组合模型的建立和优化算法的选择两方面开展研究。首先,鉴于已有的机组组合模型在生产中适用性较差,所以本文另辟蹊径,基于随机生产模拟算法(PPSA)的思想建立了机组组合的模型。历经长足的发展,目前的PPSA研究已能够考虑诸如负荷波动、机组停运、新能源出力波动等因素,基本具备分析评估系统运行计划的功能[9][10]。对于机组组合的优化方法,本文选择了动态规划、优先顺序(priority list,PL)和粒子群算法(particle swarm op-timization,PSO)三者相结合的方法进行求解。
1 机组模型
1.1 风电机组
本文采用如下的七参数混合Weibull分布描述风速[11],相比于两参数形式,多参数的混合Weibull分布对段周期内的风速拟合精度更高。
风电机组的出力函数与风速密切相关,且具有切入与切出风速的特点,式(4)所描述的风电出力特性较为经典可靠,且满足精度要求。
式中,Pw0为额定输出功率,vr为额定风速,vco为切出风速,vci为切入风速。
1.2 火电机组
火电机组正常运行时,需保证发电功率不低于规定的最小稳定出力,剩余容量因具有一定的调节能力可作为调峰或旋转备用,但机组受最大爬坡率约束,同时运行经济性下降。因此,火电机组的模型包含最小稳定出力和可调节出力两部分,后者还分为调峰容量和备用容量,并考虑爬坡约束及额外成本,如式(5)所示。
式中,Pt.u、Pt.f、Pt.a和Pt.s分别为单机容量、最小稳定出力、调峰出力和备用容量,Rt.f、Rt.s分别为最小稳定出力率和备用率,Tt.f和Tt.r分别为平均故障间隔时间和故障恢复时间,Rt.cv为最大爬坡率,Pg、Et.a和Et.c为模拟周期T内的平均出力和调峰、爬坡电量,△t为爬坡时间,Kt.c为爬坡惩罚系数,Ct.a为调峰发电的单位成本。
1.3 燃气轮机
与常规燃煤机组相比,燃气轮机的启停性能更好,且爬坡能力更强,但发电成本高,所以为兼顾经济性而仅作调峰电源使用。燃气轮机本质上是火电,出力模型与火电类似,但需要增加最大发电小时数Tmax体现“两班制”运行模式,如式(6)所示。
式中, Pp.u、Pp.f、Pp.a和Pp.s分别为调峰机组的单机容量、最小稳定出力、调峰出力和备用容量,Rp.f、Rp.s分别为最小稳定出力率和备用率,Ti为机组在各时段的发电时间。
1.4 抽水蓄能机组
运行于抽水工况下的抽蓄机组相当于电动机负荷,将从电网吸收的有功转化为水能进行储存,最大储存量由最大蓄水库容决定,而每小时的抽水量根据系统需求确定,模型如式(7)所示。
式中,Em.ps、Eps分别为抽水机组消耗的发电量和最大抽水库容所储存的水能,Pm.ps为抽水消耗的功率,Tps为抽水持续时间,?浊m为转化效率。
1.5 停机备用机组
处于停机备用状态的机组,主要考虑其启动费用对运行经济性的负面影响[12],以及最小停运时间和最小运行时间两项约束[13],模型如式(8)所示。
2 随机生产模擬算法
2.1 基本原理
在诸多的生产模拟算法之中,综合运算效率和精确度两方面,等效电量函数法(Equivalent energy function method, EEF)的表现更为优异[14],这是一种严格的算法,且计算速度快,本文的PPSA是基于EEF法进行设计。
等效电量函数根据式(9)定义。假设安排了i-1台机组后,已知E(i-1)(J),且第i台机组容量和随机停运率分别为Pi和qi,则E(i)(J)据式(10)计算[15]。
当系统含有n台机组,根据E(n)(J)可计算EENS(电力不足期望值,Expected Energy not Sup-plied)和LOLP (电力不足概率,Loss of Load Proba-bility),如式(11)和(12)所示。通过约束LOLP或EENS,可使机组组合方案满足系统的可靠性要求。
2.2 灵活性指标
在PPSA中,本文还基于EEF的思想引入两项用于评估系统灵活性的指标,分别为LORCP(调峰容量不足概率,Loss of Regulating Capacity Proba-bility)与ERENS(调峰电量不足期望值,Expected Regulating Energy Not Supplied),可根据式(13)和(14)进行计算。
3 优化策略
3.1 分时段优化
由于风电出力具有随机性和波动性的特点,同时大多数地区的负荷也表现为显著的峰谷特性,所以大规模的风电接入后,电力系统在每个时段的最优机组组合方案都会随着风电出力与负荷的波动而有所变化,并且由于火电开机费用高昂、停机机组受最小启停时间约束以及备用容量受最大爬坡速率影响等问题,各个时段之间的机组发电计划呈现更加复杂的牵制关系。因此,最优的机组发电方案随时间推移发生变化,所以分时段优化的过程借鉴了动态规划思想,考虑前后两个时段状态转移所产生的影响。另一方面,对于每个时段内的最优机组发电方案,本文综合利用了PL和PSO两种方法,其中PL为PSO指定了搜索方向,使PSO提高结果的最优性,并加快收敛速度。
3.2 分层优化
分层优化是针对调峰机组、抽水蓄能机组等调峰电源采取的策略,由于此类电源往往需要综合各个时段的可靠性和灵活性情况来安排发电计划,所以先对其余机组的组合方案进行第一层优化,再根据第一层优化后各项约束及目标的情况,对调峰电源是否安排开机,以及投入发电的机组数量和具体时段等问题进行第二层优化。另一方面,由于调峰电源的机组数量较多、单机容量较小,所以采取分层优化策略后,可以有效减小求解规模,同时这也有利于发挥调峰电源“削峰填谷”的运行特性。
3.3 优化流程
综合以上两种优化策略,得到完整的优化流程如图1所示,优化目标是在满足系统可靠性、灵活性约束以及各项机组运行约束的前提下,实现系统运行的经济性最优和最小化火电开机。
4 算例
算例部分的内容主要分为以下两个方面:首先,以文献[16]中10机系统的机组组合问题验证本文所用优化模型的准确性;然后借助IEEE RTS-86的32机系统说明本文完整优化流程在加入风电后的有效性和合理性。
4.1 模型校验
对文献[16]中10机系统的机组组合问题进行求解,所得结果与文献[16]的最优方案相同,并将该方案代入本文模型进行模拟,通过对比煤耗的计算结果验证优化模型的准确性,文献[16]与本文的结果分别为81245.5和81201.9吨标煤。由于本文的模型采用了线性化的机组煤耗曲线,所以计算结果呈现一定的差异,但差别仅为0.05%,可见本文基于PPSA所建立的机组组合模型具有较高的准确度。
4.2 含风电的机组组合优化
由于10机系统仅包含火电机组,无法体现本文组合优化模型对于含风电的复杂电力系统的适用性,所以采用IEEE RTS-86的32机系统测试本文完整的优化模型,系统和机组基本信息见文献[17],并接入250台单机容量为4MW的风电,Weibull分布参数见文献[18],缺电成本2000元/MWh,弃电成本1000元/MWh。
接入風电后,系统各时段的机组组合如表1所示,总运行成本为1150.9万元,若采用传统的PL法进行优化,总成本则为1274.5万元,可见本文方法具有更好的经济性。另一方面,与接入风电前最优机组组合方案的总成本1076.78万元相比,风电使系统的经济性下降,原因是风电的发电成本较高且火电启停频繁。为应对风电出力的随机性,燃气与抽水蓄能机组的开机数量和运行时段增加,目的是保证系统满足可靠性与灵活性约束。
5 结论
本文基于随机生产模拟的思想,结合PSO、PL和动态规划三种优化算法,提出了针对含风电电力系统的机组组合优化方法。经两个算例验证,可见本文所提优化模型的计算精确度较高,同时可以对含风电系统的机组组合方案进行有效的优化,优化结果反映出风电对发电安排的影响,亦即该方案可满足系统消纳风电电量的要求。与其它算法相比较,本文所建立的模型由于考虑了机组的随机停运、特殊机组的运行特性以及风电的出力波动性等因素而具有更高的合理性和实用性,为求解机组组合问题提供了新的思路。相比传统优化算法,本文的优化方法在求解速度上表现较差,后续工作可以进一步提升其计算性能。
参考文献:
[1]Chen C L. Optimal Wind-Thermal Generating Unit Commitment[J]. IEEE Transactions on Energy Conversion, 2008,23(1):273-280.
[2]周玮,彭昱,孙辉,等.含风电场的电力系统动态经济调度[J].中国电机工程学报,2009,29(25):13-18.
[3]王勇超,陈皓勇,禤培正,等.基于最优场景集的含多类型电源鲁棒调度[J].电网技术,2016,40(2):354-362.
[4]谢敏,闫圆圆,刘明波,等.含随机风电的大规模多目标机组组合问题的向量序优化方法[J].电网技术,2015(1).
[5]韩学山,李本新,李荣,等.应对风电间歇性的火电机组组合模型构建与分析方法[J].电网技术,2017(5).
[6]汪超群,韦化,吴思缘.计及风电不确定性的随机安全约束机组组合[J].电网技术,2017(05):66-74.
[7]Rouhi F. Unit Commitment in Power System by Combination of Dynamic Programming, Genetic Algorithm and Particle Swarm Op-timization[J]. Indian Journal of Science & Technology, 2014.
[8]Sun L, Zhang Y, Jiang C. A matrix real-coded genetic algorithm to the unit commitment problem[J]. Electric Power Systems Research, 2006,76(9-10):716-728.
[9]王锡凡.电力系统优化规划[M].水利电力出版社,1990.
[10]陈亚博,盛戈皞,黎建,等.含光伏和风电的电力系统随机生产模拟[J].电力系统及其自动化学报,2015,27(5).
[11]王松岩,于继来.短时风速概率分布的混合威布尔逼近方法[J].电力系统自动化,2010,34(6):89-93.
[12]韩学山,柳焯.考虑发电机组输出功率速度限制的最优机组组合[J].电网技术,1994(6):11-16.
[13]杨冬锋,周苏荃,鲍锋.风电并网系统低谷时段的调峰能力分析[J].电网技术,2014,38(6):1446-1451.
[14]李林川,王锡凡,王秀丽.基于等效电量函数法的互联电力系统随机生产模拟[J].中国电机工程学报,1996(3):180-184.
[15]王锡凡,王秀丽.随机生产模拟及其应用[J].电力系统自动化,2003,27(8):10-15.
[16]李整,谭文,秦金磊.一种用于机组组合问题的改进双重粒子群算法[J].中国电机工程学报,2012,32(25):189-195.
[17]Allan R N, Billinton R, Abdel-Gawad N M K. The IEEE Reliability Test System - Extensions to and Evaluation of the Generating Sys-tem[J]. Power Systems IEEE Transactions on, 1986,1(4):1-7.
[18]Karaki SH, Chedid RB, Ramadan R. Probabilistic performance assessment of autonomous solar-wind energy conversion sys-tems. IEEE Trans on Energy Conversion, 1999,14(3):766-772.
