改进GA优化BP神经网络的雷达信号识别

杨 洁, 弋佳东

(西安邮电大学 通信与信息工程学院， 陕西 西安 710121)

随着现代电子技术的飞速发展，多种用途的新体制雷达投入使用，雷达信号的密度和复杂程度都大幅度提高。雷达辐射源信号识别是电子对抗和电子战的重要环节，正确识别雷达信号可以帮助己方对目标雷达类型、载体、用途、威胁等级的识别，进而在现代战争中取得先机[1-2]。雷达信号调制类型的识别是辐射源信号识别的核心，其设计的关键技术是寻找到性能优良的特征量和分类器。

在过去的十几年里，雷达信号识别技术受到了极大的重视，得到广泛的研究并取得了一系列重要的进展。在理论上，雷达信号识别的方法主要是通过提取能有效表征辐射源信号特征，构建新的识别特征参数体系从而进行雷达信号识别。文献[3]通过奇异值分解降低噪声对雷达信号模糊函数图像的影响，进而提高雷达信号的识别率，其识别复杂度较高。文献[4-5]利用信号时频图像的奇异值作为雷达信号的识别特征，取得有一定的效果，但因为奇异值特征维数较多，提取较为复杂，影响分类器的分类识别。文献[6-8]通过提取信号的盒维数和信息维数特征作为分类识别特征，在信噪比较高情况下取得了不错的识别效果，但是，在信噪比较低情况下，其识别效果不好。文献[9]利用了多尺度小波熵和特征权重选择法，得到了较高的识别率，但该方法步骤较为繁琐复杂，不利于实际应用。文献[10]通过提取雷达信号的熵特征，再使用神经网络分类器实现雷达信号的分类识别，取得了一定的效果。但是，神经网络分类器初始的权值和阈值是随机的，极易陷入局部最优解，进而影响到雷达信号的识别率。而选用反向传播 (back propagation,BP)神经网络作为雷达信号的分类器，分类识别效果明显且适应性较强，但是存在迭代次数较多且收敛较慢，网络输出层依然会陷入局部最优解等缺点。为了克服上述缺点，本文拟提出一种遗传算法(genetic algorithm，GA)优化BP神经网络的雷达信号识别算法。考虑到遗传算法存在过早收敛和局部收敛性差的问题[11-12]，该算法通过改进遗传算法的适应度函数和交叉算子，并应用于BP神经网络的雷达信号识别中，以期提升雷达信号的识别率。

1 雷达信号分类识别模型

通常情况下，雷达信号分类识别模型主要包括预处理、特征提取和分类识别等3个部分,分类识别模型流程如图1所示。

图1 雷达信号识别流程

预处理主要包括把信号从时域变换到频域，再进行能量归一化和幅度归一化等，预处理的主要目的是降低噪声对信号的影响，便于对信号进行特征提取。特征提取是一种把信号从测量空间转化到特征空间的非线性变换，其目的是减少数据集信息和集中具有显著差异的信息，对预处理后的信号进行特征提取，可以得到雷达信号的脉内信息。本文选取差分近似熵、调和平均盒维数和信息维数等3个表现稳健的特征作为雷达信号识别的脉冲内部特征。分类识别是将选取的特征参数归入到不同的类别中，进而实现信号的分类识别。信号的分类识别主要是通过分类器来实现的，而神经网络分类器则是典型的也较为常用的分类器。

尽管神经网络分类器的研究取得了很多进展，并广泛地应用实际雷达信号识别中，但神经网络在理论上存在着收敛速度慢，极易陷入局部最优解等问题，因而影响识别精度。考虑到遗传算法作为具有全局搜索性能的算法，可以很好的解决这些问题。因此，本文通过对遗传算法中的适应度函数和交叉算子进行适当的改进，提升遗传算法寻优性能，进而使用改进的遗传算法优化BP神经网络来实现各种雷达信号的分类识别。

2 GA的改进

遗传算法是模拟生物进化论中的自然选择和遗传学机理的生物进化过程，通过编码、选择、交叉、变异、解码等操作，依靠不断地进化搜索最优解的方法。但标准的遗传算法易陷入局部极值且收敛速度慢，为此，本文通过改进遗传算法的适应度函数和交叉算子来提升算法寻优性能，下面将介绍具体改进方法。

2.1 染色体编码与适应度函数的改进

标准遗传算法采用二进制编码方式，但二进制编码会使得编码过长，维数增加，导致计算量成倍增加[13]。为此，本文采用实数编码方式，便于进行更大范围内的搜索，也可以缩短遗传算法的执行时间。

适应度表示染色体的适应程度，即优劣程度，而适应度函数可以决定染色体的好坏，使适应度高的染色体被保留，适应度低的染色体被淘汰。标准遗传算法用实际输出与预测值差的绝对值求和来作为遗传算法的适应度函数，但这样会使得误差过大，收敛速度变慢。为提高算法的收敛速度，尽快找到全局最优解，对适应度函数的如下改进。

定义种群适应度的平均值fa和方差σ分别为

(1)

(2)

式中：fj为染色体j的适应度值；M为种群规模。经过改进调整后染色体的适应度值f′j为

(3)

需要注意，调整后个体适应度f′j≥0。

适应度作为种群进化的依据在遗传算法中具有非常重要的地位，改进适应度函数得到种群中每个染色体的适应度值，进而进行选择操作。

2.2 选择算子

遗传算法常用的选择算法有精英保留策略、轮盘赌、启发式等多种选择方法，本文采用轮盘赌方法进行选择操作。根据染色体适应度比例的选择策略对种群的染色体进行选择，每个染色体被选中的概率为

(4)

其中

(5)

式中：Pj为染色体j的选择概率；Fj为轮盘赌方法的选择概率；n为选择算子系数。

通过式(5)计算出染色体适应度所占的比例大小，再利用式(4)求出选择概率。然后，选择概率较高的染色体，进行下一步的选择交叉操作。

2.3 交叉算子的改进

交叉操作是从种群中选择不同的染色体进行交叉组合形成新染色体，进而增加种群的多样性[14]。标准遗传算法的交叉算子影响了算法的效率，特别是在进化后期，可能会导致优良染色体的损失，因此，为了保留优良染色体，对交叉算子进行改进。改进的交叉算子操作为

(6)

(7)

式中：amj和anj分别表示第m和第n个染色体上的第j位基因；a′mj和a′nj交叉后第m和第n个染色体上的第j位基因；r为交叉系数，取值为[0,1]上的随机数。

通过改进的交叉算子后，可在进化后期避免优良染色体的损失，加快最优解的搜寻。

2.4 变异算子

(8)

其中f(g)定义为

f(g)=λ1(1-g/G)。

(9)

式中：a″kl为第k个染色体第l位进行变异后的基因；a′max和a′min分别为交叉后基因a′kl取值的上和下界；λ和λ1取值均为[0,1]上的随机数；g为当前进化次数；G为最大进化次数。

通过选择、交叉和变异操作，得到每一代中最佳的适应度值。当适应度值达到最优时，将得到的最佳染色体解码得到BP神经网络最优的初始权值和阈值。

3 改进GA优化BP神经网络

3.1 构建BP神经网络模型

BP神经网络作为人工神经网络的一种，具有实现任何复杂非线性映射的功能，这使得它特别适合求解内部机制复杂的问题，应用也较为广泛。经典的三层结构可以高效的处理信号的分类识别问题，为了进一步提高BP神经网络分类器的性能，使用上述改进的遗传算法去优化BP神经网络，以期得到更高的信号识别率。

3.2 算法步骤

下面将说明改进遗传算法优化BP神经网络的雷达信号识别的具体步骤。

步骤1对雷达信号进行预处理，分别提取信号的差分近似熵、调和平均盒维数和分形维数等3个特征。

步骤2确定神经网络输入层、隐层和输出层的数目，构建BP神经网络模型，再通过网络结构模型得到权值和阈值的个数。

步骤3将训练数据输入BP神经网络并对初始权值和阈值进行编码，利用改进的适应度函数求出染色体适应度值。

OECD：美国经济增长稳固，但潜在风险犹存。6月6日，经济合作与发展组织（OECD）发布美国经济调查报告称，美国经济正处于有记录以来最长的扩张周期之一，但面临的潜在风险仍然较多，包括：企业部门高杠杆率需当局加强监管，利差可能推动美元升值;美国与主要合作伙伴贸易紧张局势加剧，有可能影响全球供应链,并削弱长期增长;财政的中长期可持续性有待观察。

步骤4选择出适应度概率较高的个体并进行改进的交叉和变异操作，计算每一代中最佳的适应度值。

步骤5当适应度值随着进化次数的增加没有明显的变化或达到最大进化次数时，停止进化，将最佳染色体解码得到最优的初始权值和阈值，将赋给BP神经网络。

步骤6将雷达信号训练数据输入到优化的BP神经网络，进行训练并计算输出误差，利用梯度下降法对网络进行权值和阈值的更新。

步骤7将测试数据输入到优化的BP神经网络，当神经网络训练次数达到设定上限或者输出结果满足设定的误差精度时，停止识别，并输出分类识别的结果。

4 仿真实验

仿真采用典型的雷达辐射源信号，分别为线性调频信号(linear frequency modulation signal，LFM)、连续波信号(continuous wave signal，CW)、正弦调频信号(sine frequency modulation signal，SFM)、二项编码信号(binary phase shift keying signal，BPSK)、四项编码信号(quaternary phase shift keying signal，QPSK)、非线性调频信号(nonlinear frequency modulation signal，NLFM)和频移键控信号(frequency shift keying signal，FSK) 等7种，并分别对其进行分类识别。辐射源信号的载频均为10 MHz，采样频率为100 MHz,长度为256 个采样点，其中LFM信号带宽为5 MHz，SFM采用正弦波调制，BPSK信号采用7位Barker码，QPSK信号采用16位Frank码，NLFM信号采用三次方调频，FSK信号采用随机编码。实验中信号附加的噪声均为零均值的高斯白噪声，信噪比变化范围为-4 dB到10 dB，每类信号每隔2 dB产生300 组数据，随机选取200 组数据用于训练，其余的数据进行测试。因为提取了3个稳健的特征用于分类识别，而且雷达信号的种类为7类，所以BP神经网络输入节点数为3个，输出节点数为7个，设定隐层节点数为10个，最大训练次数为300次，误差为0.001。设定遗传算法的种群规模为50，最大进化次数为400，交叉概率选取0.80，变异概率取为0.05。

利用遗传算法优化BP神经网络(genetic algorithm optimization BP，GA-BP)和改进的遗传算法优化BP神经网络(improved genetic algorithm optimization BP，IGA-BP)对雷达信号进行分类识别时染色体适应度值随迭代次数的变化关系，其结果如图2所示。

图2 两种算法适应度和迭代次数的关系

从图2可知，IGA-BP在进化到230代时达到最优，而GA-BP在进化到270代时才达到最优，说明 IGA-BP的进化速度更快，性能更优。

分别利用BP、GA-BP和IGA-BP网络模型的训练结果如表1所示。从表中数据可见，相较于BP和GA-BP， IGA-BP网络的均方误差和平均绝对误差更小，而且IGA-BP所需的进化次数更少，说明IGA-BP网络更稳定，寻优性能更好。

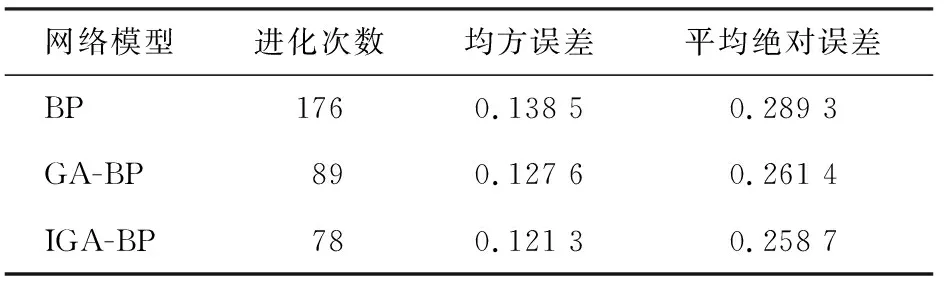
表1 实验误差

分别使用GA-BP和IGA-BP网络模型对7种典型的雷达辐射源信号进行分类识别，仿真结果分别如图3和图4所示。由图可知，在整个信噪比变化范围内，相比较于GA-BP，IGA-BP网络对7类雷达辐射源信号的识别率均到提升，尤其在低噪比情况下，IGA-BP网络雷达信号的识别率提升更加明显，由此说明该算法是有效的。

图3 GA-BP雷达辐射源信号识别结果

图4 IGA-BP雷达辐射源信号识别结果

图5给出了BP、GA-BP和IGA-BP等3种网络在不同信噪比下对7种雷达辐射源信号综合分类识别结果。结果看出，相比于BP和GA-BP，IGA-BP网络的识别概率更高，在信噪比为4dB时，所有信号的识别率为100%，而BP和GA-BP分别在8 dB和6 dB时，雷达信号的综合识别率才为100%，说明IGA-BP使得各类雷达信号的识别率得到提升，同时也具有更好的性能。

图5 雷达辐射源信号整体识别率

5 结语

针对雷达辐射源信号识别率低的问题，提出了一种改进遗传算法优化BP神经网络的雷达信号识别算法。该算法通过改进遗传算法中的适应度函数和交叉算子，在提取雷达信号差分近似熵、调和平均盒维数、信息维数等3个表现稳健特征的基础上，并用改进GA获取BP神经网络最优的初始权值和阈值，从而进行雷达辐射源信号识别。仿真结果表明,与BP、GA-BP网络对雷达信号进行识别算法相比， IGA-BP网络能有效提高雷达信号识别率并加快网络收敛速度，提升了算法的寻优性能。