振动筛不同运动形式对颗粒群筛分的影响

2019-06-27王立军崔友强郑招辉沈宝山李义博

农业机械学报 2019年6期

王立军崔友强郑招辉冯鑫沈宝山李义博

(1.东北农业大学工程学院，哈尔滨 150030； 2.黑龙江农垦八五二农场，双鸭山 155600)

0 引言

清选装置是收获机的重要组成部分,直接影响到整机的工作性能。物料在筛面上的运动形式对清选装置的筛分效率具有重要影响[1-6]。振动筛在作业时，颗粒群在筛面上的分散程度直接影响物料的分层与透筛，进而影响振动筛的筛分效率[7]。因此，研究筛分过程中物料的分散程度具有重要意义。

王成军等[8]基于离散元法对棉籽颗粒群，在三自由度振动筛筛面上的筛分过程进行了模拟分析，得出筛面的三自由度振动利于颗粒物料在筛面上的分散。马履中等[9]利用LS-DYNA程序，对往复式和两种新型多维运动振动筛筛面上的颗粒运动进行了模拟研究，并对3种筛面上颗粒的分散情况进行了对比。赵跃民等[10]通过对矩形振动盒内颗粒群的运动状态进行离散元模拟，得出计算参数对离散元法模拟结果的影响。刘琼[11]构造了三自由度混联激振机构，基于EDEM对棉花颗粒群在三自由度振动筛筛面上的筛分过程进行模拟分析。刘初升等[12-13]利用单颗粒在筛面上运动的非线性动力学模型，对颗粒周期运动进行稳定性分析，并对颗粒非线性运动规律进行讨论。WANG等[7]基于颗粒的非线性跳动理论，以平面往复振动筛为试验平台，模拟出玉米颗粒沿筛面长度方向不同位置处的运动规律。沈惠平等[14-15]利用并联振动筛和直线筛试验样机进行对比试验，提出用透筛率和筛分效率衡量筛分效果，然后从同量物料的完全筛分及在不同时间段内筛分两方面进行试验比较。李菊等[16-17]在不考虑气流作用的情况下，分别基于平面筛面和凸柱筛面的直线振动筛和并联振动筛进行筛分试验，得出凸柱筛面的并联振动筛有利于提高谷物的筛分效率和透筛率。PAUL等[18]运用EDM离散法研究了大型双层香蕉筛，探索该装置内颗粒流动特性，并获得了筛分性能与物料流动性的关系。

目前，研究者对于不同振动筛筛面上颗粒群分散度的研究主要以仿真研究为主，而对颗粒群在不同筛面上的分散性进行试验的研究鲜有报道，且忽略了气流的作用。谷物清选装置中振动筛的运动形式和气流的作用均会对颗粒群的分散度产生影响，在初始气流相同的情况下，由于振动筛的运动情况不同，每种振动筛筛上空间气流分布不同，气流对颗粒的作用效果不同，通过台架试验调节风机流量也很难实现不同振动筛筛上气流场分布相同。基于上述原因，本文研究振动筛的运动形式对颗粒群分散度的影响，在3种振动筛筛面颗粒非线性跳动理论分析的基础上，以3种运动形式的振动筛为研究平台，利用高速摄像对颗粒群分散性进行跟踪，观察颗粒群在振动平板上的实际分散情况，并进行筛面物料筛分验证试验，从而对比分析不同运动形式振动筛的筛分性能，为不同振动筛的选用及新型振动筛的设计与应用提供参考依据。

1 振动筛机构与工作原理

目前，平面往复振动筛的理论相对比较成熟，故玉米清选装置中的振动筛主要采用平面往复振动筛，但其运动形式简单，不易于颗粒群在筛面上的分散。很多专家提出了多维运动振动筛，可使颗粒群在筛面上实现快速分散，本文对以下3种振动筛进行研究。

1.1 平面往复振动筛

平面往复振动筛主要由上筛、连杆、曲柄、下筛、上吊杆、下支撑杆等组成，如图1所示。在电机驱动下，曲柄做匀速圆周运动，带动连杆做周期性运动；通过连杆与上吊杆和下支撑杆的作用，带动上筛和下筛做周期性运动，使颗粒在筛面以一定速度上滑、下移、抛起或透筛，上滑的距离大于下移的距离，保证了颗粒由筛面前端运动到筛面尾部，从而实现振动筛的平面往复振动[7]。

图1 平面往复振动筛模型Fig.1 Model of plane reciprocating vibrating screen1.上筛 2.连杆A 3.连杆B 4.曲柄 5.下支撑杆 6.下筛 7.上吊杆 8.机架

1.2 三移动一摆动振动筛

三移动一摆动振动筛主要由机架、侧板、滑道、连杆、偏心轮、下支撑杆、筛面、上吊杆等组成，如图2所示。在电机驱动下，偏心轮转动带动连杆摆动使滑块在滑道内往复运动，滑道内槽底部与筛面侧板不平行，故滑块在滑道内上下滑动时，使筛面实现沿x、y、z方向的移动。筛面后端通过上吊杆铰接固定在筛架上，筛面前端与滑块铰接，筛面随着滑块在滑道内上下滑移，由于筛面前后的铰接固定端分布于筛面的上下两侧，因而能够实现筛面围绕z轴摆动,从而实现3个方向的移动和1个方向的摆动。

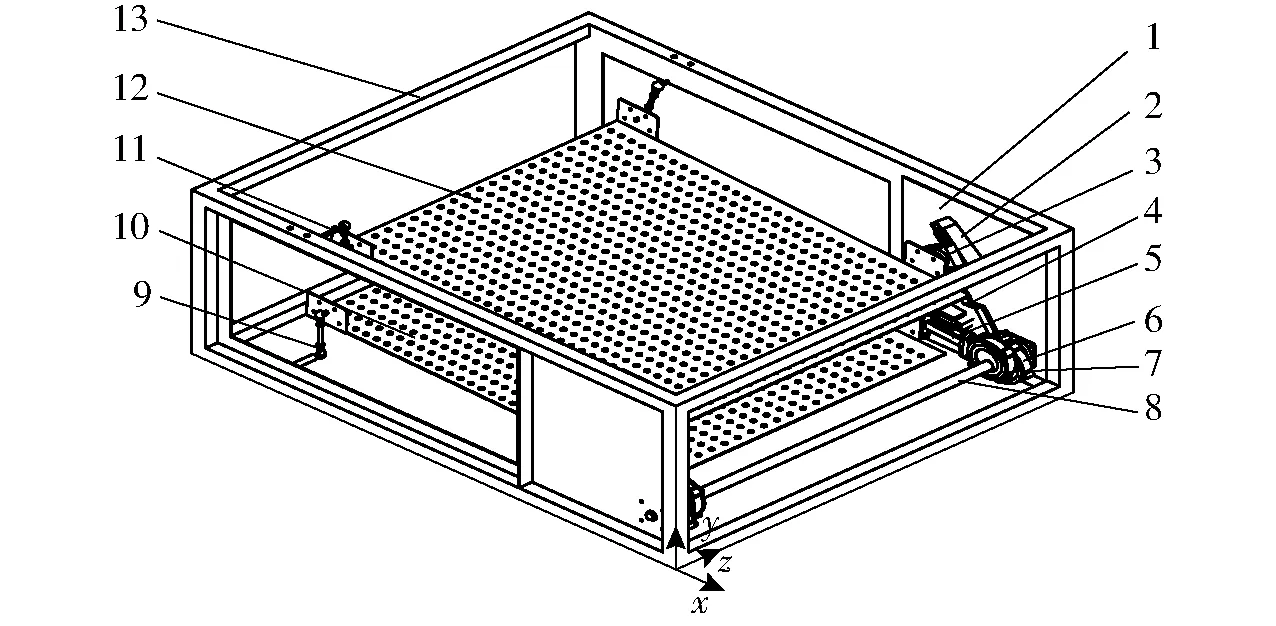
图2 三移动一摆动振动筛模型Fig.2 Model of vibrating screen with three translations and one swing1.侧板 2.滑道 3.滑块 4.连杆A 5.连杆B 6.偏心轮A 7.偏心轮B 8.主轴 9.下支撑杆 10.下筛 11.上吊杆 12.上筛 13.机架

1.3 三移动两转动振动筛

三移动两转动振动筛主要由上筛、机架、导杆、限位杆、V型杆、T型杆、偏心轮、连杆、摇杆、吊杆、球铰等组成，如图3所示。在电机驱动下，偏心轮转动带动连杆使摇杆摆动，使筛面实现沿x、y方向的移动。筛面前后的铰接固定端分布于筛面的上下两侧，在筛面沿x、y方向移动时，会产生一个附加的转动，因而能够实现筛面围绕z轴转动；机构左右两侧限位杆铰接位置的不对称布置，使筛面两侧导杆在摇杆的牵引作用下不同步运动，进而实现筛面绕x轴转动；限制左侧活动连杆绕x轴转动，而右侧不加限制，进而实现筛面沿z向移动，从而实现3个移动2个转动的运动形式[19]。

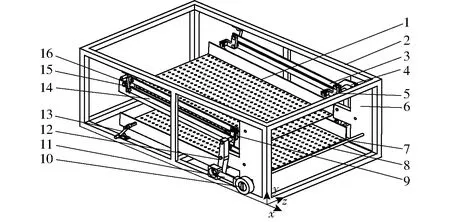
图3 三移动两转动振动筛模型Fig.3 Model of vibrating screen with three translations and two rotations1.上筛 2.机架 3.导杆A 4.限位杆 5.V型杆 6.侧板 7.下筛 8.主轴 9.T型杆 10.偏心轮 11.连杆 12.摇杆 13.支撑杆 14.导杆B 15.吊杆 16.球铰

2 颗粒非线性跳动理论分析

以平面往复、三移动一摆动、三移动两转动振动筛与试验台架为研究对象，根据振动筛的物理样机，推导筛面运动方程，把筛面等距划分成若干条直线，如图4所示。建立玉米颗粒与筛面上每条直线的碰撞示意图，如图5所示。

图4 筛面直线分布Fig.4 Lines distribution on screen

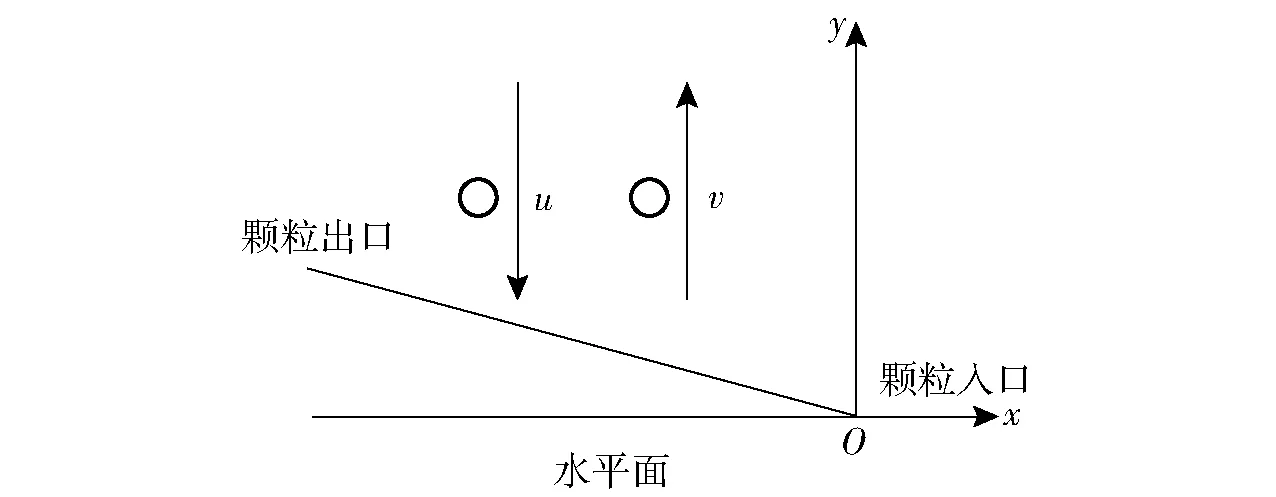
图5 颗粒与筛面碰撞示意图Fig.5 Collision diagram between grain and screen

图5中以筛面上任意一点λ为坐标原点建立直角坐标系，空心圆表示颗粒在xOy面的投影，u、v分别表示颗粒趋向和离开筛面时y向的速度，O点y向的速度为vyo，若tj时刻粒子与筛面发生第j次碰撞，根据弹性碰撞规律有[9,13]

v(tj)-vyo(tj)=-δ(u(tj)-vyo(tj))

(1)

式中δ——速度恢复系数，一般取0.5[13]

颗粒第j次离开筛面的速度近似等于第j+1次趋向筛面速度，即

u(tj+1)=-v(tj)

(2)

将式(2)代入式(1)整理可得

v(tj+1)=δv(tj)+(1+δ)vyo(tj+1)

(3)

由于颗粒与筛面碰撞时间极短，相对于颗粒上抛与下落的时间可忽略，则

(4)

将式(3)两边乘以2ω1/g，式(4)两边乘以ω1。ω1为振动筛结构中曲柄的角速度。

在3种振动筛中分别有[7，19]

vyo1=l81ω51cosθ51+l31ω31cosθ31

(5)

vyo2=ω12l12cosθ12+ω22l22sinθ22+ω32lM2cosθ32

(6)

(7)

(8)

(9)

其中ω51=f11(ω1t)θ51=f31(ω1t)

ω31=f21(ω1t)θ31=f41(ω1t)ω12=f12(ω1t)θ12=f22(ω1t)ω22=f32(ω1t)θ22=f42(ω1t)ω32=f52(ω1t)θ32=f62(ω1t)ω33=f13(ω1t)θ33=f23(ω1t)ω53=f33(ω1t)θ53=f43(ω1t)ωβ3=f53(ω1t)θβ3=f63(ω1t)ω73=f73(ω1t)θ73=f83(ω1t)

式中vyo1、vyo2、vyo3——平面往复、三移动一摆动、三移动两转动振动筛筛上O点y向的速度，m/s

li1、li2、li3——平面往复、三移动一摆动、三移动两转动振动筛中第i个杆件的长度，mm

θi1、θi2、θi3——平面往复、三移动一摆动、三移动两转动振动筛中第i个杆件与x轴的方位夹角，rad

ωi1、ωi2、ωi3——平面往复、三移动一摆动、三移动两转动振动筛中第i个杆件的角速度，rad/s

θβ3——筛面在yOz平面内的倾角，rad

ωβ3——筛面在yOz平面内的角速度，rad/s

lN3——筛面上任意一点N与筛面左侧的距离，mm

lM2、lM3——三移动一摆动、三移动两转动振动筛筛面上任意一点M与筛面前端的距离，mm

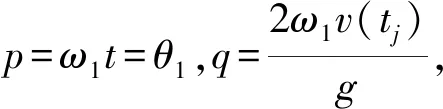
(10)

(11)

在3种振动筛中有[7，19]

f1(pj+qj)=l81f11(pj+qj)cos(f31(pj+qj))+l31f21(pj+qj)cos(f41(pj+qj))

(12)

f2(pj+qj)=l12f12(pj+qj)cos(f22(pj+qj))+l22f32(pj+qj)· cos(f42(pj+qj))+lM2f52(pj+qj)cos(f62(pj+qj))

(13)

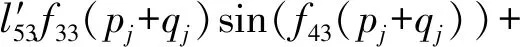
(14)

式中f1(pj+pq)——平面往复振动筛二维映射中的函数

f2(pj+pq)——三移动一摆动振动筛二维映射中的函数

f3(pj+pq)——三移动两转动振动筛二维映射中的函数

fi1(pj+pq)——平面往复振动筛二维映射中的变量

fi2(pj+pq)——三移动一摆动振动筛二维映射中的变量

fi3(pj+pq)——三移动两转动振动筛二维映射中的变量

式(10)若存在一系列不动点K，那么qj=0，由于A≠0，所以f(pj+qj)=0。对f(pj+qj)=0进行数值计算，获得解沿筛面长度L的分布情况如图6所示。表明在一个周期内f(pj+qj)=0方程均有解，可知式(10)存在一系列不动点K。

图6 不同驱动机构f(pj+qj)的零点分布Fig.6 Zero distribution of f(pj+qj) of different driving mechanisms

式(10)的雅可比矩阵为

(15)

其特征值方程

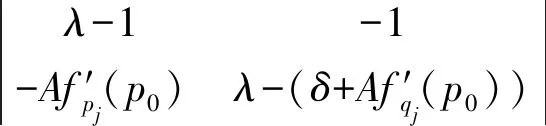
(16)

其特征值为

(17)

(18)

特征值λ通过Matlab数值模拟得出，对于平面往复、三平移一摆动、三平移两转动3种筛分模式，利用公式(17)、(18)计算λ时所用的初始值均为：δ=0.5，A=2ω1(δ+1)/g，ω1=2πn，n=240 r/min。

颗粒在筛面上跳动的周期稳定性与不动点K的稳定性等价，不动点K的稳定性由二维映射的雅可比矩阵的特征值λ1、λ2共同决定，由混沌运动理论可知[20]：若0<λ1<1，0<λ2<1，不动点K为稳定结点；若λ1>1，λ2>1，不动点K为不稳定结点；若0<λ1<1，λ2>1(或0<λ2<1，λ1>1)，不动点K为鞍点；若λ1与λ2为共轭复数且|λ1|=|λ2|<1，不动点K为稳定焦点；若λ1与λ2为共轭复数,且|λ1|=|λ2|>1，不动点K为不稳定焦点；若特征值|λ1|<1，|λ2|<1，则不动点K稳定，颗粒具有稳定的周期运动；否则颗粒将发生分岔，可能走向混沌。

基于Matlab数值计算及可视化功能对3种振动筛的不动点映射特征值进行数值模拟。在筛面长度范围内，特征值的数值模拟结果如图7所示。

图7 特征值变化曲线Fig.7 Changing curves of characteristic value

由图7a可知，颗粒在平面往复振动筛不同的筛长范围内会产生不同的运动形式。在筛面长度0～322 mm内，|λ1|>1，|λ2|>1，不动点为不稳定结点，颗粒发生混沌运动；在筛面长度322～397 mm内，|λ1|>1，0<|λ2|<1，不动点为鞍点，受到轻微干扰后，不动点失稳，颗粒将发生倍周期分岔运动；在筛面长度397～461 mm内，|λ1|、|λ2|均小于1，不动点为稳定结点，颗粒发生稳定的周期运动；在筛面长度461～780 mm内，|λ1|、|λ2|均大于1且为共轭复数，不动点为不稳定焦点，不动点失稳，颗粒将发生Hopf分岔运动；在筛面长度780～1 360 mm，|λ1|>1，|λ2|>1，不动点为不稳定结点，不动点失稳，颗粒发生混沌运动[7,21]。

由图7b、7c可知，沿筛面长度方向，三移动一摆振动筛和三移动两转动振动筛的特征值始终满足|λ1|>1，|λ2|>1，两直线未出现交叉点,并且两个特征值的绝对值相差很大，由此可推断在三移动一摆振动筛和三移动两转动振动筛的筛面上，不动点为不稳定结点，不动点失稳，颗粒均发生混沌运动。

3 平板上颗粒群分散性试验

3.1 试验材料与装置

选取德美亚一号玉米作为研究颗粒群分散性的试验材料。玉米颗粒形状包括球形、锥形、矩形，各自所占的百分比分别为15.8%、74.1%、10.1%[22]，如图8所示。每次试验选用同一组颗粒。

图8 试验材料Fig.8 Experimental material1.锥形玉米 2.矩形玉米 3.球形玉米

为了对比玉米颗粒群在不同振动筛筛面上的分散程度，试验装置主要由平面往复振动筛、三移动一摆动振动筛、三移动两转动振动筛、高速摄像机(Phantom V5.1)、新闻灯、变频器(MM430 6ES6430-2UD27-56CA0)和电动机(Y2-132M2-6)等组成，如图9所示。

3.2 试验内容与方法

高速摄像机可获取筛面运动信息，为了定量分析颗粒群在筛面上运动特性，需要利用标尺标定比例尺寸。试验时在筛面上粘贴白色0.04 m长纸条作为标尺[7]。

图9 试验装置Fig.9 Experimental devices1.高速摄像机 2.振动筛 3.变频器 4.电动机 5.抖动板

为了分析颗粒的运动规律，获得玉米颗粒群在3种振动筛筛面上的分散情况，进行颗粒群分散性平板试验。试验前在Phantom软件中将高速摄像机拍摄速率设定为300帧/s。选取40颗玉米颗粒，将变频器调节到试验所需频率后，启动电机，通过变频器转换电机转速，利用高速摄像机拍摄试验装置主轴不同转速下颗粒群的分散情况。利用高速摄像后处理软件Phantom建立绝对坐标系，创建坐标原点，选取筛面上具有代表性的玉米颗粒作为追踪对象，由人眼逐帧进行跟踪，提取帧数间隔为15帧，利用软件读取单颗粒在不同时刻的坐标。

3.3 试验指标

以分散度为试验指标，以主轴转速为试验因素。采用Txz评价颗粒群沿筛面长度和宽度方向的分散情况[17]。

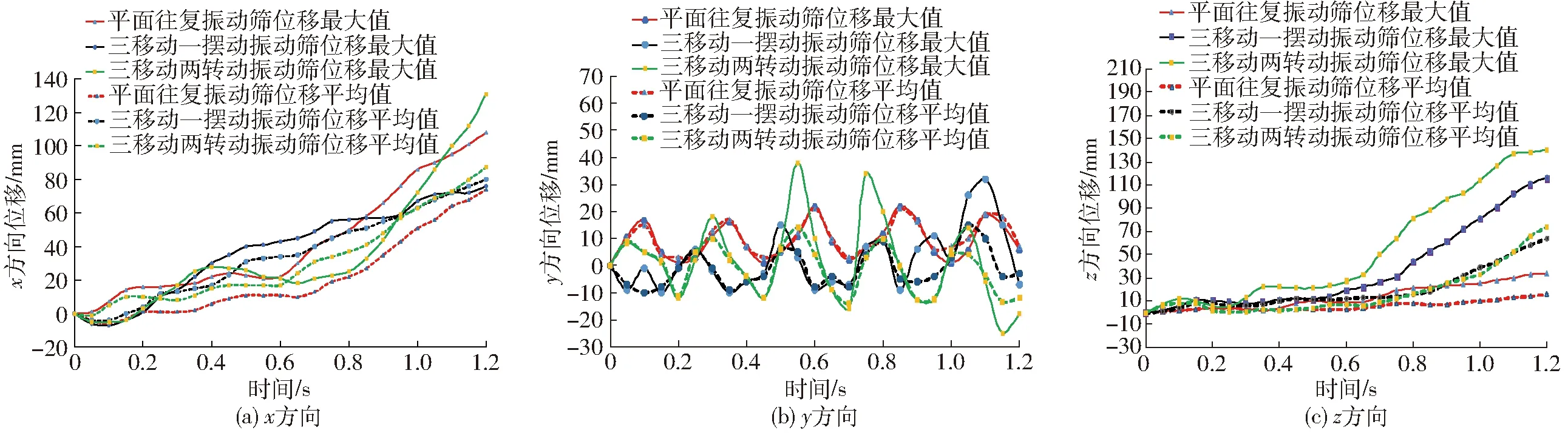
图10 3种振动平板上颗粒位移对比Fig.10 Comparison of particle displacement on three types of vibrating plate

(19)

(20)

因为标准偏差可以反映样本颗粒在集聚中心的离散程度，标准偏差越大，表明颗粒群的分散程度越好，因此，采用样本坐标的标准偏差来衡量不同振动平板上颗粒群的分散程度，则t时刻颗粒群沿筛面x、z方向样本标准差计算式为[17]

(21)

(22)

将物料颗粒运动的时间分为m个时间段，得到基于平板上颗粒沿x、z方向综合分散度评价指标为[17]

(23)

3.4 试验结果与分析

3.4.1颗粒运动位移

将颗粒在不同时刻x、y、z方向的坐标分别连接，获得颗粒在不同方向的运动轨迹，如图10所示。

由图10a可知，随着时间的增加，颗粒沿3种振动平板x方向的位移整体上呈现逐渐增大的趋势。在0.6 s，颗粒群沿三移动一摆动振动平板x方向的位移最大，其次为三移动两转动振动平板、平面往复振动平板。表明在0～0.6 s内，三移动一摆动振动平板的运动形式更利于颗粒群沿平板x方向快速分散；在1.2 s，由颗粒位移的平均值可知，颗粒群在三移动两转动振动平板上的位移和三移动一摆动振动平板上的位移大于在平面往复振动平板上的位移，表明三移动一摆动和三移动两转动振动平板较平面往复振动平板更利于颗粒沿x方向的快速分散。这是由于三移动一摆动和三移动两转动振动平板沿z方向的转动加速了平板对颗粒群沿x方向的推送能力。

由图10b可知，在平面往复振动平板中，颗粒位移沿平板y方向呈周期性变化，这与颗粒非线性理论分析的结果一致；颗粒沿三移动两转动振动平板和三移动一摆动振动平板y方向的最大位移分别为38 mm和32 mm，体现了这两种振动平板的最大抛送能力。颗粒沿y方向的位移变化较复杂，呈现混乱的运动趋势。这是因为随着时间的增加，三移动一摆动和三移动两转动振动平板具有多维运动，颗粒在每次跃起后再次与平板接触的位置具有随机性。当颗粒再次与平板接触时，颗粒在平板上可能发生上移、下移或伴随着平板摆动产生侧滑，故颗粒在两种振动平板上产生混沌运动，这与颗粒非线性跳动理论分析的混沌运动结果一致。由于混沌运动的随机性，增加了物料与筛面的碰撞机会，从而提高颗粒群在三移动一摆动和三移动两转动振动筛筛面上的透筛几率。

在图10c中，由颗粒位移最大值和平均值可知，颗粒群在三移动两转动振动平板z方向的位移明显大于另外两种振动平板。这是由于三移动两转动振动平板较另外两种振动平板产生沿x方向的转动，该转动会使颗粒每次与平板接触时产生不同方向的碰撞，利于颗粒沿z方向向平板两端分散。

综上分析图10a、10c可得，颗粒在振动平板x与z方向的位移随着时间的变化呈现逐渐增大的趋势，说明颗粒群在平板x、z方向分散性逐渐增大，利于颗粒沿平板x、z方向的分散，有效增加了平板的利用面积。

3.4.2颗粒运动速度

根据位移与时间之比获得速度，将颗粒不同时刻的速度依次连接，获得颗粒速度曲线，如图11所示。

图11 3种振动平板上颗粒速度变化曲线Fig.11 Velocities curves of particle on three types of vibrating plate

由图11a可知，在平面往复振动平板上，颗粒沿x方向的速度呈周期性变化，在运动0.1 s之后，速度值始终为正值，表明颗粒沿平板呈一直往筛后运动的状态；在三移动一摆动振动平板和三移动两转动振动平板上颗粒运动混乱，速度变化范围分别为-0.56～2.21 m/s、-0.60～2.10 m/s。说明颗粒在筛面上做前后往复式运动，该运动形式增加了颗粒与筛面的碰撞时间，利于颗粒透筛。1.2 s时，颗粒沿筛面x方向，在三移动一摆动振动筛上的速度大于三移动两转动振动筛上的速度和平面往复振动筛上的速度。

由图11b可知，颗粒在平面往复、三移动一摆动、三移动两转动振动平板上，沿y方向的速度变化范围分别为-2.10～1.88 m/s、-1.01～1.40 m/s、-2.60～3.36 m/s。1.2 s时，颗粒沿筛面y方向，颗粒在三移动两转动振筛上的速度与平面往复振动筛上的速度相近，均大于三移动一摆动振动筛上的速度。

由图11c可知，颗粒在三移动两转动振动平板上，沿z方向的速度变化范围最大，其速度变化范围为-0.80～1.96 m/s，利于颗粒沿平板z方向快速分散。而在平面往复和三移动一摆动振动平板上速度变化范围很小，其速度变化范围分别为-0.20～0.46 m/s、-0.16～0.92 m/s，这是由于三移动两转动振动筛产生的沿平板x方向的转动较三移动一提动振动筛产生的沿x方向的移动效果更佳。1.2 s时，颗粒沿筛面z方向，在三移动两转动振动筛上的速度大于三移动一摆动振动筛和平面往复振动筛上的速度。

3.4.3不同转速下颗粒群的分散度

根据颗粒不同时刻的坐标，以及分散性指标计算公式获得3种振动筛不同主轴转速下颗粒群的分散度，确定3种振动平板上颗粒群最佳分散度对应的主轴转速，如图12所示。

图12 分散度随主轴转速的变化Fig.12 Variation of dispersion with spindle speed

图13 颗粒群在振动平板x、z方向上分散度变化过程Fig.13 Variation process of dispersivity of particle group in x，z direction on vibrating plate

由图12可知，随着主轴转速逐渐增大，颗粒群在3种振动平板上的分散度都呈现先增大后减小的变化规律。在平面往复振动平板上,随着主轴转速逐渐增大，颗粒群的分散度具有较显著的变化。当主轴转速为240 r/min时，颗粒群的分散度Txz达到最大，表明颗粒群在平面往复振动平板上最优分散度对应的最佳主轴转速为240 r/min；在三移动一摆动振动平板和三移动两转动振动平板上，当主轴转速由210 r/min增大至270 r/min时，颗粒群的分散度变化幅度明显，颗粒群最优分散度对应的最佳主轴转速分别为250 r/min和240 r/min。

3.4.4主轴最优转速下颗粒群的分散度

在3种振动筛主轴最优转速下，跟踪不同时刻颗粒群的分散情况，如图13所示。

综上分析，筛分时间为1.2 s时，三移动两转动振动平板上颗粒群的综合分散效果优于三移动一摆动振动平板，和平面往复振动平板。说明三移动一摆动和三移动两转动实现的多维运动形式较平面往复振动实现的平面运动形式更利于加速颗粒群在振动平板上的分散。

表1 颗粒群分散度对比Tab.1 Dispersion comparison of particle groups mm

由表1可知，在相同试验工况下，颗粒群在平面往复振动平板上的综合分散度为34.06 mm，颗粒群在三移动一摆动和三移动两转动振动平板上的综合分散度分别为38.96 mm和40.73 mm，较平面往复振动平板综合分散度分别提高14.39%和19.58%，有效提高了颗粒群物料在筛面上的分散程度，减少了颗粒群在筛面上的堆积，增加了筛面的实际筛分面积，提高了筛分效率。同时，三移动两转动较三移动一摆动多1个沿x方向的转动，综合分散度提高了4.54%。说明沿x方向的转动对颗粒群的分散效果具有显著作用。

4 物料筛分试验

为验证分散性平板试验的可行性及试验结果的正确性，用振动筛筛面代替振动平板，进行物料筛分验证试验，清选装置筛面采用圆孔筛(筛孔直径、纵向间距和横向间距分别为15、30、17.5 mm),筛面长度为1 360 mm，宽度为1 100 mm，筛体厚度为2 mm，筛面振动频率为4 Hz，筛面振幅为19.5 mm，筛面安装倾角为3.5°，在清选装置前端安装抖动板喂入谷物，安装夹角为1.74°，抖动板尾部与筛面垂直距离约75 mm，根据《农业机械设计手册》要求，抖动板尾部高于筛面最大距离为100 mm。试验连续5 s喂入25 kg玉米脱出物，将玉米脱出物按比例(玉米籽粒占73.3%、玉米茎秆占17.6%、玉米芯占8.7%、轻质杂余占0.4%[19])称量后均铺在抖动板上，以保证喂入量为5 kg/s，如图9所示。以分散度和筛分效率作为试验指标，对玉米脱出物在3种振动筛筛面上进行分散性高速摄像台架试验，实时追踪玉米颗粒群的分散情况，结果如图14所示。通过提取试验数据，获得分散度、筛分效率与时间之间的关系，如图15所示。

随着筛分时间的增加，玉米脱出物在平面往复振动筛筛面上呈现向筛面一侧局部堆积的状态，如图14a所示。这一结果与平板试验结果相一致，说明简单的往复运动形式不利于颗粒在筛面上快速透筛；在筛分2.4 s时，三移动一摆动振动筛的筛分效果优于平面往复振动筛的筛分效果，如图14b所示。这是由于三移动一摆动振动筛较平面往复振动筛产生了沿筛面z方向的移动与摆动，更利于颗粒与筛面的接触，增加了颗粒的透筛几率；在三移动两转动振动筛筛面上，玉米脱出物的分散度最好，相同时刻，透筛效率最高。

在筛分2.4 s时，颗粒留在三移动两转动振动筛筛面上的数目少于三移动一摆动振动筛筛面上的数目，并少于平面往复振动筛筛面上的数目。这是由于颗粒群在筛面上的分散度越好，颗粒群与筛面的接触几率越多，颗粒透筛机会就越大。

图14 颗粒群在3种振动筛筛面上的分散度Fig.14 Dispersion of particles in three kinds of vibrating screen

图15 筛分效率、分散度与时间的关系曲线Fig.15 Relationship curves between screening efficiency and dispersion and time

由图15可知，随着筛分时间增加，筛分效率与分散度都逐渐增大，说明颗粒群的分散度与筛分效率呈同步变化趋势，物料筛分试验证明了分散度越大，筛分效率越高。由图15可得，在0.2～0.4 s和0.6～0.8 s时间内，三移动两转动振动筛筛分效率变化很大，说明在这段时间内颗粒群的分散度很大，颗粒大量透筛。而在0.8～1.2 s时，三移动两转动振动筛的分散度逐渐增大，但筛分效率逐渐趋于平缓，颗粒群接近完全透筛。

由图14和图15分析可知，3种振动筛的筛分效率由高到低依次为：三移动两转动振动筛、三移动一摆动振动筛、平面往复振动筛。物料筛分试验结果与平板试验结果相一致。筛分试验证明了用平板对颗粒群分散度进行研究的可行性，同时也验证了平板试验结果的正确性。