剪刀式桥梁展桥机构铰点位置多目标优化设计
2019-06-27韩军朱鹏程张帅洪煌杰
韩军, 朱鹏程, 张帅, 洪煌杰
(1.陆军研究院 5所,江苏 无锡 214035; 2.陆军工程大学 野战工程学院, 江苏 南京 210007)
0 引言
剪刀式架设是军用桥梁的一种典型架设方式,已在国内外军用桥梁中得到广泛应用。剪刀式架设的军用桥梁有美军JAB联合冲击桥、波兰S-20冲击桥[1]、英军BR90桥梁族的近距离支援桥,以及我军某型轮式冲击桥、重型机械化桥[2]等。传统的展桥机构采用双油缸驱动、单油缸驱动链条展桥或钢丝绳驱动翻转架展桥,三者的共同特点是运输状态展桥机构突出桥节以外,增加了运输长度,不利于装备机动。英军BR90近距离支援桥采用液压机构实现桥梁的展开和撤收,实现了自动展桥功能[3]。
在展桥机构研究方面,为提高桥梁架设作业的平顺性、架设速度和安全性,文献[4]研究了军用折叠桥梁机构架设轨迹优化及其自动控制问题。文献[5]提出了一种新型救灾用可展拱桥体系,包括可展桥体系、构件、连接、展开方式等;通过建立模型验证了展桥的承载能力和结构性能,该展桥具有构件轻巧、运输方便、施工快捷、承载力大等优点。文献[6-7]介绍了一种新型剪刀式抢险机动桥,该桥采用剪刀式展开机构,在5~10 min内可架设20.8 m长的桥梁结构,桥体质量约为13 t,可以在受自然灾害破坏的地方快速构筑桥梁通道,并通过试验研究了该桥梁在自由和强迫载荷条件下的应变和动态特性。文献[8]研究了剪刀式桥折叠和展开过程中的几何特性、运动特性和结构响应问题,采用灵敏度分析方法评估分析了设计参数对剪刀桥的结构应力、变形和质量参数的影响。文献[9]研究了一种基于铝合金桁桥架的模块化拱桥结构。文献[10]研究了一种采用剪式铰和套筒可展机构实现轴向展开的轻型展桥机构。
展桥机构是实现剪刀式桥梁架设的关键部件,由于展桥机构要求内置于桥节中,无论桥梁在折叠状态还是在展开状态下,均要求展桥机构不露出桥面,因此其外形结构要求紧凑,同时展桥机构采用油缸驱动,驱动油缸既要满足折叠和展桥状态要求即实现180°回转,又要满足一定的驱动力臂要求。另外,展桥机构是一个较复杂的单自由度多连杆机构,展桥过程是一种机构复合运动,机构的受力状态复杂。在展桥机构中,其铰点位置涉及展桥机构功能实现、驱动油缸选取及桥梁结构强度设计等因素,设计时仅凭经验和机构仿真分析软件,难以实现展桥机构铰点位置的最优设计。
新型展桥机构在某型剪刀式桥梁上得到了应用,在方案样机试验过程中发现在桥梁架设的初始状态,出现展桥机构驱动油缸的小腔由于压力过大引起间断液压油溢流现象,为此需要开展展桥机构的优化设计工作。
本文介绍一种新型内置式军用剪刀桥梁展桥机构[11],其工作原理为,采用一个液压油缸驱动转架机构,实现桥节的折叠与展开,该机构具有结构简单、紧凑,方便部队机动等优点。利用Denavit-Hatenberg齐次变换矩阵[12]建立了展桥机构的运动学、静力学和关键铰点的多目标优化模型;结合工程实例对剪刀式桥梁展桥机构的关键铰点进行了优化设计,并用ADAMS软件对优化计算模型进行了验证。
1 剪刀式桥梁工作原理与建模
1.1 工作原理
剪刀式桥梁由2个桥节组成,双剪刀式桥梁由3个桥节组成,每两个桥节通过展桥机构驱动,采用剪刀式作业原理,即架设时先展开我岸两个桥节、再展开对岸桥节,从而形成两次剪刀式展桥过程、完成架设作业。双剪刀式桥梁展桥主要步骤(见图1)如下:
步骤1运载车辆达到架桥点后,翻转架油缸、顶起翻转架,使桥跨置于垂直状态;伸出支腿油缸,使础板着地(见图1(a))。
步骤2通过驱动舌形臂油缸和展桥油缸调整桥节角度,依次展开各桥节,直至桥跨完全展开(见图1(b)、图1(c))。
步骤3继续伸舌形臂油缸,使舌形臂向右旋转,直至桥跨端部与对岸着地(见图1(d))。
1.2 展桥机构运动学建模
图2所示为剪刀式桥梁结构示意图,主要由翻转架、第1桥节、第2桥节(含第3桥节)和展桥机构组成。图中A、B、C、D、E、F、O、O1、O2、O3表示铰点,翻转架通过铰点O1与第1桥节连接,由舌形臂油缸AB驱动第1桥节运动;第1、2桥节通过铰点O2连接,其内部安装有展桥机构,可以实现两个桥节的运动。展桥机构由转架O3EF、连杆EC和展桥油缸FD组成,其中转架O3EF通过铰点O3与第2桥节连接,通过连杆EC与第1桥节连接,展桥油缸FD的D点位于第2桥节上。工作时,展桥油缸驱动转架旋转,通过连杆带动第1桥节旋转(实际是第1桥节静止、第2桥节运动)。展桥机构需要实现第1桥节与第2桥节的折叠和展开功能,且展桥机构需要在运输和展开状态下内置于桥体中,便于桥梁的运输和工作。
下面建立展桥机构的运动学模型。以翻转架与副车架的连接铰点O为坐标原点,建立基{w}坐标系Oxy,在该坐标系中A点为翻转架上舌形臂油缸支座;以第1桥节与翻转架铰接点O1为坐标原点,建立基{w1}坐标系O1x1y1,其中规定当第1桥节垂直地面时为初始状态,此时y1轴方向竖直向上,在该坐标系中,B点为舌形臂油缸的另一端支座,C点为连杆EC铰接点;以第1桥节与第2桥节铰点O2为坐标原点,建立基{w2}坐标系O2x2y2,其中规定x2轴方向在初始状态时与x1轴方向一致,在该坐标系中,D点为展桥油缸铰点;以第2桥节与展桥机构铰点O3为坐标原点,建立基{w3}坐标系O3x3y3,其中规定x3方向与转架O3E方向一致,在该坐标系中,铰点E为展桥机构与连杆的连接点,铰接点F为展桥机构与展桥油缸的连接点。点G1、G2、G3和G4分别为第1桥节、第2桥节、展桥机构和展桥油缸的质心。各个坐标轴方向如图2所示。
设θ1为{w1}坐标系相对于{w}坐标系的旋转角度,wO1x、wO1y为O1点在{w}坐标系下的坐标;θ2为{w2}坐标系相对于{w1}坐标系的旋转角度,w1O2x、w1O2y为O2点在{w1}坐标系下的坐标;θ3为{w3}坐标系相对于{w2}坐标系的旋转角度,w2O3x、w2O3y为O3点在{w2}坐标系下的坐标。利用Denavit和Hartenberg齐次变换[12],可建立两节剪刀式桥梁的各个机构之间的姿态转换矩阵为
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
采用类似方法,可得到其他铰点和重心在坐标系{w}的坐标向量,从而可进一步确定剪刀式桥梁展桥过程中任意姿态下桥节与展桥机构各个铰点的运动坐标、相互位置关系;相应地,可得到剪刀式桥梁的运动学模型。
1.3 展桥机构静力学模型
由于架桥过程中的速度较低,在展桥过程某一状态下,桥梁机构中的受力按静力学模型处理。下面利用展桥机构的力和力矩平衡条件,对其进行求解。
由图2,以桥整体结构为研究对象,由铰点O1所受力矩平衡得∑MO1=0,有
f1·dO1AB-m1g(xm1-xO1)-m2g(xm2-xO1)-
m3g(xm3-xO1)-m4g(xm4-xO1)=0,
(10)
式中:f1为舌形臂油缸驱动力;dO1AB为力臂,表示铰点O1到AB的距离;m1、m2、m3和m4分别为第1桥节、第2桥节(含第3桥节)、转架和展桥油缸的质量;xm1、xm2、xm3、xm4分别为其质心在{w}坐标系下的x轴坐标;xO1为铰点O1在{w}坐标系下的x轴坐标。
由水平方向的受力平衡得∑X=0,有
fO1x-f1cosα1=0,
(11)
式中:fO1x为支座铰点O1所受到的水平分力;α1为舌形臂油缸的水平夹角。
由竖直方向的受力平衡得∑Y=0,有
fO1y-f1sinα1-(m1+m2+m3+m4)g=0,
(12)
式中:fO1y为支座铰点O1所受到的垂直分力。
图3中fO2x、fO2y分别表示铰点O2所受到的水平分力和垂直分力。图4中fO3x、fO3y分别表示铰点O3所受到的水平分力和垂直分力。
以第1桥节为研究对象(见图3),由铰点O2所受力矩平衡得∑MO2=0,有
-fO1y(xO2-xO1)+fO1x(yO2-yO1)-
f1dO2AB+m1g(xO2-xm1)-fEC·dO2EC=0,
(13)
式中:[xO2,yO2]、[xO1,yO1]分别为铰点O2、O1在{w}坐标系下的坐标;dO2AB为力臂,表示铰点O2到AB的距离;dO2EC为力臂,表示铰点O2到EC的距离。
以转架为研究对象(见图4),由铰点O3所受力矩平衡得∑MO3=0,有
-f2·dO3FD+m3g(xO3-xm3)+
fEC·dO3EC=0,
(14)
式中:f2为展桥油缸驱动力;dO3FD为力臂,表示铰点O3到FD的距离;xO3为铰点O3在{w}坐标系下的x轴坐标;dO3EC为力臂,表示铰点O3到EC的距离。
综上所述,利用(1)式~(14)式就可以计算得到任意姿态下,舌形臂油缸、展桥油缸的驱动力臂dO1AB、dO3FD及其驱动力f1和f2.
2 展桥机构及其驱动油缸铰点优化分析
在剪刀式桥梁中,展桥机构转架O3EF的形状、连杆CE中E铰点的位置和展桥驱动油缸FD中D铰点的位置,对展桥机构的功能实现及其展桥驱动油缸的受力状态起着决定性影响。下面对其影响因素和制约条件进行分析。
首先,展桥机构需要满足第1桥节和第2桥节展开成一字形和折叠的要求,实现架桥和折叠运输的功能。其次,转架O3EF在剪刀式桥梁展开和折叠状态下满足不露出桥面条件。再次,展桥驱动油缸应满足最大伸长长度和最小安装尺寸比例范围要求。最后,各种展桥姿态下,展桥驱动油缸的最大驱动力(或压力)最小化,以满足展桥驱动机构的小型化和降低液压系统工作压力的要求。
为此,对连杆铰点C、驱动油缸的铰点D和展桥转架O3EF各铰点的位置进行优化设计。设各个铰点的坐标为优化设计变量,分别为C(x1,y1)、D(x2,y2)、E(x3,y3)、F(x4,y4),其中铰点C为基{w1}下的坐标,铰点D为基{w2}下的坐标,铰点E和F为基{w3}下的坐标。
为了得到优化变量值,分两步进行求解。
1) 已知第2桥节转角θ2,求解转架的旋转角度θ3.
由于展桥机构为一个单自由度系统,根据展桥机构的运动学模型,以第2桥节转角θ2为中间变量,利用转桥机构中连杆CE在任意状态下长度相等的约束条件,即
LCE(x1,y2,…,x4,y4)-
SCE(x1,y1,…,x4,y4,θ2,θ3)=0,
(15)
式中:LEC(x1,y1,…,x4,y4)为θ2=0和θ3=0条件下连杆CE的初始长度;SCE(x1,y1,…,x4,y4,θ2,θ3)为转桥机构不同位置时连杆CE的长度。(15)式为
一个非线性方程,给定θ2值后,可利用优化算法求解该方程得到θ3值。
2) 利用多目标优化模型,对优化变量进行求解。
优化目标是:第1桥节在倾角θ1=-40°(经验值,通常θ1∈[-43°,-35°])时,第2桥节转角θ2∈[0°,180°]范围内,展桥驱动油缸的驱动力f2(1)和闭锁力f2(2)最大值最小化,并满足展桥机构液压驱动油缸的选型条件,即
minf(x1,y1,…,x4,y4)=
c(1)|f2(1)|+c(2)|f2(2)|,
(16)
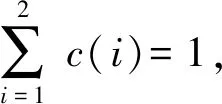
约束条件是:展桥驱动油缸的工作行程满足最大行程和最小行程的比例范围要求;三角转架O3EF不翻转及满足三角形的边长条件;展桥机构折叠和展开时,关键铰点不露出桥面等;铰点在空间布置上,满足最低的安装和布置条件等。
针对上述选取的优化变量,确定的约束条件以及优化目标,采用信赖域法[13]对(16)式优化模型进行求解。
3 方案样机优化计算及验证分析
3.1 方案样机优化
某方案样机已知优化变量值(经验值)如表1所示。

表1 某方案样机已知变量值
另外,已知第1桥节质量为500 kg,第2、3桥节质量为1 360 kg,转架质量为35 kg,展桥油缸质量为45 kg,质心位置如图1所示。
利用展桥机构的多目标优化计算模型,以θ1=-40°最常用的状态为优化工况,依据展桥驱动油缸初步选型情况(最大闭锁压力为17 t,最大推力为26 t),确定多目标的权重系数为0.395 3和0.604 9,可得到变量的优化值如表2所示。

表2 某方案样机优化后变量值
将展桥机构优化后变量值代入力学计算模型,θ1分别取-35°、-40°和-43°,θ2的变化范围为[0°,180°],可得到优化前和优化后展桥机构驱动油缸推力f2的对比情况,分别如图5~图7所示。
由图5可以看出,总体上,随着第2桥节的展开,展桥油缸压力变化由受拉状态变化为0,然后逐渐变为受压状态,展桥油缸受力与实际的状况吻合。优化前,θ2=0°时f2对应的最大拉力值-2.494 3×105N,θ2=75.6°时f2对应的最大推力值1.915 0×105N,液压油缸的理想受力情况下,最大推力值(大腔作用)应大于最大拉力值(小腔作用),而此时实际受力却相反。同时也可从图6、图7看出,展桥机构驱动油缸的实际最大拉力值均大于最大推力值,展桥油缸受力状态不合理,表明展桥机构铰点设计不科学。
优化前模型所反映出的θ2=0°时展桥油缸所受拉力过大的问题,与方案样机试验过程中,在桥梁架设的初始状态,展桥机构驱动油缸的小腔由于压力过大引起间断液压油溢流现象相吻合,特别是在初始状态θ2=0°时,θ1值越小(-43°),液压油缸所受拉力f2越大,过载情况越严重。
根据图5~图7的经验值和优化后曲线数据,可得到展桥油缸最大拉力和最大推力值的情况比较如表3所示。
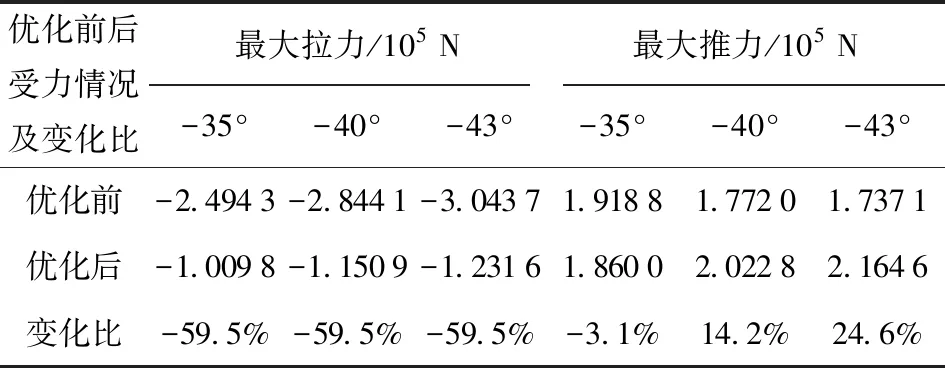
表3 优化前后展桥油缸受力情况比较
从表3中可以看出,优化后展桥油缸的最大受力状态均有明显改善,如在θ1=-35°时,最大拉力由-2.494 3×105N减小到-1.009 8×105N,降低59.5%,最大推力由1.918 8×105N减小到1.860 0×105N. 整体上,优化后展桥油缸的最大推力与最大拉力(闭锁力)得到了明显改善,如θ1=-35°时,最大推力约为最大拉力1.84倍的关系,与多目标优化的权重值基本一致,表明展桥油缸的受力合理,便于展桥油缸的选型,展桥机构铰点优化值满足设计要求。另外,不同于优化前,优化后θ1越大(-35°),展桥驱动油缸受力状况越好;θ1越小(-43°),展桥驱动油缸受力状况越差,与实际展桥油缸的受力状态相一致。
铰点优化后,展桥时四连杆机构CEO2O3中连杆O2O3转角β、第2桥节转角θ2和转架O3EF转角θ3的变化情况如图8所示。从图8中可以看出,第2桥节转动180°时,β的变化范围为[-90.229 5°,89.775 0°],θ3的变化范围为[-22.654 2°,80.961 9°],转架呈顺时针转动,变化曲线均略呈线性变化,机构转动状态连续平稳。
3.2 ADAMS验证分析
利用机械系统动力学分析ADAMS软件[14-15]建立剪刀桥的运动学模型,分别将优化前和优化后机械系统动力学分析变量作为输入值,依据剪刀桥的结构参数,得到展桥机构的模型如9所示。
当θ1=-40°、θ2的变化范围为[0°,180°]时,分别得到优化前和优化后,展桥油缸推力随着第2桥节转角θ2的变化曲线分别如图10、图11所示。
由图10可以看到,当θ2=0°时展桥油缸受到的最大拉力为-2.837 6×105N,当θ2=86.1°时油缸的最大推力为1.776 4×105N,与本文的计算最大拉力-2.844 1×105N和最大推力1.772 0×105N值基本相同。由图11可以看出,当θ2=0°时展桥油缸受到的最大拉力为-1.145 9×105N,当θ2=179.3°时油缸的最大推力为2.024 1×105N,与本文的计算最大拉力-1.150 9×105N和最大推力2.022 8×105N值基本相同。以上结果表明,本文的优化计算模型与ADAMS模型一致,优化模型正确。
4 结论
本文阐述了一种新型剪刀式桥梁展桥机构的工作原理,通过理论建模、工程样机优化计算和验证分析,得到以下主要结论:
1) 根据展桥油缸的闭锁力和推力不同的特点,提出了满足展桥油缸选型的展桥机构铰点设计多目标优化计算方法,该方法有效可行。
2) 优化后,方案样机展桥油缸的最大拉力降低幅度达59.5%,解决了方案样机架桥初始状态展桥油缸由于压力过大出现间断溢流问题。同时,展桥油缸的最大推力和最大拉力分布趋于合理,展桥机构的功能满足设计要求。
3) 优化计算方法具有稳定、收敛快等特点,ADAMS仿真结果表明计算模型的正确性,研究结果为工程样机的改进提供了重要依据。
