三角翼飞行器滚转运动随机响应与控制
2019-06-26张永芳蒋贵荣
张永芳, 蒋贵荣
(桂林电子科技大学 数学与计算科学学院,广西 桂林 541004)
三角翼飞机(delta-wingairplane)是机翼前缘后掠、后缘基本平直、半翼俯视平面形状为三角形的飞行器。三角翼机型有着广泛的应用,如歼-8、米格-21、苏-15歼击机的平尾式三角翼飞机,“幻影”Ⅲ型歼击机和“协和”式超音速客机等的无平尾式三角翼飞机。对于战斗机而言,三角翼可以加强结构和气动稳定性,从而提高生存率。
当飞机的攻角超过临界角造成失速时,控制系统的累计误差和外部环境等都会造成飞机失去平稳,而飞机的横向运动会导致其失去平衡性与稳定性。飞机的稳定性是指在飞行中受外力干扰后不需要操作人员的干预,靠自身特性恢复原来状态的能力。飞行器在飞行的过程中,往往电路系统、自动控制系统等内部因素会受到随机干扰或风力、湿度、气压等外部因素影响飞行器的平稳性,所以在分析飞行器滚转运动时,应该考虑这些随机因素。
Elzebda等[1]对细长三角翼的亚音速机翼滚转现象的3种模型进行了数值模拟,给出了修正后的运动方程的渐近逼近解,但未讨论系统加入随机的情况。Kori等[2]提出了一种基于扩展状态观测器(ESO)技术方法,对细长三角翼的滚转运动进行鲁棒控制,Chavatzopoulos等[3]利用不完整的神经网络(PNN)来识别三角翼飞机的滚转运动,他们所讨论的是未考虑随机因素的确定性方程。Luo等[4]利用Beecham-Titchener的平均方法,得到了滚转运动抑制的最优控制输入。陈永亮[5]提出非线性动力学特性分析与控制律设计的一体化设计思想,应用于飞机大迎角飞行时机翼摇晃抑制,揭示机翼摇晃的全局运动特性,但控制律过于复杂,并且抑制结果是在理想状态下得出的。李春涛等[6]设计以滚转角速率为内回路的滚转角控制律,应用鲁棒伺服LQR优化方法,得到滚转角控制律参数,验证以滚转角速率为主控变量的控制器具有抗干扰能力,但其控制律过于复杂。杨利红[7]对飞行器纵向、横侧向通道和速度通道进行控制仿真设计,得到相对简单的滚转角控制律,但无实例分析。徐孝诚等[8]用MSC/NASTRAN软件对再入飞行器复杂结构轴向随机振动试验和横向随机振动试验进行了响应分析,吴卫国等[9]对飞机起落架动力学模型进行求解与响应分析,但他们都未对三角翼飞行器滚转运动随机响应进行分析。
为此,考虑随机因素的三角翼飞行器滚转运动单自由度系统的随机响应与控制问题,分析其稳定性。
1 飞行器滚转运动模型
对于三角翼飞机单自由度滚转运动,滚转运动方程为
(1)
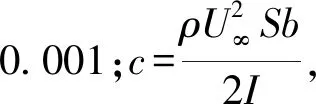
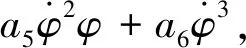
(2)
将式(2)代入系统(1),得
(3)
其中ω2=-ca1,μ1=ca2-D,b1=ca3,μ2=ca4,b2=ca5,μ3=c6a,ai(i=1,2,,6)是关于迎角α的函数,参数值由表1给出。

表1 系统(3)中的参数
2 随机响应分析
考虑高斯白噪声下三角翼飞行器滚转运动,其运动方程为

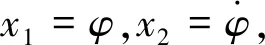
(4)
其中W(t)为谱密度为K的高斯白噪声。
随机系统(4)的恢复力u(φ)=ω2φ-b1φ3,其为非线性恢复力。由于幅值包线随机平均要求系统的恢复力是线性的,系统(4)不能用幅值包线随机平均方法讨论随机响应和稳定性。采用极坐标方法[10]处理系统(4),考虑极坐标变换:
x1=rcosθ,x2=rsinθ,
得到

b1r3sinθcos3θ+μ2r3sin2θcos2θ+
b2r3sin3θcosθ+μ3r3sin4θ+
rsin2θW(t)=f1(r,θ)+g1W(t),
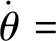
b1r3cos4θ+μ2r3sinθcos3θ+
b2r3sin2θcos2θ+μ3r3sin3θcosθ-
sin2θ+sinθcosθW(t)=f2(r,θ)+g2W(t),
幅值r(t)与相位θ(t)构成一个矢量马尔可夫扩散过程。应用随机时间平均法,上式中的fi与gi(i=1,2)是以2π为周期的时间t的周期函数,可在一个周期上进行时间平均,
高斯白噪声激励下系统的漂移系数m(r)、扩散系数σ(r)为:
σ2(r)=2πK(〈g1g1〉t+〈g1g2〉t)。
其中:
则
(5)
(6)
由于平均后的幅值r(t)方程不含θ(t),光滑后的幅值r(t)为马尔可夫扩散过程,受伊藤方程支配,
(7)
其中B(t)为单位维纳过程,系统(7)为一维伊藤方程。幅值r(t)的平稳概率密度为
其中常数C为归一化系数。
系统(7)对应的线性方程为
(8)
令Y(t)=lnr(t),用伊藤微分规则得到Y(t)的伊藤方程,
方程的解为
(9)
根据李雅普诺夫指数定义,可得到系统(9)的李雅普诺夫指数为
当λ>0,μ1/2+πK/4>0时,随机微分方程(7)对应的线性方程的平凡解局部不稳定,因此随机系统(4)在平衡点(0,0)处局部不稳定。
定理1假设下列条件成立:
其中μ1>0,谱密度K为非负,则随机系统(4)在平衡点(0,0)处局部不稳定。
由表1知,当飞行器的迎角α>19.5°,μ1>0,因而λ>0,则随机系统(4)在平衡点(0,0)处局部不稳定。随着时间t的增加,飞行器滚转运动将无法保持稳定。
3 滚转运动的控制
在无人操作的情况下,飞行器自身调节达到平稳状态,这就需要在飞行器上加入滚转角的控制器。首先飞行器通过测量装置测出实际滚转角度,然后将所测信息传输给控制器,接着控制器对接收测量信息进行处理,当滚转角大于期望角度范围时,控制器将控制信号传输给副翼舵机系统,最后接到指令的副翼舵机系统调节副翼状态,达到减小滚转角的目的。采用的控制律为
其中:Kp为滚转角传感器信号;Kd为滚转角速率传感器信号;φh期望滚转角。图1为控制滚转角的流程图,其中eh为期望信号偏差,eh=φh-φ。

图1 滚转角控制流程图
在飞行器横向运动不稳定的状态下,加入控制律得到

(10)
采用改进随机平均方法[11],求系统(10)的一维幅值伊藤方程。
系统(10)的无阻尼自由振动为
(11)

g(φ)=ω2φ-b1φ3-Kpφ,
(12)
(13)
(14)
(15)
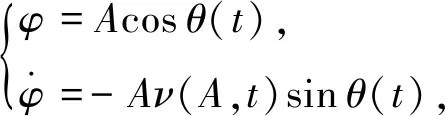
(16)
其中ν(A,t)为系统瞬时频率。将方程(16)代入方程(14)可得
其中A为系统位移的幅值。将方程(16)代入方程(15),得到总能量EH,
幅值A与总能量EH的关系为
G(A)=G(-A)=EH。
通过能量平衡法获得系统的平均频率ω(A),代替该瞬时频率ν(A,t)。当θ(t)=0时,
(17)
将平均频率ω(A)代替瞬时频率ν(A,t)代入方程(16),然后将所得结果代入方程(15),得到相关Hamilton系数EH,θ=ωt。因此,可得到残余项
R(t)=EH,θ=ωt-EH,θ=0,
(18)
考虑方程(16)是系统(10)的一个近似解,所以R不可能总为0值。
当ωt=π/4时,
(19)
方程(19)与式(17)相减,得到余项式
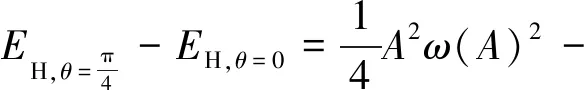
(20)
考虑输入总能量与输出总能量近似相等,令
(21)
将方程(17)、(19)、(20)代入方程(21)进行求解,可得到其等效的平均频率ω(A),
将其代替瞬时频率ν(A,t),得到近似方程解
θ(t)=ω(A)t+φ(t),
其中φ(t)为相位。
通过对系统(10)的完全转换化解,可以得到如下方程:
其中:

μ2A3ω(A)2sin2θcos2θ-
b2A3ω(A)3sin3θcosθ+μ3A3ω(A)4sin4θ+
Kpφrω(A)sinθ+KdAω(A)2sin2θ],
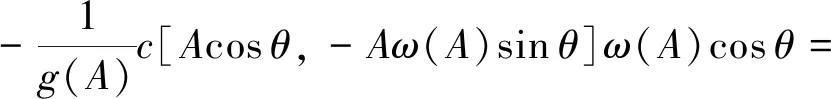
μ2A3ω(A)2sinθcos3θ-
b2A3ω(A)3sin2θcos2θ+
μ3A3ω(A)4sin3θcosθ+Kpφrω(A)cosθ+
KdAω(A)2sinθcosθ],


实施控制后的幅值伊藤方程为
dA=m(A)dt+σ(A)dB(t),
(22)
其中漂移系数m(A)与扩散系数σ(A)为:

系统(22)的平稳概率密度为
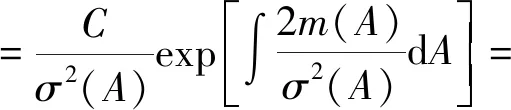
[4(ω2-Kp)-3b1A2]δ1Aδ2
其中:

系统(22)对应的线性方程为
(23)
令Y(t)=ln[A(t)],利用伊藤微分规则得到Y(t)的伊藤方程:
则其解为

根据李雅普诺夫指数定义,可得到系统(15)的李雅普诺夫指数
当λ<0,Kd>μ1+πK/2时,随机微分方程(7)对应的线性方程的平凡解局部稳定,因此,随机系统(4)在平衡点(0,0)处局部稳定。
定理2假设下列条件成立:
其中μ1为正值,谱密度K为非负,Kd为远大于μ1的正值,则随机系统(4)在平衡点(0,0)处局部稳定。
当α>19.5°时,有μ1>0,当Kd>μ1+πK/2时,系统(10)的李雅普诺夫指数
则随机系统(10)在平衡点(0,0)处局部稳定,飞行器在受到随机干扰的情况下,通过控制器的调节,飞行器的滚转运动由原来的不稳定状态变为稳定状态。
4 结束语
利用随机微分方程,建立具有速度参激的三角翼飞行器滚转运动模型,采用极坐标法、时间平均法与伊藤微分规则将随机系统化为一维伊藤方程,得到系统的平稳概率密度和随机系统不稳定的充分条件。建立加入控制律的滚转运动新模型,采用改进时间平均法与伊藤微分规则,将系统化为一维伊藤方程,得到系统稳定的充分条件,为三角翼飞行器滚转运动的控制提供理论依据。在此条件下,对于系统可能出现的分岔行为,有待进一步研究。
