水库坝址区防渗帷幕措施方案优化分析

艾尼瓦尔·牙生

（新疆水利水电工程建设监理中心，新疆 乌鲁木齐 830000）

0 引言

水库修建过程中，坝趾区防渗设计是一项复杂的工程。由于缺少既定的规范，拟从形态出发，使用防渗帷幕长度、防渗帷幕宽度、防渗帷幕深度作为防渗帷幕设计参数。数值模拟是目前工程设计中一种常用的方法，但由于其模型建立较为复杂，往往需要花费大量的时间。因此，提出使用代理模型代替数值模拟分析。代理模型目前在可靠性优化设计[1]、机械结构设计[2-3]等方面有较多的使用。粒子群算法是一种优化算法，可以快速获取全局最优值，目前在无人机航程规划[4]、围岩参数敏感性研究[5]、合金性能[6]、机械故障诊断[7～8]等方面已经取得了较多的研究成果。

1 代理模型法—粒子群算法防渗帷幕优化设计模型基本原理

1.1 模型原理

使用KRIGING 代理模型进行计算，1951 年Krige 首次提出KRIGING 法，并最早在矿产分布预测评价中应用[9]。20 世纪80 年代后期在结构优化设计中开始应用KRIGING 法。KRIGING 计算方法如下式：

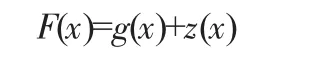
式中：g（x）表示回归部分，为自变量x 的多项式；z（x）表示随机变化过程。

z（x）满足以下统计规律：

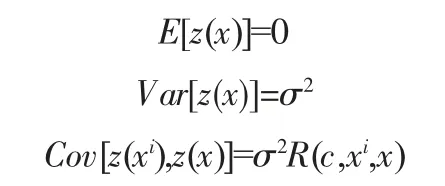
式中：R（c，xi，x）表示以C 为相似系数的相关函数，通常以高斯函数作为相关函数。

式中：di表示待预测评价的点xi与样本选取点之间的距离。

根据z（x）的统计特征可得：

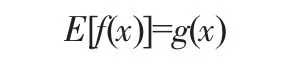
使用各样本点的响应值线性加权叠加插值计算待预测评价点xi的响应值。

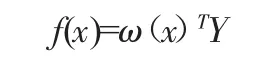
式中：ω（x）表示待求权系数。

通过整理可得KRIGING 法的模型表达式：

1.2 代理模型精度检验

使用代理模型进行计算时，要求代理模型必须具备相应的计算精度，这样才能获取精度较高、结果可靠的计算结果。一般使用最大误差和均方根误差来对代理模型的精度进行检验：

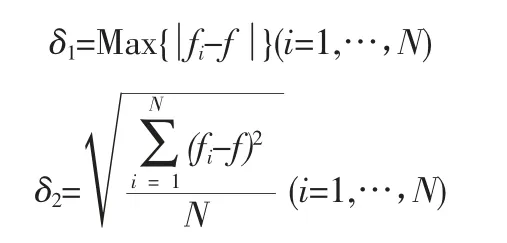
式中：δ1、δ2分别代表最大误差和均方根误差；N 代表精度检测点个数；i 表示第i 个精度检测点。δ1、δ2的值越小表示代理模型精度越高。

2 防渗帷幕优化设计模型建立

以新疆某重力坝坝趾区防渗帷幕优化设计为例进行研究。该重力坝长为50 m，高为20 m，顶宽4 m，底宽20 m 主要承担防洪、蓄水的作用。防渗帷幕与坝趾区，主要承受坝体压力和上下游水压力以及防渗帷幕自身的重力。坝体、坝基、防渗帷幕材料参数见表1。

表1 各处材料强度参数

2.1 样本点选取

使用拉丁超立方方法选取的样本点在空间范围内分布均匀，具有代表整个空间的特点同时也可以达到快速计算收敛的特点。当计算变量的个数为K 时，样本点的选取应当大于（K+1）（K+2）/2 个。在确定重力坝防渗帷幕参数、水头高度等因素之后，选取防渗帷幕的长（X1）、深（X2）、厚（X3）三个因素作为计算变量进行防渗帷幕优化设计。结合拉丁超立方方法，为了计算精确度，共选取35 个样本点建立代理模型，选取15 个计算模型作为精度检验数据。

2.2 基于防渗帷幕长度、防渗帷幕宽度以及防渗帷幕深度的代理模型构建

使用ANSYS 软件进行防渗帷幕优化设计的数值模拟，该软件在各行业内均有使用。首先建立ANSYS 计算模型，使用MATLAB 获取ANSYS 的计算结果，获取样本点的渗透稳定性和渗流量以及防渗帷幕长、深、厚的变化量。根据上述的代理模型建立方法，建立计算模型，并对所建立的代理模型进行精度检验，计算精度检验结果见表2。

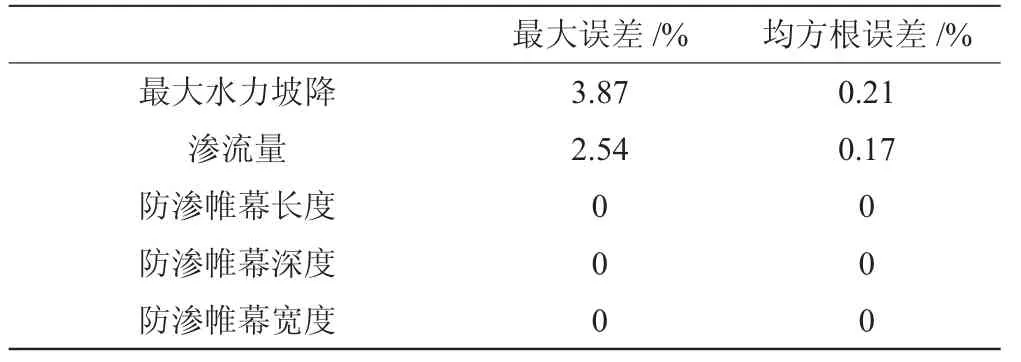
表2 代理计算模型精度评价

通过表2 可以得知，所建立的代理模型最大水力坡降的最大误差为3.87%、均方根误差为0.21%；渗流量最大误差为2.54%、均方根误差为0.17%。所建立的代理模型精度较高，可以满足工程中防渗帷幕的设计要求。因此，使用最大水力坡降、渗流量、防渗帷幕长度、防渗帷幕宽度、防渗帷幕厚度，作为代理模型代替ANSYS 有限元数值模拟分析结果是可靠的。

3 基于改进粒子群算法模型参数优化

加入交叉因子、学习因子和动态惯性因子克服粒子群算法的局限性（局部最优值和早熟收敛）。

3.1 交叉因子

交叉因子的引入可以获取粒子所对应的测量位置Xi,t=1，将测量位置Xi,t=1与该粒子的最优位置以离散的方式进行交叉计算，从而生成测试位置交叉计算的公式如下：

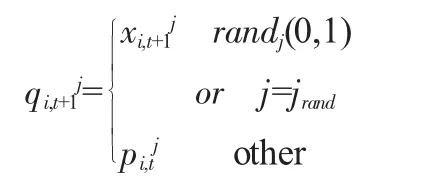
式中：randj(0,1)表示一个在[0,1]范围内符合均匀随机分布的一个数；jrand表示[1,D]范围内的一个随机整数；p 表示交叉的概率。

计算完成后对粒子的历史最优位置进行更新，更新结果如下：

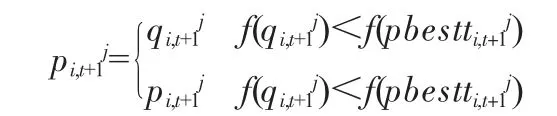
3.2 学习因子和动态惯性因子

在粒子群算法进行迭代计算的过程中，惯性权重按照线性规律进行衰减，当遇到复杂问题、非线性问题时则不可以以简单的线性衰减来进行计算[10]。因此，提出动态惯性因子对基本粒子群算法进行改进。进行惯性动态因子计算时，首先需要定义粒子进化度和粒子聚合度两个概念。

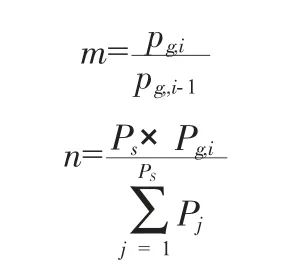
式中：m 表示粒子进化度；n 表示粒子聚合度；Pg,i、pg,,i-1分别表示当前全局最优值和上一次计算时的历史全局最优值；Ps表示粒子群的规模。

粒子进化度为粒子改变状态的直接反应，在计算开始时，粒子进化度是一个相对较小的值，表明粒子以较快的速度进行进化。惯性权重是一个与粒子进化度和粒子聚合度密切相关的参数，计算方法如下：

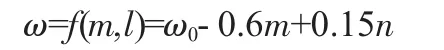
式中：ω0表示初始惯性权重。

使用粒子进化度和粒子聚合度对惯性权重进行优化设计，可以提高粒子群基本算法的稳定性。

学习因子表示粒子的学习能力。引入两个学习因子C1、C2。算法计算初期，需要对一个大范围内进行全局搜索，从而可以保证粒子的多样性，此时C1较大、C2较小。在计算后期为了计算的准确性需要减小C1、增大C2，从而保证计算的精度。

4 防渗帷幕优化设计

4.1 设计变量的选取

设计变量采用向量的形式表示，Z=[X1,X2,X3]，各参数意义如下：防渗帷幕长度（X1）、防渗帷幕宽度（X2）、防渗帷幕深度（X3）。

4.2 变量约束条件

Z1=[68,5,12]；Z2=[120,20,38]；I≤1.8；Q≤15 L/s。其中，Z1、Z2分别表示各变量的下限和上限；I 为代理模型中的最大水力坡降；Q 为代理模型中的最大渗流量。

4.3 目标函数建立

设计目标函数时需要引入惩罚函数，惩罚函数的引入可以加快运算速率提高计算精度。建立新的目标函数如下：

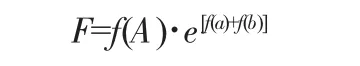
式中：f(a)、f(b)为惩罚函数；为建立的新的目标函数。

4.4 防渗帷幕优化设计结果

使用改进粒子群算法基于KRIGING 法的模型，使用计算机进行迭代计算，获取防渗帷幕最优设计方案，设计变量值初始和优化结果见表3。

表3 结构设计优化前后各变量参数

如表3 所示，优化后的防渗帷幕最大水力坡降降低为1.354，渗流量为13.5 L/s。防渗帷幕混凝土方量大规模降低，经济效益和工程防渗效果均满足要求。

5 结论

1）使用代理模型代替防渗帷幕设计过程中的有限元数值模拟计算，通过精度检验模型精度较高，满足设计要求。

2）使用改进的粒子群算法，建立的代理模型进行计算，获取设计变量的最优值。优化后的防渗帷幕大大降低了混凝土使用方量，并取得了较好的防渗效果。