乌鲁瓦提水库综合利用优化调度方案分析

王 涛

（乌鲁瓦提水利枢纽工程建设管理局，新疆 和田 848000）

0 引言

水资源是我国国民经济赖以生存和发展的基础，水资源短缺成为了近年来制约国内经济发展的重要因素之一[1～2]。尤其在我国北方区域，气候干燥，夏季因降雨较多而导致洪水灾害，冬季则因雨水较少而造成干旱，形成了我国水资源在时间和空间上不平衡的现象，水资源利用率较低[3]。水库的兴建可在一定程度上缓解水资源的季节不均衡性，在汛期，水库会严格的控制水库水位，在枯水期水库也可及时提供所需的水量，即为水资源调度[4]。在水资源调度中，水库起着非常重要的作用，如果水资源调度合理，不仅能保证大坝安全，而且能够通过水库的调蓄作用满足各用水部门的要求[5～6]。随着对水库调度要求的提高，原有的水库常规调度已无法满足兴利需要，水库优化调度已成为了国内水资源优化利用方面的研究热点。

目前水库调度主要分为常规调度和优化调度两大类。Yazigil H 等[7]以绿河流域为研究区域，采用线性规划法计算水库实时防洪调度模型并建立了调度系统，指出优化调度较常规调度结果更为合理；肖敬等[8]以位于北方的水库为研究对象，基于改进的POA 算法对水库调度过程进行了优化，并比较了POA 算法和改进POA 算法的计算结果，指出改进POA 算法的收敛速度更快，计算效率更高，且水库下泄流量更小；赵同心[9]在研究决策支持理论的基础上开发了水库防洪调度决策系统，有利于充分发挥水库的综合效益，张春波等[10]建立了碧流河水库防洪调度决策系统，为水库优化调度的研究打下了基础。

乌鲁瓦提水库位于新疆和田地区和田河西支流喀拉喀什河中游，为该流域唯一的水利枢纽工程，直接关系到当地灌溉、发电、防洪等方面的发展，做好水库的调度工作尤为重要[11]。本文基于最大削峰模型、最小洪灾损失模型2 种模型，主要通过改进粒子群算法提出水库优化调度方案，并综合比较了常规调度、粒子群算法及改进粒子群算法，得出最优方案。

1 模型构建

1.1 最大削峰模型

最大削峰模型是通过尽可能减小进入水库的洪峰流量来保障水库下游的安全，最大削峰模型的目标函数为：

式中：q(t)为第t 时段下泄流量；q'(t)是区间洪水；t0、tT为水库泄流过程的开始时间和结束时间；T 为调度的总时段数。

1.2 最小洪灾损失模型

在水库防洪调度过程中，以洪灾害损失最小为目标的防洪调度模型为最小洪灾损失模型，目标函数如下：

式中：C 是洪灾损失系数；Qt为成灾流量；Δt 为蓄水量变化所需时间。

1.3 约束条件

(1)水量平衡方程约束

式中：Vt+1为t+1 时段蓄水量；It为t 时段水库的平均入库流量；Qt为水库t 时段内的平均下泄流量；Δt 为蓄水变化量的时间；Vt为t 时段蓄水量。

(2)水库水位约束

式中：Zmin调度的最低水位即死水位，Zt为t 时刻的调度水位，Zmax为水库调度过程中的最高水位。

(3)水库下游防洪安全约束

式中：Qt为t 时段水库泄量，Qan为下游防洪的安全泄量。

2 改进粒子群算法模型求解

传统的粒子群算法粒子群算法虽在一定空间内的寻优能力较强，但该算法局部搜索能力较差，易陷入局部最优。本文基于混沌理论，采用Logistic 映射来生成混沌变量，迭代方程如下：

式中：μ 是控制参数，当μ=4，0＜x＜1 时映射处于完全混沌状态。

基于公式（7）将混沌变量转化为优化变量：

式中：a、b 为优化变量y 的取值区间上、下限。在搜索过程中，混沌变量在[0,1]上搜索寻优，与其对应的变量则在相应的问题研究域内寻优。

改进粒子群算法求解过程如下：

（1）随机生成一个D 维的向量x1=（x11,x12,……,x1D），依据logistic 映射回归方程，将式（6）改写成：

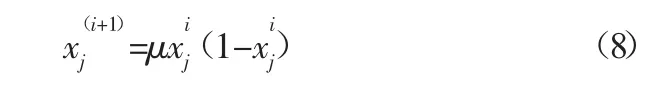
式中：μ=4；Zj为混沌变量，0≤xj≤1；i 表示粒子群序号，i=1,2,……,N-1；j 表示混沌变量的序号，j=1,2,……,N；取混沌迭代次数为0，对公式（8）赋予D 个具有微小差异的初值，得到D 个混沌变量x，取i=1,2,……,m，得到。

（2）由适应度函数计算初始化的m 个粒子的适应度值，将个体适应度最优的粒子的位置记为Pbest，群体中适应度最优的粒子位置记为gbest。

（3）由改进权重的粒子群更新公式对粒子进行更新。再次计算粒子的适应度值，并重新更新最优值。

（4）判断是否满足终止条件。如果满足，算法终止否则，执行步骤（4）。

（5）结果输出gbest。

3 计算结果分析

3.1 不同方法水库调度结果

表1～表3 为基于常规调度方法、粒子群算法和改进粒子群算法下的水库调度结果。由表中可以看出，3 种方法对水库百年一遇洪水的调度结果中，入库流量最大值均为1617.66 m3/s，最大下泄流量3 种方法分别为560.32 m3/s、559.86 m3/s 和559.37 m3/s，总下泄流量改进粒子群算法较常规调度法降低了8.73 m3/s。

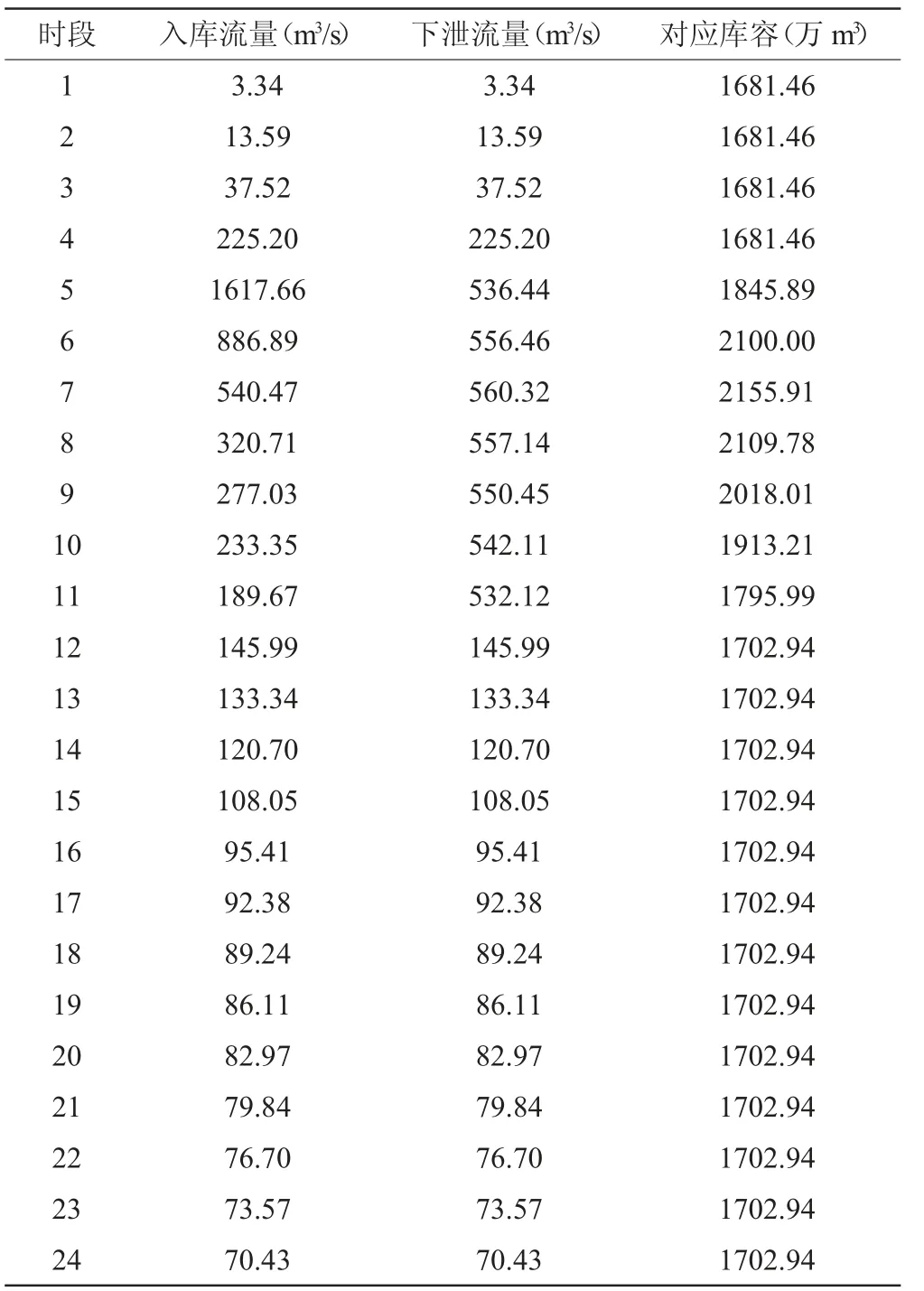
表1 常规调度结果

表2 粒子群算法调度结果

表3 改进粒子群算法调度结果

3.2 不同方法计算对比

对百年一遇洪水分别采用常规调度、粒子群算法和改进粒子群算法进行计算，结果见表4。由表4 可以看出，三种方法得到的最高水位均低于百年一遇洪水水位，均符合水库要求，同时改进粒子群算法下泄流量平方和最低，表明该算法的优化效果最好。

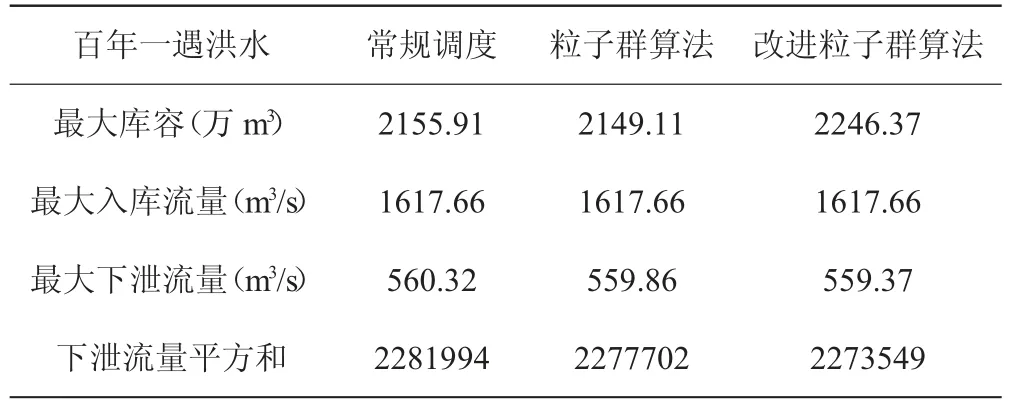
表4 三种方法计算结果对比

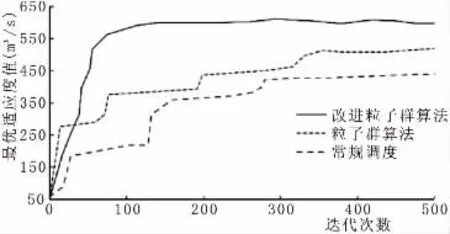
图1 不同方法收敛速度对比

取迭代次数为100 次时，3 种方法在不同月份的水位计算情况，结果见图2。图2 显示，改进粒子群算法较其他算法变化更加稳定，不会出现上下浮动的现象，表明该方法较其余方法具备一定的优越性。

图2 不同方法水平计算结果图

4 结语

通过改进粒子群算法的计算，比较该算法与常规调度、粒子群算法的结果，证明其优越性，该方法收敛性明显高于其余方法，且计算结果的整体稳定性较高。在现如今智能计算的普遍应用环境下，改进粒子群算法可作为一种标准算法，应用于水库优化调度中。