几种处理模糊图像复原技术的方法

徐 梅 张显强＊

（贵州警察学院实验中心，贵州 贵阳 550002 ）

随着日新月异的智能化和大数据技术发展，图像复原技术承载着先进性供于军事、测控中心、医学成像和公安侦查等领域使用。随着全国平安城市建设的推进，摄像头24 h不间断监控已经成为对重点防控区域进行监控的技术手段。目前，诸多单位、公共场所均已安装摄像头和监控录像系统以便实时检测，例如：政府机关、银行、公安、军事基地、收费站、商场、超市、工厂、居民小区等，它们利用自身优势对日常发生事件及社会人的行为进行实时观察、记录、特殊事件下对特定场所、特定人员的音频、视频信息进行处理。监控录像对保障人民利益和监督公共安全方面责无旁贷，尤其是记录了大量犯罪分子作案的现场视频、痕迹以及其他有用信息。然而，监控在获取图像的过程中，由于监控位置安装不当、光学系统散焦背景下光线太暗或太亮、监控与景物之间的相对运动、存储介质的局部损坏以及传感器硬件设备性能的局限性等多种因素，使得视频图像的质量退化现象无法规避，造成图像模糊不清。不能为城市视频监控系统质量评估提供依据支撑，也不能为侦查破案提供有价值的线索。在一定条件下，通过图像处理技术（图像去雾、图像去噪、图像复原等）对监控录像带中的模糊图像（或退化图像）进行处理，可获得可辨认的人像或车牌号码等较清晰的图像信息，从而使视频图像的质量评价分数得以提高，为公安机关破案提供正确的侦查方向和范围，提高破案效率。

图像退化过程中有效高频信息的缺失是导致图像模糊的成因。这些高频信息正是体现图像细节的关键所在，图像复原与图像退化互为逆过程，图像复原即是找回缺失的高频信息，这种复原技术过程是对图像退化的过程进行分析，依据退化原因建立图像退化模型，采取精准的复原技术算法复原成尽可能清晰的高质量图像。由于方法的误差性，各种算法过程大都是近似的，一般用某些最佳准则来作为约束，其基本理论是解析延拓理论[1]和正则化理论[2]。根据采集者的需求，将退化后图像的各个部分进行复原可以得到许多有用的信息[3]。例如在刑事侦查中，犯罪嫌疑人的模糊行为可以通过图像复原的方法进行恢复等，因此研究图像视频的清晰度复原具有重要的技术价值和现实意义。文章主要针对模糊图像的复原方法原理进行研究，在对图像去噪、图像复原、图像去雾等算法进行分析，介绍小波阈值去噪声法、维纳滤波复原法、正则化复原法、图像去雾算法等方法的关键技术。

1 小波阈值去噪声法

近年来，小波理论以优良的时频特性及实际应用广泛等特点而受到去噪领域中研究者的青睐和重视。基于小波变换Donoho提出了小波阈值去噪理论[4-5]。其中，软硬阈值去噪方法因具有较强的实际应用及优良的运算性能效果，其方法备受各界人士关注。基于小波阈值去噪算法的主要思想是：基于二维图像构造含噪公式，如式（1）所示，在考虑图像去噪的基础上结合阈值思想，将这个阈值作为临界点分离含噪成分。

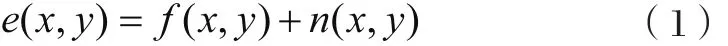
其中，无噪图像表示为f(x, y)，非高斯噪声表示为n(x, y)，均值为零，方差为σ[6]。去噪过程主要分为五个步骤完成，第一步，由离散小波变换对e(x, y)=f(x, y)+n(x, y)含噪图像进行处理，得到有用信息的小波系数和噪声对应的小波系数。第二步，经过小波分解，得到高频幅值大的有用信号小波系数和低频幅值小的噪声小波系数，此时设定一个合适的阈值λ。第三步，过渡到分尺度阈值去噪阶段，以阈值λ为分界点，将小于、大于阈值的分解系数分离开。第四步，对分离结果进行处理，舍弃小于阈值λ部分由噪声引起的分解系数，保留经筛选程序大于阈值λ的分解系数（硬阈值方法）；对阈值λ小于或是等于分解系数绝对值的值做平移收缩处理（软阈值方法），最后一步是用处理后的小波系数进行重构信号，即可重构去噪图像，以此为依据完成对图像的高效去噪。其基本流程图如图1所示。

图1 小波阈值去噪流程图

硬阈值函数：

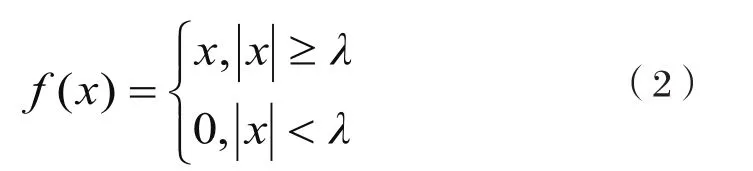
软阈值函数：

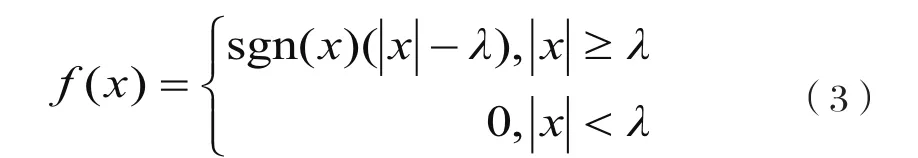
其中，sgn(x)为符号函数。在阈值的确定上，Donoho首先提出了通用的阈值为其中，σ为噪声标准方差，M代表了图像像素的行，N代表了图像像素的列，如何选取阈值的范围，噪声的标准方差和信号的长度是复原图像的关键。

影响小波降噪效果的因素很多，但阈值函数和阈值的选取对实现小波阈值去噪具有决定性作用，是其核心因素。虽然软、硬阈值函数对图像去噪效果较好，但也存在硬阈值函数不连续的缺陷，软阈值函数相较于硬阈值函数虽然连续，若出现某个阈值小于系数时，恒定偏差就会产生，这一结果的产生会导致了图像变得光滑，而未能显现出较多细节，不利于图像的去噪。

2 维纳滤波复原法

维纳滤波复原法和逆滤波复原算法两者均建立在图像退化这个基础上，且前者是在后者的基础上改进而得。因此，下面简单对图像退化机制和逆滤波复原算法进行介绍。

图像模糊、降质、失真、含噪等现象普遍存在于图像退化过程中，影响了图像的清晰度，要得到尽可能清晰的图像，了解图像退化的机制和构建降质图像相应的数学模型成为至关重要的因素。为了使数学模型得以简化，通常将图像的降质过程看作一个线性不变的过程。设原始图像函数f(x,y)经过一个系统函数H(x, y)作用后，与噪声函数n(x, y)相加，形成退化后的图像函数g(x, y)，即可得到实际的图像，这一过程用数学表达式为：所以，图像退化的一般模型可如图2表示。

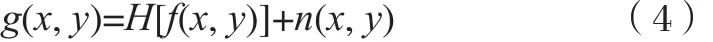
如果把公式（4）写成卷积形式则可以用公式（5）表示：

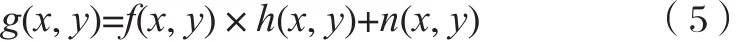
无噪声时，又可表示为

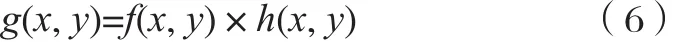
图像逆滤波复原算法是一种较简单、使用最早的无约束复原方法[7]。此算法是基于傅立叶变换中的卷积定理，对模型做傅立叶变换处理，得到式（7）的表达式。

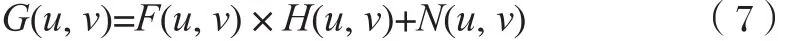
式中：F(u, v)—未失真图像；H(u, v)—退化模型；G(u, v)—退化图像；N(u, v)—含噪声的离散傅立叶变换。

寻找传输函数为H(u, v)的⁀滤 波 器成为维纳滤波方法的核心步骤，它使复原出的图像(x ,y)与原始图像f(x, y)的均方误差达到最小，如公式（8）所示：

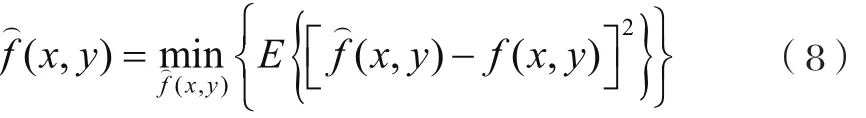
采用维纳滤波恢复得到的最佳估计，由公式（9）给出：

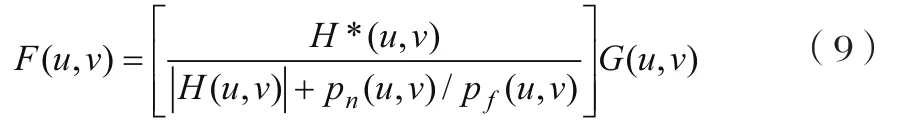
其中，式中[]—维纳滤波器；H*(u,v)—H(u, v)的共轭序列；pn(u, v)—噪声图像的功率谱；pf(u, v)—未降质图像的功率谱，两者的比值为归一化的计算提供条件。客观上，很难估计pn(u, v)和pf(u, v)，因此，通常用下式来近似维纳波复原[8-9]：

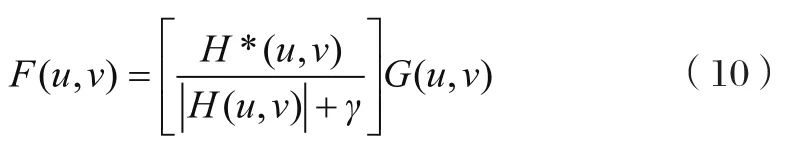
式中：γ—常数，在数值上取Lagrange乘子λ的倒数。

基于最小均方误差为准则的维纳滤波方法，解决图像的噪声方面有较好的效果，但也存在不足之处。其在视觉效果方面不满足人眼视觉特性。人眼对诸如暗处和高梯度等地的误差敏感度会大大下降；此外大部分图像实际是非平稳的随机过程，使用维纳滤波复原的前提条件较难实现。

3 正则化复原法

从图2的图像退化模型可知，图像退化模型中或多或少存在不同程度的噪声因素，在整个求解清晰图像的过程中可能存在以下三种情况：

（1）无解。当出现噪声引入在采集视频图像中，此时由于噪声大、成分复杂会导致复原图像严重畸变，这样就无法求解出原始清晰图像。

（2）非唯一解。在一个图像序列中，高频信息往往能够体现诸多相似特性的细节，且序列图像之间存在着空间和时间连续性，某一特定特征对应了特定的高频细节信息，如果此对应的高频细节信息缺失；最终可能会出现多个解的现象，对应的也能求解出多个原始图像。

（3）非连续解。出现此种情况主要是噪声和 PSF（点扩散函数）对成像过程中有一定的影响。PSF在成像过程中扮演了有限冲激响应滤波器的角色，对盲复原来说，提高解卷积恢复出的原始图像质量通常依赖于PSF准确性的估计，因此，PSF估计的准确性对整个图像的复原效果是决定因素之一。而噪声一般分布在高频信号中，若高频部分出现稍小的噪声扰动、PSF的估计不准确、出现偏差都会导致图像突发性及较大幅度的改变，图像的严重畸变成为一个不可避免的结果，这样就很可能存在非连续解。

超图像复原过程中通常发生这种不适定的求逆问题[10]。正则化方法[11-12]成为解决此类问题的首选方法。其主要思想步骤是从式（4）中得到g、H与n的相关知识，再求原图像的近似解，它是利用图像的先验知识等约束对解空间，从而创造约束条件，其优化解可以由式（5）转变而得，即：

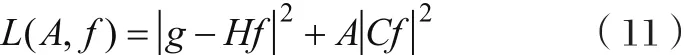
4 图像去雾算法

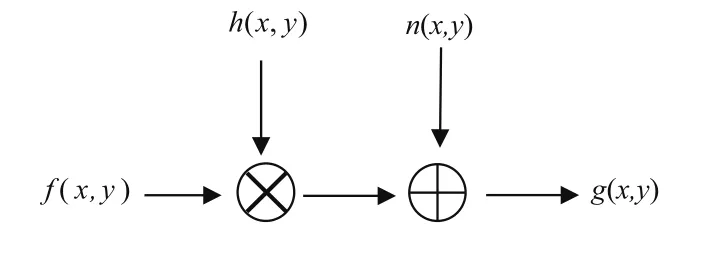
图2 图像退化模型图

在雾天环境下，拍摄到的图像视频具有雾杂质，为获得去雾清晰图片，追根溯源是要对造成图像退化的物理机理深入了解。雾天条件下大气中会悬浮过多的小微粒，在光系统的作用下这些小微粒发生散射效应。散射现象的主要表现是使物体表面反射光减少，相应地也会引起观测到的光强度降低，即随着传播距离越远，传播过程中有各类介质阻碍光沿原来的路径传播，偏离原路径使光强度随之削弱。同时，基于光源特性雾周边环境的大气光也对这些粒子有散射作用，经试验证明这种光强度与传播距离成反比关系[13]。所以上述情况最终导致雾天拍摄图像视觉效果不好，如对比度低、颜色暗淡等特征有明显的退化。1975年，Mc Cartney根据著名的Mie散射理论提出了新的大气散射模型[14]，此模型的应用率较高，已普及到计算机视觉及图像处理领域。

在计算机图像处理学中，雾天图像的退化模型采用式（12）来描述：

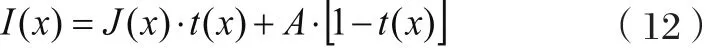
其中，I(x)=(I(x), I(x), I(x))T— 实际得到的雾天图像；

rgbJ(x)=(Jr(x), Jg(x), Jb(x))T—无雾图像，A—大气光估计值；t(x)表示透射率。

雾天图像复原算法的成功与否取决于能否准确估计出透射率t(x)和大气光值A。对式（11）进行变换得可得到退化前的图像。该算法首先输入雾天图像得到暗原色图像，通过Levin的soft抠图方法[15]计算得到拉普拉斯矩阵L，以暗原色图像为基础可粗略估计出大气光值A和透射率t(x)。将拉普拉斯矩阵与透射率t(x)共同作用，可计算求得稀疏线性系统得到精细化的透射率图t ′(x)。将所得到大气光值A和精细化透射率t ′(x)结合求解出无雾图像J(x)，根据雾天图像的退化模型实现对雾天图像的复原。其流程图如图3所示。

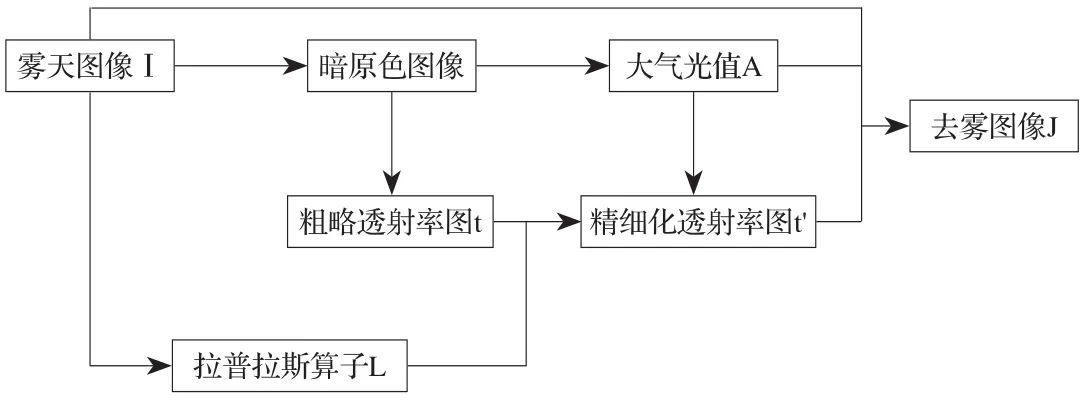
图3 去雾算法流程图

基于暗原色先验的图像去雾法是一种对图像景物要求较高的去雾算法，满足暗原色先验特征的图像还原效果较理想，图像中出现天空或者白色物体的景象，会产生一定误差的大气光值和透射率估计，因此还原图像的效果较不理想 。

5 结语

通过以上对四种图像复原技术算法的介绍，正则化复原方法是诸多经典复原算法中使用率较多的算法，它的解能够更好地趋近清晰图像的解，使复原过程中存在的病态问题得以解决，其应用更加普遍。以上四种复原技术都能很好地对图像进行复原。然而任何一种单一的复原技术都不是获得图像清晰的最佳方法，因此，目前大多数的研究人员利用复原技术的优缺点将多种方法结合还原图像的清晰度，以期为研究图像模糊复原技术在各行各业中的应用专家和学者提供理论参考依据。