奇妙的翻折

江苏省无锡市蠡园中学九（7）班 孙悦纹

手工课上，我拿出纸张，对折，再对折，折成一架飞机。我打开纸飞机，左右两边是一样的，心想这不是数学中的翻折嘛！在数学学习中，翻折问题很常见，有时只需用些常规方法，问题便可迎刃而解。

考题再现如图1，矩形OABC的边OA、OC分别在x轴、y轴上，点B在第一象限，点D在边BC上，且∠AOD=30°，四边形OA′B′D与四边形OABD关于直线OD对称（点A′和A，B′和B分别对应）。若AB=1，反比例函数k≠0）的图像恰好经过点A′、B，则k的值为 ____ 。

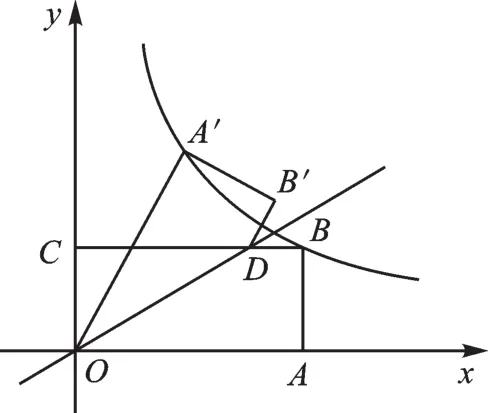
图1

初看这个题目，也许会被难住。题中没有告知任一点的坐标，虽然给出了一条边的长度（AB=1）和一个特殊角度（∠AOD=30°）。这些条件会让我想到含30°、60°角的直角三角形。但30°角与长度为1的边不在同一个三角形内，难以建立关联。

进一步分析，题中告知四边形OA′B′D与四边形OABD是对称的。言下之意就是，四边形OA′B′D是由四边形OABD沿OD翻折而得到，根据“重合的量相等”可以得到∠A′OD=∠AOD=30°，A′B′=AB=1，OA′=OA=BC，于是∠A′OA=60°。所以，若连接AA′，则△OAA′为等边三角形。但进一步思考后可发现，连接AA′对解题并没有帮助。对于60°角，我们还能想到什么呢？三边长之比为1∶2的直角三角形！如图2，过点A′作A′E⊥AO交x轴于点E。设OE=a，则A′E=，OA′=2a，所以A′（a，B（2a，1）。把 A、B 两点的坐标代入k≠0），可 得

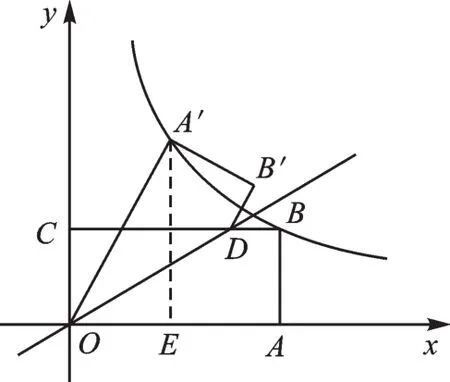
图2

几经波折，问题终于解决了。我想，在学习数学时，要抓住关键，看透本质，理解条件背后要提供的真正条件；对特殊角度、长度要敏感，把握正确方向，来添加合适的辅助线；不要被带入“思维定势”的误区。此外，关于翻折问题，变换前后组合在一起的图形看似复杂，但其实也给出了许多有用的信息——重合的量均相等。这正是翻折的奇妙所在，也是找到解题思路的灵丹妙药。

教师点评

无论尝试构造等边三角形还是构造含30°角的直角三角形，其本质都是将翻折问题转化为我们熟悉的特殊三角形问题。小作者从生活中的折纸入手，经历了两种不同的构造方法，虽然不一定都行得通，但仔细体会，两种构造方法都在“情理”之中。解题不需要死记硬背，唯有结合具体的情境才能找到更合适的方法！