几何变换的“奥秘”
2019-06-26江苏省无锡市蠡园中学九
江苏省无锡市蠡园中学九(7)班 于 点
上周五的午间,我和几位好朋友正围坐在一起“吹牛”。突然,我同桌冲了进来,手里挥着几张纸,兴冲冲地对我们说:“来,看看这道中考题!”于是,我们的话题与注意力马上转移到试题上。
考题再现如图1,已知∠MON=120°,点A、B分别在OM、ON上,且OA=OB=a,将射线OM绕点O逆时针旋转得到OM′,旋转角为α(0°<α<120°且α≠60°),作点A关于直线OM′的对称点C,画直线BC交OM′于点D,连接AC、AD,有下列结论:①AD=CD;②∠ACD的大小随着α的变化而变化;③当α=30°时,四边形OADC为菱形;④△ACD面积的最大值为。其中,正确的是____。

图1
显然,根据对称性,我们可以知道OM′是AC的垂直平分线,所以AD=CD。哈哈,结论①太简单了!
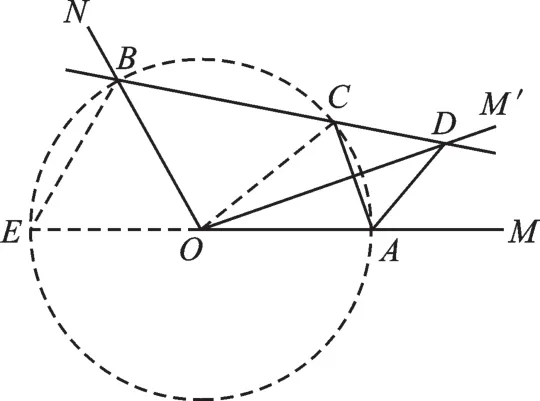
图2
再看结论②。角度?旋转?我的脑海中闪出一个字——圆。不管了,试试再说。如图2,我以O为圆心,OA长为半径作⊙O,根据“圆的内接四边形对角互补”可得∠ACB=180°-∠E=180°-60°=120°,所以∠ACD=60°。所以结论②是错误的。
做完一半的题目,我松了一口气,心想前面的两题不难,但是后面的应该不会这么简单吧。于是,我又埋头苦干了。当α=30°时,∠COD=∠AOD=30°,又因为OC=OA,所以△AOC是等边三角形。另一方面,由于DC=DA,∠ACD=60°,所以△ACD也是等边三角形。故OC=OA=AC=AD=CD,因此,四边形OADC为菱形。所以结论③也正确。
做完前三问,我有些沾沾自喜,看向同桌,她却淡定地说:“别急,还有一个结论呢!”我一看,不就是求最大面积嘛。由于△ACD是等边三角形,所以只要边长取得最大值,面积就相应地取得最大值。在图2中,AC是☉O的一条弦,如果最大,只要是直径就可以了。接下来就看看能否取得这种情形即可:由于∠AOC=2α,所以当α=90°时,∠AOC=180°,此时,AC即为直径。接下来就可求得△ACD的面积=,化简结果为所以④也正确。
这道关于几何变换(旋转、翻折)的题目,其奥秘就在于变换前后重合的量相等,虽只是填空,但解题时也需小题大做。对于一些常见题型,我们要有一些基本的应对策略。如果遇到一些特殊角度,我们在解题时也要学会联想相关的特殊性质。
教师点评
选正确结论的问题一直是难点,小作者从旋转、对称的基本性质入手,层层递进,引入“圆”并最终解决该图形变换问题。同学们仔细体会,角在圆中变为“圆周角,圆心角”,线段在圆中变为“弦、直径”,从而可以发现不变的量及变换的量的最值,是不是收获很大?
