瞄准不变量 巧解中考题

严 芹

图形的变换问题一般集众多知识点于一题，解决方法往往也比较多。近年来，它已成为中考命题的一大热点。有些同学在遇到此类题型时，会产生一定的畏惧心理，但是，如果从图形的变换特点出发，在变换中瞄准不变量，就能找到突破口，巧解中考题。下面，笔者以近几年的中考试题为例进行剖析，希望对同学们有所帮助。

一、平移变换

例1（2017·江苏无锡）在如图的正方形方格纸中，每个小的四边形都是相同的正方形，A、B、C、D都在格点处，AB与CD相交于O，则tan∠BOD的值等于_____。

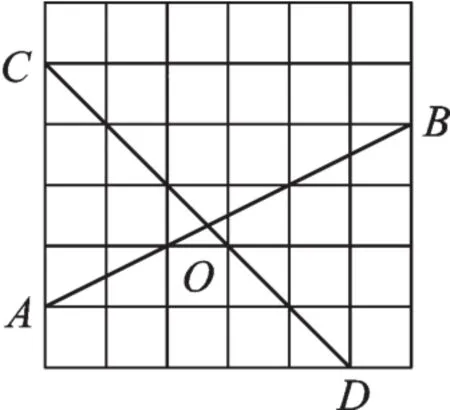
图1

【解析】点O为非网格点，如果直接作垂线构造直角三角形，那么在求解线段长度时会比较繁杂，有一定的难度。如果我们将CD平移到合适的位置，使得它与AB的交点恰好为格点，再根据平移的性质——两直线平行，同位角相等，则可较为简捷地求解问题。

解：如图2，平移CD到C′D′，交AB于格点O′，则∠BO′D′=∠BOD，tan∠BO′D′=tan∠BOD。

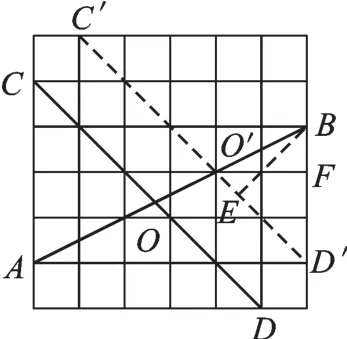
图2

过点B作BE⊥O′D′于点E，设每个小正方形的边长为1，则BD′=3，O′F=2，O′D′=22。

利用等积法，得：

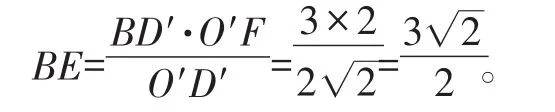
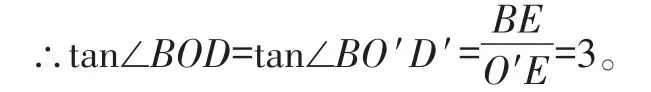
【点评】本题在表述中没有直接出现与“平移”相关的词语，而是需要同学们通过分析、思考，借助平移的手段，利用平移的性质，将结果中的角（∠BOD）转换成以格点为顶点的方便计算的角。这样一来，问题就变得简单多了。

二、翻折变换

例2（2016·江苏淮安）如图3，在Rt△ABC中，∠C=90°，AC=6，BC=8，点F在边AC上，并且CF=2，点E为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是_____。

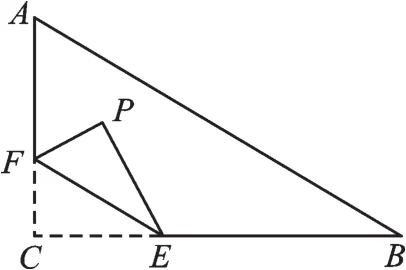
图3

【解析】由翻折得FP=FC=2，所以点P到F的距离为定长2，故点P在以F为圆心、2为半径的圆上。显然，当FP⊥AB时，点P到AB的距离最小。

解：由翻折知FP=FC=2，点P在以F为圆心、2为半径的圆上。故当FP⊥AB时，点P到AB的距离最小。

由勾股定理得AB=10。

当FP⊥AB时，延长FP交AB于点M（如图4）。

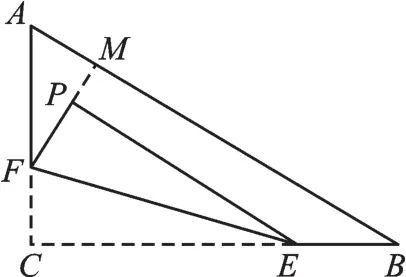
图4

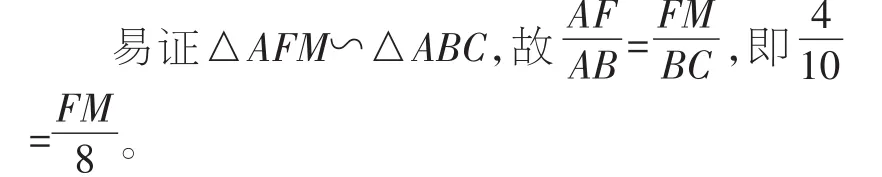
解得FM=3.2。

∴PM=FM-FP=3.2-2=1.2。

∴点P到边AB距离的最小值是1.2。

【点评】翻折变换中，折叠前后重合的量相等，即对应边、对应角相等。在翻折过程中，点P的位置、点P到AB的距离都在变化，但是FP的长度始终等于2，且点F是定点，抓住这些不变量，再依据“垂线段最短”便可突破难点。

三、旋转变换

例3（2017·江苏苏州）如图5，在矩形ABCD中，将∠ABC绕点A按逆时针方向旋转一定角度后，BC的对应边B′C′交CD边于点G。连接BB′、CC′，若AD=7，CG=4，AB′=B′G，则结果保留根号）。

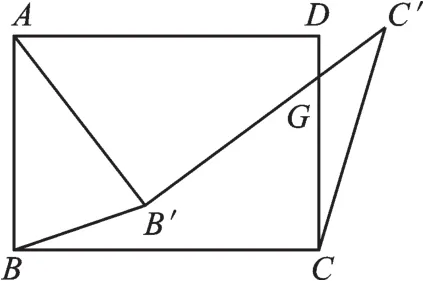
图5

【解析】由旋转知AB′=AB，AC′=AC，若连接AC、AC′，则∠CAC′=∠BAB′。由此可构造相似三角形△ABB′∽△ACC′，根据相似三角形的性质可得。若能求出AB的长，则问题得解。

解：连接AC、AG、AC′，如图6所示。

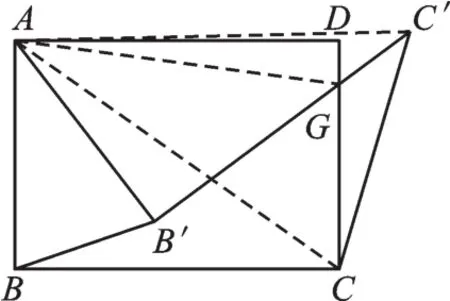
图6

由旋转知 AB′=AB，AC′=AC，∠CAC′=∠BAB′。

∵AB′=B′G，∠AB′G=∠ABC=90°，

∴△AB′G是等腰直角三角形。

在Rt△ADG中，由勾股定理得AD2+DG2=AG2，即72+（x-4）2=（

解得x1=5，x2=-13（舍去）。

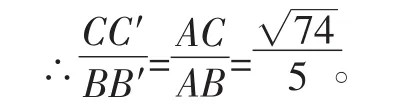
【点评】在解决本题时，同学们应抓住旋转过程中的不变量，如AB′=AB，AC′=AC，∠CAC′=∠BAB′等。同时，如果仔细观察图形的特征，就会发现一些基本模型，抓住这些基本模型，找出相似三角形，由相似的性质得到，最后运用方程思想求出相关线段长度，从而解决问题。